克里金算法在精密星历插值中的应用

晏新村，徐 良，周万里，李冬庆

（中国人民解放军91650 部队，广州 510320）

0 引言

在高精度GNSS数据处理中，为了保证结果的可靠性和精确性，通常使用精密卫星星历进行计算。由于实际作业时星历时间间隔都大于观测数据的采样间隔，使用时需要对精密卫星星历进行插值处理来满足计算的需求，以得到观测历元时刻所需要的卫星位置，提高精密单点定位的精度[1-4]。

常用的插值方法包括拉格朗日多项式插值法、内维尔插值法、牛顿插值法等，在进行插值时，为了达到较高的插值精度，插值时应尽可能使内插点位于插值弧段的中间，但是在实际的计算使用中，常需要两端位置高精度的精密星历，而随着插值阶数的增加，在靠近两端位置很容易出现龙格现象[5-10]。针对这一问题，本文在确保精密星历插值精度的基础上，提出利用克里金算法进行精密星历插值。

1 基于克里金算法的精密星历插值

1.1 精密卫星星历

精密卫星星历是精密单点定位的基础[11-12]。国际GNSS服务组织（IGS）生产的精密星历的事后星历精度优于5 cm。IGS是一个国际协作组织，其开放度也较高。因此，精密单点定位中通常采用IGS提供的精密星历，给出15 min等时间间隔点上的卫星坐标数据，坐标参考基准属于ITRF（国际地球参考框架）。表1为不同IGS精密星历的精度指标，它们在精度、时延和更新方面是不同的。

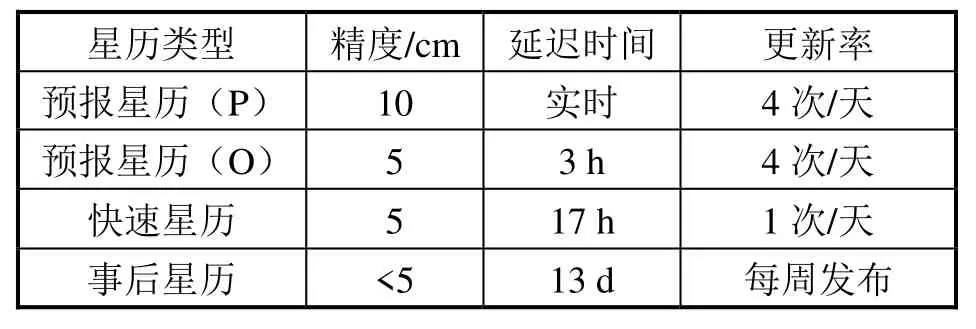
表1 不同IGS精密星历产品的精度指标

1.2 基于克里金算法的精密星历插值

克里金插值法也称空间局部估计或空间局部插值，是由地质学家克里金和统计学家西舍尔在20世纪50年代提出，并以法国科学家D.G.Krige的名字命名的一种空间自协方差最佳内插法。该方法广泛应用于地质矿产领域，是一种有效的统计分析方法[13]。

克里金插值算法利用区域化变量的原始数据和变异函数的结构特点，对未采样点的区域化变量的值进行最优、线性和无偏估计。这种方法是在分析已测样点的形状、大小、空间位置的相互关系，已测样点与待估样点的空间位置关系，以及变异函数提供的结构信息的基础上进行的。它可最大限度地利用空间取样所提供的各种信息，对待估点和已知点的位置关系，以及已知点之间的位置关系都进行了考虑。精密星历插值大多用于事后处理，不强调实时性，两段位置的插值可用前后两日的星历进行精确插值估计，研究的方法应该在星历预测或其他方面有意义，而克里金插值算法的特点正好可以提高精密星历的预测精度[14-15]。

根据克里金插值算法的基本原理，基于克里金算法的精密星历插值如下所示。

（1）首先，提取出需要插值的精密星历数据，使提取的精密星历数据是等间隔的。

（2）根据已知的精密星历坐标计算半变异函数值γ*（h）：

式中，h为滞后距，N（h）为距离为h的点对的个数，Z（xi,yi）和Z（x j,yj）分别为参考站点（xi,yi）和（x j,yj）处的插值数，对于不同的滞后距h，利用式（1）可以计算出相应的半变异函数值γ*（h）。

（3）根据半变异函数值γ*（h）拟合理论变异函数模型中的系数，具体拟合方法可参考文献[13-14]。

（4）根据拟合的理论变异函数模型构建克里金方程组，计算参与插值的各点克里金插值权重。在式中，令：

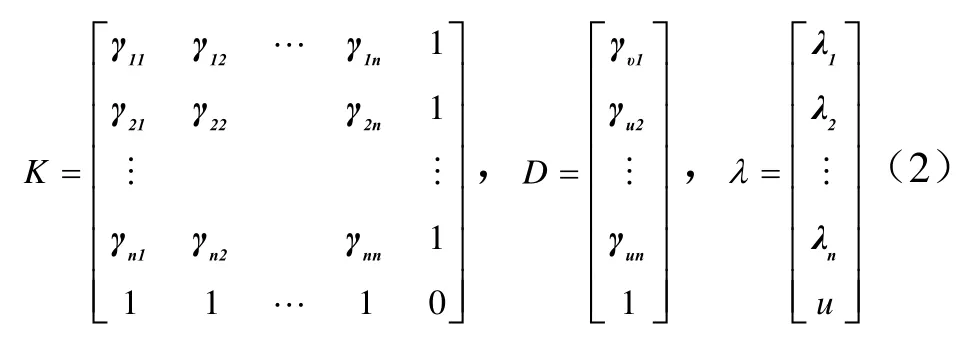
则式（2）可写为：

式中，K，D中的γij为各点间的理论变异函数值。

（5）利用克里金算法求出待插值点的精密星历数据：

2 计算分析

为了验证该方法的有效性和可行性，本文采用某日的精密星历数据，通过提取出30 min 间隔的精密星历数据，利用拉格朗日插值、内维尔插值、牛顿插值和克里金插值四种方法将其插值成15 min间隔的星历数据，再将插值结果与给出的真值数据比对，四种插值方法得到的插值误差如图1~图4所示（图中历元间隔为30 min，历元单位为个），对插值结果进行统计分析，得到结果如表2所示。

图1 拉格朗日插值结果

由图1~图4和表2可以看出，采用克里金插值方法比拉格朗日插值、内维尔插值、牛顿插值三种插值方法的插值精度更高，特别是能够有效减弱精密星历两端的插值误差，提高精密星历的插值精度。

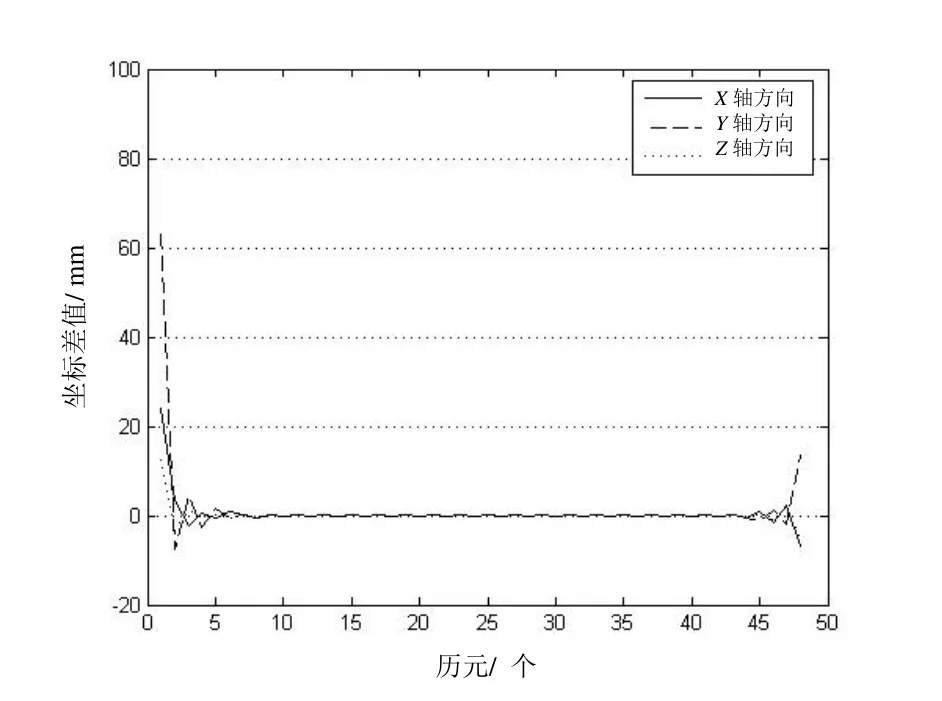
图2 内维尔插值结果

图3 牛顿插值结果

图4 克里金插值结果

表2 四种方法插值误差统计/mm

通过比较分析拉格朗日插值、内维尔插值、牛顿插值和克里金插值4 种精密星历插值方法，可以得出如下结论：

（1）相比较拉格朗日插值，内维尔插值、牛顿插值和克里金插值3 种方法可以有效地减弱和消除精密星历两端的插值误差，提高精密星历的插值精度，其中克里金插值的精度最高。

（2）相比较其它3 种插值方法，克里金插值不需要插值星历前后一段时间的星历，就能得到较高精度的精密星历插值结果。

（3）克里金插值比拉格朗日插值、内维尔插值和牛顿插值等精密星历插值方法更加考虑了精密星历的空间位置变化，因此克里金插值的结果更符合精密星历实际，插值精度也更高。

3 结论

本文将克里金算法引入到精密星历插值中，通过计算分析可知，克里金插值算法不仅考虑了精密星历插值点与已知点的相对位置，而且还考虑了精密星历各已知点之间的相对位置关系，并且克里金模型具有无偏性、最优性，在精密星历两端已知点少时插值精度比其它方法更好，能给出的精密星历插值精度更高，也能提高精密星历的预测精度，因此克里金插值算法能有效解决精密星历两端插值精度低的问题，提高精密单点定位的精度。