邻近地面建筑一体化地铁车站结构地震响应分析

韩学川， 陶连金， 安 韶， 张 宇， 史 明

(北京工业大学城市与工程安全减灾教育部重点实验室， 北京 100124)

城市轨道交通枢纽一体化结构是由地铁地下车站和地面建筑共同组成的新型结构形式，通过技术、管理等手段对地铁车站与其周边建筑进行有机组合、资源共享、紧密衔接，使得城市地下空间的利用实现集约化和高效化[1].与传统的单体车站结构相比，城市轨道交通一体化结构同时涉及地铁地下车站结构和地面结构，一体化结构空间效果显著.邻近地面建筑一体化结构具有形式复杂、空间尺度大、安全隐患不易发现且修复难度较大等特征，因此，对邻近地面一体化结构进行抗震分析，研究其破坏机理具有十分重要的意义.

目前，关于地下结构的研究主要集中在功能单一、结构形式简单的地铁车站结构[2-3]、连体并行地铁车站结构[4]以及复杂地下综合体[5-7]等.王国波等[8]基于十字换乘车站结构的三维有限元模型，讨论了不同条件下车站结构的地震特性，且将换乘站地震响应与单体车站结构进行对比，探讨了其空间效应及抗震性能.李方杰等[9]基于有限元方法，研究了相对位置上不同的地上结构对地铁地下结构地震反应的影响.王淮峰等[10]利用ANSYS有限元程序建立了一系列典型高层框架结构及地下车站的二维平面应变模型，研究了地上结构对地下结构地震动力响应的影响参数.Pitilakis等[11]研究了单个和多个相邻地表结构对地下圆形隧道地震响应的影响.郭靖[12]研究了地下结构在不同场地和不同埋深条件下对地表临近建筑产生的影响范围，发现场地土体越软弱，地铁车站所能产生的影响就越为显著.王国波等[13]建立隧道- 土体- 地表邻近框架结构相互作用体系数值计算模型，对比分析了隧道与邻近框架结构之间地震响应影响规律.

本文基于ABAQUS软件建立了地下地铁车站- 土- 地面建筑一体化结构大型三维有限元数值模型，研究了地震波不同频谱特性对邻近地面建筑一体化结构的地震响应的影响.同时，将计算结果与单体地铁车站结构进行对比分析，以期为相似工程的抗震设计提供参考依据.

1 地铁车站结构- 土- 地面建筑结构体系的有限元计算模型

以某在建邻近地面一体化结构为工程背景，基于ABAQUS软件建立邻近地面建筑一体化地铁车站三维有限元数值模型，如图1所示.其中，地铁车站为三层三跨钢筋混凝土矩形框架结构，宽22.3 m，高19.6 m，顶板厚0.5 m，中板厚0.4 m，底板厚1.0 m，侧墙厚1.0 m，中柱截面0.8 m×1.2 m，间距8.0 m.地面建筑为框架- 剪力墙结构，层高3.0 m，地上19层，中柱截面1.0 m×1.0 m，剪力墙厚0.3 m.结构主体混凝土强度采用C40，柱混凝土强度采用C50.一体化结构区域分布及尺寸如图2所示.

图1 三维有限元计算模型Fig.1 Three-dimensional finite element calculation model

图2 一体化结构区域分布及尺寸示意图(单位：cm)Fig.2 Regional distribution and dimension diagram of integrated structuresl (Unit: cm)

邻近地面建筑一体化结构三维数值模型尺寸为310 m×80 m×120 m.采用八节点减缩积分实体单元(C3D8R)模拟土体介质，结构墙和板采用减缩积分的四节点曲面壳单元(S4R)进行离散，梁和柱采用两节点空间线性梁单元B31进行离散，网格划分满足Kuhlemeyer等[14]提出的精度表达式.引入黏弹性人工边界单元[15]，把波动作用转换成人工边界节点作用力来实现波动的模拟，实现了有限元 ABAQUS软件中设置黏弹性边界条件和施加等效荷载[16].土体与地下结构之间的相互作用采用接触对的方法进行模拟，法向接触采用“硬接触”，切向接触面采用“有限滑动”，服从Coulomb摩擦定律，摩擦因数取为0.4，满足位移协调一致原则.视土体为理想弹塑性体，服从Mohr-Coulomb屈服准则，场地土层性质及力学参数，如表1所示.结构采用线弹性本构来模拟其力学行为，其物理参数详如表2所示.

表1 土层计算参数

表2 混凝土动力本构模型计算参数

选用Kobe波和Taft波的反演地震波作为基岩水平向输入地震动，总持时选取地震波振动最为明显区段的前20 s.其中，Kobe波为神户海洋气象台观测点记录的近场脉冲地震波，频带相对较窄；Taft波为加利福尼亚州观测点记录的中远场地震波，频带相对较宽.将地震波加速度峰值调整为0.2g，地震动的加速度时程曲线及傅里叶谱，如图3所示.

2 计算结果与分析

以一体化地铁车站结构为研究对象，分别从地震波类型和空间效应两方面，对一体化地铁车站结构进行地震响应分析，并将计算结果与单体车站结构进行对比，综合分析了邻近地面建筑一体化地铁车站结构的地震动力响应特性.定义地铁车站结构不同深度处的水平位移幅值与车站底部水平位移幅值的差为车站结构的相对水平位移；定义地铁车站各层顶底板水平位移幅值的差为车站的层间相对水平位移；定义影响百分比=(计算结果最大值-计算结果最小值)/计算结果最小值.

2.1 模态分析

基于大型通用有限元程序ABAQUS 软件，运用线性摄动方法并采用Lanczos特征值求解器分别计算土- 一体化结构体系、土- 单体车站结构体系、一体化结构、单体车站结构和自由场地前10阶自振频率.计算模型及自由场前10阶自振频率如表3所示.计算结构的动力特性时，将结构底部固定，上部结构水平方向的自由度释放；计算土- 结构体系的动力特性时，模型底部边界固定，两侧边界设置成水平滚轴边界，其中，一体化结构与土体介质的接触面均采用绑定约束(tie).当计算自由场地的动力特性时，模型土体底部边界固定，两侧边界设置成水平滚轴边界.模态分析时土体应采用弹性模型，这是因为线性摄动方法在求解体系自振频率时要求模型是线性的.

图3 输入地震动时程曲线及傅里叶谱Fig.3 Time-history curve and Fourier spectra of earthquake ground motions

可以看出：当场地存在结构时，土- 结构体系各阶自振频率与自由场地较为接近，结构的存在对场地土动力特性的影响较小，这是由于结构相对于土体介质所占体积较小，与同体积土层置换后体系的刚度不会有明显的改变.结构各阶自振频率相差较大，这是因为一体化结构的计算高度大于单体车站结构，结构柔度较大，自振频率相对较小.

2.2 地震波类型对一体化地铁车站结构地震响应影响分析

以一体化区域地铁车站结构为研究对象，给出了不同类型地震波作用下，一体化区域地铁车站结构的位移、内力及加速度的地震响应规律.

表3 模型前10阶自振频率

2.2.1 侧向水平位移响应分析

地下结构的破坏主要是由周围土体的变形强加于结构上造成的，因此研究地下结构的位移具有十分重要的意义.一体化地铁车站侧墙的相对水平位移沿高度变化曲线如图4所示.一体化地铁车站层间相对水平位移包络值及影响百分比如表4所示.可以看出：

1) 一体化地铁车站侧墙的相对水平位移沿高度的变化形式相同，均表现为随埋深的减小逐渐增大.侧墙相对水平位移沿高度的变化曲线不具有对称性，左摆时表现为Taft波最大，而右摆时则表现为Kobe波最大，这是由地震波峰值加速度方向不同和土- 结构的单向塑性变形累积效应所导致.

2) 一体化地铁车站结构的层间相对水平位移表现为随着埋深的减小逐渐减小，Taft波作用下地铁车站的层间相对水平位移幅值大于Kobe波，各层层间相对水平位移影响百分比分别为9.3%、20.0%、18.1%.可见，不同类型地震波能够对一体化地铁车站层间相对水平位移产生显著的影响，表现为中层和底层的影响差异较大而顶层较小.

3) Taft波作用时一体化地铁车站结构地震位移响应较明显，这是因为土- 一体化结构体系的基频为0.585 Hz，Taft波在该频率附近的能量分布明显大于Kobe波，体现了地震波频谱特性对一体化地铁车站结构相对水平位移的影响.在进行结构抗震位移验算时应选取多条具有不同频谱特性的地震波.

图4 车站边墙相对水平位移Fig.4 Relative horizontal displacement of the side wall

表4 层间相对位移包络值

2.2.2 内力响应分析

不同地震波作用下，一体化区域地铁车站各层中柱的峰值内力及影响百分比如表5所示.可以看出，Taft波作用下一体化地铁车站中柱的内力幅值明显大于Kobe波，车站中柱剪力和弯矩幅值的影响较大，影响百分比约为30%，而中柱轴力的影响百分比仅在3%以内，说明不同频谱特性的地震波对一体化地铁车站轴力的影响较小，对剪力和弯矩的影响较大，结构在进行抗震承载力验算时应选取多条具有不同频谱特性的地震波.

表5 不同地震波作用下结构中柱内力幅值

2.3 一体化地铁车站结构空间效应分析

由于地铁车站与地面建筑通过地下室一体化连接，其空间效应显著，以一体化地铁车站截面1(非一体化区域)和截面2(一体化区域)作为研究区域的代表性截面，着重分析了Kobe波作用时一体化地铁车站结构位移、内力及加速度的地震响应规律.

2.3.1 侧向水平位移响应分析

地铁车站侧墙相对水平位移沿高度的变化曲线如图5所示.

图5 层间相对水平位移Fig.5 Relative horizontal displacement between layers

可以看出，一体化地铁车站的层间相对水平位移表现为随车站埋深的增加逐渐增大，一体化区域与非一体化区域地铁车站各层层间相对水平位移的影响百分比分别为21.6%、26.7%、23.9%，说明一体化地铁车站不同区域的层间相对水平位移差异明显，一体化区域的层间相对水平位移小于非一体化区域，这主要是因为邻近地面建筑通过地下室与地铁车站连接，地下室起到了水平约束的作用，导致一体化区域层间相对水平位移变小.

2.3.2 内力响应分析

一体化地铁车站截面1与截面2各层中柱柱底的峰值内力及影响百分比如表6所示.可以看出，一体化区域车站中柱所受内力均小于非一体化区域，内力的影响百分比差异明显，主要表现为轴力的影响百分比最大，弯矩次之，剪力最小.其中，轴力的最大影响百分比为150.2%，发生在地铁车站顶层位置，这是因为一体化区域车站顶部与地下室连接，上部覆土压力小于非一体化区域，导致一体化地铁车站各区域中柱所受轴力差异显著.

表6 不同截面位置中柱内力幅值

2.3.3 加速度响应分析

一体化地铁车站顶底板的峰值加速度及影响百分比如表7所示.可以看出：一体化区域各层楼板的加速度幅值小于非一体化区域，加速度影响百分比分别为14.9%、9.8%、3.3%.其中，顶板的影响百分比最大，底板的影响百分比最小，随着埋深的减小，一体化区域与非一体化区域加速度影响百分比呈逐渐增大的趋势.

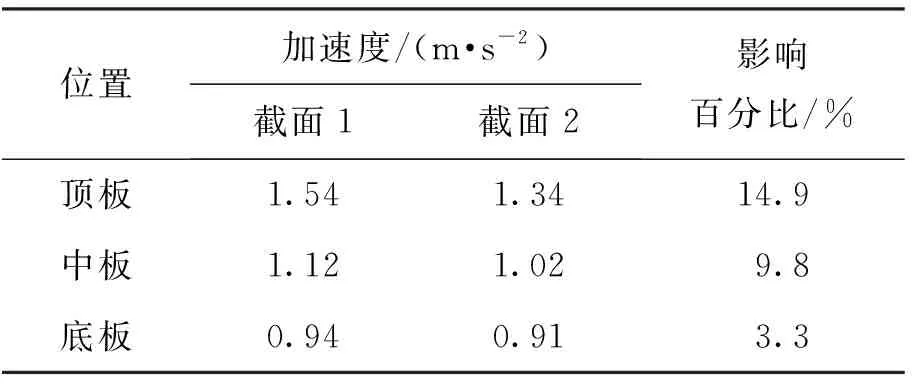
表7 结构顶板、底板峰值加速度

2.4 一体化地铁车站与单体车站地震响应对比分析

本节以一体化地铁车站截面2和单体车站为研究对象，对比了不同地震波作用时一体化地铁车站结构与单体车站结构地震响应规律的差异.

2.4.1 侧向水平位移响应分析

不同地震波作用下，2种地铁车站结构层间相对水平位移包络值及影响百分比如表8所示.可以看出：一体化地铁车站层间相对水平位移小于单体车站结构，其中，Kobe波和Taft波作用下2种车站结构层间相对水平位移的最大影响百分比分别为76.4%和71.6%，均出现在负一层，最小影响百分比分别为42.6%和29.3%，均出现在负三层，说明一体化地铁车站距地下室位置越近，车站层间相对水平位移受地面结构的影响越显著.

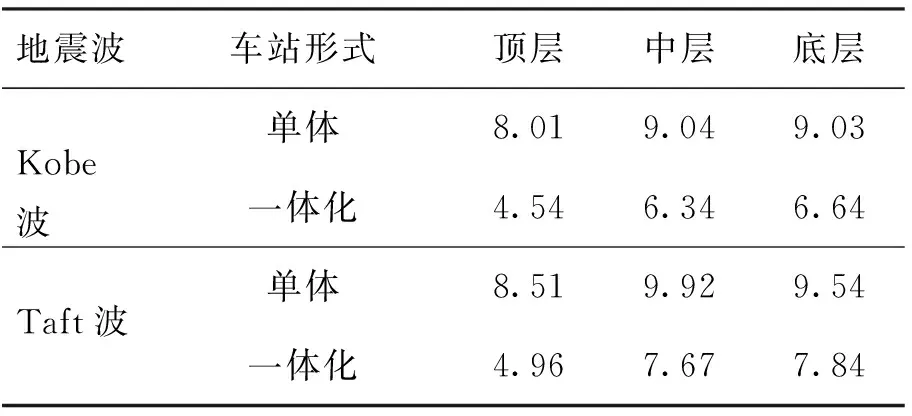
表8 层间相对位移包络值

2.4.2 加速度响应分析

不同地震波作用下，一体化地铁车站截面2和单体车站顶底板的峰值加速度及加速度影响百分比如表9所示.可以看出：一体化区域地铁车站顶底板的加速度幅值均小于单体车站结构，地铁车站中间层的加速度影响百分比最大，分别为39.2%和31.9%，地铁车站底层的加速度影响百分比最小，分别为23.1%和14.7%，其中，Kobe波对2种车站结构加速度的影响大于Taft波.

2.4.3 内力响应分析

不同地震波作用下一体化地铁车站截面2和单体车站各层中柱柱底的峰值轴力、剪力和弯矩及内力影响百分比如表10所示.可以看出：一体化区域车站结构中柱的内力幅值明显小于单体车站结构，2种车站结构内力相差悬殊，轴力的影响百分比甚至达到了300%以上；近场地震波时2种车站结构内力的差异更加明显.值得注意的是，一体化地铁车站中柱出现了扭矩，最大扭矩出现在负二层位置，而单体车站中柱是不受扭矩作用的.因此，一体化结构应进行三维地震响应分析并考虑轴力、剪力、弯矩和扭矩对中柱的共同作用.

表9 不同地震波作用下结构顶板、底板峰值加速度

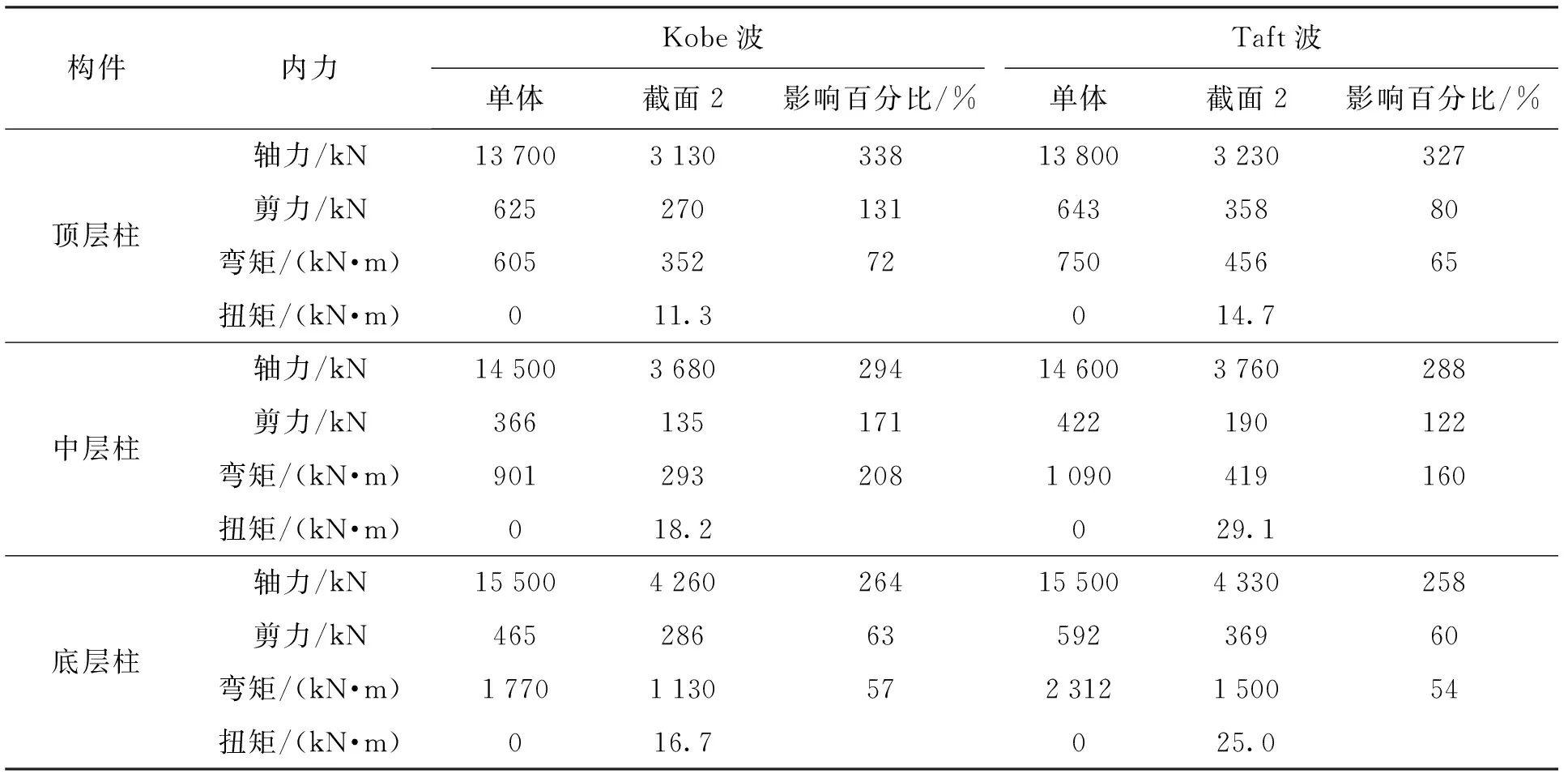
表10 不同结构类型时车站中柱内力幅值

3 结论

1) 土- 结构体系与自由场地各阶自振频率较为接近，结构的存在对场地土动力特性的影响较小，从工程的角度看可忽略不计.

2) 在土- 结构体系基频附近能量分布相对集中的地震波能够对一体化地铁车站结构的地震响应产生显著的影响，在进行车站结构抗震验算时应该选取多条具有不同频谱特性的地震波.

3) 邻近地面建筑一体化地铁车站结构具有明显的空间效应，一体化区域地铁车站结构的地震响应均小于非一体化区域，应该按照空间问题进行一体化地铁车站结构的抗震计算.

4) 邻近地面建筑一体化地铁车站结构的地震响应小于单体车站结构，近场地震波时2种车站结构的差异更明显.一体化地铁车站中柱出现了扭矩，最大扭矩出现在负二层位置，在进行一体化地铁车站结构中柱的抗震设计时，应该综合考虑轴力、剪力、弯矩和扭矩的共同作用.