锚杆受拉拔荷载渐进失效全过程与影响因素

李鹏飞， 黄靖络， 王 帆

(北京工业大学城市与工程安全减灾教育部重点实验室， 北京 100124)

锚杆凭借其施工简单、与喷混凝土配合支护效果好等优点被广泛应用于隧道工程和边坡工程支护结构设计与施工中[1].在隧道工程中，按一定间距布置的预应力锚杆能够形成承载拱结构，调动围岩自身承载能力[2-3]，控制围岩挤压大变形.通过合适的锚固技术，预应力锚杆能将预应力有效地从岩石锚杆杆体传递至岩土体.针对预应力作用下锚杆荷载传递机制与应力分布规律，国内外学者开展了大量了的室内、现场试验和轴力监测[4-12].赵同彬等[13]对全长锚固砂浆锚杆进行室内拉拔试验，研究表明拉拔状态下锚固界面剪应力分布不均匀，沿轴向呈先增后减的传递形式.沈俊等[14]通过现场拉拔试验，给出拉力型锚索灌浆体与孔壁间的剪应力分布曲线并获得剪应力沿锚固段长度的分布规律.然而，以上对预应力锚杆锚固界面应力分布规律的研究主要集中在锚杆(索)与岩土体处于弹性变形协调的受力特征，并未考虑锚固界面剪切应力- 剪切位移关系和拉拔荷载作用下全过程的力学行为.

相较于Mindlin等[15]土体位移解研究锚杆应力分布规律，黏结滑移模型能够很好地描述锚固系统受拉拔荷载作用的全过程力学行为，因此被众多学者所青睐[16-19].Yuan等[20]提出了一种用双线性局部黏结滑移模型并推导玻璃钢锚杆在拉拔荷载作用下全过程力学行为的解析解，FRP-混凝土界面一旦完成脱黏后就不存在抗剪能力，这导致在弹性- 软化- 脱黏阶段的荷载- 位移曲线是一个平坦的台阶.Ren等[21]用具有残余黏结强度的三线性黏结滑移模型描述锚固界面剪应力与剪切位移关系，得到了预测极限荷载和有效锚固长度表达式.Ma等[22]基于非线性黏结滑移模型推导了锚杆- 灌浆界面剪应力分布的表达式，剪应力的计算结果与实测数据具有较好的一致性.然而，以上已有黏结滑移模型的研究均未考虑岩石锚杆锚固界面的剪胀效应.室内和原位试验均表明在围岩中锚杆锚固界面存在剪胀作用.张传庆等[23]通过锚杆杆体- 砂浆界面直剪试验，发现剪切滑移曲线和剪胀曲线均具有明显的阶段特征.刘平[24]基于试验分析结果，考虑锚固体界面剪胀效应，提出了富水软岩地层锚固界面“弹性- 剪胀硬化- 脱黏”本构模型，将锚固界面的滑移失效过程分为弹性、剪胀硬化及脱黏3个阶段.王洪涛[25]考虑软弱围岩中的剪胀效应，提出了四线性黏结滑移模型，但其忽略了残余强度对锚固界面剪胀、软化应力区域长度的影响，这导致了荷载- 位移曲线产生“突变”的现象.Ren等[21]指出锚固界面在弹性应力区域消失之后，由于残余强度的存在，导致软化应力区域的长度发生变化.

本研究在文献[25]的基础上，考虑锚固界面进入弹性- 剪胀- 软化- 脱黏阶段之后，残余强度对剪胀和软化应力区域长度的影响，修正了剪胀- 软化- 脱黏阶段、软化- 脱黏阶段和脱黏阶段的荷载- 位移关系曲线、界面剪应力分布表达式和沿锚固长度分布的锚杆轴向应力表达式.根据2项拉拔试验研究，对四线性黏结滑移模型参数进行标定，预测锚杆在拉拔力作用下全阶段力学行为并与实测结果进行对比.讨论了锚杆半径、锚杆弹性模量和锚固长度对锚固界面剪应力分布、锚杆轴向应力和荷载- 位移曲线的影响.

1 受拉拔荷载岩石锚杆的分析模型

1.1 岩石锚杆锚固失效模式

现场原位拉拔试验中，如图1所示，岩石锚杆的锚固失效模式主要包括5种：1) 锚杆杆体断裂； 2) 灌浆材料失效； 3) 围岩破坏； 4) 锚杆- 灌浆界面失效； 5) 灌浆- 围岩界面失效[4].其中，最为常见的失效模式是锚杆- 灌浆界面失效[26].当岩石锚杆在水平拉拔荷载作用下发生锚杆- 灌浆界面脱黏失效时，其理想化的受力模型如图2所示.以锚杆锚固端点为原点建立坐标系，z代表锚固界面z处到原点的长度，τ(z)代表界面z处的剪应力，P(z)代表界面z处的轴力，dz表示锚固单元，σ表示轴向应力，下标b、g灌浆体和锚杆.另外，需要指出的是，如果锚固失效发生在灌浆体- 围岩界面，则可将锚杆与灌浆体等效为“复合锚杆”，并引入等效弹性模量，采用锚杆- 灌浆界面失效问题的分析模型来研究灌浆体- 围岩界面失效问题.

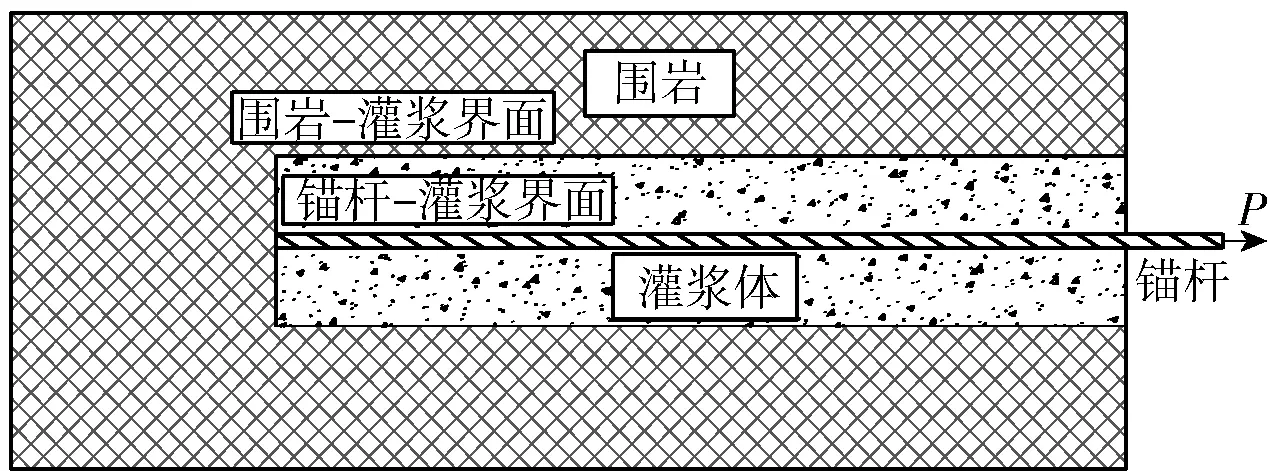
图1 岩石锚杆原位拔出试验[21]Fig.1 In-situ pullout test of rockbolts[21]

图2 锚杆- 灌浆界面失效模式的理想化受力模型Fig.2 Idealized stress model of bolt-grouting interface failure mode

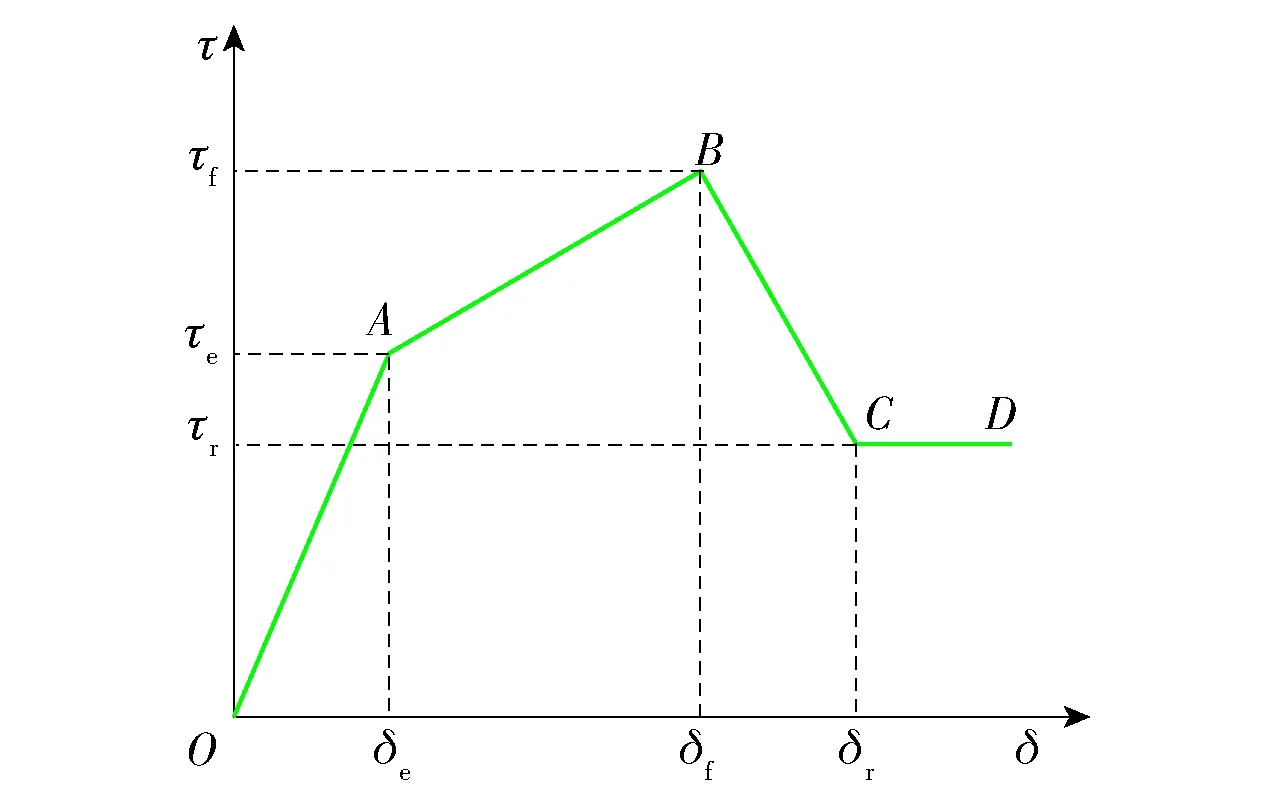
图3 四线性黏结滑移模型[25]Fig.3 Four-linear bond-slip model[25]

1.2 四线性黏结滑移模型

考虑锚杆锚固界面的滑移剪胀效应，本研究采用的四线性黏结滑移模型[25]，如图3所示.当拉拔荷载较小时，锚固界面全长处于弹性应力状态(OA段)，随着拉拔荷载的增大导致界面剪应力达到弹性应力状态的临界剪应力τe后，锚固界面将发生部分塑性滑移变形，进入塑性剪胀应力状态(AB段).当剪应力到达峰值τf之后，部分锚固界面黏结强度不断降低，进入塑性软化应力状态(BC段).水平段(CD段)用以表示完全脱黏后非零残余摩擦强度.四线性黏结滑移模型用函数表示为

(1)

式中：τ为剪应力；δ为剪切位移；下标e、f、r分别代表应力状态即将进入剪胀应力状态、软化应力状态和脱黏应力状态的临界状态.

1.3 控制方程

选取图2中锚固单元作为研究对象，根据1.1节所述假设和力平衡条件考虑建立基本方程式

(2)

假设锚杆始终保持线弹性，根据弹性胡克定律可将拉拔荷载P作用下产生的轴向位移u(z)和轴力P(z)关系

(3)

式中：a是锚杆半径；E为锚杆弹性模量.

将式(3)代入式(2)中得到灌浆锚杆控制方程表达式

(4)

剪切滑移量δ是锚杆与周围灌浆体的相对位移，假设锚固界面外的所有位移都集中在锚固界面上，则剪切位移与锚杆轴向位移相等，剪应力可以表示为与z相关的函数.

δ=u(z)

(5)

τ=τ(z)

(6)

通过确定式(1)中剪应力与剪切位移相关参数，达到求解控制方程式(4)的目的.值得注意的是，文中推导的解析解适用于全长黏结型锚杆和端部黏结型锚杆的拉拔试验，引入等效弹性模量之后同样适用于预应力锚杆锚固段受拉拔荷载作用下灌浆体- 围岩界面渐进失效全过程.

1.4 修正解析方程和全阶段力学行为分析

基于上述四线性黏结滑移模型，通过求解每个加载阶段的控制方程式(4)可以得到界面剪应力、锚杆轴向应力的分布规律和加载端的荷载- 位移响应.在拉拔荷载作用下，将锚杆荷载- 位移曲线划分为弹性阶段、弹性- 剪胀阶段、弹性- 剪胀- 软化阶段、弹性- 剪胀- 软化- 脱黏阶段、剪胀- 软化- 脱黏阶段、软化- 脱黏阶段和完全脱黏阶段7个阶段，王洪涛[25]推导了弹性阶段、弹性- 剪胀阶段、弹性- 剪胀- 软化阶段和弹性- 剪胀- 软化- 脱黏阶段加载端荷载- 位移关系和应力沿锚固长度分布的解析方程.本研究在此基础上，考虑锚固界面进入脱黏应力状态之后，残余强度作用导致剪胀区域长度L′h和软化区域长度L′s的改变，修正了剪胀- 软化- 脱黏阶段、软化脱黏阶段和完全脱黏阶段的解析方程.在拉拔荷载作用下，不同阶段剪应力的分布演化规律如图4所示，对应阶段的修正后的荷载- 位移关系曲线如图5所示.

将拉拔荷载作用下修正后的锚杆荷载- 位移力学行为分为7个阶段(见图5).点A代表荷载- 位移曲线开始进入弹性- 剪胀阶段；点B代表锚固界面开始出现塑性软化区域；点C代表加载端开始出现脱黏现象；点D代表拉拔荷载P达到极限荷载.点E代表剪应力τe达到嵌入端(见图4(h))和点F代表剪应力峰值τf达到嵌入端(见图4(i))，G点代表锚杆全长处于脱黏应力状态(见图4(j)).因此，可以将锚杆拉拔试验得到的荷载- 位移关系临界特征点代入1.4.1～1.4.4中解析方程，以确定四线性黏结滑移模型参数，并对全阶段荷载- 位移曲线进行预测.值得注意的是，图5中锚杆全阶段荷载- 位移曲线是基于理论分析得到的，无论是位移控制还是荷载控制的拉拔试验，荷载- 位移曲线出现“回缩”的现象都不能捕捉到[21].

图4 修正后剪力分布演化规律Fig.4 Distribution and evolution of shear stress after correction

图4(a)(b)为弹性阶段；图4(c)(d)为弹性- 剪胀阶段；图4(e)(f)为弹性- 剪胀- 软化阶段；图4(g)为弹性- 剪胀- 软化- 脱黏阶段；图4(h)为剪胀- 软化- 脱黏阶段；图4(i)为软化- 脱黏阶段；图4(j)(k)为脱黏阶段.Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表弹性、剪胀、软化、脱黏4种应力状态.

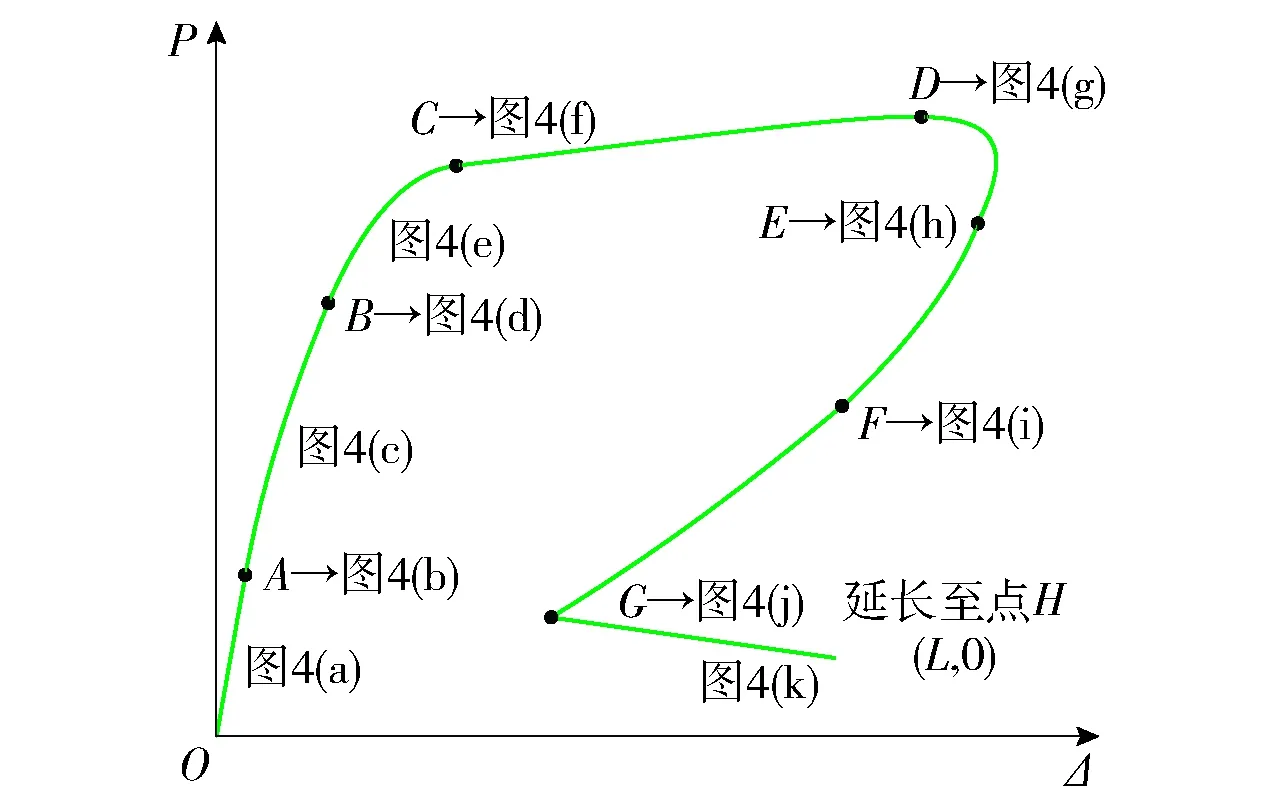
图5 修正后全阶段荷载- 位移曲线Fig.5 Load-displacement curve at all stages after correction

1.4.1 弹性、弹性- 剪胀、弹性- 剪胀- 软化、弹性- 剪胀- 软化- 脱黏4个阶段

文献[25]推导了弹性阶段(图4(a)(b)和图5中OA段)、弹性- 剪胀阶段(图4(c)(d)和图5中AB段)、弹性- 剪胀- 软化阶段(图4(e)(f)和图5中BC段)、弹性- 剪胀- 软化- 脱黏阶段(图4(g)和图5中CDE段)4个阶段的应力分布、荷载- 位移关系的解析方程.

1.4.2 剪胀- 软化- 脱黏阶段

此时边界条件为

Ph(z)|z=0=0

(7)

τh(z)|z=0=τe

(8)

(9)

(10)

us(z)|z=L-Lr=ur(z)|z=L-Lr=δr

(11)

Ps(z)|z=L-Lr=Pr(z)|z=L-Lr

(12)

界面L-Lr≤z≤L脱黏区的解析方程为

(13)

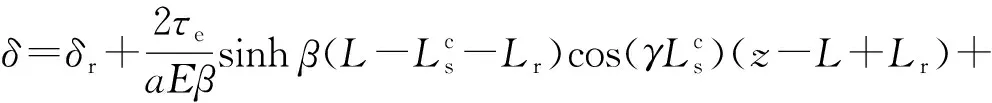
(14)

τ=τr

(15)

剪胀区和软化区的剪应力表达式为

τh=τecosh(βz)

(16)

(17)

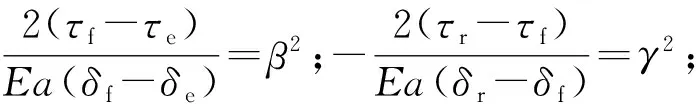
1.4.3 软化- 脱黏阶段

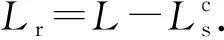
边界条件为

Ps(z)|z=0=0

(18)

τs(z)|z=0=τf

(19)

us(z)|z=L-Lr=ur(z)|z=L-Lr=δr

(20)

Ps(z)|z=L-Lr=Pr(z)|z=L-Lr

(21)

界面L-Lr≤z≤L脱黏区的解析方程为

(22)

(23)

τ=τr

(24)

将z=L代入式(22)(23)可以得到加载端荷载- 位移关系式.

1.4.4 完全脱黏阶段

锚杆- 灌浆界面软化区域长度逐渐减小为零，此时锚固界面全部处于脱黏应力状态(Ⅳ)且界面剪应力降低为残余剪应力(见图4(j)和图5中G点)，在这个阶段，锚杆承载能力完全由界面残余强度提供.将Lr=L代入式(23)可以得到软化- 脱黏阶段结束时的加载端位移

(25)

拔出位移Δ从脱黏阶段初始状态Δd一直增大到锚杆全长被拔出L，该阶段锚杆变形量相较于加载端拔出位移Δ非常小，故对该阶段锚杆自身变形量忽略不计.脱黏阶段的荷载- 位移关系可表示为

P=2πaτr(L+Δd-Δ)

(26)

式(26)表明拉拔荷载随加载端位移线性减小到零(如图5中分段GH所示).由于锚杆完全脱黏阶段的位移值L远远大于非完全脱黏阶段锚杆加载端位移，故点H不能在图中绘制.

1.5 控制参数校准

2 理论解析与试验结果对比

对2个锚杆拉拔试验的四线性黏结滑移模型参数进行校核，并将理论预测锚杆拉拔荷载- 位移曲线和沿锚杆全长轴向应力分布与实测数据进行对比.同时，不同岩土体与灌浆体中岩石锚杆的拉拔试验可以对四线性黏结滑移模型待定参数进行校核，并间接反映岩土体及灌浆体的力学性能对岩石锚杆受拉拔荷载作用下渐进失效过程的重要影响.

2.1 荷载- 位移曲线

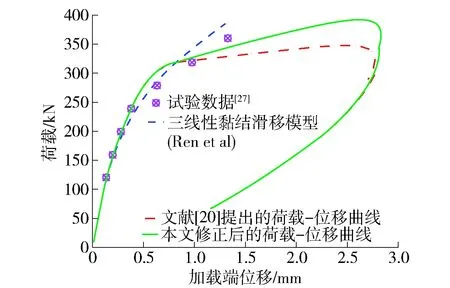
图6 预测荷载- 位移曲线与刘波等[27]试验数据对比Fig.6 Comparison between predicted load displacement curves and test data in Ref.[27]

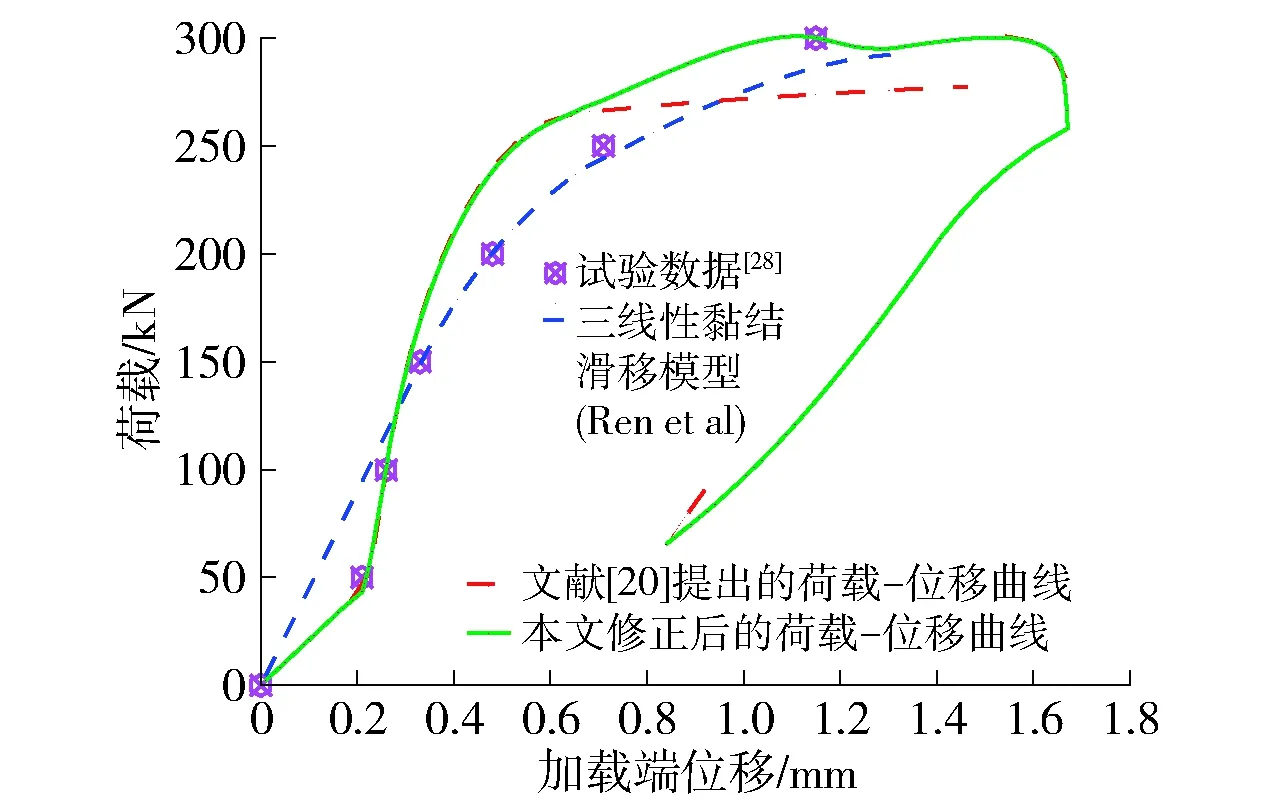
图7 预测荷载- 位移曲线与荣冠等[28]试验数据对比Fig.7 Comparison between predicted load displacement curves and test data in Ref.[28]

从以上2个算例可以看到，修正后的荷载- 位移曲线与实测数据具有良好的一致性.在刘波等[27]算例中，本文修正后的荷载- 位移曲线预测效果好于三线性黏结滑移模型所推导的荷载- 位移曲线，当锚固界面应力状态进入脱黏阶段后，三线性模型预测结果并不准确.

在荣冠等[28]算例中，本文修正后的荷载- 位移曲线在弹性阶段和弹性- 剪胀阶段拟合效果优于三线性黏结滑移模型所推导的荷载- 位移曲线，但在弹性- 剪胀- 软化阶段拟合结果有较小的偏差.

王洪涛[25]忽略了残余强度导致剪胀区长度和软化区长度的改变，推导的荷载- 位移曲线在进入剪胀- 软化- 脱黏阶段和软化- 脱黏阶段的临界状态时发生明显的间断跳跃的情况.

Ren等[21]指出残余强度的存在导致软化区域的长度发生变化.本文修正的结果解决了上述荷载- 位移曲线间断跳跃的问题.

2.2 轴向应力与剪应力分布

将荣冠等[28]室内拉拔试验校核所得到的模型参数与相关应力区域长度参数代入文献[25]相关应力解析方程，通过拉拔荷载作用下全阶段力学行为解析方程求解沿锚杆全长轴向应力和剪应力分布.荣冠等[28]虽然没有监测锚杆在拉拔荷载作用下，锚固界面剪应力实测数据，但可以通过2个监测点应变差得到界面剪应力分布关系式，计算式为

(27)

式中：εi+1为测量点i+1处的应变值；εi-1为测量点i-1处应变值；τi为测量点i处剪应力；ΔL为2个测量点的间距.

如图8、9所示，在不同加载水平下，四线性黏结滑移模型相较于三线性黏结滑移模型预测锚杆轴向应力和剪应力曲线与实测数据之间吻合更好.可以看到，在锚固界面未进入脱黏应力状态之前，锚固界面剪应力和锚杆轴向应力最大值均处于加载端，并向嵌入端逐渐减小.图8中拉拔荷载为250 kN时，锚固界面剪胀应力区域轴向应力与实测结果有一定误差，而拉拔荷载为150 kN时，整体拟合效果较好.图9中拉拔荷载为150 kN时，锚固界面剪应力分布与实测结果有较小误差，这是由于剪应力分布试验数据从轴向应力实测数据推导出来，拟合结果与实测结果存在一定误差，而拉拔荷载为250 kN时，预测结果与实测结果整体吻合效果较好.

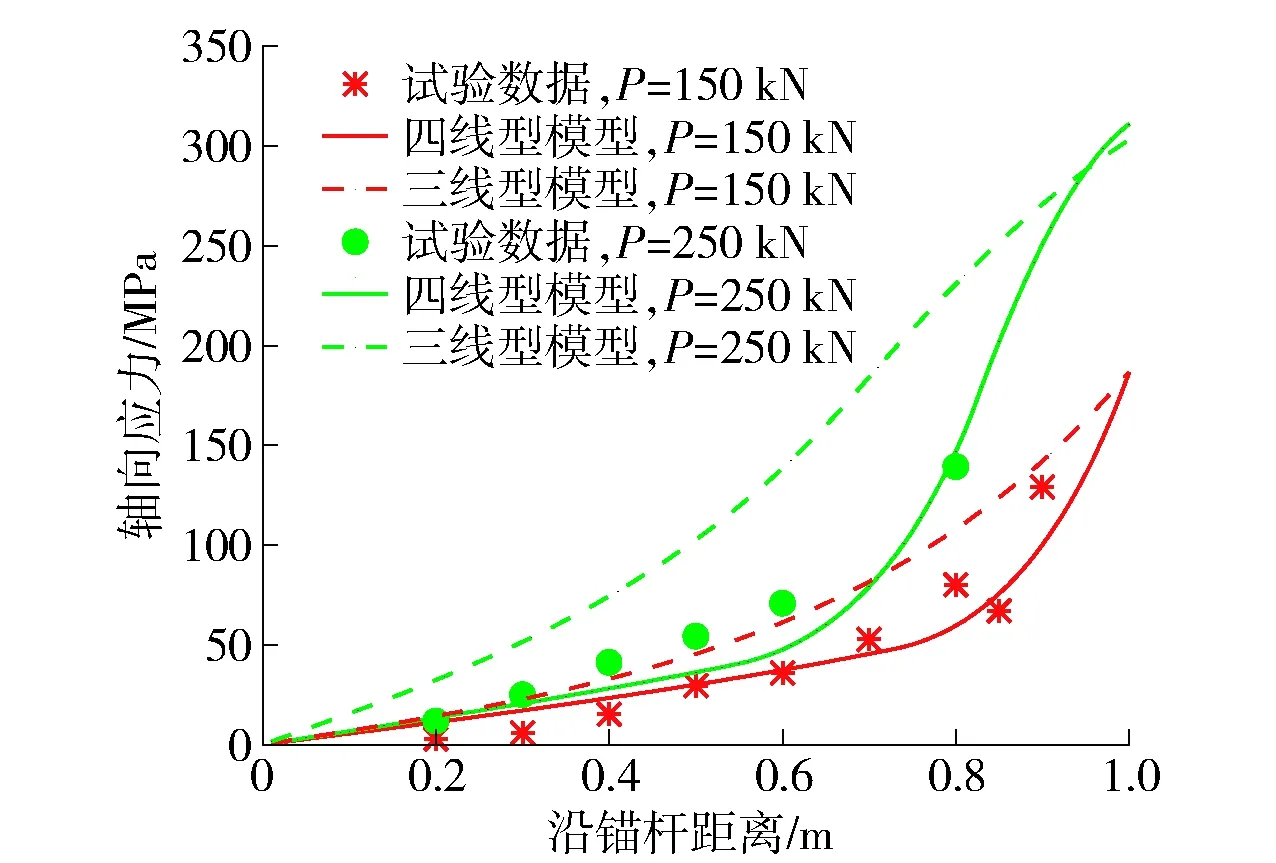
图8 预测锚杆轴向应力与荣冠等[28]试验数据对比Fig.8 Comparison between predicted axial stress of bolts and test data in Ref.[28]

图9 预测锚杆剪应力与荣冠等[28]试验数据对比Fig.9 Comparison between predicted shear stress of bolts and test data in Ref.[28]

3 参数分析

以2.1节中刘波等[27]试验给出的参数作为参考值，分析锚固长度、弹性模量和锚杆半径3个参数对荷载- 位移曲线，应力分布规律的影响.

3.1 锚固长度

不同锚固长度对锚杆荷载- 位移曲线影响如图10所示.研究结果表明，在弹性阶段、弹性- 剪胀阶段和弹性- 剪胀- 软化阶段锚杆荷载- 位移关系与锚固长度无关.在弹性- 剪胀- 软化- 脱黏阶段，脱黏区域存在恒定的残余强度τr，荷载将随着位移增大而继续增大.图11展示了加载端相同位移条件下，锚固长度对剪应力的影响.当锚固长度较小时，整个锚固范围内的承载能力得到充分发挥，随着锚固长度的增加，其界面剪应力分布将逐渐呈现不均匀的特征，锚固界面加载端剪应力已经达到残余强度，但远端剪应力仍然很小.另外，锚杆锚固长度为4 m和5 m的剪应力分布曲线已经完全重合，意味着此时整个锚固界面承载潜力的发挥程度与锚固长度无关.图12给出了加载端相同位移条件下，锚固长度对轴向应力的影响.可以看出，随着距加载端距离的增加，锚杆轴向应力衰减速度逐渐表现出不均匀性，当锚固长度增加到一定程度时，再增大锚固长度，锚杆只有加载端一定范围内承受轴向应力.

图10 锚固长度对荷载- 位移曲线影响Fig.10 Effect of the anchorage length on load-displacement curves

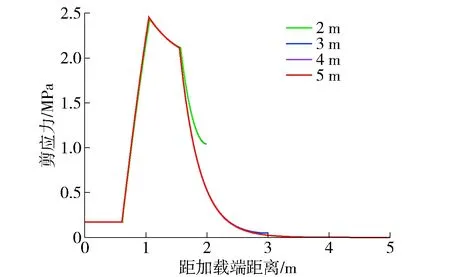
图11 锚固长度对剪应力影响Fig.11 Effect of the anchorage length on shear stress

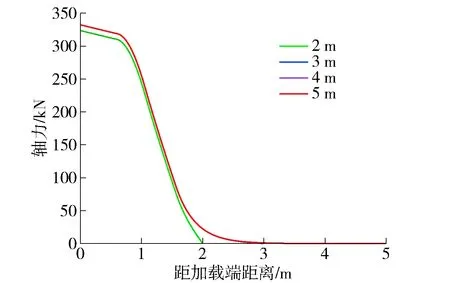
图12 锚固长度对轴向应力影响Fig.12 Effect of the anchorage length on axial stress

3.2 弹性模量

图13表示了锚杆弹性模量对荷载- 位移曲线的影响.可以看出，极限荷载随着锚杆弹性模量的增大而增大.在弹性阶段，弹性模量的增加对锚杆荷载- 位移曲线影响不大，但弹性模量的增加对于界面脱黏时的锚杆延性有较大的限制作用.图14、15给出了在弹性- 剪胀- 软化阶段加载端相同位移下，弹性模量对应力沿着锚杆全长分布规律的影响.从图14中可以看出，锚杆弹性模量越大，剪应力峰值越早地向远离加载端移动，锚杆全长越早地进入弹性- 剪胀- 软化阶段；在远离加载端的弹性区域，相同位置的剪应力随着锚杆弹性模量增大而增大，而弹性模量对剪胀区域剪应力值大小的影响程度降低.图15表明了相同位置的轴应力随着锚杆弹性模量增大而增大，弹性模量与该阶段轴应力峰值呈正相关，而对峰值剪应力和残余剪应力没有影响.

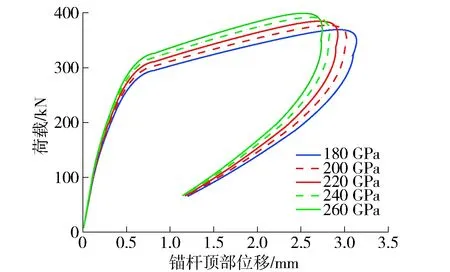
图13 锚杆弹性模量对荷载- 位移曲线的影响Fig.13 Effect of the bolt Young’s modulus on load-displacement curves

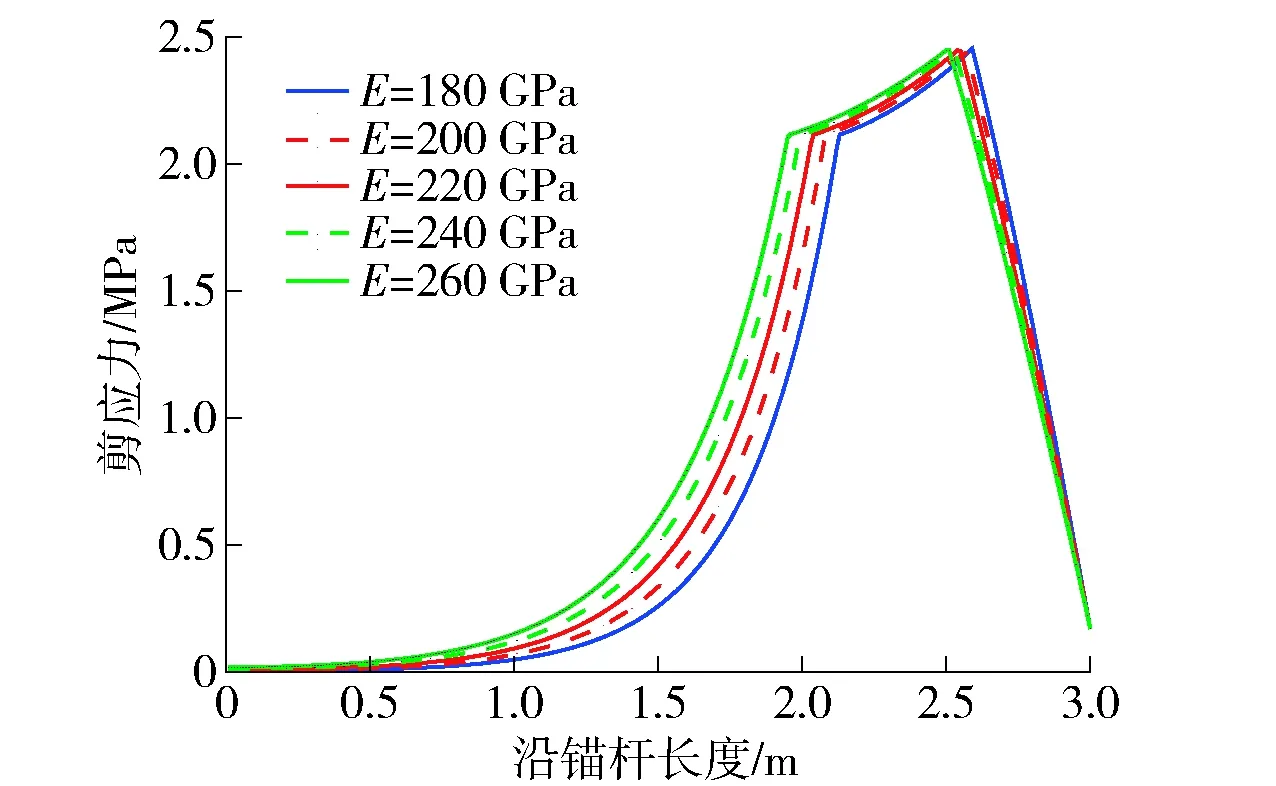
图14 锚杆弹性模量对剪应力沿全长分布影响Fig.14 Effect of the bolt Young’s modulus on shear stress distribution along the length of the bolt

3.3 锚杆半径

图16表示了锚杆半径对荷载- 位移曲线的影响.可以看出，极限荷载随着锚杆半径的增大而增大，且锚杆半径的增加对于脱黏阶段的锚杆延性有较大的限制作用.

图17、18给出了在弹性- 剪胀- 软化阶段加载端相同位移下，锚杆半径对应力沿着锚杆全长分布规律的影响.图17表明了锚杆半径越大，锚杆全长越早地进入弹性- 剪胀- 软化阶段，且剪应力峰值越早地向远离加载端移动.图18表明了在弹性阶段相同位置的轴应力随着锚杆半径增大而增大，但锚杆半径对该阶段轴应力峰值呈负相关，而对峰值剪应力与残余剪应力没有影响.

图16 锚杆半径对荷载- 位移曲线的影响Fig.16 Effect of the bolt radius on load-displacement curves

图17 锚杆半径对剪应力沿全长分布影响Fig.17 Effect of the bolt radius on shear stress distribution along the length of the bolt

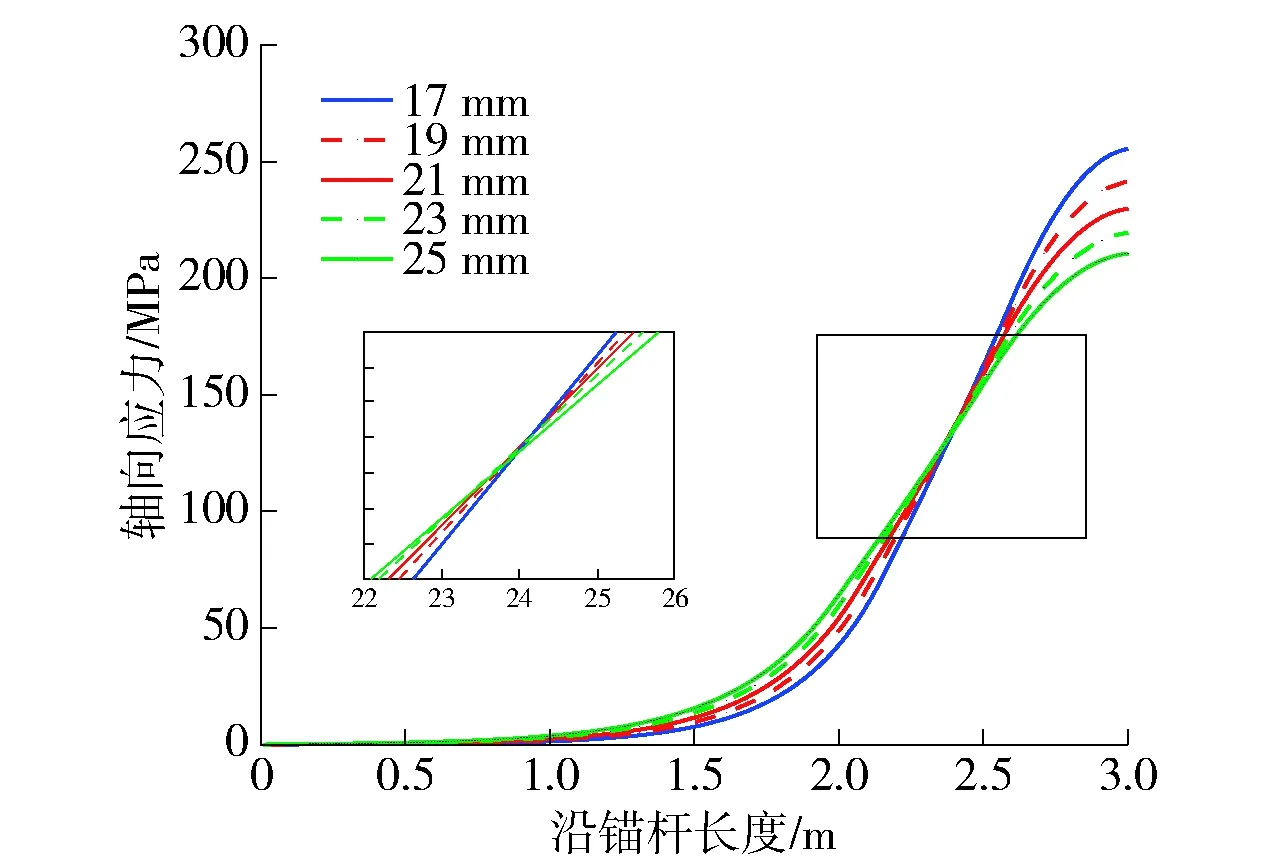
图18 锚杆半径对轴向应力沿全长分布影响Fig.18 Effect of the bolt radius on axial stress distribution along the length of the bolt

4 结论

文章利用四线性黏结滑移本构模型修正了前人提出的荷载- 位移解析方程，建立了锚杆受拉拔荷载作用下渐进失效的全过程分析方法，并为剪胀- 软化- 脱黏阶段、软化- 脱黏阶段和完全脱黏阶段的应力分布、荷载- 位移曲线提供封闭形式的表达式.根据文中提出的假设和讨论，可以得出以下结论：

1) 修正后的荷载- 位移曲线解决了间断突变的问题，且预测效果优于三线性黏结滑移模型所推导的荷载- 位移曲线.

2) 沿锚杆全长轴向应力和界面剪应力分布与实测数据吻合较好.

3) 锚杆半径、弹性模量的增大提高了极限荷载，且对锚杆延性有较大的限制作用.

4) 弹性阶段、弹性- 剪胀阶段和弹性- 剪胀- 软化阶段的荷载- 位移曲线与锚固长度无关，当锚固长度较小时，整个锚固范围内的承载能力得到充分发挥，当锚固长度过长时，整个锚固界面承载潜力的发挥程度将与锚固长度无关.

5) 锚杆弹性模量和锚杆半径越大，锚杆全长越早地进入弹性- 剪胀- 软化阶段，且剪应力峰值越早地向远离加载端移动.弹性区域的剪应力随着锚杆弹性模量增大而增大，而在剪胀区域弹性模量对剪应力值大小的影响程度降低.弹性模量对轴应力峰值呈正相关，但锚杆半径对轴应力峰值呈负相关，而弹性模量和锚杆半径对峰值剪应力与残余剪应力均没有影响.