下穿施工时盾构- 卵石地层- 既有隧道相互作用模型试验研究

林庆涛, 路德春, 雷春明, 李晓强, 苗金波, 龚秋明, 杜修力

(1.北京工业大学岩土与地下工程研究所， 北京 100124;2.中国电力工程咨询集团新能源有限公司， 北京 100120)

我国城市中广泛分布着卵石地层.据统计，北京、兰州、沈阳、成都等20多个城市的地铁隧道穿越卵石地层[1].卵石地层中土颗粒之间孔隙较大，黏聚力接近于零，地层响应灵敏，开挖条件下容易发生塌落破坏，属于典型的力学不稳定层[2-5].盾构掘进时，在刀盘扰动和掌子面卸载共同作用下，容易发生地层塌陷事故[6-9].尤其是既有隧道存在时，如果不采取加固措施，盾构下穿施工导致地层发生坍塌破坏的可能性显著提高[9-10]，既有隧道可能产生不可恢复的扰动[11-14].

图1 清华园隧道与北京地铁10号线区间隧道的位置Fig.1 Positions of Qinghuayuan Tunnel and the interval tunnels of Beijing Metro Line 10

黏土或砂土地层中盾构下穿既有隧道的问题已经被广泛研究.这些研究主要关注盾构下穿过程中既有隧道的扰动特征，包括位移、附加应力和变形[15-21].对于卵石地层，多数研究关注于盾构掘进的控制，包括盾构施工参数的选择[3, 21]和渣土改良[22-24]；以及盾构掘进过程中卵石地层的扰动，如地表沉降[6, 25-26]和掌子面塌陷[27-28]特征.目前，关于卵石地层中盾构施工的研究还比较缺乏，尤其是卵石地层中盾构下穿既有隧道的研究.开展相关的研究，获得盾构下穿施工对既有隧道及其周围卵石土的扰动特征，以及既有隧道和卵石土体对盾构施工状态的影响规律，提出合理的盾构下穿施工方式，以及既有隧道及其周围的卵石土的加固措施，对实际工程的安全施工有重要的参考价值.

基于自主研发的土压平衡盾构试验平台，开展了卵石地层中盾构下穿既有隧道的模型试验.试验过程中，记录了盾构的施工动力，用于分析既有隧道的存在对盾构施工状态的影响；称量了螺旋出土器的排土量，用于揭示既有隧道周围卵石土体发生塌落破坏的原因；监测了地表沉降、作用在既有隧道上的土压力，以及既有隧道的应变，用于探究盾构下穿对卵石地层和既有隧道的相互作用机理.

1 工程背景

新京张铁路清华园隧道位于北京市海淀区，隧道入口位于学院南路北侧(DK14+090)，出口位于双清路北侧(DK19+420)，全长5 330 m，入口段(DK14+090～DK14+450)长度为360 m，中段(DK14+450～DK18+200)长度为3 750 m，出口段(DK18+200～DK19+420)长度为1 220 m.入口段和出口段采用明挖法施工，中段采用φ12.6 m的泥水平衡盾构施工.盾构开挖直径12.64 m，隧道采用外径12.2 m、内径11.1 m的衬砌支护[29].清华园隧道位于知春路地铁站西侧，由北向南下穿通过北京地铁10号线区间既有隧道.清华园隧道与既有隧道的夹角为79°.既有隧道位于知春路正下方，隧道顶部与知春路路面之间土层的厚度为9.18 m，如图1所示.

北京地铁10号线区间既有隧道采用浅埋暗挖法施工，采用复合式衬砌支护，隧道横断面为马蹄形，其高度×宽度为6.7 m×6.5 m.既有隧道的初衬为C25网喷混凝土，厚度为250 mm；二衬为300 mm厚的C30混凝土.新建隧道采用外径为12.2 m、内径为11.1 m的管片支护，每环管片宽度为2.0 m，由8个标准块和1个关键块拼装而成，相邻管片采用错缝拼装.新建清华园隧道拱顶埋深约为21.36 m，新隧道洞顶与既有隧道底板间距为5.48 m，如图1所示.建设清华园隧道时，盾构机在典型的北京砂卵石复合地层中施工.地层自下而上依次为人工填土层(2.2 m)、粉质黏土层(23.8 m)、中密卵石层(9.8 m)、粉质黏土层(2.5 m)、粉砂层(2.9 m)、密实卵石层.地下水位位于地表以下24.0 m左右.新建隧道洞顶位于中密卵石地层中，盾构掘进过程中刀盘前方土体可能发生坍塌破坏.

2 试验模型设计

利用自主设计的土压平衡盾构试验平台，基于背景工程和相似理论建立了试验模型，并开展了盾构下穿既有隧道的模型试验.试验过程中对盾构动力和排土量，以及地表沉降，作用在既有隧道上的土压力和既有隧道的应变进行了监测.

2.1 土压平衡盾构试验平台

如图2所示，试验平台由模型箱、盾构机和控制系统组成.模型箱内部尺寸为2.0 m×2.0 m×1.5 m(长×宽×高).盾构机由开挖机构、推进机构、出土机构和支护机构组成.开挖机构：刀盘为辐板式，外径为280 mm，开口率为45%，可实现正反转，转速精度为0.1 r/min，最大扭矩为1 800 N·m.推进机构：盾构推进利用长行程高精度丝杠实现，最大推力为60 kN，行程为2 200 mm，掘进速度精度为0.1 mm/min.出土机构：螺旋出土器为轴式，外径为64 mm，可排出直径10 mm的土颗粒，转速范围为0～50 r/min，最大扭矩为60 N·m.支护机构：盾壳外面设置隧道衬砌，其外径为280 mm，厚度为12 mm，与盾壳间隙为10 mm，采用低密度聚乙烯(LDPE)制作.LDPE密度为0.91～0.93 g/cm3，弹性模量为172 MPa，其几何尺寸和力学性能基本满足相似理论的要求.控制系统可以实现盾构施工参数的控制和存储.

图2 土压平衡盾构试验平台Fig.2 Test platform for the earth pressure balance shield

2.2 试验模型

试验模型采用与盾构相同的几何相似常数设计，即Cl=45.试验模型尺寸为2 000 mm×2 000 mm×1 400 mm(长×宽×高)，如图3所示.盾构隧道直径280 mm，洞顶埋深620 mm.试验模型中左侧既有隧道参照北京地铁10号线设计，横截面为马蹄形；为了研究隧道横截面形状的影响，既有隧道右线设计为矩形隧道.2条既有隧道的高度×宽度都为138 mm×144 mm，两隧道轴线之间的水平距离为400 mm.同时，两既有隧道埋深相同，底板与新建盾构隧道顶部之间土体的厚度为122 mm.新建盾构隧道与既有隧道空间位置如图3所示.

图3 试验模型布置及尺寸(单位：mm)Fig.3 Layout and dimensions of the test model (unit: mm)

2.2.1 相似卵石地层

实际工程中盾构主要在卵石地层中掘进，同时既有隧道正好位于卵石地层上方，盾构施工时既有结构的扰动程度主要取决于卵石地层的扰动，因此试验中将地层简化为单一的卵石地层.根据相似理论，岩土工程试验中土体应该满足土体颗粒几何相似和物理力学特性的相似.土体的一些力学参数，包括临界应力比M、泊松比ν，初始孔隙比e0量纲为1，相似常数为1；另外一些力学参数(如压缩指数λ和回弹指数κ)的相似常数难以确定.土颗粒粒径大小对其物理力学特性有着重要影响，模型试验中实现土颗粒粒径几何相似十分必要.砂土和黏土颗粒粒径较小，试验中很难实现其颗粒粒径的相似，但是对于卵石地层土颗粒的几何相似可以实现.因此，试验中根据几何相似比1/45对实际工程卵石颗粒进行缩尺得到了相似卵石地层的级配.

在实际工程中，卵石土的颗粒直径为60～150 mm、20～60 mm和0～20 mm，质量占比分别为55%、15%和30%.采用3种不同粒径范围的砂配置相似的卵石层，达到目标级配时，3种砂的质量比m(粗砂)∶m(细砂1)∶m(细砂2)=1.129∶1.097∶1.000.试验用土的级配曲线如图4所示.配置好的卵石土不均匀系数Cu=3.91<5，曲率系数Cc=1.02>1.试验土体的力学参数见表1.

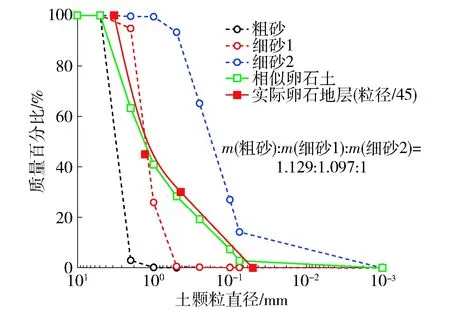
图4 实际卵石和试验用土的级配曲线Fig.4 Grading curves of the field cobble strata and test soil

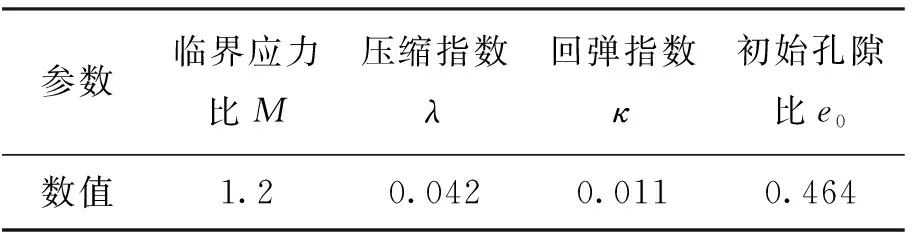
表1 相似卵石土力学参数

2.2.2 模型隧道

实际工程中，既有隧道的变形通常处于弹性变形阶段，因此模型隧道的尺寸和弹性模量应满足相似理论的要求.模型隧道的几何相似常数为Cl=45，弹性模量的相似常数为CE=CγCl.在该相似常数时，LDPE是制作模型隧道的理想材料，因此既有的模型隧道采用LDPE制作，如图5所示.

图5 制作完成的既有隧道Fig.5 Model tunnels in the test

模型隧道制作完成后，对其纵向抗弯刚度进行测试.测试过程中，将既有隧道当作简支梁，在其中间横截面顶部逐级施加荷载，以获得其挠度.模型隧道的纵向抗弯刚度可利用

(1)

计算.式中ω是模型隧道的挠度.加载至109.07 N时，马蹄形隧道和矩形隧道的相应挠度分别为1.07、0.56 mm，以此为基础计算两隧道的纵向抗弯刚度分别为8 831.6、15 405.14 Pa·m4.

2.3 监测方案和试验过程

在试验过程中，对地表沉降、作用在既有隧道上的土压力，以及既有隧道的应变进行了监测.设置SD1、SD2、SD3、SD4、SD5五个横向监测断面测量地表沉降，这些监测断面分别位于盾构掘进距离y为300、785、1 000、1 215和1 700 mm的位置，其中y=785、1 215 mm监测断面分别对应于马蹄形隧道和矩形隧道轴线正上方，监测点位置如图6(a)所示.同时，在马蹄形和矩形隧道上设置9个监测断面，测量其纵向变形，如图6(b)所示；在两既有隧道的顶拱、底板和两侧墙的外表面设置土压力传感器和应变片，测量作用在中间横截面上的法向土压力和其环向变形，如图6(c)(d)所示.模型试验中，地表位移采5G106直线位移计测量，量程50 mm，测量精度0.25%FS，无限分辨率.土压力采用应变式微型土压力盒测量，量程50 kPa，测量精度0.5%FS.DH3816N静态应变采集仪被用于采集和记录传感器的数据，采集仪频率1～200 Hz，采集范围±3×10-2ε，分辨率1×10-6ε.

图6 试验模型监测方案Fig.6 Monitored scheme of the test model

试验模型采用逐层压实法填筑.填筑每层时，首先称量724 kg的试验土体，并倒入模型箱中铺成厚度均匀的一层，然后在其上方悬挂水平弹性绳，测试该层的平整度.之后，将试验土压实至预设标高.试验土体干密度为1 800 kg/m3，相对密实度为55%.当填土厚度分别达到30、50和80 cm时，埋入铝盒测量填土的密度.当填土厚度达到90 cm时，将2个模型隧道放置在设计位置，如图7(a)所示.然后，根据监测方案将土压力传感器固定在模型隧道上，如图7(b)所示.在此之后，继续填土直到完成试验模型.最后将位移计安装在设计位置，如图7(c)所示，并将位移计和土压力传感器的信号线与采集仪相连，如图7(d)所示，并根据试验要求对采集系统进行设置和调试.

图7 试验模型建立过程Fig.7 Establishment process of the test model

3 试验结果分析

基于盾构下穿施工引起的地表沉降、作用在既有隧道上的土压力，以及既有隧道的应变的监测数据，分析了盾构开挖、卵石土体和既有隧道之间的相互作用.

3.1 既有隧道对盾构开挖的影响

盾构掘进时需要的施工动力与作用在盾壳和刀盘上的土压力有关，土压力越大，盾构开挖掘进所需要的刀盘扭矩和推进力越大.新建隧道上方的既有隧道为中空结构，其整体质量较小，因此既有结构下方土体的压力比无既有结构位置同埋深处土体的压力低；同时既有隧道刚度较大，开挖扰动后起到横梁的作用阻止其上部土体的土压力作用在盾构机上.因此，盾构下穿既有隧道时盾构机的推进力和刀盘扭矩会有一定程度降低，如图8所示.

图8 盾构掘进动力和排土量Fig.8 Shield motive power and weight of the discharged soil

另一方面，当施工参数不变时，土压力越大，土体流入土压力舱的速度就越快，盾构排土量也越大，土压力越小时则相反.图8给出了盾构掘进过程中螺旋出土器的排土量，可以看出刀盘在无既有隧道位置掘进时盾构排土量较为稳定，当盾构刀盘掘进至既有隧道附近时排土量逐渐减小，当盾构刀盘驶过既有隧道轴线后排土量又开始逐渐增加.也就是说，当盾构刀盘从既有结构下方驶出时，盾构开挖断面的地层损失会逐渐增大，以至于既有隧道盾构驶出侧的卵石土更容易发生塌落破坏.

3.2 既有隧道对地层变形的影响

图9给出了盾构掘进过程中螺旋出土器的排土量，以及开挖完成时刻对应位置处的地表沉降.可以看出，在无既有隧道的位置掘进时，盾构的排土量较为稳定，地表的沉降量很小；当下穿既有隧道时，盾构的排土量先减小再增加，表明盾构刀盘从既有结构下方驶出时，新建隧道开挖断面的地层损失会逐渐增大.同时，图9显示马蹄形隧道和矩形隧道盾构驶出一侧的地表都出现了塌陷破坏，可以推断地层损失的增加是导致这2个位置处地层发生塌陷破坏的重要原因.

图9 地表沉降和盾构机排土量Fig.9 Surface settlement and weight of the dischanged soil

图10 马蹄形隧道轴线横断面地表沉降Fig.10 Surface settlement of the transverse section of the horseshoe tunnel axis

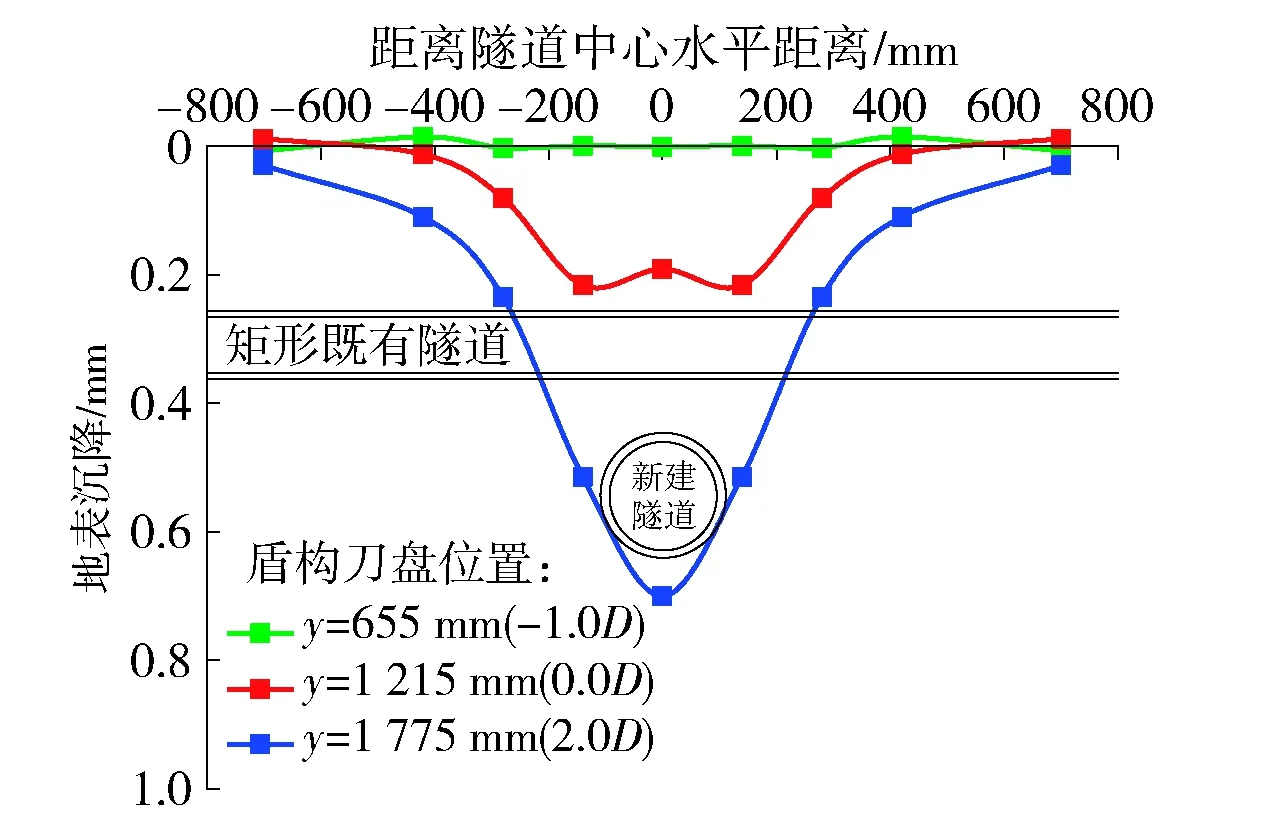
图11 矩形隧道轴线横断面地表沉降Fig.11 Surface settlement of the transverse section of the rectangular tunnel axis

同时，图10、11分别给出了马蹄形隧道和矩形隧道轴线所在横断面的地表沉降.对于马蹄形隧道轴线横截面，盾构刀盘掘进至y=505 mm(-1.0D)时，地表开始出现沉降；刀盘掘进至y=1 345 mm(2.0D)时，地表沉降不再增加；刀盘掘进至y=785 mm(0.0D)时，地表塌陷还未发生，此时地表沉降远小于刀盘掘进至y=1 345 mm时的值.同时可以看出，盾构掘进的过程中既有隧道对其正上方土体的沉降有一定的阻拦作用，刀盘驶过马蹄形隧道轴线之前既有隧道和新建隧道相交位置处地表的沉降与其附近位置的沉降接近，但由于塌陷破坏的发生，该点的最终沉降远大于其他位置.对于矩形隧道轴线横断面，位移计所在位置土体未发生塌落，地表沉降量较小.盾构刀盘掘进至y=655 mm(-2.0D)时，该横截面开始出现地表沉降；刀盘掘进至y=1 775 mm(2.0D)时，地表沉降不再增加.矩形隧道对其正上方地表沉降发展的影响与马蹄形隧道相似，如图11所示.

3.3 地层对既有隧道变形的影响

既有隧道周围土体发生变形的同时，作用在既有隧道上的土压力也发生变化，从而导致既有结构产生附加变形.作用在马蹄形隧道拱顶和拱底的土压力沿其轴线方向的分布如图12所示，相对应的马蹄形隧道的纵向变形如图13所示.图12(a)显示，随着盾构掘进，作用在马蹄形隧道顶板的土压力逐渐增大，距离中间截面越远的位置增加量越小；图12(b)为作用在马蹄形隧道底板的土压力，在中间横截面处，随着盾构掘进土压力逐渐减小，在x=±140 cm位置处土压力随着盾构掘进先增大后减小，在x=±420 cm处土压力逐渐增大.图12中呈现的土压力的变化规律表明，马蹄形隧道中间横截面附近产生向下的挠度，呈现顶板受压底板受拉的变形模式；远离中间横截面的位置产生向上的挠度，呈现顶板受拉底板受压的变形模式，如图13中的纵向应变结果所示.

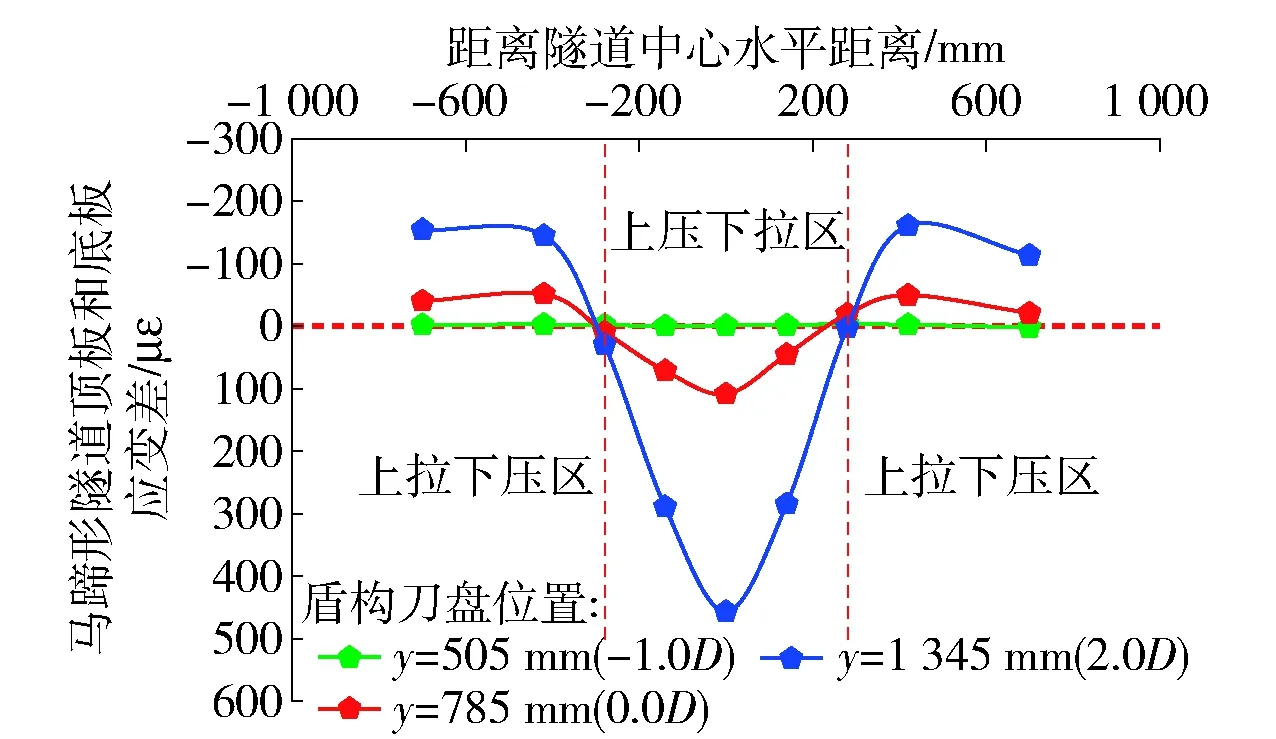
图13 马蹄形隧道纵向应变Fig.13 Longitudinal strain of the horseshoe tunnel

作用在马蹄形隧道中间横截面拱顶、拱底，以及两拱腰的土压力随盾构掘进的变化如图14所示.刀盘掘进至马蹄形隧道轴线之前，拱底和两拱腰的土压力逐渐减小，但左拱腰和拱底土压力的减小更为显著，拱顶土压力变化较小；刀盘通过轴线后，右拱腰土压力进一步减小，拱顶土压力显著增加，左拱腰和拱底则变化不大.盾构掘进至马蹄形隧道轴线和通过轴线2.0D后，马蹄形隧道的环向应变也展示在了图13中，可以看出盾构掘进至马蹄形隧道轴线之前，马蹄形隧道近似沿135～315°轴线方向被压扁，盾构开挖完成后马蹄形隧道压扁的轴线方向变为22.5～202.5°.马蹄形隧道中间截面变形随盾构掘进的演化与该截面上土压力的变化趋势一致.

矩形隧道纵向变形如图15所示，在x=±420 mm之间，随着盾构掘进矩形隧道顶板受压、底板受拉的变形特征更加显著；在x=±420 mm之外，矩形隧道受到的扰动较小.作用在矩形隧道中间横截面拱顶、拱底，以及两拱腰的土压力随盾构掘进的变化规律与马蹄形隧道相似，但是矩形隧道的环向变形与马蹄隧道差别较大，如图16所示.盾构刀盘掘进至矩形隧道轴线之前，矩形隧道近似在竖直方向上被压扁，但其顶板的变形较为复杂，同时左侧墙的变形程度远大于右侧墙；盾构刀盘通过矩形隧道轴线之后，矩形隧道右侧墙的变形显著增加，最终左右侧墙都呈现显著的外拉内压变形，矩形隧道表现为竖直方向压扁、水平方向拉长的变形特征.

图14 马蹄形隧道中间截面的法向土压力变化及其环向应变Fig.14 Circumferential earth pressure and strains of the horseshoe tunnel

图15 矩形隧道纵向应变.Fig.15 Longitudinal strain of the rectangular tunnel

4 结论

基于自主研发的土压平衡盾构试验平台，开展了卵石地层盾构穿下穿既有隧道模型试验，获得了下穿施工过程中盾构的推进力、刀盘扭矩和排土量，监测了地表沉降、既有隧道应变，以及作用在既有隧道上的法向土压力.以此为基础，分析了盾构- 卵石地层- 既有隧道的相互作用机理.主要结论如下.

1) 盾构开挖引起地层损失，使得刀盘周围的土体产生变形，同时作用在既有隧道上的土压力重新分布，既有隧道发生附加变形.既有隧道使作用在盾壳和刀盘上的土压力减小，盾构下穿既有隧道时掘进力和刀盘扭矩出现一定程度降低，同时使得刀盘驶入既有隧道下方时盾构排土量减小，从既有隧道下方驶出时排土量增加，以至于既有隧道盾构驶出一侧土体的扰动程度更大.卵石地层受扰动时易发生塌落破坏，因此盾构在卵石地层中下穿既有隧道时，既有隧道盾构驶出侧的土体更易发生塌落破坏.同时，卵石地层成拱能力较强，地层塌落破坏发展至地表存在滞后性.伴随着地层塌落的发展，作用在既有隧道上的土压力不断变化，既有隧道的变形也继续发展，直至地层塌落破坏不再发展.

图16 矩形隧道的法向土压力变化以及环向变形Fig.16 Circumferential earth pressure and strains of the rectangular tunnel

2) 盾构下穿过程中马蹄形隧道和矩形隧道的纵向变形相似，但是两既有隧道中间横截面的环向变形差别显著.对于纵向变形：两既有隧道最大拉应变都发生在中间横截面的拱底位置，环向的拉伸裂缝在该位置处最先产生.对于环向变形：盾构刀盘掘进至既有隧道轴线下方时，马蹄形隧道的右拱肩和左拱脚的拉应变最大，矩形隧道左拱腰的拉应变最大；盾构刀盘远离既有隧道轴线2.0D时，马蹄形隧道拉应变最大的位置转移至左拱肩和右拱脚，矩形隧道右拱腰拉应变超过左拱腰.对于马蹄形隧道和矩形隧道发生纵向拉伸裂缝的位置显著不同，现场施工时需要关注的位置不同.盾构下穿过程中，作用在马蹄形隧道中间横截面和矩形隧道中间横截面的围岩压力的变化规律相似，截面形式的不同是导致2个既有隧道变形显著不同的主要原因.

3) 由于土体变形具有强非线性的特征，模型试验中土体难以完全满足相似理论的要求，以至于模型试验结果与现场工程结果存在差异.但是对于试验模型和现场工程相对应位置处土体，其变形趋势相同，模型试验的结果可以定性地揭示现场工程中地层和结构的受力变形规律，从而为实际工程的施工提供一定指导.