NOMA-Based UAV Communications for Maritime Coverage Enhancement

Rui Tang,Wei Feng,*,Yunfei Chen,Ning Ge

1 Department of Electronic Engineering,Tsinghua University,Beijing 100084,China

2 School of Engineering,University of Warwick,Coventry CV4 7AL,UK

Abstract:The lack of communication infrastructure in the ocean inevitably leads to coverage blind zones.In addition to high-throughput marine satellites,unmanned aerial vehicles(UAVs)can be used to provide coverage for these blind zones along with onshore base stations.In this paper,we consider the use of UAV for maritime coverage enhancement.Particularly,to serve more ships on the vast oceanic area with limited spectrum resources,we employ non-orthogonal multiple access (NOMA).A joint power and transmission duration allocation problem is formulated to maximize the minimum ship throughput,with the constraints on onboard communication energy.Different from previous works,we only assume the slowly time-varying large-scale channel state information (CSI) to reduce the system cost,as the large-scale CSI is locationdependent and can be obtained according to a priori radio map.To solve the non-convex problem,we decompose it into two subproblems and solve them in an iterative way.Simulation results show the effectiveness of the proposed solution.

Keywords:large-scale channel state information(CSI);maritime communications;non-orthogonal multiple access (NOMA);unmanned aerial vehicle(UAV)

I.INTRODUCTION

With the rapid development of ocean observation,shipping industry,marine resource exploitation,and other maritime activities,the demand for broadband communication services on the ocean grows rapidly [1].In addition to high-throughput marine satellites,the shore-based communication network (SBCN) is currently the main approach to realize broadband communications for the coastal area.By building terrestrial base stations (TBSs) along the coastline,fourthgeneration(4G)and fifth-generation(5G)cellular coverage can be extended to the ocean[2].

The key limitation of SBCN lies in the geometrically limited base station(BS)sites.In practice,TBSs should be deployed on mountains or elevated towers.Both power supply and fiber backhaul are necessary to support a vital TBS.This limits the number of possible BS sites,which inevitably leads to blind zones even near the coastline.To provide coverage for these blind zones,shipborne BSs have been employed in [3],in which the relaying communication infrastructure may also be deployed on buoys and unmanned ships.However,this vessel-based approach requires high-density vessels to maintain the connectivity on the vast ocean.Furthermore,many vessels follow fixed shipping lanes in real world.Thus,it is difficult to achieve a desirable network topology.

Unmanned aerial vehicles(UAVs)are promising to provide an on-demand broadband maritime coverage due to their agile mobility [2].When deployed as aerial BSs on the ocean,UAVs have a much wider coverage range than TBSs.Moreover,UAVs are highly maneuverable and cost-effective,which are thus suitable for various mission-critical applications[4,5].According to shipping lane information,the distribution and number of users in blind zones can be obtained in advance,and the use of UAV for maritime communication can provide high-quality and fair coverage for these users with weak channel condition.Currently,most research efforts on UAV communications have focused on the terrestrial scenario,and there remain open challenges to build an efficient maritime UAV communication system,due to the unique environments on the ocean and energy constraints of UAVs as follows.

On one hand,UAVs are required to provide highquality communication services for distributed ships within a vast area.Unlike terrestrial users,maritime users have a large variation in location and communication demand,and the corresponding channel state information (CSI) is also largely different [6].Thus,the diversity of users should be fully considered in the design of UAV-enabled coverage enhancement.On the other hand,both the communication energy and propulsion energy of UAVs are limited [4].It is difficult to recharge the onboard batteries after a UAV is dispatched.Thus,the communication energy constraints should be considered and the transmission duration for different ships should be carefully scheduled.Motivated by these,we will use non-orthogonal multiple access(NOMA)technology to serve different ships with limited onboard UAV energy.Compared with orthogonal multiple access (OMA),NOMA allows users to share non-orthogonal resources to improve spectral efficiency with the aid of successive interference cancellation (SIC) [7].Ships have more powerful computation capability than conventional mobile users;thus,complicated SIC is affordable for downlink maritime communications.Also,due to the sparsity of ship distribution on the vast ocean,there is significant difference between ship channels so that NOMA fits well with promising performance gains[8].

There have been several works on NOMA-based UAV communications for the terrestrial scenario [9–12].The authors of[9]jointly designed the placement and transmission power of a UAV to maximize the sum rate of a NOMA-UAV network.In [10],the authors investigated the outage probability of two ground users with NOMA in a UAV-enabled downlink wireless system.In [11],a power allocation scheme was proposed to optimize the sum rate with a guaranteed minimum user rate.Further for a multiuser communication system,the authors of [12]formulated a maxmin rate optimization problem by jointly optimizing the UAV altitude,transmit antenna beam width,power and bandwidth.These works provide useful insights on NOMA-based UAV for terrestrial communications but none of them has considered its use on the ocean.In maritime communications,the maritime channel fading consists of both large-scale and small-scale fading.It is usually challenging to acquire full CSI due to the dynamic property of small-scale fading and limited feedback cost of CSI on the vast oceanic area.Thus,we can only use the large-scale CSI,which varies slowly and is location-dependent.We may easily obtain the large-scale CSI according to a priori radio map [2].Although the large-scale CSI has been exploited in UAV communications for the Internet of Things[13],its potential gain in a NOMA regime remains unknown to our knowledge.

In this paper,we focus on a NOMA-based UAV system to cover the blind zones of existing TBSs in maritime communications.The main contributions of this paper are summarized as follows.

• We establish a NOMA-based maritime UAV communication model,where maritime users are divided into groups based on their relative locations[14],and a maritime UAV sequentially hovers to serve multiple groups of users by adopting NOMA techniques.Motivated by practical applications,we consider both the communication energy and transmission duration constraints of UAV,and assume only the slowly-varying largescale CSI is available.

• We formulate a joint transmit power and transmission duration allocation problem to maximize the minimum ship throughput.The optimization objective is to provide high-quality and fair coverage for users located in the blind zones.The problem is non-convex.We decompose it into a transmit power allocation subproblem and transmission duration assignment subproblem,and solve these subproblems in an iterative way.

• We validate the proposed scheme by simulations,and also illustrate the impact of system parameters on the coverage performance,including the total transmission duration,the hovering location and the altitude of UAV.These results provide guidelines for the design of NOMA-based maritime UAVs.

The remainder of the paper is organized as follows.Section II introduces the system model of NOMA-based maritime UAV communications.Section III formulates the coverage optimization problem and shows an iterative algorithm to solve it.Simulation results are presented in Section IV to evaluate the performance of the proposed algorithm.Finally,Section V presents the conclusion.

II.SYSTEM MODEL

The NOMA-based maritime UAV communication model is shown in Figure1.To reduce the system cost,we assume that there exists a single rotary-wing UAV that serves multiple ships located in the blind zones.The UAV and ships are both equipped with a single antenna.

Figure1.Illustration of a NOMA-based maritime UAV communication model.

To cover blind zones within a vast oceanic area,we divide all vessels intoKNOMA-based vessel groups withNships in each group.The prior position information of vessels is used to guarantee that each group contains both nearby and far vessels to the coastline.

The rotary-wing UAV hovers at given locations forKtimes to serve vessel groups in turn under NOMA regime,and the flight trajectory is predefined[15].

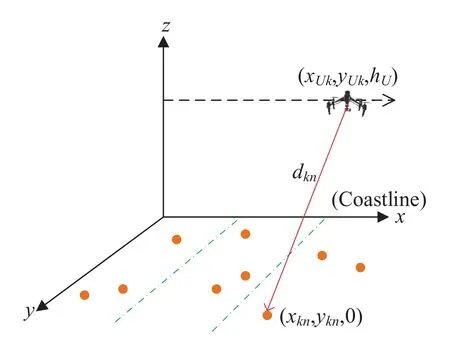
Figure2.Illustration of a maritime UAV communication scenario.

As illustrated in Figure2,we consider a threedimensional(3D)Cartesian coordinate system,where the coastline is approximated as thexaxis and theyaxis extends into the ocean.The starting coordinate of UAV flight is(0,0,hU),wherehUdenotes the UAV altitude.Thekth hovering location of UAV is(xUk,yUk,hU).According to the priori radio map,we can obtain the locations of ships to be served,and the coordinate of shipnin groupkis(xkn,ykn,0).

Thus,the distance between the UAV and shipnin groupkis

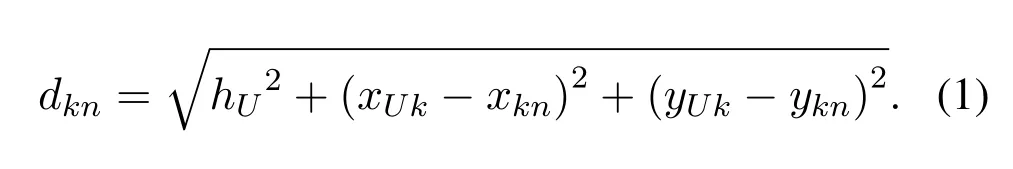
Due to limited endurance,transmission duration scheduling is a key consideration in the design of UAV-enabled coverage enhancement.Denote the transmission duration for groupkasτk,which satisfies

whereTdenotes the total transmission duration of UAV,andτbudgetdenotes the transmission duration budget.

Considering the peak transmit powerPTof a UAV,we have the transmit power constraint for the served group as follows

wherepkndenotes the transmit power allocated to shipnin groupk.Since the transmission duration is short enough,we assume thatpknis constant duringτk.

For battery-powered rotary-wing UAVs,the limited on-board energy consists of the propulsion energy and the communication energy.The former is used to maintain the state of motion during flight and is almost independent of communication.While the communication energy plays a vital role in the coverage enhancement,it is far less than the propulsion energy[16].

Based on these facts,we regard the propulsion energy as a constant,and mainly focus on the communication energy as

whereETdenotes the total communication energy of UAV.

Due to the special maritime propagation environment,a composite air-to-sea channel model with large-scale and small-scale fading is adopted.

The air-to-sea channel is dominated by the lineof-sight(LOS)and non-line-of-sight(NLOS)components,where the probability of LOS mainly depends on the density and height of scatterers in the coverage area and the elevation angle of the ship to UAV [12].The large-scale fading coefficient between UAV and shipnin groupkcan be written as[17,18]

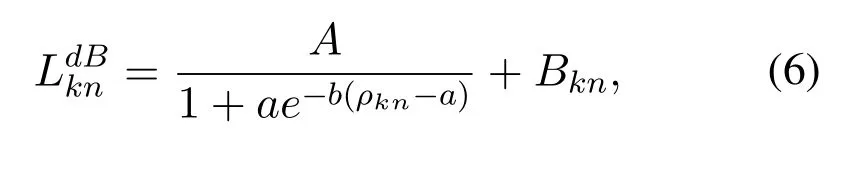
where

wherefis the carrier frequency,cis the speed of light,andηLOS,ηNLOS,aandbare constants related to the propagation environment.

Therefore,the large-scale channel fading is derived as

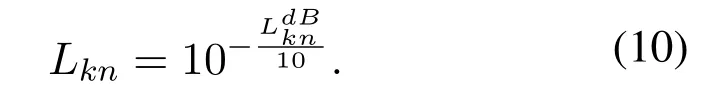
The small-scale channel fadingsknfollows the complex Gaussian distributionCN(0,1).The overall channel gain can be represented as

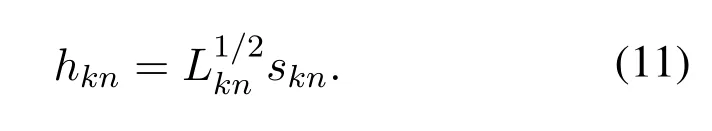
The received signal of shipnin groupkcan be expressed as

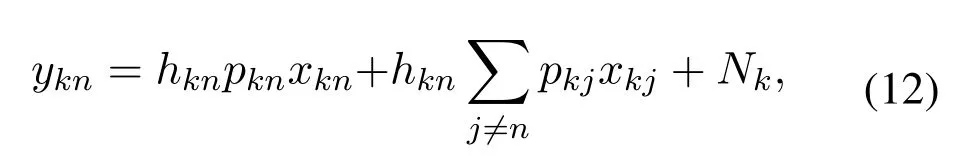
wherexknis the transmitted signal,which satisfies E(|x|2)=1,we denote E{·}as the expectation operation.AndNkrepresents the additive white Gaussian noise(AWGN)following complex Gaussian distributionCN(0,σ2N).

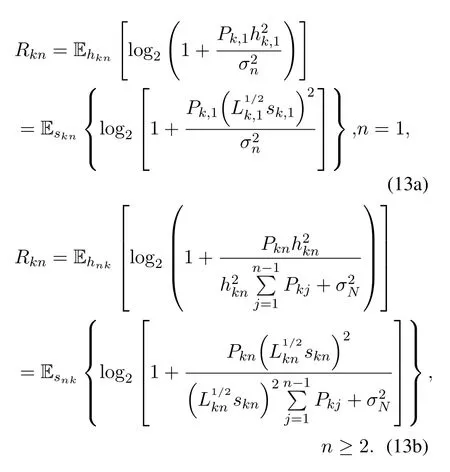
Without loss of generality,we assume that the channel conditions of the users in groupksatisfy|hk,1| ≥|hk,2|≥···≥|hkN|.

The achievable ergodic rate for shipnin groupkcan be expressed as

III.UAV ON-DEMAND COVERAGE OPTIMIZATION

In this section,we first formulate a coverage optimization problem to maximize the minimum throughput in the system by jointly optimizing the transmit power and transmission duration.The communication energy and transmission duration constraints are considered.

As a multivariable max-min problem,it is not so amenable to solve by traditional optimization methods.Moreover,the large variation of maritime users leads to the lack of user fairness easily.Thus,the user fairness should be fully considered in the solving process.

3.1 Problem Formulation

The coverage optimization problem is formulated as

whereτ=[τ1,τ2,···,τK]Tis the set of transmission duration,andP={pkn}K×Nis the set of transmit power matrices.

This problem is non-convex due to the nonconvexity ofRkn[19].Besides,the optimization variablesτandPare coupled because of (14f).Due to the expectation operator involved in(13),the objective function in(14a)is an implicit expression of variableP.

To solve the problem,we use an approximation of the achievable ergodic rate as the approximated optimization objective to simplify complex problem.Then,we adopt the block coordinate descent method to solve the problem iteratively.

Moreover,Considering the mathematical properties of the max-min problem,the throughput of all users should be kept as equal as possible when the optimal solution to (14) is achieved,where the coverage for blind zones can be fairer.

3.2 Iteratively Resource Allocation Algorithm

To decompose problem(14),we first fix the transmission durationτ;then,the power allocation subproblem can be written as

During transmission for any group,we can allocate the transmit power to intragroup users to guarantee fairness in the same group.Then,the total communication energy is allocated to all groups for the whole fair coverage performance,where the group with overall minimum throughput achieves the maximum.

Based on the analysis above,we can decompose the power allocation problem (15) into an intragroup power allocation subproblem and an intergroup power allocation subproblem,then solve them one at a time by utilizing their own properties.

Additionally,when the transmit powerPis fixed,we can easily obtain the optimal transmission duration for each group.

It is worth noting that the non-convex max-min subproblem is still intractable.Fortunately,we can prove that the optimal solution to the max-min problem can be obtained when the optimization variables of the user with a minimum throughput reaches the optimization space limit.

3.2.1 Intragroup Power Allocation

For groupk,given the allocated communication energyEkand transmission durationτk,the intragroup power allocation subproblem can be written as

wherePk=[pk,1,pk,2,···,pkN]Tdenotes the set of transmit power for groupk.

Problem (16) is intractable due to the expectation operation in(16a).Considering the property of smallscale CSI,we can obtain the upper bound on achievable ergodic rate by Jensen’s inequality[20,21]as

Considering the property of Jensen’s inequality,the upper bound in (17a) is relatively tight in low SINR,which is suitable for the maritime UAV communication scenario.Based on the theory in [21,22],we can introuduce an approximation of achievable ergodic rateRukn ≈Rknas follows.

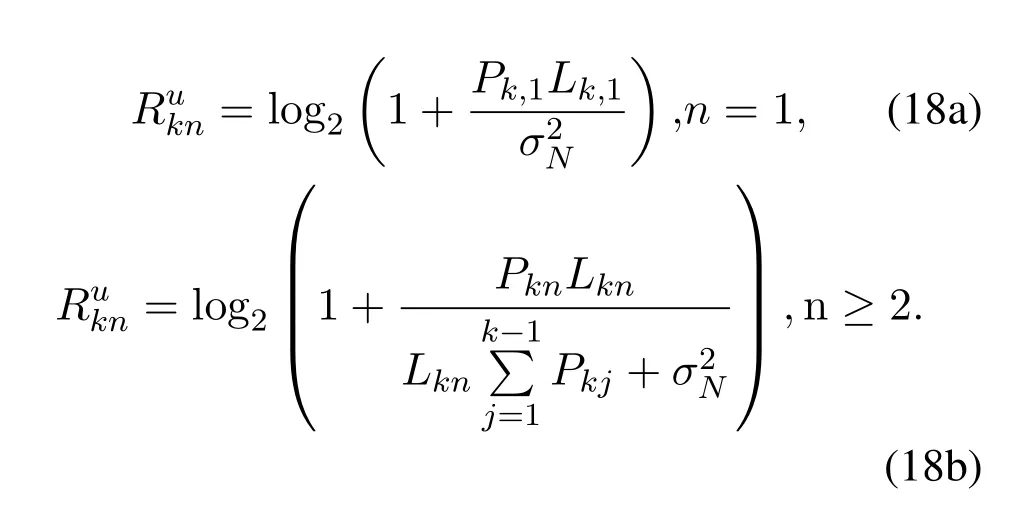
Then,by introuducing the approximation of achievable ergodic rate,we define a new optimization problem as

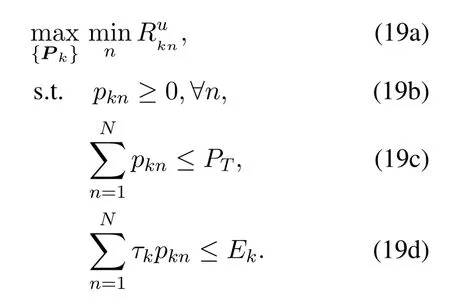
The solution to(19)is suboptimal to the intragroup power allocation subproblem(16)due to the approximation.

However,problem(19)is still non-convex and hard to solve.Through analysis,we can prove that the optimal solution to (19) is achieved only when all intragroup users have equal approximations of rate and the sum of transmit power reaches the allowable maximum transmit power,which can be represented as follows

By using the theory in [23],we can fix the equal intragroup user rate for groupkas the optimal approximation of rateR∗k=Ruk1=Ruk2=···=RukNand substitute the result into(18),therefore we obtain the following result

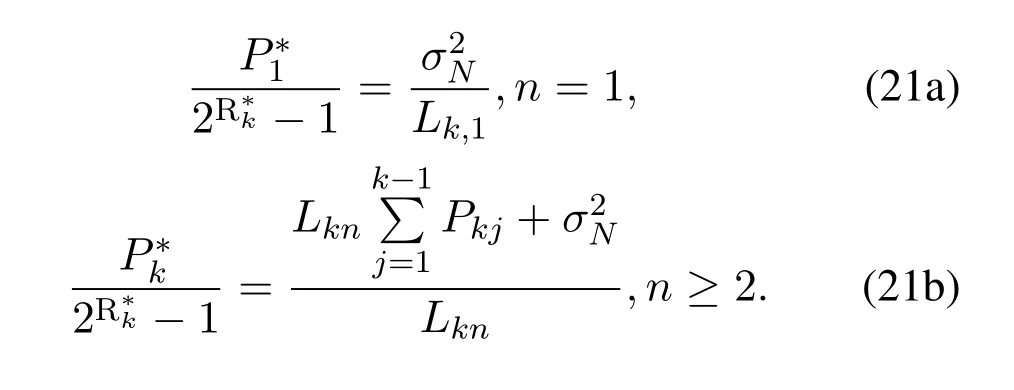
Then,by convert the expression(21),we can derive an eigenvalue equation of a matrixArelated toas follows

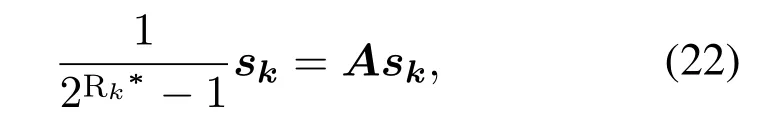
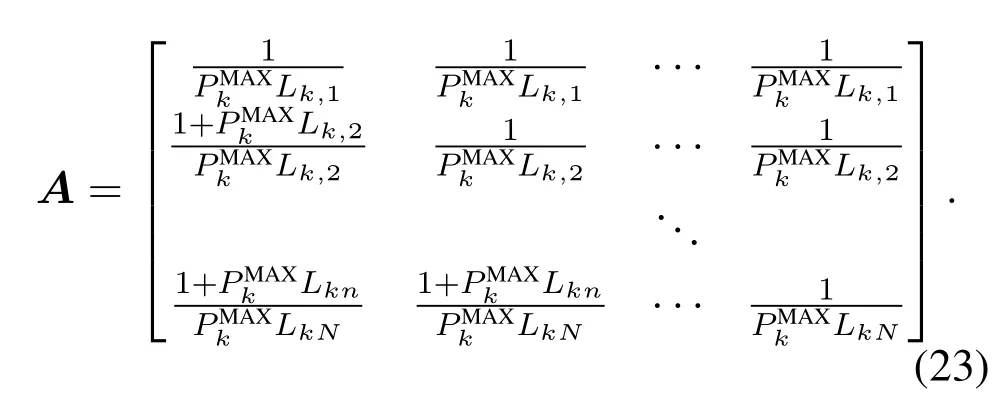
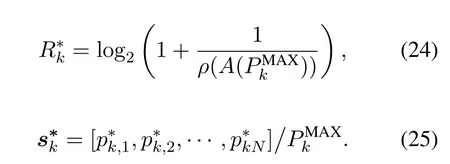
Based on the Perron-Frobenius theorem[23],we can derive the solution to(19)by intragroup power allocation algorithm,the procedures are presented in algorithm 1.

?

Proposition 1.The intragroup power allocation algorithm converges as fast as a geometric series[23].Proof.For the positive and regular matrixA,we denoteNeigenvalues and eigenvectors ofAasρ1,ρ2,···,ρNandw1,w2,···,wNrespectively,where|ρ1| ≥|ρ2| ≥··· ≥|ρN|,w1=s∗.The independent eigenvectors can be regarded as a set of basis function.Then,we can define an iterative vectors(i),which satisfies

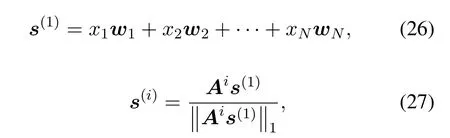
wherex1,x2,···,xNare scalars,ands(i)is consistent with the iterative process in algorithm 1.By multiplying(26)byAi,we have

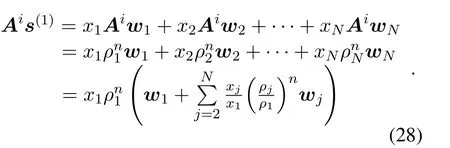
As the numbers of iterationsi →∞,(ρi/ρ1)i →0,and the iterative vector has

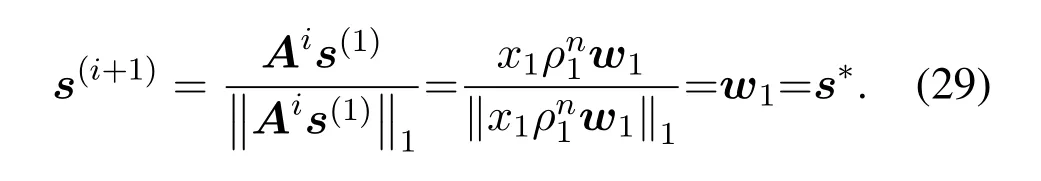
It is clear that the iterative vectors(i)converges tos∗as fast as a geometric series.

3.2.2 Intergroup Power Allocation

According to 3.2.1,we can obtain the optimal intragroup users’ rateR∗kfor groupk,which is related toThen,the intergroup power allocation problem is formulated as

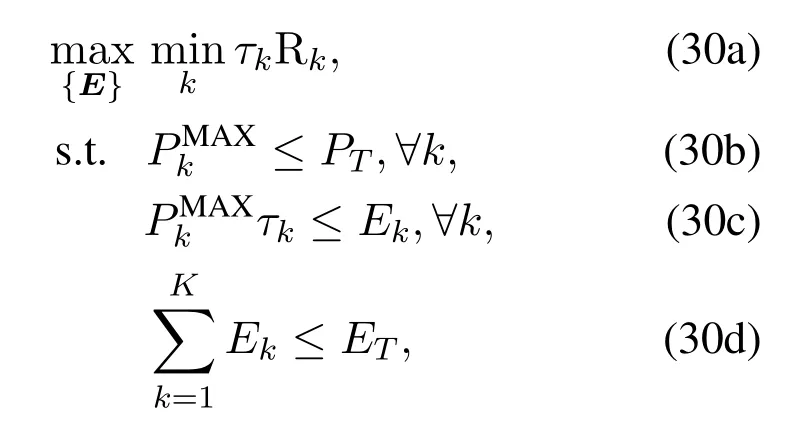
whereR=[R1,R2,···,RK]Tdenotes the achievable ergodic rate of each group,which is implicit to the allocated energyE=[E1,E2,···,EK]T;thus,the problem(30)is difficult to solve directly.

According to the following lemma,we propose an iterative algorithm based on the idea of Greedy algorithm.

Lemma 1.There exist two kinds of necessary allocated conditions to achieve the optimal solution to problem(30).

•The first necessary condition:the throughput of each group equals and communication energyconstraint satisfies

•The second necessary condition:the allocated energy to the group with the minimum throughput reaches the maximum allowable available energy related to PT.

Proof.Suppose that there exists a groupiwith the minimum throughputUi=Uminand a groupjwith the higher throughputUj >Umin,where the throughput of groupkis denoted asUk=τkRk.

• WhenEiis quite limited,and the maximum transmit power satisfiesEi/τi;therefore,Riis monotone increasing with respect toEi.We can improveRiuntilUi=Ujby increasingEiand decreasingEj.

Additionally,if the total communication energy constraint(30d)is not tight,we can achieve a better performance by increasing energy proportionally for all groups to improve the overall throughput until

• WhenEiis large enough,the maximum transmit power satisfiesand the minimum group throughputUireaches an allowable maximum.

Then,we only can do is to optimize the performance of other groups to guarantee overall fairness.

Thus,lemma 1 is proved.

To maximize the minimum group throughput,we can provide more energy for the group with the minimum rate,while the energy of the group with the maximum rate is reduced.The allocation process is repeated until the optimal solution appears according to the lemma 1.

Accordingly,the intergroup power allocation algorithm is derived,shown in alogrithm 2.

?

Remark 1.When the energy allocated to the group with minimum throughput reaches the allowable maximum and the second necessary condition in lemma 1 is satisfied,we can obtain the optimal solution to(30).To improve the system coverage performance and guarantee inter-group fairness,we should continue to reallocate the rest of energy to other groups.

Remark 2.Clearly,algorithm 2 can converge to the optimal solution due to the limited optimization space.However,the step size δE(j)has a marked effect on the convergence of algorithm 2,which should be sufficiently small or variable.Thus,we choose a variable step size that satisfiesand

3.2.3 Transmission Duration Assignment

When the transmit powerPis given,the transmission duration allocation problem can be expressed as

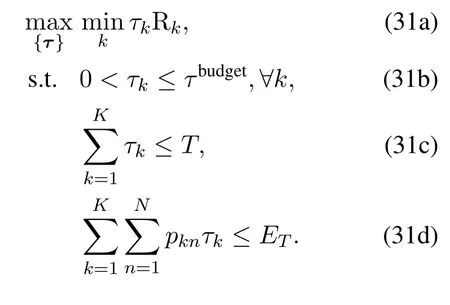
For the convex problem,we can updateτto improve coverage performance.Similar to lemma 1,whenτbudgetis unlimited,the optimal solution should meet the following criteria.

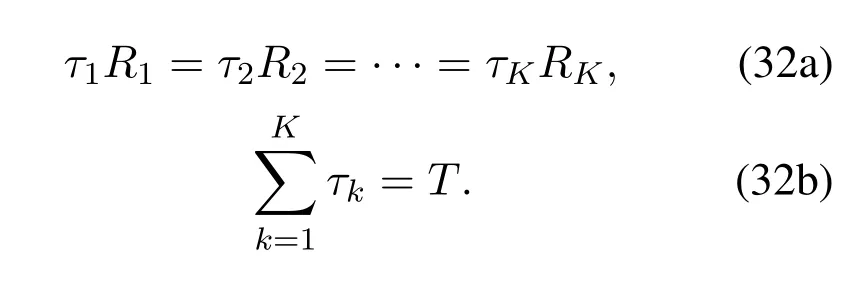
Considering the limited transmission duration budget,we suppose that all groups are sorted byRkin ascending order;thus,the feasible solutionto(32)satisfies

Then,the following transimission durantion assignment rules are applied.

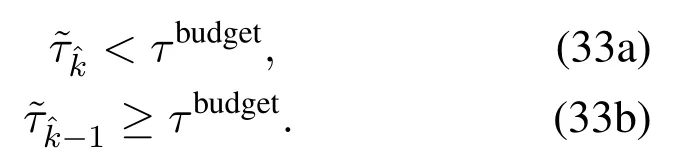
We can reassign{τk}for groups that satisfyk >based on the idea of lemma 1,until the transmission duration conditionholds.Then,the optimum allocation of transmission duration is achieved.

According to the above analysis,we develop an iterative algorithm to solve the original problem (14),as shown in algorithm 3,where the transmit power and transmission duration are updated in turn until it converges.

Notably,the proposed solution is suboptimal due to the nonconvexity.

?

Remark 3.The numbers of iterations are highly related to the values of PT,and τbudget.For example,when the values of PT and τbudget are small enough,we can obtain the optimal solution by one iteration.Thus,the power should be considered in the selection of τbudget.

IV.SIMULATION RESULTS AND DISCUSSIONS

In this section,we evaluate the proposed solution and the impact of various parameters on the coastal coverage performance by simulation.We assume that the ships are randomly deployed in the blind zones within a rectangle sea area and divided into 5 groups each with 4 ships.Without loss of generality,the grouping boundary is perpendicular to the coastline.The system topology and user grouping are shown in figure3.To save propulsion energy,the UAV flies in a straight line at a fixed altitude ofhU=500m and hovers in turn to serve each group following the locations 1 of the UAV in figure3.

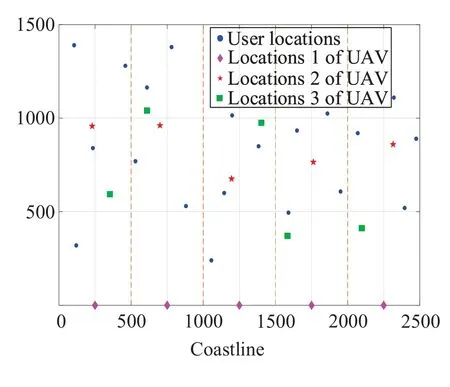
Figure3.System topology for simulation with different hovering locations.

If not otherwise specified,the simulation parameters are set as follows:the communication energyETof the UAV ranges from 40J to 120J,the peak transmit power of the UAV isPT=0.8W,the total transmission duration isT=120s,and the transmission duration budget isτbudget=27.5s.The noise power isσ2N=−107dBm.We set the channel parameters as follows:f=2GHz,c=3×108m/s,a=5.0188,b=0.3511 and(ηLOS,ηNLOS)=(0.1,21),as the maritime propagation environment is similar to suburban environment due to lack of scatterers.Additionally,the number of Monte Carlo simulations for the achievable ergodic rate is 10,000.

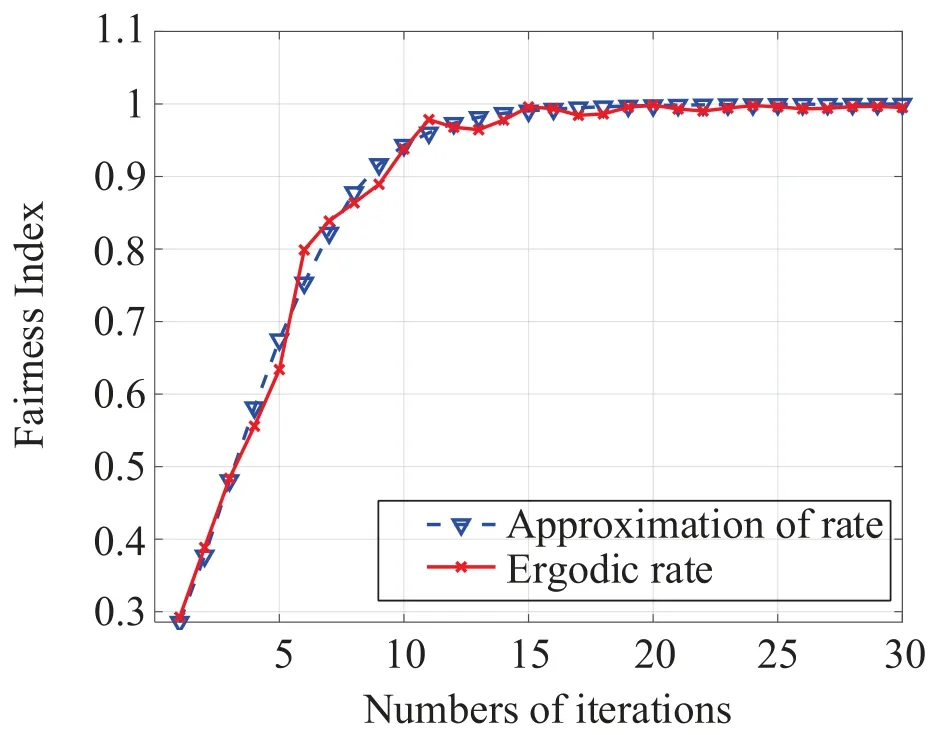
Figure4.Comparison of fairness with different numbers of iterations.

To prove the validity of introducing the approximation of the achievable ergodic rate,we select the Jain’s fairness index as fairness guidance to quantize the fairness of the achievable ergodic rate and its approximation as follows

Figure4 shows that the max-min fairness index of the achievable ergodic rate approaches 1 when the numbers of iterations increases.Besides,the fairness indexes of the achievable ergodic rate and its approximation are consistent all along.Thus,the intragroup power allocation algorithm with the approximation of rate is feasible,and the solution to problem (19) is available.

To evaluate the convergence of the algorithm,we generate 100 random system topologies for test.Figure5 shows the distribution of numbers of iterations of algorithm 2.One sees that the maximum number of iterations is 50,and that the average numbers of iterations is 27.Considering the impacts of peak transmit power and transmission duration budget on convergence of algorithm 3,we compare the maximum number of iterations with different peak transmit power and duration budget in 100 snapshots.In figure6,it is observed that the numbers of iterations increases with larger optimization space for higherPTandτbudget.Furthermore,the proposed algorithm converges within 13 iterations in all cases.

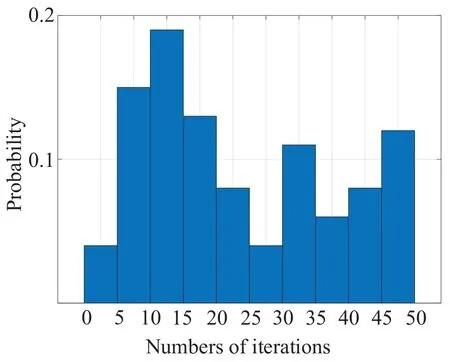
Figure5.Distribution of numbers of iteration of algorithm 2.

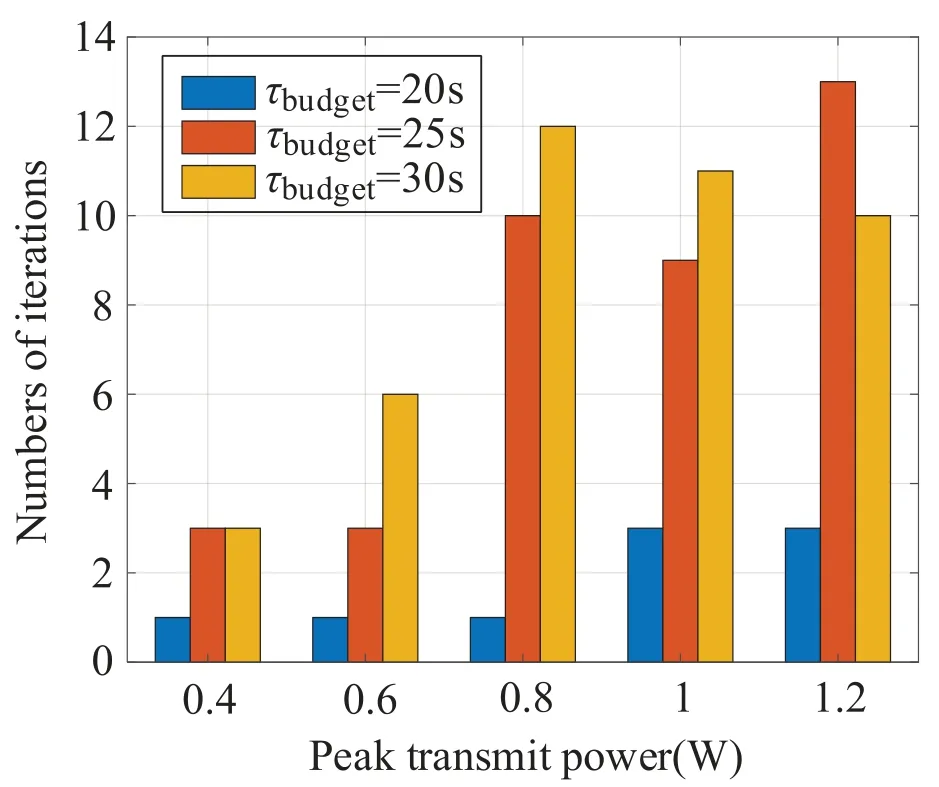
Figure6.Maximum number of iterations with different cases.

To illustrate the superiority of the proposed algorithm,we compare the proposed algorithm with the following algorithms:the algorithm in [12]and [23]with equal transmission duration for each group and the proposed algorithm using OMA instead.The simulation results are shown in figure7.

As we can see,the system’s minimum throughput increases with the communication energy until the available energy reaches the limit due to the peak transmit power constraint.Compared with an OMA system,the proposed algorithm has a significant performance improvement.Also,for NOMA-based system,the algorithm in[12]has the worst performance.Compared with the algorithm in[23],the proposed algorithm shows better performance by introducing intergroup power allocation and transmission duration reassignment.Notably,the minimum throughput of the system is saturated when the communication energy is too high.

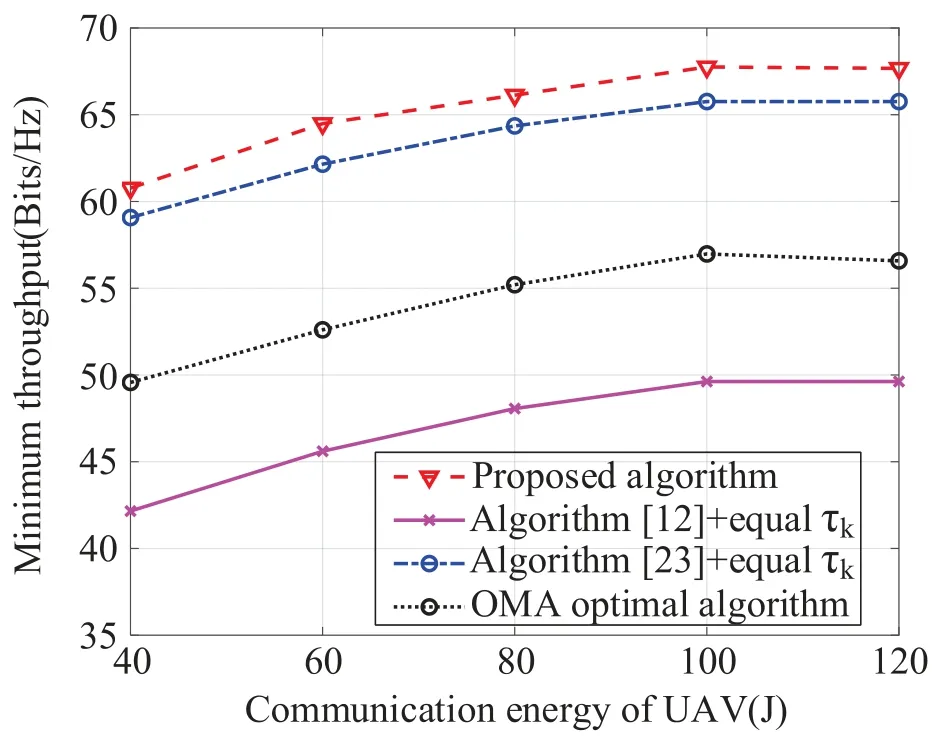
Figure7.Coverage performance by different algorithms.

In figure8,we illustrate the relationship between the total transmission durationTand the coverage performance.The increase inTleads to considerable performance improvement,and the transmission duration of each group is larger.Meanwhile the performance gap with the same increased interval ofTis gradually decreased because the transmit power decreases more quickly with largerT,causing lower throughput.Additionally,whenTis too large,the duration reassignment mainly depends on the duration budget,and minimum throughput reaches saturation.Thus,there exists an optimal total transmission duration related to user rate.

In addition,we compare the coverage performance with different UAV hovering locations,considering that the rotary-wing UAV only transmits at a fixed hovering location.In figure3,there are 3 groups of hovering locations,which represent hovering locations along coastline,hovering locations at the intragroup users’center and random hovering locations for comparison.

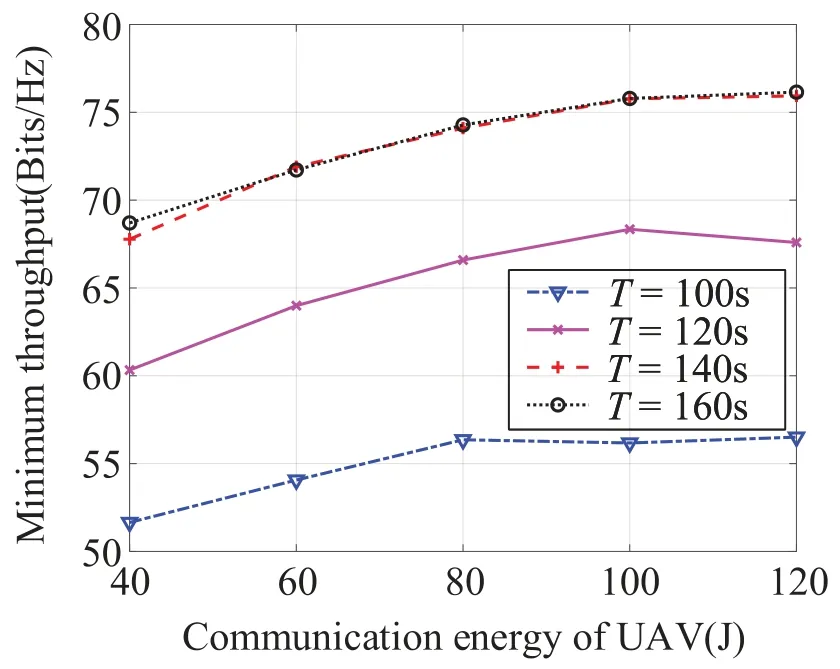
Figure8.Coverage performance with different total transmission durations.

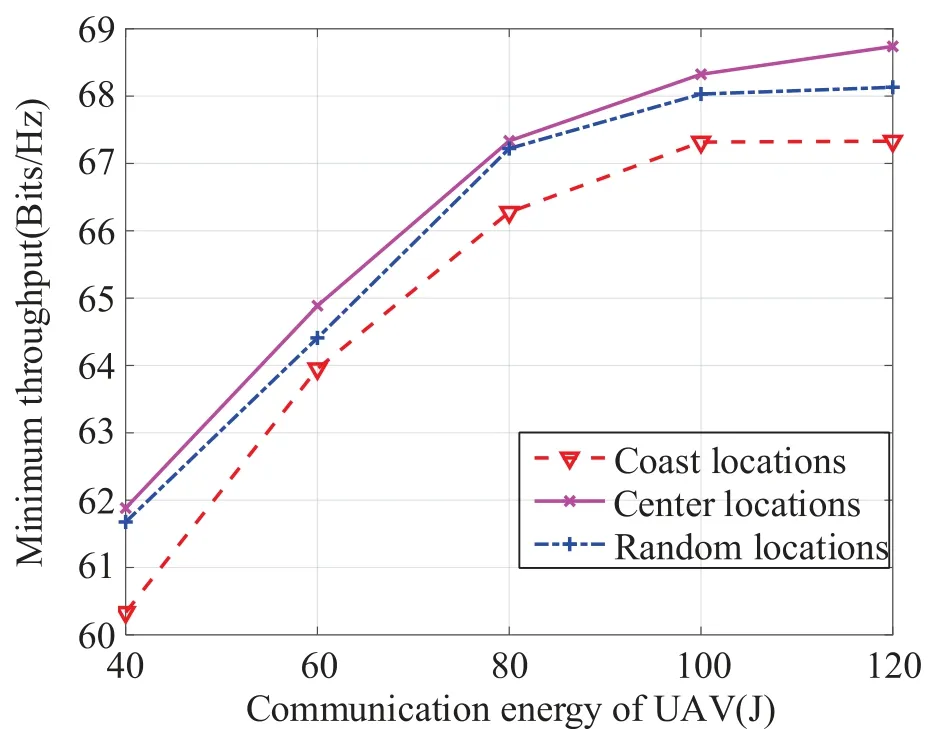
Figure9.Coverage performance with different hovering locations.

Figure10.Coverage performance with different UAV flight altitudes.

In figure9,when the UAV selects the center of each group as hovering location,we can obtain the best coverage performance.In this case,the distance between the UAV and intragroup users is the shortest and the optimal overall channel conditions of each group can be achieved.The hovering locations along the coastline have the worst coverage performance,but the propulsion energy consumption during the flight is reduced,providing service within a larger area.The coverage performance is passable when the UAV hovers randomly,but the flight distance might be long.

In figure10,we verify the impact of UAV altitude on the coverage performance.It is observed that the coverage performance approaches optimum with a UAV altitude of 400m,which is consistent with existing research results.Note that as the UAV altitude increases,the free-space path loss increases,resulting in weaker channel condition.While the probability of LOS propagation increases as well and the channel quality become better[18].Therefore,there exists an optimal UAV altitude that can achieve the best trade-off.

V.CONCLUSION

In this paper,we have developed a NOMA-based maritime UAV communication system to cover blind zones caused by the limitation of SBCN,where a maritime UAV sequentially hovers and provides service for multiple groups of ships on the vast ocean using NOMA.Under the constraints of onboard communication energy and total transmission duration,a max-min optimization problem has been formulated for maritime coverage enhancement by jointly optimizing the transmit power and transmission duration.To solve the non-convex problem,we first decompose it into a transmit power allocation subproblem and a transmission duration assignment subproblem.Simulation results have demonstrated the validity of the proposed solution,and the impact of various parameters on the coverage performance is investigated.

ACKNOWLEDGEMENT

This work was supported in part by National Natural Science Foundation of China (No.61922049,61771286,61941104),the National Key R&D Program of China (2020YFA0711301),the Beijing National Research Center for Information Science and Technology project (BNR2020RC01016),the Nantong Technology Program(JC2019115),and the Beijing Innovation Center for Future Chip.