Guarding Legal Communication with Smart Jammer:Stackelberg Game Based Power Control Analysis

Zhe Su,Nan Qi,*,Yongjie Yan,Zhiyong Du,Jiaxin Chen,Zhibin Feng,Qihui Wu

1 College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

2 State Key Laboratory of Air Traffic Management System and Technology,Nanjing 210014,China

3 28th Research Institute of China Electronics Technology Group Corporation,Nanjing 210007,China

4 College of Information and Communication,National University of Defense Technology,Changsha 430010,China

5 College of Communications Engineering,Army Engineering University of PLA,Nanjing 210000,China

Abstract:This paper investigates a power control problem in a jamming system,where a separate smart jammer is deployed to ensure the communication security of the legal user.However,due to power leakage,the smart jammer may incur unintentional interference to legal users.The key is how to suppress illegal communication while limit the negative impact on legal user.A jamming counter measure Stackelberg game is formulated to model the jamming power control dynamic of the system.The smart jammer acts as a leader to sense and interfere illegal communications of the illegal user,while the illegal user acts as a follower.In the game,the impact of uncertain channel information is taken into account.According to whether illegal user considers the uncertain channel information,we investigate two scenarios,namely,illegal user can obtain statistical distribution and accurate information of interference channel gain and its own cost,respectively.This work not only proposes a jamming counter measure iterative algorithm to update parameters,but also gives two solutions to obtain the Stackelberg equilibrium (SE).The power convergence behaviours under two scenarios are analyzed and compared.Additionally,brute force is used to verify the accuracy of the SE value further.

Keywords:power control;jamming communication systems;Stackelberg game

I.INTRODUCTION

Due to the broadcast nature of the wireless communication environment,wireless communication systems are vulnerable to malicious attacks,such as the cybercriminal activities,information leakage and the active jamming for disrupting legal communication transmissions[1].Also,with the development of electronic attack technology,wireless communication systems are faced with increasingly worse electromagnetic environment.To ensure the reliable transmission of wireless communication,suppressing the communication of the illegal user is crucial.Therefore,the jamming problem of illegal user research is of essential significance.

Jamming problems have attracted attentions from many researchers.Game theory[2–7]has been widely invoked for modeling and analyzing the relationship between the participants.In[8],the authors analyzed the effect of dynamically changing traffic on jamming games for power controlled medium access.In [9],the authors investigated the transmission costs for both the transmitter and jammer based on the non-zero-sum game.In[10],the authors mainly considered the cases with one or two jammers.How the number of jammers impacts the transmission game had been studied.Based on a zero-sum mutual information game,[11]investigated the behavior of two users and one jammer in an AWGN channel.It should be note that most current research works [12]in the jamming field ignore the problem of smart jammer power leakage.In a spectrum shortage environment,a higher jamming power yields a larger impact on illegal user;on the other hand,due to signal leakage,the jammer may affect the legal user on the same channel.

In this study,based on the Stackelberg game,a novel illegal user suppression method is proposed.We deploy a separate smart jammer rather than increasing the legal user’s transmission power to suppress the illegal user.It has the following advantages:1)the signal of legal user carries important information and thus increasing its power has the risk of information leakage;2) the transmission power of a universal transmitter has limited power,which is not suitable for jamming.

To solve the above challenge of how to balance the jamming impact on the illegal user and the negative impact on the legal user,the jamming counter measure Stackelberg game is formulated.The separate smart jammer can appropriately optimize the jamming power according to the practical communication scenarios of the legal user and illegal user,achieving fair trade-off between the jamming effect and transmission cost on the premise of protecting the legal user’s communication.With the influence of the smart jammer,the illegal user has to passively adjust its power suppression to survive.The smart jammer acts as the leader and takes actions first,whereas the illegal user acts as a follower [13–15].Based on the duality optimization theory[16],optimal strategies for both the smart jammer and illegal user are derived.

Note that some works [17–20]have considered the Stackelberg game in the anti-jamming problem.In comparing with the previous work,the main differences of this paper are:1) this paper investigates the jamming problem.Jamming problem mainly focuses on the maximization of smart jammer’s utility.Whereas the anti-jamming problem concerns the maximization of legal user’s utility;2)based on the different sensing abilities of an illegal user,the two solutions are given to acquire the SE.In scenario 1,the optimal power analytical solution of an illegal user is difficult to obtain.So,the bisection method is introduced.Moreover,the SE of the two solutions are compared.

The main contributions of this paper are given as follows:

• A novel jamming approach is proposed to enhance the communication security of the legal user.In this method,a separate smart jammer is deployed to suppress the illegal user.

• The jamming counter measure Stackelberg game is formulated to describe the relationship between the smart jammer and illegal user.In addition,jamming counter measure iterative algorithm is proposed to update transmission power of illegal user and smart jammer.

• According to whether illegal user considers channel information uncertainty,this paper studies two scenarios,namely,illegal user can obtain statistical distribution and accurate information of interference channel gain and its own cost,respectively.Furthermore,we give two solutions:(1)combining jamming counter measure iterative algorithm and bisection method to obtain the SE;(2)deriving analytical solution,and use jamming counter measure iterative algorithm to obtain the SE.

• The existence and uniqueness of the SE are theoretically proved.Moreover,the experimental results and analysis of power convergence,the impact of jammer cost on the utility are shown.Meanwhile,the brute force method is used to verify the accuracy of SE value.In addition,we also compare the SE with the NE to verify the superiority of the proposed game.

The rest of this paper is organized as follows.In Section II,the system model is described.In Section III,the proposed game model,the SE analysis and power control algorithm are presented.The experimental results and discussions are shown in Section IV.The conclusion is drawn in Section V.

Related notations are shown in Table1.

II.SYSTEM MODEL

As shown in Figure1,the communication system consists of one legal transmitter-receiver,one smart jammer and one illegal user.We assume that both the smart jammer and illegal user can sense each other’s power so that both sides can make strategies.The separate smart jammer is deployed to suppress the illegal user(The smart jammer can quickly learn the illegal user’s transmission power by using physical carrier sensing and location knowledge[17]).The advantagesare as follows:1) the legal transmitter carries important information and thus may cause the problem of information leakage,2)the transmitter in the communication pair cannot transmit with high power due to the power limitation of the device itself.As a result,it is unreasonable to directly increase the power of the legal transmitter to jam illegal user.Besides,owing to the legal user is within the radiation range of the smart jammer’s antenna side lobe,it is also unintentionally affected by the power leakage of the smart jammer.

Table1.Notations.

Although raising the power of smart jammer can effectively improve the suppression impact,it is impractical to increase the power as much as possible.The main reason is that the raised power of the smart jammer leads to an increase in the transmission cost and degrade legal user’s communication.

In this paper,the utility functions of illegal user and smart jammer are given,based on the maximum transmission rate,which is one of the critical technical indexes of the communication transmission system.Besides,due to the transmission cost is also a nonnegligible element,the utility is designed as a tradeoff between the maximum transmission rate and the transmission cost.

Figure1.Suppressing illegal user’s malicious jamming via the smart jammer.

2.1 Utility of the Smart Jammer

For the smart jammer,the channel information uncertainty[21]is described by the joint probability distribution because it can only obtain the statistical distributionσu(αl,Ek)of the illegal user’s channel gainαland its own costEk.To intentionally maximize its interference utility after sensing the transmission power of the illegal user,the utility function of the smart jammer can be defined as

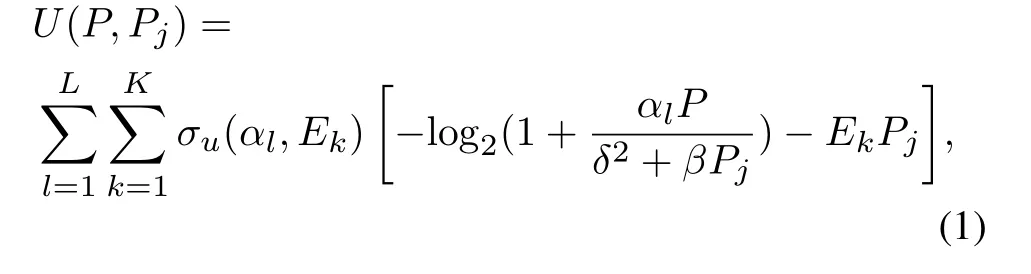
whereσu(αl,Ek),αl,δ,β,Ek,P,andPjcan be referred to Table1.

Based on the random channel,the channel states of the smart jammer are random but finite.We assume that the channel gainαof the illegal user hasLstates in total,defined asα1,...,αl,...,αL,and probabilities ofLstates areϕ1,...,ϕl,...,ϕL,respectively.The transmission costEof the smart jammer hasKstates in total,defined asE1,...,Ek,...,EK,and probability ofKstates areτ1,...,τk,...,τK,respectively.The joint probability distribution of the illegal user’s channel gainαand the transmission costEisσu(αl,Ek),andFurthermore,ϕlandτksatisfyrespectively.

2.2 Utility of the Illegal User in Scenario 1

For the illegal user in scenario 1,the channel information uncertainty is described by the statistical distributionσv(βq,Ct) of the smart jammer’s interference channel gainβqand its own costCt.Due to the limitation of the transmission cost,it is unreasonable for the illegal user to increase the transmission power as much as possible.We consider the trade-off between the illegal user’s throughput after normalization on the channel bandwidth and transmission cost as transmission payoff.Thus,the utility function of the illegal user is

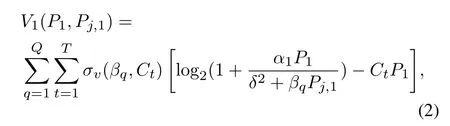
whereP1,Pj,1,σv(βq,Ct),α1,βq,andCtcan be referred to Table1.

Based on the random channel,the channel states of the illegal user are random but finite.We assume that the interference channel gainβhasQstates in total,defined asβ1,...,βq,...,βQ,and probabilities ofQstates areψ1,...,ψq,...,ψQ,respectively.In a similar way,the transmission costCof illegal user hasTstates in total,defined asC1,...,Ct,...,CT,and probabilities ofTstates areφ1,...,φt,...,φT.The joint probability distribution of the interference channel gainβand the transmission costCisσv(βq,Ct),andFurthermore,ψqandφtsatisfy respectively.(Note:the interference channel gainβand the transmission costCrepresent illegal user based on of the channel information uncertainty.)

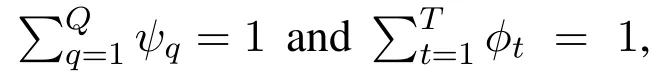
2.3 Utility of the Illegal User in Scenario 2

In scenario 2,the channel information uncertainty is not considered.We assume that illegal user has stronger sense ability and can obtain accurate information of the smart jammer’s interference channel gainβand its own costC.

For the illegal user in scenario 2,the utility function of an illegal user without considering the channel information uncertainty is

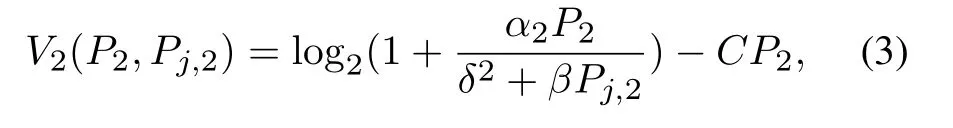
whereP2,C,α2,andPj,2can be referred to Table1.

III.STACKELBERG GAME BASED SOLUTION

A jamming counter measure Stackelberg game is formulated to model and analyze the problem of how to balance the jamming effect of the illegal user and the performance of the legal user.With the influence of the smart jammer,the illegal user has to passively adjust its power suppression to survive.It is assumed that the smart jammer acts as a leader and releases jamming signal first,while the illegal user acts as a follower.

The objective function and constraint of the smart jammer are

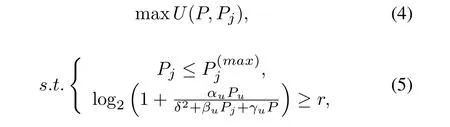
Then,Eq.(5)can express in the following

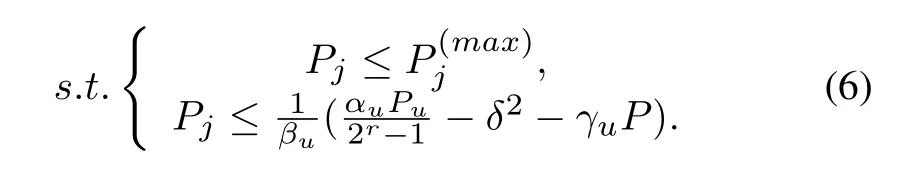
According to Eq.(6),the simultaneous constraints can be acquired as

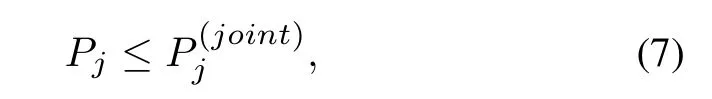
3.1 Optimal Power Control Soluton(Scenario 1)

The objective function and constraint of the illegal user are

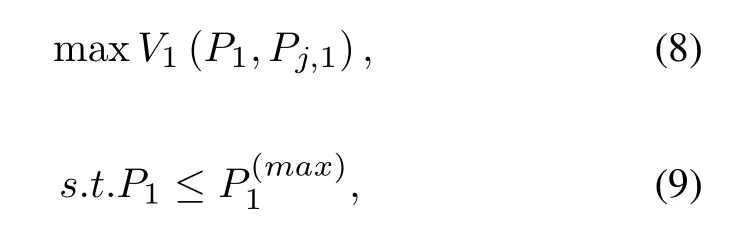
wherecan be referred to Table1.

The utility function Eq.(2) is a concave function when taking the second partial derivative ofP1,since

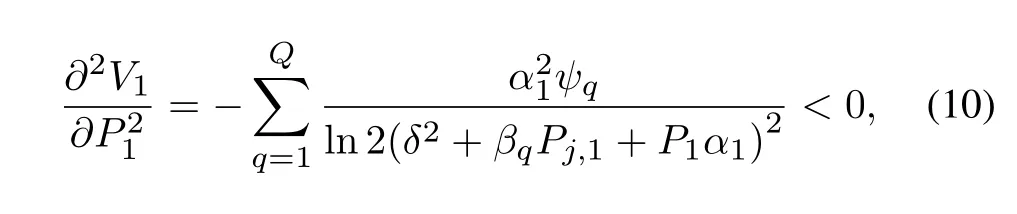
whereψqcan be referred to Table1.

Based on the dual optimization theory,first,the nonnegative dual variableλ1is introduced,and the Lagrangian function composed of Eq.(8)and Eq.(9)is

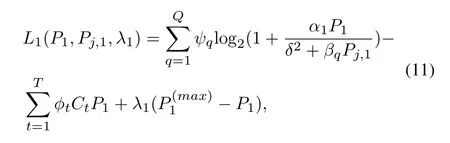
whereφt,λ1can be referred to Table1.

Then,the KKT condition shall be satisfied,i.e.,

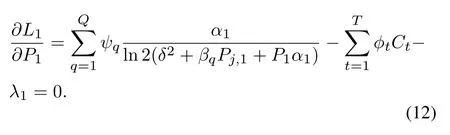
Utility function Eq.(1)is a concave function about transmission power of smart jammer.The nonnegative dual variableµ1is introduced,and the Lagrangian function is

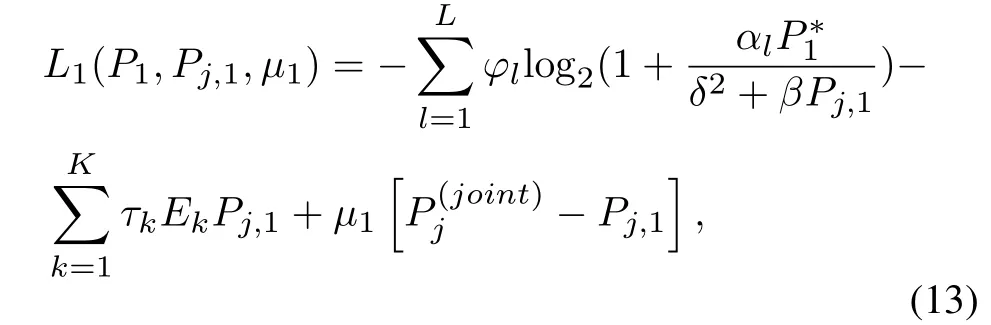
whereτk,µ1,andϕlcan be referred to Table1.

Based on the dual optimization theory,the KKT condition can be applied to the solve the above problem,we let

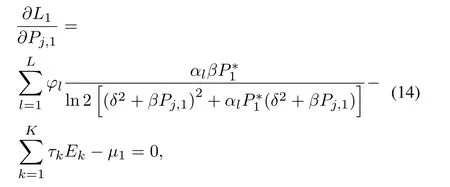
the optimal powerP∗j,1of smart jammer can be obtained by the bisection method.

3.2 Optimal Power Control Solution(Scenario 2)

In this paper,we also consider another scenario.In comparing with scenario 1,the illegal user in scenario 2 has a stronger sensing ability,which can sense the precise value of the interference channel gainβand its own transmission costC.So,the utility of illegal user can be simplified as Eq.(3).In addition,the analytical solutions of illegal user and smart jammer are obtained.

The objective function and constraint are:

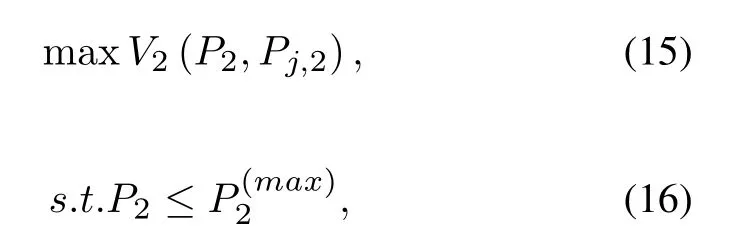
wherecan be referred to Table1.

Proposition 1.When the transmission power of the smart jammer is given,the optimal power of the illegal user is

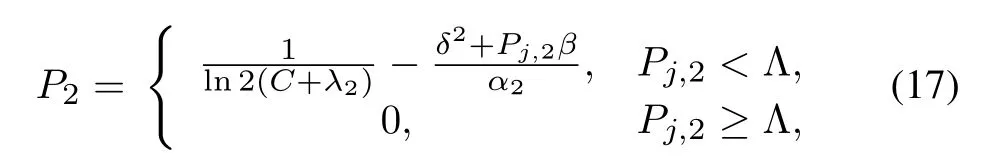
where λ2can be referred to Table1,andΛis

The King45 himself, old as he was, could not help watching her, and telling the Queen softly that it was a long time since he had seen so beautiful and lovely a creature.

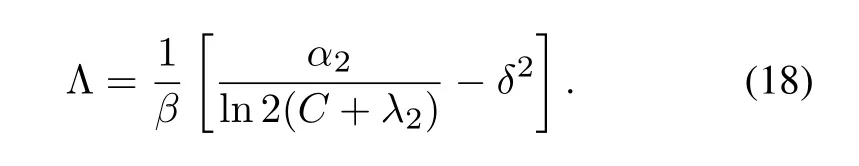
Proof.We take the second partial derivatives Eq.(3)with respect toP2,and obtain that

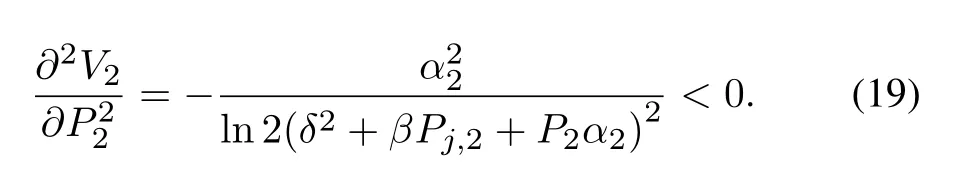
By introducing non-negative dual variableλ2,the Lagrangian function is

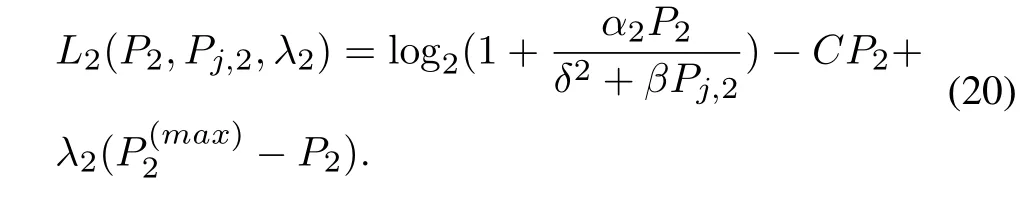
The following KKT condition shall be satisfied

The optimal transmission power of illegal user can be acquired with the sub-gradient method.

Proposition 2.The optimal transmission power of the smart jammer is

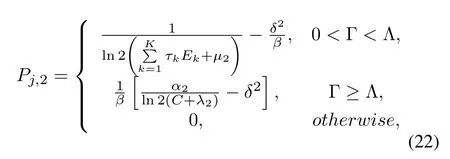
whereΓis given by

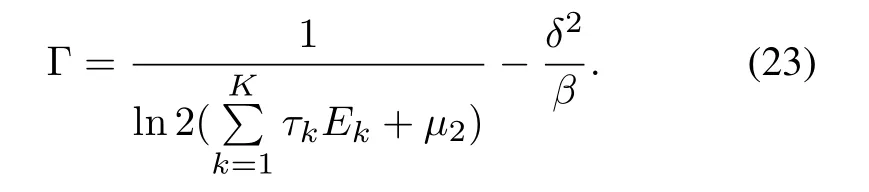
Proof.By substituting Eq.(17)into Eq.(1),the utility of the smart jammer is

whereu1andu2are respectively given as

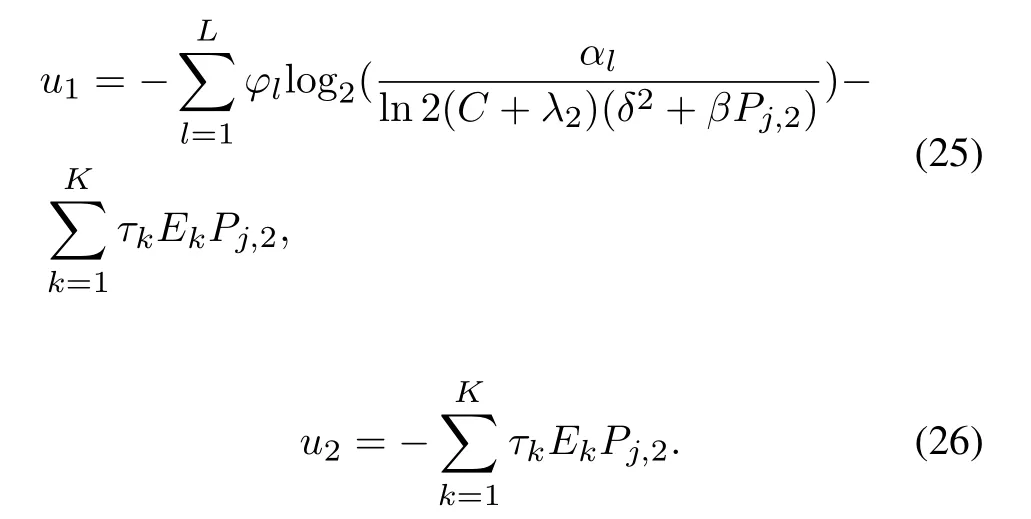
When the conditionPj,2≥Λ is satisfied,the utility of the smart jammer is a liner function aboutPj,2.When the conditionPj,2<Λ is satisfied,the utility of the smart jammer is a concave function about transmission powerPj,2.

First,the non-negative dual variableµ2is introduced,and the Lagrangian function is

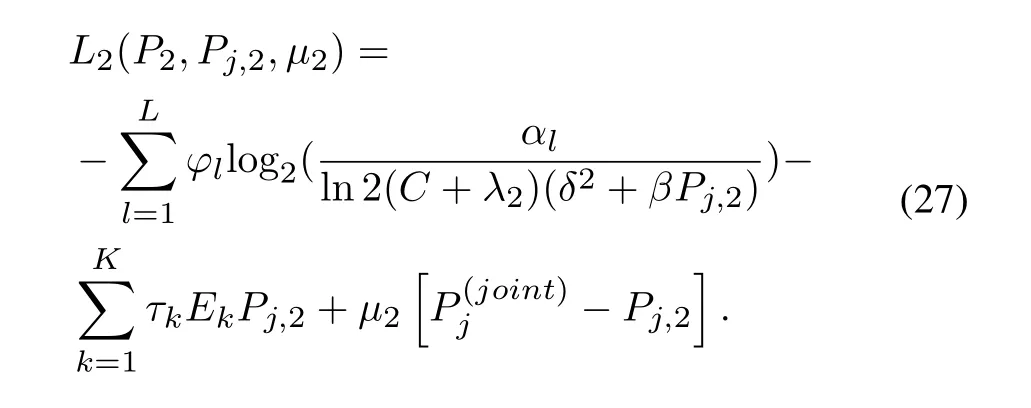
It can be noted that Eq.(25)is a concave optimization problem.The KKT condition can be applied to solve above problem,we let

Further,the optimal power of the smart jammer can be obtained as

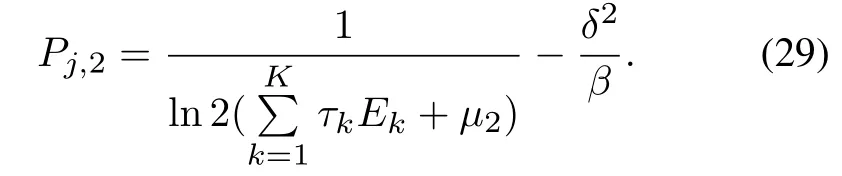
In order to analyze the maximum value of Eq.(24),we consider the following cases:

1)Λ≤0:U(P2,Pj,2)achieves its maximum value whenPj,2=0.

2)Λ>0,Γ≤0:U(P2,Pj,2)achieves its maximum value whenPj,2=0.

3) Λ>0,0<Γ<Λ:U(P2,Pj,2) achieves its maximum value whenPj,2=Γ.

4) Λ>0,Γ≥Λ:U(P2,Pj,2) achieves its maximum value whenPj,2=Λ.

?

?

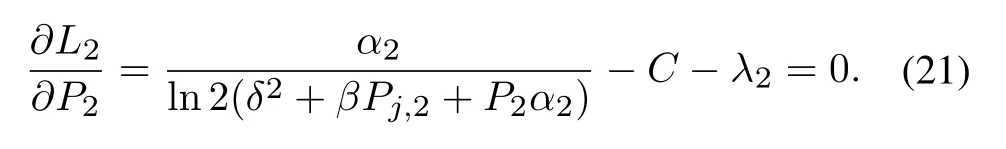
3.3 Jamming Counter Measure Iterative Algorithm

Based on the sub-gradient method,the jamming counter measure iterative algorithm is proposed to update system parameters of scenarios 1 and 2.The specific algorithm is shown in Algorithm 1 and Algorithm 2.

3.4 Analysis of Existence and Uniqueness of the SE

Since the proof process for scenarios 1 and 2 are the similar,we take scenario 2 as an example.The SE can be defined as follows.

Definition 1.The illegal user and smart jammerjamming counter measure Stackelberg game when the following conditions hold

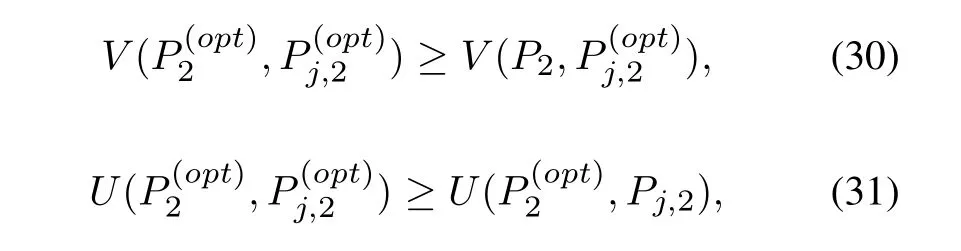
where P2and Pj,2represent any optional strategies.

Theorem 1.The SE exists and is unique for the jamming counter measure Stackelberg game.

Proof.Proof of existence:based on the analysis in Section 3.2,we can find that the utility function of the illegal user is concave with respect toP2,which has been proved in [22];proof of uniqueness:given the smart jammer powerPj,2,the utility function of the illegal user is concave with respect toP2.So,there exists a unique best response.According to Eq.(21),there exists a unique best response for the smart jammer.Therefore,the SE is unique.

IV.EXPERIMENTAL RESULTS AND ANALYSIS

In this section,experimental results and analysis are presented.In Section 4.1,the convergence of the smart jammer power and the illegal user power are analyzed and compared.Also,the brute force method is used to verify whether the value of SE is correct or not.In Section 4.2,the impacts of jammer cost on utility are discussed.In Section 4.3,the smart jammer’s performance of SE and NE are compared under channel information uncertainty.

4.1 Analysis of Power Convergence

The transmission power convergence of scenarios 1 and 2 are shown in Figure2.

For scenario 1,as the convergence iteration executes,illegal user and smart jammer increase transmission power at the same time to maximize their own utilities.After 11 iterations,both sides converge to the SE.

For scenario 2,the smart jammer increases the transmission power to jam the illegal user’s communication.Both sides converge to the unique SE after 7 iterations.In comparing with the scenario 1,the power convergence value of the bisection method is smaller.The reason is that the interference channel gainβin scenario 1 are given larger values.

In this part,the existence and uniqueness of SE in scenarios 1 and 2 are verified.Moreover,the brute force method is used to verify whether the value of SE is correct or not.Considering that the verification process of scenarios 1 and 2 are the similar,we take scenario 2 as an example.As shown in Figure2,the transmission power value obtained by brute force is the same as the value(P2−Alg2:2.5895W,Pj,2−Alg2:4.4391W)of SE in scenario 2.Therefore,the converged power value is accurate.

Figure2.Transmission power convergence analysis.

4.2 The Impact of Jammer Cost on Utility

Figure3 shows the impacts of smart jammer cost on the utility in scenarios 1 and 2,for which we can obtain a similar conclusion.Specifically,the utility of the illegal user increases with the transmission cost of the jammer;on the contrary,the utility of the jammer decreases.The reason is that the utility function of the smart jammer is a trade-off between the illegal user’s throughput and transmission cost.The increase in the cost of the jammer indicates a reduction in jamming effect to illegal user.

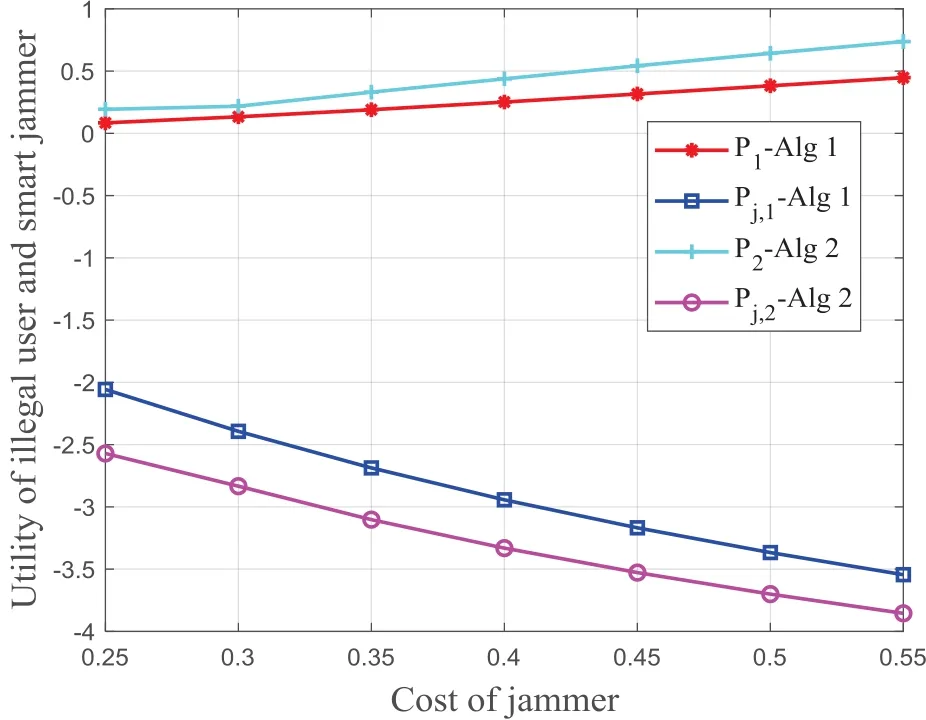
Figure3.The impact of jammer cost on the utility.

4.3 The Comparison of SE and NE

In this part,the fluctuation coefficient is introduced to discuss its impact on utility.The fluctuation coefficient represents the degree of the observed value devi-ating from the practical value.The fluctuation coefficient is larger,the degree of deviation is more serious.

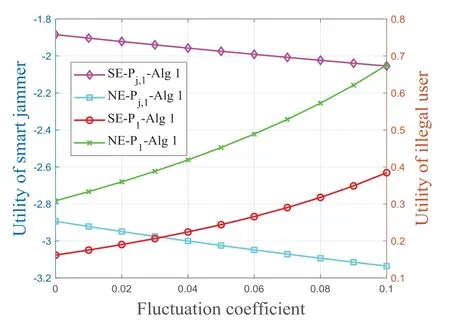
Figure4.Smart jammer’s performance comparison of SE and NE in scenario 1.

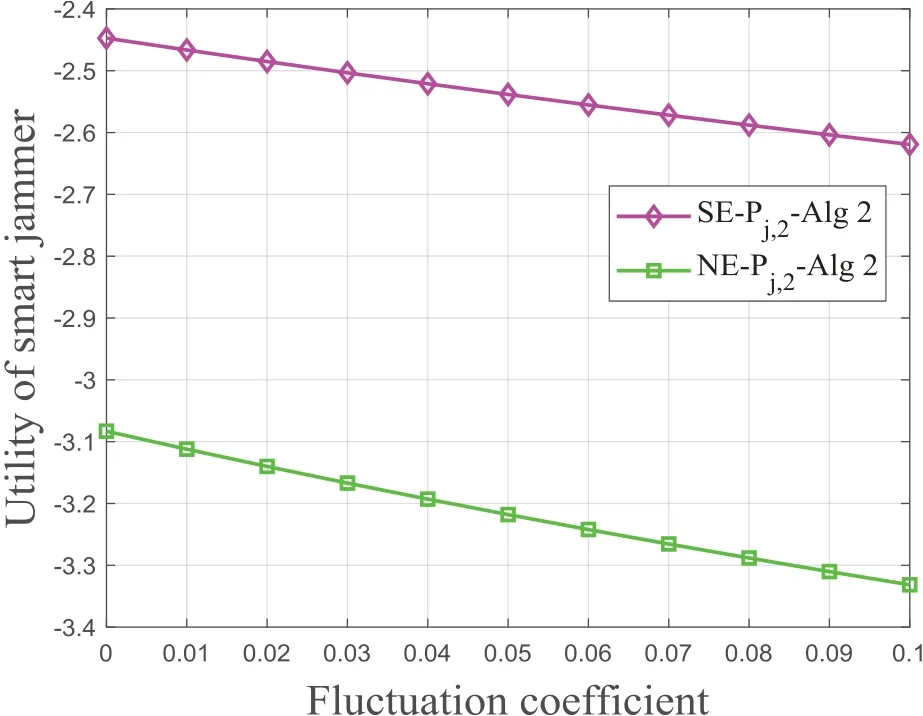
Figure5.Smart jammer’s performance comparison of SE and NE in scenario 2.

The comparison of SE and NE in scenario 1 is shown in Figure4.It is clear to find the smart jammer’s utility decreases with the fluctuation coefficient.For the smart jammer,due to the rise of the fluctuation coefficient,the deviation degree between the channel gain observed by the jammer and the practical channel transmission gain of the illegal user is higher,which results in the reduction of the effectiveness of the smart jammer.For the illegal user,jamming impact of smart jammer decreases due to the increase of fluctuation coefficient,which leads to the improvement of the utility of an illegal user.

As shown in Figure5,we can also get similar conclusions about the changing trend of the utility functions of illegal user and smart jammer.

Moreover,in Figure4 and Figure5,based on the uncertain channel information,we compare the utilities of SE and NE.For the smart jammer,the utility of the SE is higher than the utility of the NE.The smart jammer learns illegal user’s strategies and makes corresponding strategies rapidly.NE is a non-hierarchical game equilibrium,so its utility is lower than SE.This further illustrates that the superiority of the jamming counter measure iterative algorithm.

V.CONCLUSION

In this paper,a novel jamming approach was proposed.A separate smart jammer was deployed to suppress illegal communication.Based on the channel information uncertainty,jamming counter measure Stackelberg game was formulated to model the jamming power combating between the illegal user and smart jammer.A jamming counter measure iterative algorithm was proposed.According to whether illegal user considered game channel information uncertainty,the two solutions were given.Moreover,the existence and uniqueness of SE were proved theoretically.Simulation results and power convergence analysis in scenarios 1 and 2 were presented.Furthermore,the brute force method is used to verify the accuracy of the SE value.The impacts of jammer cost on the utility in scenarios 1 and 2 were shown.Meanwhile,under the uncertain channel information,the utilities of SE and NE in two different scenarios were also compared.

ACKNOWLEDGEMENT

This work was supported in part by National Key R&D Program of China under Grant 2018YFB1800800,by National NSF of China under Grant 61601490,61801218,61827801,61631020,and by the open research fund of Key Laboratory of Dynamic Cognitive System of Electromagnetic Spectrum Space(Nanjing Univ.Aeronaut.Astronaut.) (No.KF20181913),in part by State Key Laboratory of Air Traffic Management System and Technology under SKLATM201808,in part by the Natural Science Foundation of Jiangsu Province under Grant BK20180420,BK20180424,and by the Open Foundation for Graduate Innovation of NUAA(Grant NO.kfjj20190417).