Energy-Efficient Power Allocation for IoT Devices in CR-NOMA Networks

Guangfu Wu,Wenyi Zheng,Yun Li,*,Mengyuan Zhou

1 School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications Chongqing,400065,China.

2 Chongqing Key Laboratory of Mobile Communications Technology,Chongqing University of Posts and Telecommunications,400065,China.

Abstract:Non-orthogonal multiple access is a promising technique to meet the harsh requirements for the internet of things devices in cognitive radio networks.To improve the energy efficiency (EE) of the unlicensed secondary users (SU),a power allocation(PA)algorithm with polynomial complexity is investigated.We first establish the feasible range of power consumption ratio using Karush-Kuhn-Tucker optimality conditions to support each SU’s minimum quality of service and the effectiveness of successive interference cancellation.Then,we formulate the EE optimization problem considering the total transmit power requirements which leads to a non-convex fractional programming problem.To efficiently solve the problem,we divide it into an inner-layer and outer-layer optimization sub-problems.The inner-layer optimization which is formulated to maximize the sub-carrier PA coefficients can be transformed into the difference of convex programming by using the first-order Taylor expansion.Based on the solution of the inner-layer optimization sub-problem,the concave-convex fractional programming problem of the outer-layer optimization sub-problem may be converted into the Lagrangian relaxation model employing the Dinkelbach algorithm.Simulation results demonstrate that the proposed algorithm has a faster convergence speed than the simulated annealing algorithm,while the average system EE loss is only less than 2%.

Keywords:cognitive radio-non-orthogonal multiple access (CR-NOMA);power allocation;energy efficiency;internet of things(IoT)

I.INTRODUCTION

The fifth-Generation mobile communication system(5G)introduces massive machine type communication(mMTC) and ultra-reliable and low latency communication (uRLLC) scenarios for the internet of things(IoT) application,as specified by the international telecommunications union-radio communications sector (ITU-R) [1].To align with the above-mentioned requirements of massive IoT,the 3rd Generation Partnership Project (3GPP) sets up the narrow-band IoT(NB-IoT) and long term evolution (LTE)-M standard as part of Release 13 [2].Both of them are known as cellular IoT since they are part of the cellular network.Other appealing non-cellular IoT technologies which provide low power and long-range communications are LoRa[3]and SigFox[4].The rapid development of IoT leads to an explosive increase of diverse wireless devices and the rapid growth of high-rate mobile services [5].However,the spectrum scarcity has become a major bottleneck for the employment of IoT.To further improve the spectrum efficiency (SE),cognitive radio (CR) is a promising technique by enabling the secondary users(SUs)to share the licensed spectrum with the primary user (PU) on the condition that the interference leaked to the PU is acceptable[6].The overlay and underlaying spectrum sharing strategies are widely implemented in CR networks.For overlay strategy,the SUs are required to detect the underutilized licensed spectrum to access,which can avoid collision with the PU.The underlaying strategy has rekindled increasing interest in using the spectrum more efficiently.The key idea of underlaying CR networks is that each SU can transmit simultaneously with PU at the same time and frequency resource by controlling the interference to the primary receiver under a tolerable threshold[7].

Besides CR,non-orthogonal multiple access(NOMA) is another promising technique to enhance system SE and achieve massive connectivity of IoT devices in CR networks by employing the underlaying strategy.NOMA usually utilizes the power domain for multiple access,where different users are served at different power levels depending on the radio channel quality and the successive interference cancellation(SIC)which are employed to distinguish the different transmit signals may eliminate the co-channel interference at the receiver [8].NOMA system can be divided into uplink and downlink systems [9]-[10].The authors in [9]investigated a user pairing in uplink NOMA to achieve the maximum sum-rate with polynomial-time complexity.In [11],a joint user pairing and PA problem was modeled as a mixed-integer programming problem to optimize the achievable sum-rate with the minimum transmission rate constraint of each user.The authors proposed an optimal PA algorithm and a less complex suboptimal clustering method to maximize the total system throughput on both uplink and downlink single antenna NOMA systems[10].

CR-NOMA which is the wireless communication networks employed with NOMA technology has great potential to satisfy the IoT requirements of massive connectivity as it can serve more SUs by sharing the licensed spectrum with PUs.At the same time,energy efficiency (EE) has been taken particular attention to extend very long battery life,especially for energy-limited IoT devices[12].There are many feasible strategies to improve the EE of IoT devices in CR-NOMA networks.One feasible strategy is that the IoT receiver only adopts low complexity detection and demodulation algorithms.Consequently,NOMA is much suitable for uplink CR system,because the secondary Base Station (BS) as IoT receiver is not generally energy-limited,and which may adopt the minimum mean squared error(MMSE)or MMSE and successive interference cancellation (MMSE-SIC) to achieve less digital signal processing delay[13].Another feasible strategy is that the transmit power of IoT devices should be allocated more accurately by invoking advanced power allocation algorithms.

In recent years,the EE-based PA problem has also been widely investigated in NOMA system.In [14],the maximization EE problem for downlink network was studied subject to each user’s minimum required data rate.The EE-based PA problem was considered by exploiting convex relaxation and dual decomposition techniques in downlink NOMA heterogeneous network[15].In[16],resource allocation algorithms for sub-channel assignment and EE dynamic PA in downlink NOMA network were investigated using the Lyapunov optimization method by considering the constraints of the minimum user quality of service(QoS)and the maximum transmit power.In[17],maximizing the lifetime of critical node and minimizing the consumption of the relay node of underwater acoustic sensor networks are the two main conflicting objectives which were met by applying the multi-objective optimization.Firstly,the weighted sum method was applied to transform the above multiobjectives into a single objective.Then the difference convex(DC)algorithm was developed to find a globally optimal solution.The authors in[18]formulated a problem to minimize the energy cost of mobile edge computing(MEC)considering the transmit power and latency constraints.To solve the proposed mixedinteger nonlinear programming problem,a joint Benders decomposition and distributed Dinkelbach algorithm was studied.The Benders decomposition which was performed as an outer loop algorithm separated the original problem into outer and inner-loop subproblem.The inner-loop sub-problem was solved by the distributed Dinkelbach algorithm in a distributed manner.

The EE PA problem also plays a key role in CRNOMA networks.Most current literatures studied the EE PA problem based on downlink system.The adaptive spectrum sharing schemes were studied to improve both the minimum EE in half-duplex mode and the overall EE in full-duplex mode CR networks[19].The authors investigated the PA problem aiming to maximize the number of admitted SUs based on system throughput,considering the interference tolerance threshold of PUs in downlink CR-NOMA networks[20].In[21],the EE optimization problem was explored subject to an individual QoS constraint for each PU in the multi-user and multi-antenna downlink CR-NOMA system.Only a few literatures studied the uplink power allocation algorithm based on EE.The uplink user equipment(UE)group-based scheduling technique was proposed to mitigate the differential Doppler of the IoT devices for low earth orbits(LEO)satellite-based mMTC-NB-IoT system [22].The resource allocation algorithm was studied to maximize the system sum-rate and EE using the iterative waterfilling solution for multi-carrier uplink NOMA system[23].

In summary,current research literatures mainly focus on SE and the interference threshold from the SUs to the PU utilizing underlaying spectrum sharing strategy in CR networks.NOMA is usually employed to enhance the downlink of massive connectivity and system capacity for the traditional enhanced mobile broadband(EMBB)scenario of the mobile communication system.In the IoT environment,massive connectivity,long battery life and high capacity for IoT devices will be supported by mMTC scenario in the near future.For early small capacity NB-IoT application,e.g.,smart meters,the conventional equal fixed or fractional transmit PA strategy which is commonly employed only considered the channel quality of each user cannot meet the requirements for mMTC scenarios [24,25].It is very urgent to investigate the EEbased PA of unlicensed SUs to extend their battery life in uplink underlaying CR-NOMA networks,especially for the high capacity requirement of the IoT devices,e.g.,network intelligence video surveillance system[26].

To meet the requirements of high SE,massive connectivity and low power consumption for IoT devices in CR-NOMA networks,a PA algorithm is investigated to improve the EE of the unlicensed SUs under the constraints of maximum tolerable interference from the licensed PU.The key contributions of this paper can be summarized as follows:

• For the uplink underlaying CR-NOMA networks,the EE-based power allocation problem is formulated with the constraints of the total transmit power,the minimum communication quality,the maximum power consumption ratio,and the SIC effectiveness.

• Based on the convex optimization theory,we establish the feasible range of power consumption ratio that is required to support each SU’s minimum transmit QoS.

• The EE-based power allocation problem may be decomposed into two sub-problems:sub-carrier power allocation sub-problem (inner-layer optimization sub-problem) and power consumption ratio sub-problem (outer-layer optimization subproblem).

• The sub-carrier power allocation sub-problem is solved utilizing the difference of convex(DC) programming to maximize the sub-carrier throughout under the constraints of SUs’the minimum transmit QoS and the effectiveness of SIC receiver.The suboptimal power consumption ratio is solved to maximize the system EE by applying the Dinkelbach algorithm and Lagrange algorithm.

The computational complexity of the proposed algorithms is analyzed and compared with the SA and full search power algorithm (FSPA).The average system energy efficiency(ASEE)and total system throughput performances of the proposed algorithms are evaluated by extensive simulations.Numerical results show that the proposed algorithm has a faster convergence speed than the simulated annealing algorithm,while the average system EE loss is only less than 2%.

The rest of this paper is organized as follows.Section II presents the EE-based system model.In section III,an EE-suboptimal PA algorithm (EEPA) is proposed.Following that the simulation results are presented in section IV.Finally,conclusions are drawn in section V.

II.EE-BASED SYSTEM MODEL

2.1 System Model

In the uplink underlaying CR-NOMA network,as shown in Figure1,the unlicensed multiplexed SUs transmit signals to the secondary BS by sharing the same sub-carrier with a licensed PU simultaneously.We assume that each secondary user(SU)and the secondary BS are equipped with single antenna.The secondary BS not only can estimate the channel gains between the SUs and the secondary BS,but also can estimate the channel gain between the PU and the secondary BS by using the same sub-carrier.

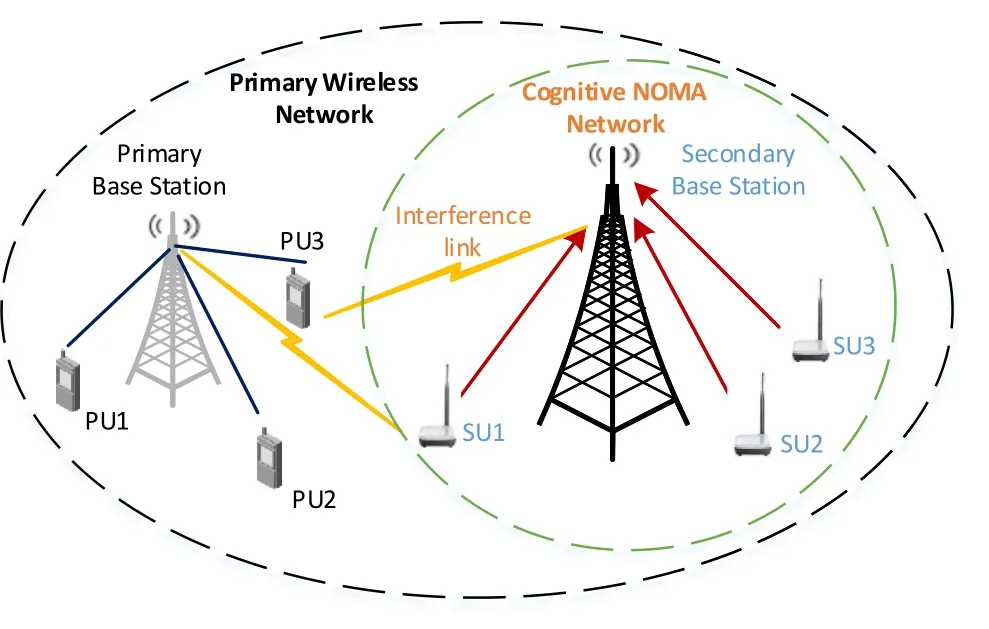
Figure1.The system model of uplink underlaying CRNOMA networks.

Assume that the total bandwidth of the primary BS is divided equally intoMorthogonal sub-carriers,so that the interference between sub-carrier is avoided.We denotemas an index for the sub-carrier according to the corresponding PU wherem ∈{1,2,···,M}andias the index for theith SU wherei ∈{1,2,···,N}.It is assumed thatLSUs multiplex themth PU sub-carrier adopting NOMA technology,whereL≤Lmax≤N,Lmaxis the maximum allowed number of multiplexed SUs on a PU sub-carrier.The transmitted symbol of SUion sub-carriermisxi,m,αi,mis the PA coefficient allocated by the secondary BS for SUion sub-carrierm.PowerPmis the allowed total sub-carrier power allocated to all the multiplexed SUs,then all the actual transmit powerPtof the multiplexed SUs on themth sub-carrier is expressed asThe total received signal at the secondary BS can be expressed as

where,Gi,mis the channel gain on sub-carriermfrom SUito the secondary BS,hmis the channel gain from PUmto the secondary BS which includes both largescale path-loss and small-scale Rayleigh fading,pmis the transmit power of PUm,xmis the transmit symbol of PUi,ni,mis the additive Gaussian white noise(AWGN) with zero mean and varianceσ2.For the sake of simplicity,the AWGN at the secondary BS and the interference coming from PUmcan be expressed together asNm=σ2+|hm|2pm.

Different from the downlink,all signals received at the secondary BS are desired signals,although they may cause multi-user interference.In the downlink,the SIC order is fixed with the ascending order of the channel gains,i.e.,the users with lower channel gains are decoded first and removed.However,in the uplink,the SIC order can be flexible,e.g.,the secondary BS can choose the exact user to decode in an arbitrary order [24].Regardless of that,to apply SIC and decode the signals at the secondary BS efficiently,the PA algorithm should be fully exploited such that the distinctness among various signals can be maintained,and the ascending order of the channel gains have been kept before SIC process.

2.2 Maximum Power Consumption Ratio

It is assumed that the PA algorithm of inter-sub-carrier has been completed using the fix power allocation algorithm [27],and the PA problem of the innersub-carrier is mainly considered in this paper.The signal-to-interference-plus-noise ratio(SINR)may be adopted as a measure of mobile communication quality [28].If the total transmit power allocated isPtot,then the powerPmin a sub-carrier allocated to all the multiple SUs isPm=Ptot/M.

Without loss of generality,all the equivalent channel gains of SUs multiplexed on sub-carriermare arranged in descending order according to the equivalent channel gains:H1,m ≥H2,m ≥··· ≥HL,m.At the secondary BS,the SUs with strong equivalent channel gains can decode the SU signals with weak equivalent channel gains,while the SUs with weak channel gains can only consider the SU signals with strong equivalent channel gains as interference.For the ideal radio channel,the SINR of SUiafter SIC on sub-carriermis performed as

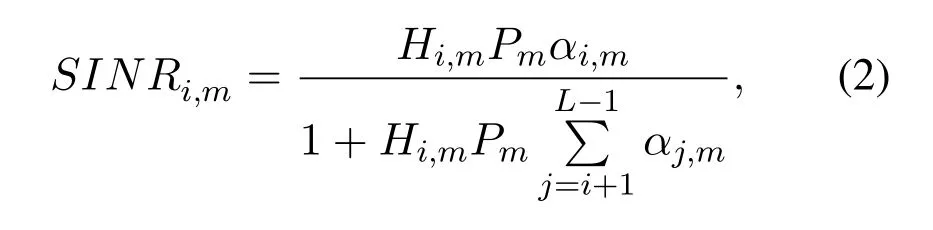
where,Hi,m=Gi,m/Nirepresents the equivalent channel gain of SUion sub-carrierm.

To ensure the QoS of each SU,the SINR of SUimultiplexed on sub-carriermmust be bigger than or equal to the minimumSINRmin,SINRi,m ≥SINRmin,∀i ∈L,m ∈M.Combined with Eq.(2),the corresponding PA coefficientαi,mshould satisfy the minimumSINRminrestriction

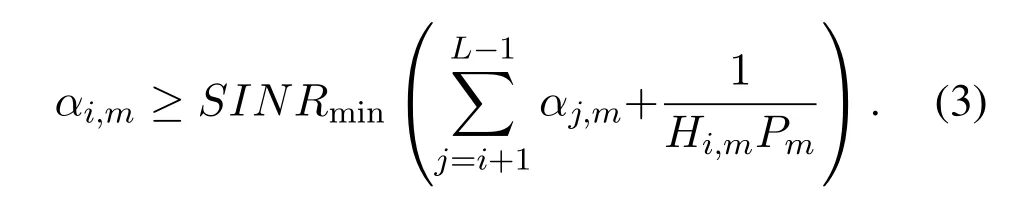
On the other hand,the multiplexed SUs access the licensed PU’s frequency band in underlaying mode,it is necessary to ensure that all the interference generated by multiplexed SUs on sub-carriermis less than or equal to the interference power limitationImof PUm.

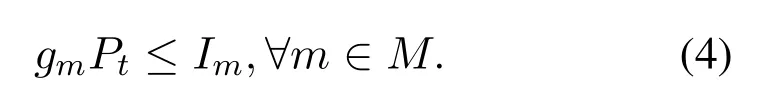
In Eq.(4),gmis the channel gain coefficient from PUmto the secondary BS.

The power consumption ratioθmis defined on subcarriermas the ratio of the actual transmit powerPtto the powerPmwhich is allocated to all the multiplexed SUs.

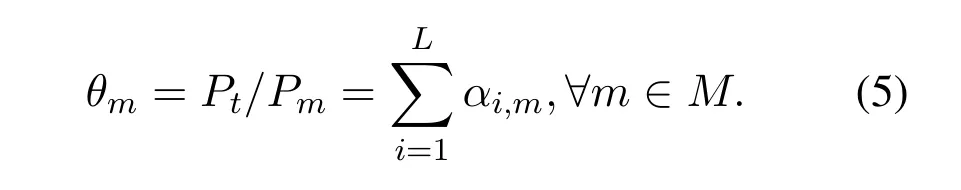
The constant power consumption of circuits including all power dissipated in the circuit of transmitter and receiver blocks is needed to operate each SU,and the actual transmit power for multiplex users is not always been allocated entirely to reduce the interference between each other and keep the effectiveness of SIC receiver.On the other hand,it is impossible to utilize all the allocated power in the shared sub-band,because the user terminals of IoT devices go to sleep as soon as possible to extend the battery life.That is to say thatPtis always less thanPm.Combined with the above definition,we can see that the range of power consumption ratioθmis 0<θm <1.

Substituting (5) into (4),we may further get the maximum power consumption ratio limit given by

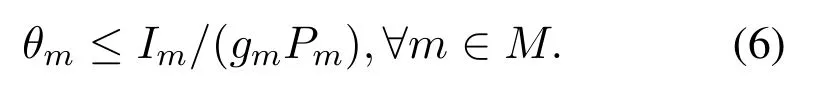
From Eq.(6),we know that the power range allocated to the multiplexed SUs on the sub-carriermmay be narrowed further.

2.3 Problem Formulation

According to Shannon’s capacity formula,the total throughput of sub-carriermis given by where,Bmis the bandwidth of a sub-carrier.

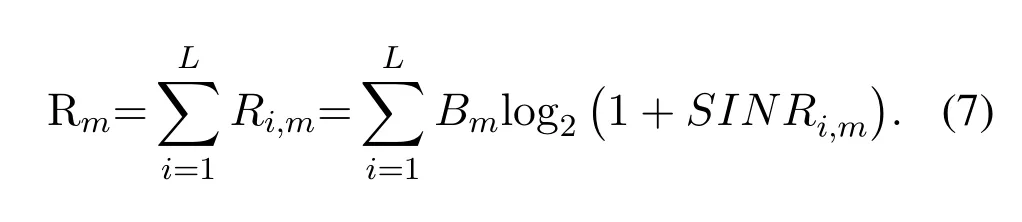
The total system EE is defined as the ratio of the achievable total throughput of the system to the actual power consumption,which can be expressed aswherePcis the constant power consumption of circuits including all power dissipated in the circuit of transmitter and receiver blocks to operate the terminals[29].Therefore,we formulate the total system EE optimization problem as follows

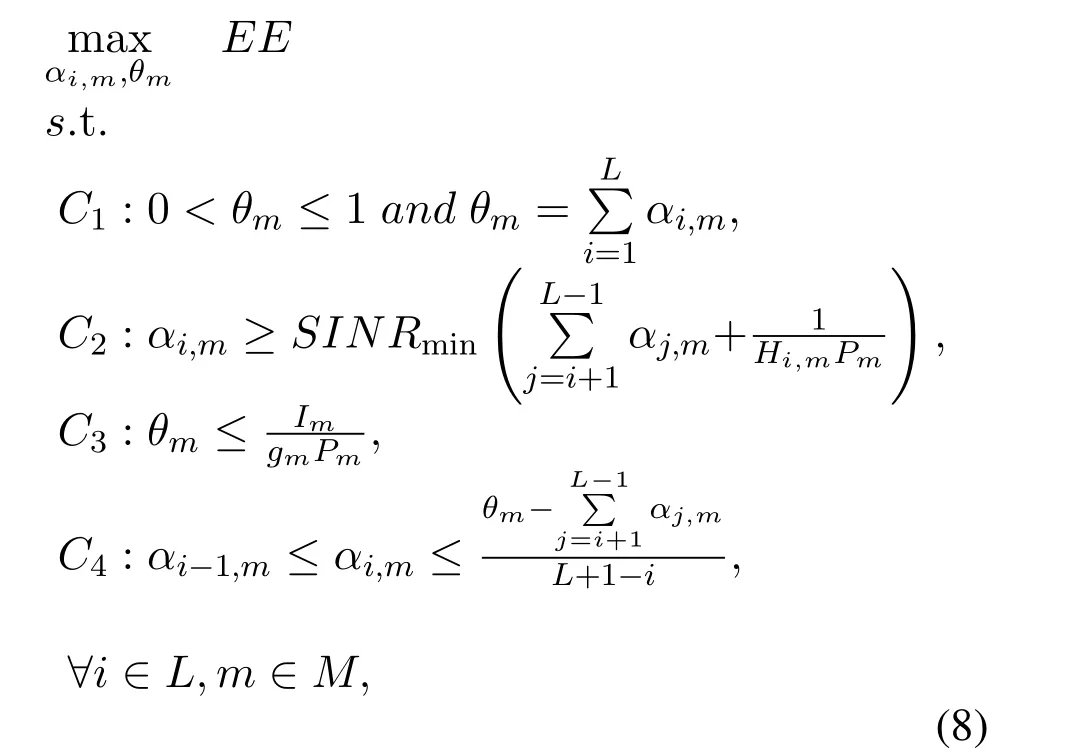
where the constraint conditionC1represents the total transmit power constraint for all SUs,the constraint conditionC2represents the minimum QoS requirement for each SU,the constraint conditionC3represents the maximum power consumption ratio,and the constraint conditionC4can ensure the effectiveness of SIC receiver.

Since this optimization problem is a non-linear fractional programming problem and NP-hard,it is challenging to obtain optimal solutions within polynomial complexity[30].

III.EE-SUBOPTIMAL POWER ALLOCATION ALGORITHM

In this section,we first establish the feasible range of power consumption ratio that can support the minimum QoS requirement for each SU.Then,we decouple the original problem into two optimization sub-problems:sub-carrier power allocation and subcarrier power consumption ratio,and describe each sub-problem respectively.And finally,the computational complexity of the proposed PA algorithm is analyzed.

3.1 The Feasible Range of Power Consumption Ratio

In this subsection,we solve the minimum power consumption ratio problem based on the Lagrange function and the Karush-Kuhn-Tucher (KKT) condition under the minimum QoS requirement for each SU and the effectiveness requirement of the SIC receiver.

The minimum power consumption ratio of subcarriermcan be expressed as

From Eq.(9),we have known that the optimization goal of the minimum power consumption ratio of the sub-carrier is an affine function,which can be regarded as a convex function.Because the corresponding constraint conditions are all linear,the sets composed ofC2andC4are convex.

Based on convex optimization theory [31],the Lagrange function of Eq.(9)can be expressed as follows

where,µ,ωandλare Lagrange multipliers.

Since problem (10) is convex,the following KKT conditions are necessary and sufficient for the optimality.Set the partial derivatives of(10)w.r.t.α,µ,ωandλto zero respectively,we may get

From Eq.(11),we know that all the inequationsλi >0,µi >0,ωi >0 are permanent for anyi ∈L.Therefore,the closed expression of the optimal solution for the minimum power consumption ratio of subcarriermis given by

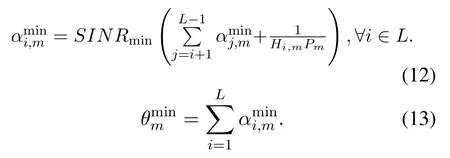
Combined Eq.(6) and Eq.(13),the feasible range of power consumption ratioθmisIn uplink underlaying CR-NOMA networks,the SUs move slowly or even be static especially for mMTC scenario,the feasible range of power consumption ratioθmmay be further narrowed according to the latest optimal values.

3.2 Energy Efficiency Optimization Problem Analysis

Because the total system EE optimization problem of(8)is a non-linear fractional programming problem,it is necessary to transform the original problem into an equivalent form.The total throughput of (7) can be rewritten as[23,32]

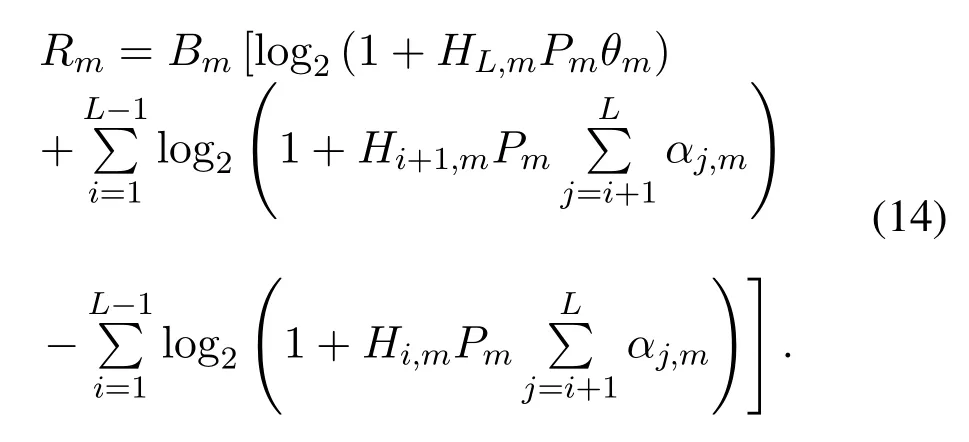
Based on Eq.(14),the total system EE formula(8)can be rewritten as

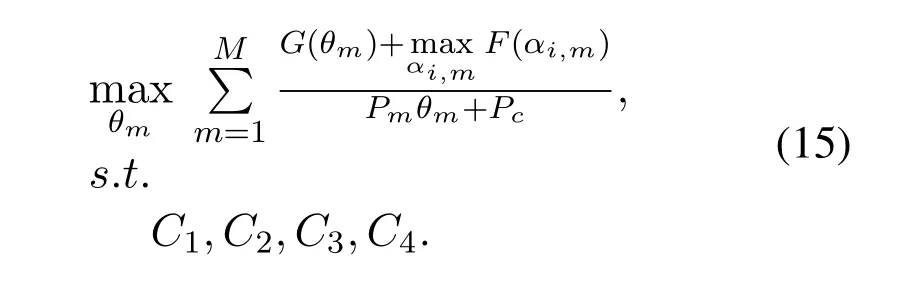
where,G(θm)andF(αi,m)are defined as follows

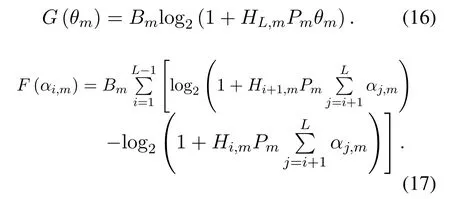
From Eq.(15),we know thatF(αi,m) is a function concerning the single variableαi,m,G(θm) andPmθm+Pcare functions respecting to the unique variableθm.Obviously,the DC and Dinkelbach algorithms are both classical methodologies for handling PA in NOMA system.The former algorithm is usually employed to approximate the addition or subtraction of polynomials,and the latter algorithm is usually employed to approximate the division of polynomials.For the EE maximization problem (15) composed of addition and division of polynomial,it is more suitable to use the DC algorithm and Dinkelbach algorithm together in essence.

To effectively solve the EE optimization PA problem of formula(8),the original optimization problem can be split into two sub-problems:sub-carrier power allocation sub-problem and power consumption ratio sub-problem.The inner-layer optimization problem is performed over argumentsF(αi,m) by takingθmas a constant value,the solution of which is a function ofθm.The outer-layer optimization problem is taken overθmto maximize the system EE.A sub-carrier PA strategy based on the DC algorithm is used to solve the inner-layer optimization problem and obtain the optimal PA coefficientsα∗i,m.Based on them,the optimalθ∗mwhich maximizes the EE may be found using the Dinkelbach algorithm in this subsection 3.4.These two sub-problems sequentially are solved to approximate the optimal solution of the EE problem.

Because the first givenθ∗min the feasible range of the inner optimization problem is not always optimal,so it may need several outer-layer and inner-layer iterations to get the convergent values.Although the original problem of Eq.(8) is a multi-variable optimal problem,we may employ the convergent values of the iterative DC and Dinkelbach algorithm with a single variable to approximate the optimal solution of Eq.(8).Only in this case,both the PA coefficientαi,mand the power consumption rateθmmay approximate their optimal values,the optimization problem(8)can be rewritten as(15).

3.3 Sub-carrier Power Allocation Algorithm

For a given∈M,the subcarrier PA sub-problem can be rewritten as follews

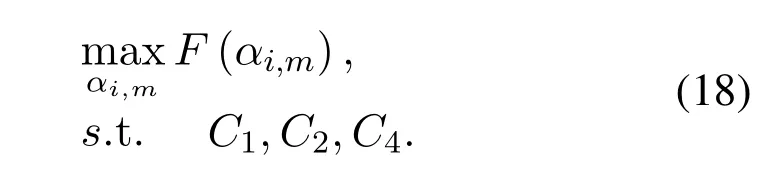
It can be seen that the objective function of(17)can be written as the difference of two functions using dual theory.The sub-carrier optimization PA problem(18)can be written by

where,

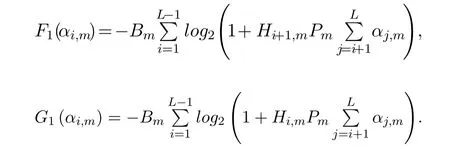
From the above subsection,we have known that the constraint conditionC4is convex,the constraint conditionsC1andC2are both linear,so the sets formed by them are also convex.

Because the first-order partial derivative ofF1(αi,m) toαi,mis less than zero and the secondorder partial derivative ofF1(αi,m) toαi,mis more than zero,that is,

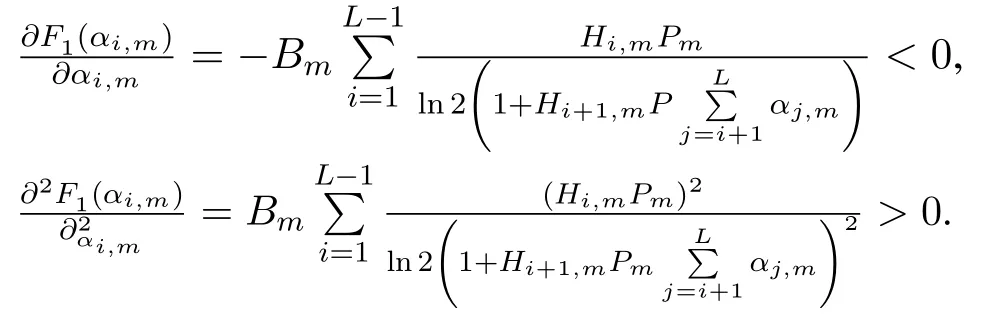
Therefore,F1(αi,m) is a convex function ofαi,m.similarly,we may get thatG1(αi,m) is also convex.Accordingly,the problem (19) can be solved by invoking the DC programming[33].

Although the problem (19) is still non-convex,the continuous convex approximation may be employed to transform it into a series of approximate convex problems to achieve an efficient suboptimal solution by adopting an iterative approach.Therefore,the functionG1(αi,m) can be approximated by its first-order Taylor expansionwhererepresents the first-order partial derivative ofαi,mat(·)Tdenotes the transpose operation.Under an additional assumption thatF1(αi,m) andG1(αi,m) are continuous and differentiable on the constraint set,Algorithm 1 always returns a stationary point of[34].

From the above description,we know that the subcarrier PA algorithm can be expressed by DC programming first,and then the minuend function may be approximated by its first-order Taylor expansion,an iterative solution of the original problem may be achieved.

The detailed solution process of the sub-carrier suboptimal PA problem based on DC programming is given in Algorithm 1.

3.4 Power Consumption Ratio Algorithm

Substituting the current optimal PA coefficientsα∗i,m(θm) obtained from the above subsection into(15),the power consumption ratio problem can be transformed into a univariate optimization problem w.r.t.θm,which is given by

?

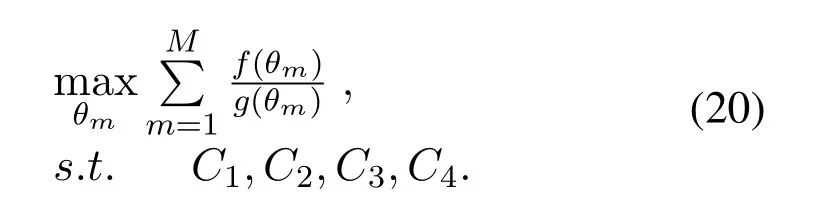
where,

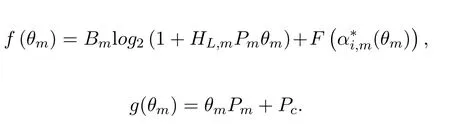
The optimal solution of problem(18)is denoted by

According to the convex optimization theory [35],the objective function of formula (20) is a concave convex fractional programming (CCFP) problem,where the numerator and the denominator of(20)are respectively concave and convex function,and the constraint set is convex.

Theorem 1.Problem(20)is a CCFP problem.

Proof 1.Because the first-order partial derivative of G(θm)in(16)to θm is more than zero and the secondorder partial derivative of G(θm)to θm is less thanzero,that is,

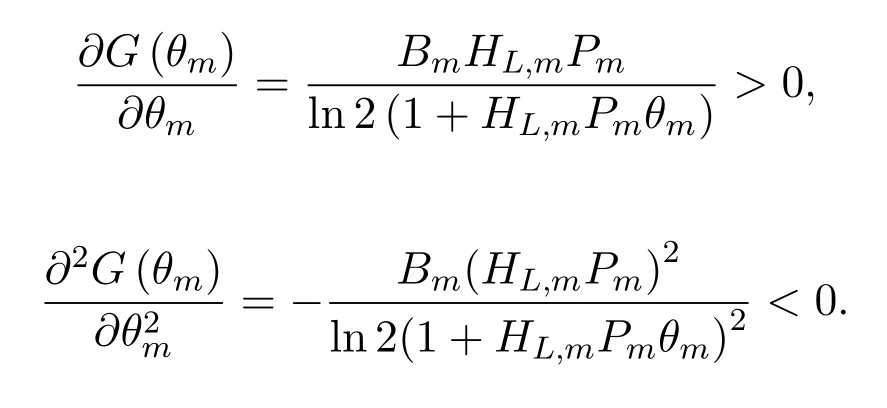
Therefore G(θm)is a concave function of θm.Fur-thermore,the function ofin (19) is con-vex [34],and we know from (18) that F(αi,m)=so the functionand f(θm)are all concave functions.Because the power consumption is always bigger than zero,g(θm)>0,and which is an affine function of θm with linearity constraint qualification,thus g(θm)is a convex function.Therefore,the numerator of (20) is a concave function concerning θm,and the denominator is a convex function concerning θm,too.The constraints of problem (20) can be written as linear two inequalities,so the feasible region formed by them is also a convex set.By now,we have proved that the problem(20) is a CCFP problem,where the numerator is a concave function,the denominator is a convex function,and the constraint is a convex set.

For the CCFP problem,the Lagrangian relaxation model can be converted from the objective function(20)into an easier sequence problem invoking Dinkelbach algorithm as follows.

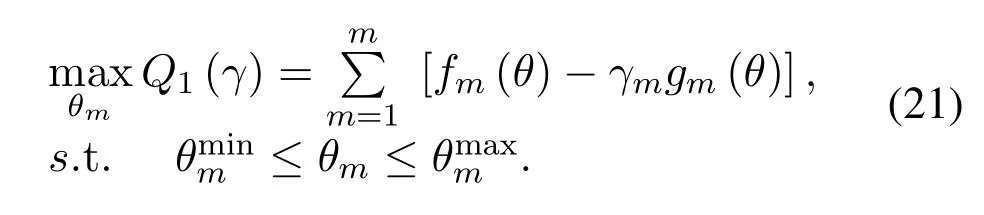
In Eq.(21),γ=[γ1,γ2,···,γL]is auxiliary variables for each SU on sub-carrierm,fm(θ)=G(θ)+gm(θ)=Pmθ+Pc.Whenγachieves the optimal value,the following equation is establishedFor any givenγ,fm(θ) is a concave function andγmgm(θ) is an affine function,so the objective function of(21)is a concave function.

Furthermore,the constraint condition of(21)is convex,so the problem of (21) can be approximated by using the Lagrange function,which can be expressed as

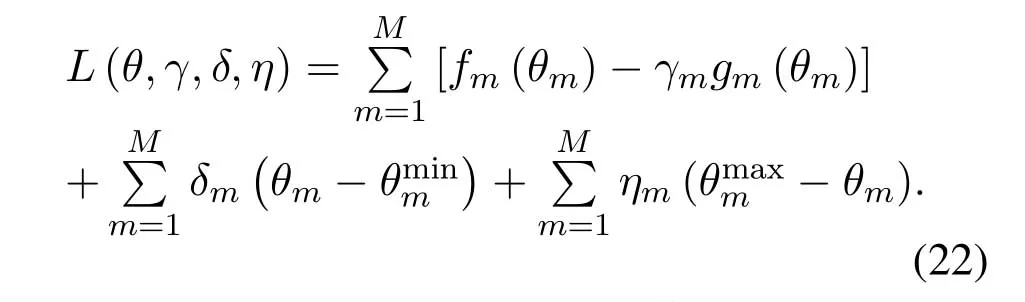
where,δandηare Lagrange multipliers.

Set the partial derivatives of (23) w.r.t.θm,γ,δandηto zero respectively,we may get the KKT conditions.Finally,the closed expression of the optimal power consumption rateθ∗mcan be obtained as follows

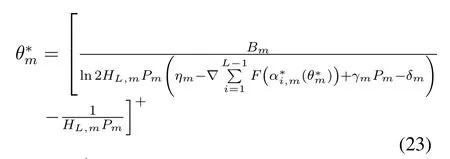
where[v]+=max(0,v).

The subgradient method is adopted to update the Lagrangian multipliersδandη,which can be expressed by

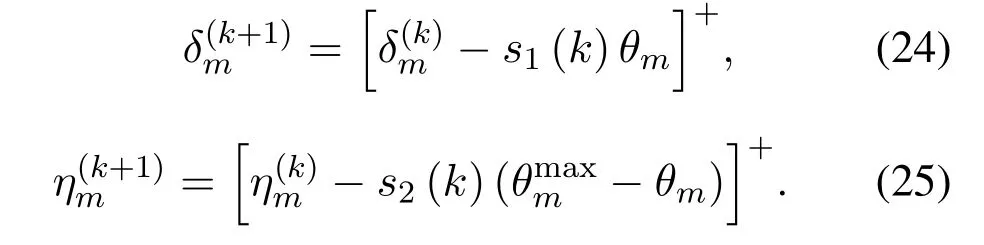
Algorithm 2 gives the process of the iterable subcarrier power consumption ratioθby using Dinkelbach programming.

3.5 Computational Complexity Analysis

In this subsection,we analyze the computational complexity of the proposed algorithm and the comparison algorithms.The FSPA algorithm needs to search for all the possible combinations of multi-users based on the maximum total throughput in [36].The overall computational complexity of the FSPA algorithm isO(2N),so it is hard to be applied for engineering,whereNis the multi-user number on a sub-carrier.SA is a stochastic computational method for finding global extremum to the optimization problem,which can be employed for PA in the NOMA system.The computational complexity of the SA algorithm is excessively high,which can be described byO(2NN4)[37,24],whereNis the multi-user number on a subcarrier.

?

Although the minimum power consumption ratio is derived based on the Lagrange function and the KKT condition in subsection 3.1 of this section,the minimum and maximum power consumption ratio may be also calculated by the fixed or estimated values before the EE-based power allocation process.Furthermore,the feasible range of power consumption ratio may be further narrowed according to the latest convergent values in uplink underlaying CR-NOMA networks for practical application.Therefore,the computational complexity of calculating the feasible range of power consumption ratio may be ignored.The whole computational complexity of the proposed PA algorithm can be divided into two parts:the DC algorithm and the Dinkelbach algorithm.Let us consider that it takes an average iterationT1to converge for the DC algorithm,all the computational complexity of above DC algorithm for the system consisting of numberNof the multi-user and numberMof sub-carriers isO(T1NM).The Dinkelbach algorithm progress contains three loops,which areM,NandLrespectively,so the computational complexity is approximated toO(T2NLM)with an average iterationT2.As can be seen from the above analysis,the computational complexity of FSPA algorithm and SA algorithm are both exponential increases with multiuser numberN,however,the computational complexity of the proposed algorithm is polynomial increase with multi-user numberN.

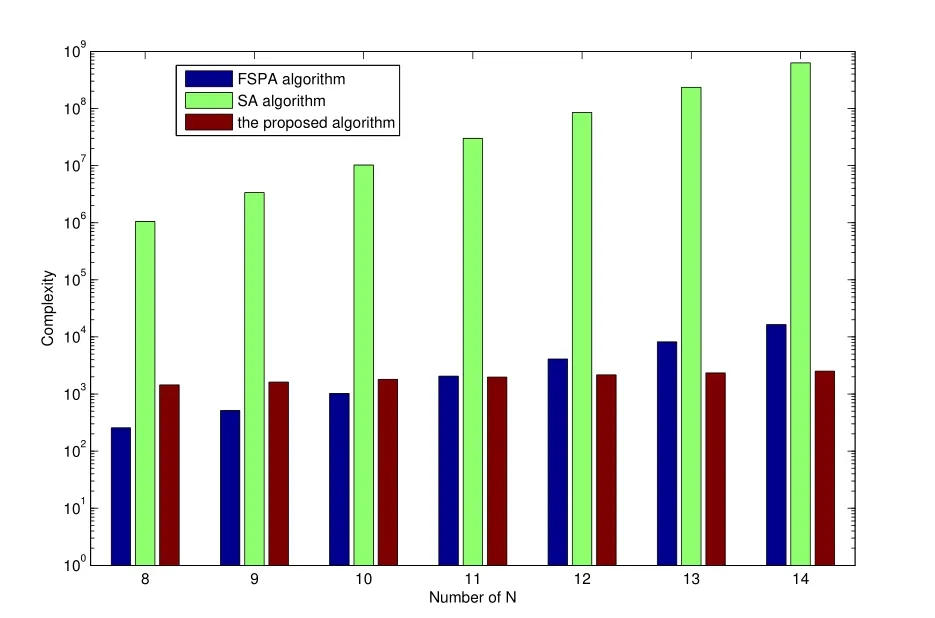
Figure2.Complexity comparison of different algorithms.

In Figure2,we compare the computational complexity between the proposed algorithm with FSPA algorithm and SA algorithm,whereL=3,M=5,

T1=5,T2=10,N=8,9,...,14.We can see that the computational complexity of SA algorithm is much greater than that of the other algorithms.When multi-user numberNis less than or equal to 11,the computational complexity of the proposed algorithm is higher than that of FSPA algorithm.However,the computational complexity difference between the proposed algorithm and the compared algorithm is very small.When multi-user numberNis more than 11,the computational complexity of the proposed algorithm is lower than that of the FSPA algorithm.Furthermore,both the average inner-layer and outer-layer iteration number can be reduced further when the feasible range of power consumption ratioθmmay be narrowed for the SUs of mMTC application.Even though,the computational complexity of the proposed algorithm is also at the acceptable level.In summary,the proposed algorithm is much lower than that of FSPA algorithm and SA algorithm,especially for bigger multi-user numberN.

IV.SIMULATION ANALYSIS

4.1 Simulation Paraments and Assumptions

In this section,the proposed energy-efficient power allocation algorithm performance is illustrated in uplink underlaying CR-NOMA networks,the fractional power allocation (FPA) algorithm [38]and SA algorithm[39]are adopted as comparison algorithms.

The following simulation parameters are summarized as follows:the SUs are uniformly distributed in a circular range with a radius of 500m,the minimum distance between each SU is set to 40m,the minimum distance between SUs and secondary BS is 50m,the receiver noise figureis 7dB[40],the bandwidth is 5MHz,sub-carrier spacing is 15KHz,the total noise power at the receiver is-75dBm,the circuit power consumptionpcis 20 dBm[34],the number of PUs in the cellular is 5,the maximum interference power from PUmis-30dBm,and the toleranceεis 0.01[41,42].

4.2 Simulation Results

To investigate the performance of the proposed PA algorithm for the secondary SUs based on the ASEE through extensive Monte Carlo simulation,more than 104samples per simulation are acquired to ensure sufficient statistical confidence.In the following,we investigate six aspects of the performance of the proposed algorithm.The relationship between ASEE/total system throughput and the number of inner-layer and outer-layer iteration,the minimum SINR,the total transmit powerPtot,the interference power limitationIm,the number of SUsN,and circuit power consumptionpcare demonstrated in Figure3-Figure10,respectively.

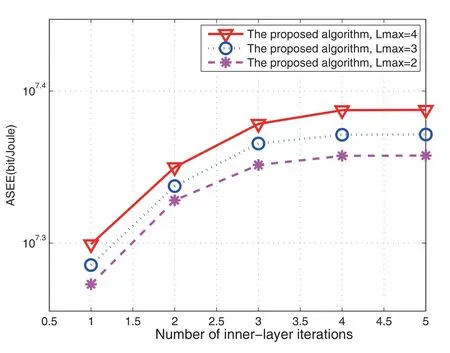
Figure3.Relationship between ASEE and number of innerlayer iterations.

Figure3 illustrates the convergence tendency of the proposed algorithm using the DC algorithm when the maximum multiple SUs numberLmaxare 2,3,4,respectively,the total transmit power allocatedPtotis 35dBm,the number of exterior iterations is about 10.From Figure3,we can know that for a given power consumption ratioθm,the sub-carrier power allocation algorithm of DC may get the convergence values when the number of inner-layer iteration is bigger than 4.We can also get that the ASEE increases with the maximum multiple SUs number,because the total system throughput may get more.Therefore,the sub-carrier power allocation algorithm has good convergence performance for the current radio channel environment.

Figure4 illustrates the convergence tendency of the proposed algorithm compared with SA algorithm when the multiple SUs numberNis 3,and the total transmit powerPtotallocated are 25dBm and 35dBm.As can be observed that the ASEE of both algorithms increases and converges to the fixed values as the increase of outer-layer iteration when the number of inner-layer iteration is 5.At the same time,the ASEE of the proposed algorithm whenPtot=35 dBm is better than that ofPtot=25 dBm about 1.5×107bits/Joule for the iteration number is about 100.Although the final ASEE of the proposed algorithm is slightly less than the SA algorithm about 2% for the iteration number is about 100,the proposed algorithm can achieve its optimal ASEE when the iteration number is about 10,but SA algorithm achieves its optimal ASEE when the iteration number is about 60.Therefore,the proposed algorithm possesses faster convergent speed than SA algorithm.

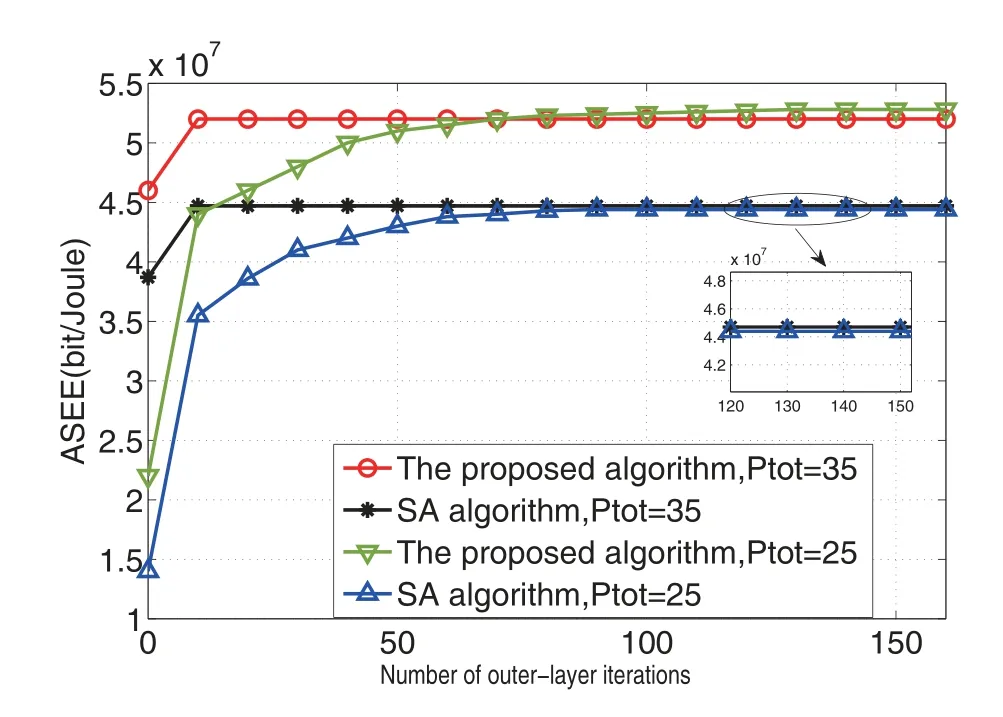
Figure4.Relationship between ASEE and number of outerlayer iterations.

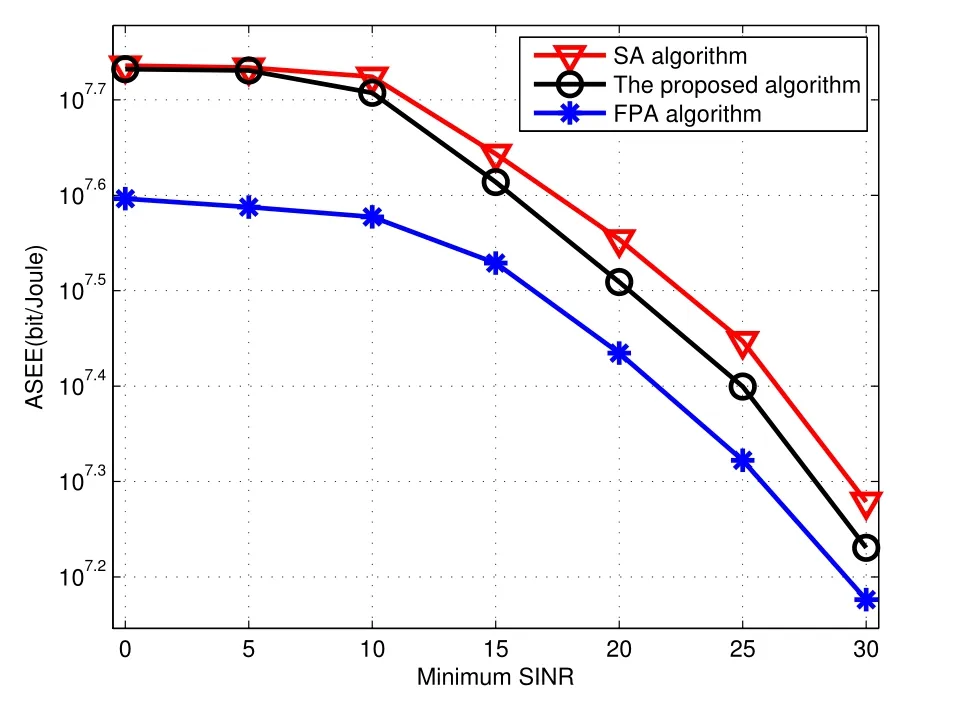
Figure5.Relationship between ASEE and minimum SINR.

Figure5 illustrates the relationship between ASEE and the minimum SINR from PU when the multiple SUs numberNis 3.The ASEE of the proposed algorithm,SA algorithm and FPA algorithm decreases together with the increase of minimum SINR,because less power may be allocated for SUs.SA algorithm can achieve the global optimal EE,and FPA algorithm only considers the total throughput performance,so the ASEE of the proposed algorithm is slightly lower than SA algorithm about 0.1×107bits/Joule,but which is much better than FPA algorithm about 1.5×107,when the minimum SINR is about 10dB.The relationship between the total system throughput and the total power available of SUs is given for SA algorithm,the proposed algorithm and FPA algorithm in Figure6.The total system throughput of the proposed algorithm is slightly lower than SA algorithm,because SA algorithm may get the global optimum,the proposed algorithm only get the suboptimal solution because of the performance loss during the DC and Dinkelbach algorithm approximation process.However,both of them may be better remarkably than FPA algorithm for its algorithm strategy is not precise enough.

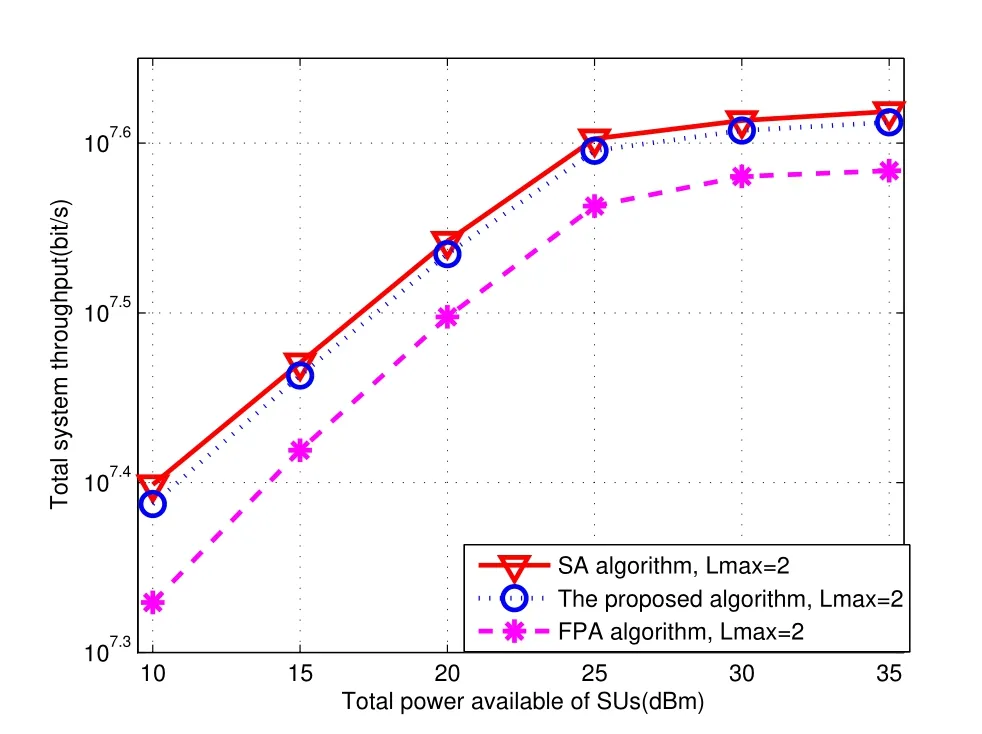
Figure6.Total system throughput vs.the total power available of SUs.

Figure7 illustrates that ASEE versus the total power of primary BSPtotwhen the number of SUs is 2 and 3,SINRmin=3dB.According to the increase ofPtot,the maximum ASEE of the proposed algorithm may be slightly smaller than SA algorithm.The maximum ASEE of the proposed algorithm whenLmax=3 is better than that ofLmax=2 about 0.25×107bits/Joule when the total power of primary BS is 35dBm.The optimal ASEE of SA algorithm may get a similar performance,because the actual transmission power demand of SUs will no longer increase with the increasing ofPtotwhen the above two algorithms reach their maximum EE restrictive conditions.However,for FPA algorithm,the ASEE increases with the increasing ofPtotfirst,and then declines whenPtotis bigger than 30dBm.Because FPA algorithm always requires more transmit power allocated for the weaker channel gains of SUs to achieve the maximum total throughput,but the FPA algorithm can not get the corresponding total throughput improvement whenPtotis larger than 30dBm.

Moreover,NOMA is superior to OMA in terms of EE,and the performance gains of NOMA become more significant as K increases because when more users are simultaneously served,higher diversity gains and higher SE can be achieved.

Figure8 depicts the relationship between ASEE and the maximum tolerable powerImfrom PUm.The ASEE increases with the increasing ofImand converges to the maximum values for all the three algorithms.At the same time,the ASEE of the proposed algorithm when the number of SUs is 3 is better than that of the number of SUs is 2 about 0.2×107bits/Joule forIm=−40 dBm.When the maximum tolerable powerImfrom PUmincreasing,the available power for SUs is also gradually increasing until the available power reaches the maximum value.At last,the ASEE performance of the proposed algorithm is slightly lower than SA algorithm,but is much better than FPA algorithm.

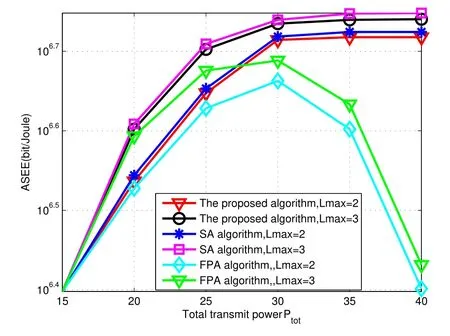
Figure7.Relationship between ASEE and the total power available of SUs.

Figure8.Relationship between the ASEE and the maximum interference power from PU m.

Figure9 shows the relationship between ASEE and the numberNof SUs in uplink underlaying CRNOMA networks.The ASEE of three algorithms increases and converges to the fixed values as the increase of SUs,because the number of multiple SUs may reach the maximum allowed value.At the same time,the ASEE of the proposed algorithm when the number of SUs is 3 is better than that of the number of SUs is 2 about 0.3×107bits/Joule for the number of SUs is about 40.The ASEE of the proposed algorithm is slightly lower than SA algorithm,but is much better than that of FPA algorithm when it converges to the fixed values.

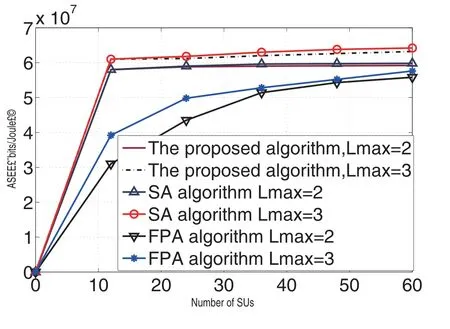
Figure9.Relationship between ASEE and the number of SUs.

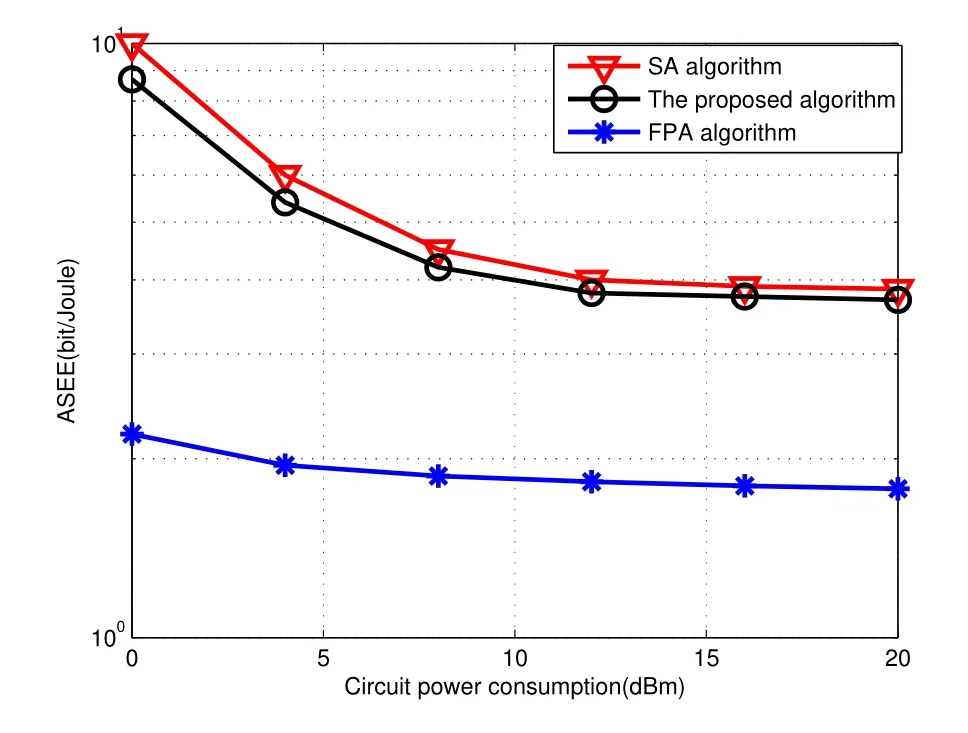
Figure10.Effect of circuit power consumption pc.

As can be seen in Figure10,the ASEE performance and the corresponding circuit power consumption are demonstrated for different power allocation algorithms.The ASEE decreases with an increase in circuit power consumption at the receiver end,and the tradeoff characteristic depends on the wireless link power gain between each UE and the receiver.More specifically,when UEs have relatively favorable channel conditions,i.e.,higher gains,each incremental circuit power hurts the EE significantly.

From the above analysis,we know that the proposed algorithm possesses good convergence performance,and the EE performance which is slightly lower than SA algorithm is much better than FPA algorithm.

V.CONCLUSION

In this paper,we have studied the EE-based PA algorithm for IoT devices in uplink underlaying CRNOMA networks.Firstly,a suboptimal EE algorithm is formulated to achieve the green design goal of SUs as IoT devices under the interference constraints from PUs.The feasible range of power consumption ratio is formulated based on the KKT conditions according to the minimum QoS requirement of each SU.Then,the original problem can be decomposed into two subproblems:sub-carrier power allocation and power consumption ratio.In the inner-layer sub-problem,the DC programming is employed to approximate the nonconvex PA problems based on Duality Theory and the first-order Taylor expansion.Based on the solution of the inner-layer sub-problem,the optimal power consumption ratio can be solved for the outer-layer optimization sub-problem by applying the fractional programming Dinkelbach algorithm and the Lagrangian multipliers which are updated using the sub-gradient method.Finally,the computational complexity of the proposed algorithms is analyzed,and compared with SA algorithm and FSPA algorithm.Simulation results show that the ASEE performance of the proposed algorithm with faster convergent speed and lower computational complexity is slightly less than that of SA algorithm,but which is much better than that of FPA algorithm.

ACKNOWLEDGEMENT

This work is supported in part by the Science and Technology Research Program of the National Science Foundation of China (No.61671096),Chongqing Research Program of Basic Science and Frontier Technology (No.cstc2017jcyjBX0005),Chongqing Municipal Education Commission (No.KJQN201800642)and Doctoral Student Training Program(No.BYJS2016009).