Shortest Link Scheduling in Wireless Networks with Oblivious Power Control
Chunmei Ma,Jiguo Yu,Baogui Huang,*,Yu Meng
1 School of Computer Science,Qufu Normal University,Rizhao 276826,China.
2 School of Computer Science and Technology,Qilu University of Technology(Shandong Academy of Sciences),Jinan 250353,China.
3 Shandong Computer Science Center(National Supercomputer Center in Jinan),Jinan 250014,China.
4 Shandong Provincial Key Laboratory of Computer Networks,Jinan 250014,China.
5 School of Computer Science&Technology,Georgia State University,GA 30303,USA.
Abstract:Link scheduling has always been a fundamental problem in wireless networks for its direct impacts on the performance of wireless networks such as throughput capacity,transmission delay,lifetime,etc.Existing work is mainly established under graphbased models,which are not only impractical but also incorrect due to the essentially fading characteristics of signals.In this paper,we study the shortest link scheduling problem under two more realistic models,namely the signal to interference plus noise ratio(SINR)model and the Rayleigh fading model.We propose a centralized square-based scheduling algorithm(CSSA)with oblivious power control under the SINR model and prove its correctness under both the SINR model and the Rayleigh fading model.Furthermore,we extend CSSA and propose a distributed square-based scheduling algorithm(DSSA).Note that DSSA adopts CSMA/CA so that a wireless node can compete for the wireless channel before starting its communication.We also show theoretical analysis and conduct extensive simulations to exhibit the correctness and efficiency of our algorithms.
Keywords:link scheduling;SINR;Rayleigh fading;wireless networks;wireless communications
I.INTRODUCTION
As one of the fundamental problems of wireless networks,link scheduling plays an important role in improving network performance,such as achieving high network throughput and fairness,extending network life,reducing average waiting time of the sensor nodes,increasing channel utilization and the probability of successful transmission.In theory,link scheduling problems are closely related to fundamental issues in wireless networks,such as coverage,connectivity,capacity,delay,etc.The goal of the link scheduling problem is to improve the quality of service(QoS)or quality of experience(QoE)[1].In addition,the interference caused by simultaneous link transmissions is very complicated.Therefore,it is extremely difficult to design an efficient link scheduling algorithm.
On the one hand,the key to solving link scheduling problems is to study the interference among the simultaneous wireless transmissions.On the other hand,the interference model has great impact on the complexity of the optimal wireless link scheduling algorithm.Therefore,how to choose an appropriate interference model has become a crucial step in wireless link scheduling.Existing work(such as[2–4])has extensively studied link scheduling problems under the graph model.However,there is a huge difference between the actual network environment and the graph model.That is,the interference constraints of simultaneous transmissions are neither local nor in pairs,but global and accumulative,which leads to a large amount of emerging research under the signal to interference plus noise ratio(SINR)interference model[5–10].The SINR model better reflects the interference in the actual network than the graph model.Unfortunately,Goussevskaiaet al.[8]proved that link scheduling problem under SINR is NP-hard.
For signal propagation,some research adopts the path loss exponential model,in which any signal transmitted with power levelPtis always received beyond distancedwith strengthPtd−α,where 2<α <6 is the path loss exponent.In fact,the signal propagation is by no means deterministic in reality due to multipath fading [11].Rayleigh distribution is often used to model the multipath fading without direct line-ofsight (LOS) path [12].Although the Rayleigh fading model is closer to link transmission characteristics in real world scenarios than the path loss exponential model,it is more difficult to design the optimal wireless scheduling algorithm under the Rayleigh fading model,because the received power of the receiver is a random variable rather than a determinate value.Recently,many link scheduling algorithms under the Rayleigh fading model have been proposed,such as[13].
For wireless networks,such as wireless sensor networks,saving energy to extend the life of the networks is an important issue [14,15].Therefore,when designing link scheduling algorithms for wireless networks,another issue we need to consider is the power assignment,since power assignment is a critical technique to improve throughput and save energy[16,17].Existing power control schemes can be roughly classified into the following two types:fixed power control and arbitrary power control.For the fixed power control,power is part of the input,and in case of the arbitrary power control,choosing the appropriate power to optimize the capacity is part of the problem.For ease of implementation in distributed settings,research on both fixed and arbitrary power control has focused on oblivious power assignment [7,18–20],which is the power assignment we choose for the proposed model.
The main contributions are as follows.
(1) We propose a centralized square-based link scheduling algorithm (CSSA) under the SINR model and oblivious power control.Obviously,for a large wireless network distributed link scheduling algorithms are more competitive than centralized algorithms.Because centralized algorithms require global information of network area,nodes position and the length of links,etc.However,it is difficult to obtain this information.While distributed algorithms only need local information,which is easy to obtain.Therefore,we extend CSSA and propose a distributed algorithm similar to CSSA,called distributed square-based schedule algorithm(DSSA).
(2) DSSA adopts CSMA/CA technology to avoid conflicts.Before sending a message,the sender first competes for the wireless channel and sends the message with probability.If the sender transmits a message,it informs its neighbors that the channel will be occupied.In this way,its neighbors cannot send messages at the same time.
(3) We prove the correctness of CSSA under the signal to interference ratio (SIR) model that neglects the ambient noise.In addition,as long as the transmission power is increased appropriately,the CSSA proves correct under theexactSINR model.In this regard,the oblivious power control plays an important role since the“appropriate”transmission power can be easily set under the oblivious power control.
(4) This paper combines the SINR model with the Rayleigh fading model.Because the power of the received signal is a random variable,the received signal is decoded correctly with probability under the Rayleigh fading model.We prove that the probability of successful transmission of each link in a slot under the Rayleigh fading model,saySt,is no less thanthen according to Corollary 4 of [11],Stis a feasible set under the SINR model.Therefore,CSSA and DSSA are also effective under the Rayleigh fading model.
The rest of this paper is organized as follows.In Section II,we review related work.Then,we give a detailed description of the network topology,channel model and power control.In Section IV,we propose the CSSA algorithm and analyze the correctness and performance under the SINR model and the Rayleigh fading model.We extend CSSA and propose a distributed algorithm called DSSA in Section V.In Section VI,considering the ambient noise,if the transmission power is increased appropriately,we prove that CSSA and DSSA are correct.In Section VII,we compare our algorithms with existing algorithms through theoretical analysis and simulations.Finally,we summarize the paper and discuss further work in Section VIII.
II.RELATED WORK
In[5],Moscibroda and Wattenhofer studied the wireless link scheduling problem based on the SINR model and proved that the scheduling complexity of the connected set was logarithmic polynomial growth with the number of nodes.In addition,they put forward a scheduling algorithm that could successfully schedule the strongly connected set with time complexity ofO(log4n) in any networks,wherenis the number of nodes.In [21],Moscibrodaet al.further studied the scheduling complexity problem in wireless networks with any topology and proposed a scheduling algorithm with time complexity ofO(Iinlog2n),withIinbeing a predefined static interference assessment.For the strongly connected set,ifIin ∈O(logn),the time complexity isO(log3n).
In[8],Goussevskaiaet al.proved that the wireless link scheduling problem under the geometry SINR model is NP-hard and proposed approximation algorithms for the shortest link scheduling problem and one slot scheduling problem.If the maximum and minimum link length is given,both algorithms obtain a constant approximate factor.However,the SINR model considered in [8]ignored background noise.Therefore,it was only an approximate SINR model.In [22],Chafekaret al.studied the throughput optimization problem under the SINR model and proposed a polynomial time complexity scheduling algorithm.Compared with the maximum available capacity under the uniform power assignment,the approximation factor of the algorithm isO(log ∆log Γ),where ∆is the ratio of the maximum and minimum link length and Γ is the ratio of the maximum and minimum power.In[20],Bloughet al.defined ablack-graylink whose SINR value lies in the range of [β,(1+σ)β),whereβ ≥1 and≤σ <1,and pointed out thatblack-graylinks affect the approximate bound of the shortest link scheduling problem.For the first time,a shortest link scheduling algorithm with deterministic boundary under theexactSINR model was proposed.However,they adopted the uniform power assignment,and assumed that all links could be 100%successfully scheduled,which largely limited the number of communication links scheduled simultaneously.Therefore,there is still room for improving the approximate limit.In[7],Halld´orsson considered the link scheduling problem combing power control with link diversity under the SINR model,and proposed anO(lognlog log ∆)-approximation factor algorithm,wherenis the number of links.In [18],Halld´orsson and Mitra further improved the approximate factor of unidirectional link scheduling toO(logn+log log ∆),which nearly matches the lower bound of Ω(log log ∆) for oblivious power assignment [7].In [23],Asgeirssonet al.proposed a completely distributed algorithm.Nodes do not require information about the entire network topology or even local information.They achieved an efficient ratio that was independent of the network size(i.e.,the number of links).Therefore,the algorithm is scalable in terms of network size.In [24],Peietal.presented the first low-complexity distributed link scheduling algorithm under the SINR model.They ensured a throughput region ofwhere ΛOPTrefers to the maximum throughput region under any scheduling and power control scheme,andg(L)is the link diversity.In[25],Wanet al.achieved 4βpapproximation ratio for maximizing the wireless network capacity with linear transmission power assignment under the SINR model,whereβpis less than 20 in the bidirectional mode and less than1) in the unidirectional mode,wherec>1.In[26],Xuet al.proposed stable link scheduling protocols in wireless networks under the SINR model with the uniform power setting and monotone power setting.The protocols achieveO(1/logn)-fraction of the capacity region.
It is wise and efficient to design distributed algorithm for a large scale wireless network [27–30].In[30],Zhouet al.studied localized scheduling for capacity maximization under the SINR model with the oblivious and the uniform power assignment.The algorithm achieves a constant andO(logn) fraction of capacity region for the oblivious and uniform power settings,respectively,wherenis the number of nodes.In[31],Yuet al.proposed a series of algorithms based on plane partition.They partitioned the network area into hexagons and colored them in 3 colors.In a time slot,they selected no more than one link of the same color from each hexagon for scheduling.
The major drawback of the SINR model is that if the transmission power is fixed,the received power of the receiver is determined,which ignores the impact of multipath fading on signal transmission.In [11,32],Damset al.studied the wireless scheduling problem under the Rayleigh fading model.They pointed out that one could apply existing algorithms for the nonfading model (such as SINR) in the Rayleigh-fading scenario while losing only a factor ofO(log∗n)in the approximation guarantee.Where,
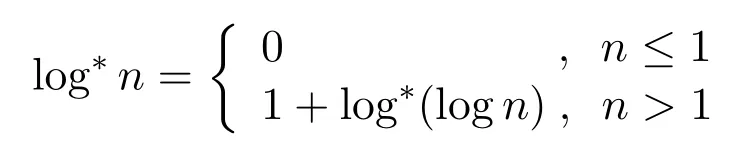
They discovered the following important relations between the probability of successful transmission in the Rayleigh fading channel and the one in the non-fading channel.
LetLdenote the set of links.li=(si,vi)∈Ldenotes a link withsibeing the sender andvithe receiver.qidenotes the transmission probability ofsi.If a subsetS ⊆Lis feasible in the non-fading channel model,settingqi=1 for allli ∈Sandqi=0 for allli /∈S,then the success probability for each linkli ∈Sis at least 1/e.On the other hand,if the Rayleigh success probability is at least 1/for each link inS,andqi=1 for all links inS,thenSis feasible in the non-fading channel model.
This provides a theoretical foundation for us to study the link scheduling problem under the Rayleigh fading model in a similar way under non-fading model.This theory motivates us to design an effective shortest link scheduling algorithm that is effective under the SINR model and is also effective under the Rayleigh fading model.
III.NETWORK MODEL
3.1 The Network Topology
Given a setL={l1,l2,···,ln}of communication links,each linkli=(si,ri),i=1,2,...,nis the pair of communication nodes,i.e.the sendersiand receiverri.All nodes are deployed in a network regionF.The length ofliis defined as the Euclidean distance betweensiandri,denoted asd(li)=d(si,ri).The distance betweenliandljis denoted asd(lilj)=d(si,rj).The minimum length between two nodes is normalized to 1.sisends messages toriwith powerPsi.
The centralized link scheduling algorithm is executed by the central controller or SINK node,which collects the network information and links information and informs all senders scheduling results.In the rest of this paper,assume the central controller or SINK knows the network topology.For the distributed link scheduling algorithm,nodes have the following properties.
(1) Nodes are uniformly deployed in the network region,and they know their location information through GPS or other means.
(2) The network region is marked by a central position,which is consistent with the practical wireless network,such as a wireless network with a base station or an access point.The central position is shared by nodes.
(3)Each sender knows the potential receiver.In this case,the sender is aware of the communication distance.
(4)All nodes satisfy time synchronization.Time is divided into multiple time slots,and a message can be transmitted from the sender to the corresponding receiver within a time slot.
3.2 The Channel Model
3.2.1 SINR model The SINR model is more realistic and accurate than the graph-based interference model.Under the SINR model,when the senderstransmits a message with powerPsto the receiverr,the received power ofrisPsd−α(s,r),whereαis the path loss exponent,which is a constant between 2 and 6,and its value depends on the wireless environment.The received message can be successfully decoded if and only if the SINR value is no less than a specific thresholdβ.The SINR model can be formally defined as follows:the transmission over a linkl=(s,r) succeeds if and only if the following condition holds:
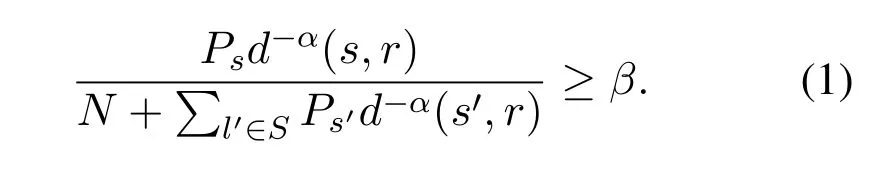
WhereNis the ambient noise,Sis the set of concurrently scheduled links.If each link inSsatisfies equation(1),Sis called a SINR-feasible set.
3.2.2 Rayleigh fading model
Under the Rayleigh fading model the instantaneous envelope of the received signal follows Rayleigh distribution.For a linkl=(s,r),the received power ofris a random variable of an exponential distribution with meanPsd−α(s,r),and the probability density function (PDF) of the received power ofr,denoted asis,
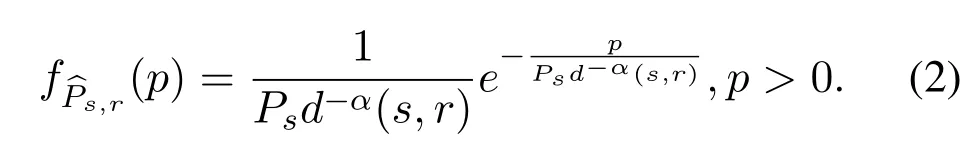
The interference power ofrcaused byl'=(s',r')scheduled simultaneously withlis denoted asThe probability density function ofis,
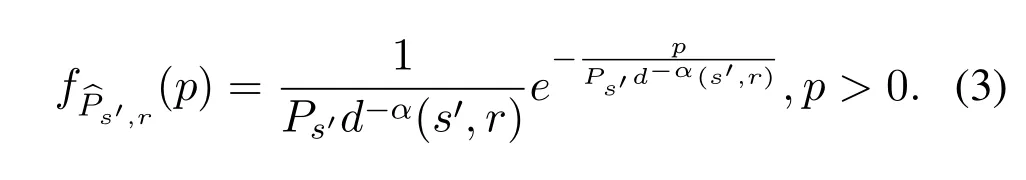
Assume thatI=x,under the SINR model,the probability thatl=(s,r) can successfully transmit signals is
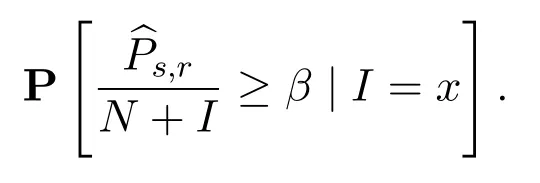
Assume the sendersi(i=1,2,...,n) transmits a message with probabilityqi,the probability ofrisuccessfully receiving the message isQi.Then,the relation between the success probability under the Rayleigh fading model and the success probability under the SINR model is as follows.
Lemma 1.(Corollary 4 in[11]) Assume the set S ⊆L is a SINR feasible set,SS is the set of senders of the links in S and RS is the set of receivers of the links in S.Let qi=1for all si ∈SS and qi=0for all si /∈SS,then Qi ≥1/e for all ri ∈RS.
If qi ∈{0,1} for all the senders and the Rayleighsuccess probability of each link is at leasttheset of links with qi=1is SINR feasible.
3.3 Power Control
For reasons of simplicity,many link scheduling algorithms consider the oblivious power assignment because the power mainly depends on the length of a given link.Two typical oblivious power assignment methods are uniform(or fixed)power assignment and linear power assignment.
Definition 1:Oblivious Power assignmentIf the power is determined by a simple function of the distance between the sender and receiver,it is referred to oblivious power assignment.
For a linkl=(s,r),the transmission power of the sendersisPs=ϕdα(s,r),whereϕ >βNis a constant related to a specific system environment.
3.4 Problem Definition
Given a setL={l1,l2,···,ln}of links,the shortest link scheduling problem is to find a scheduleS=(S1,S2,...,ST)satisfying the following:
(1)=L;
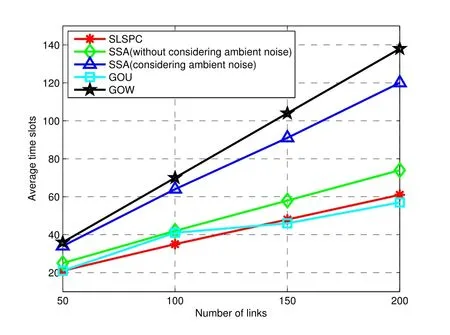
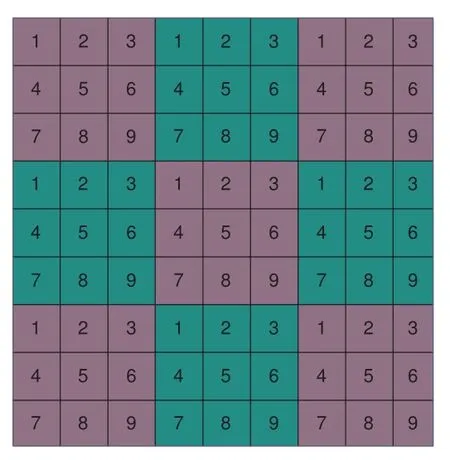
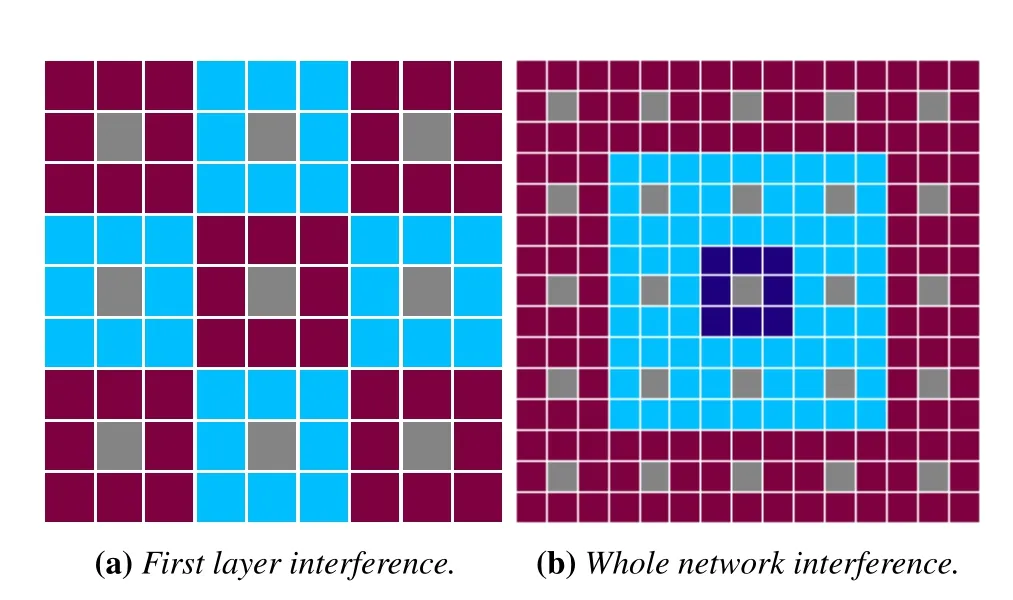
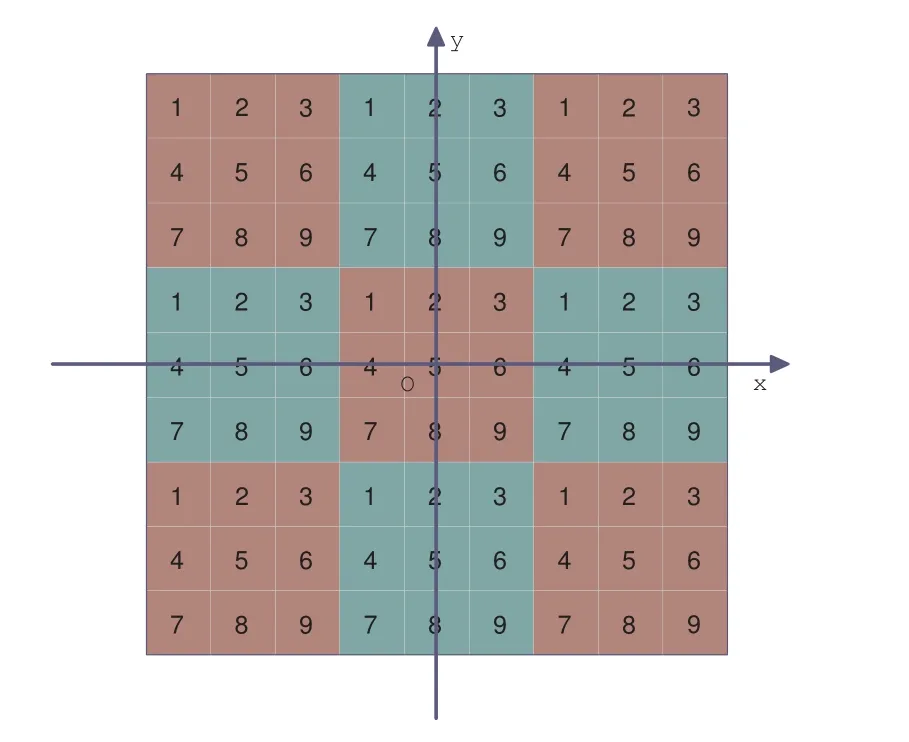
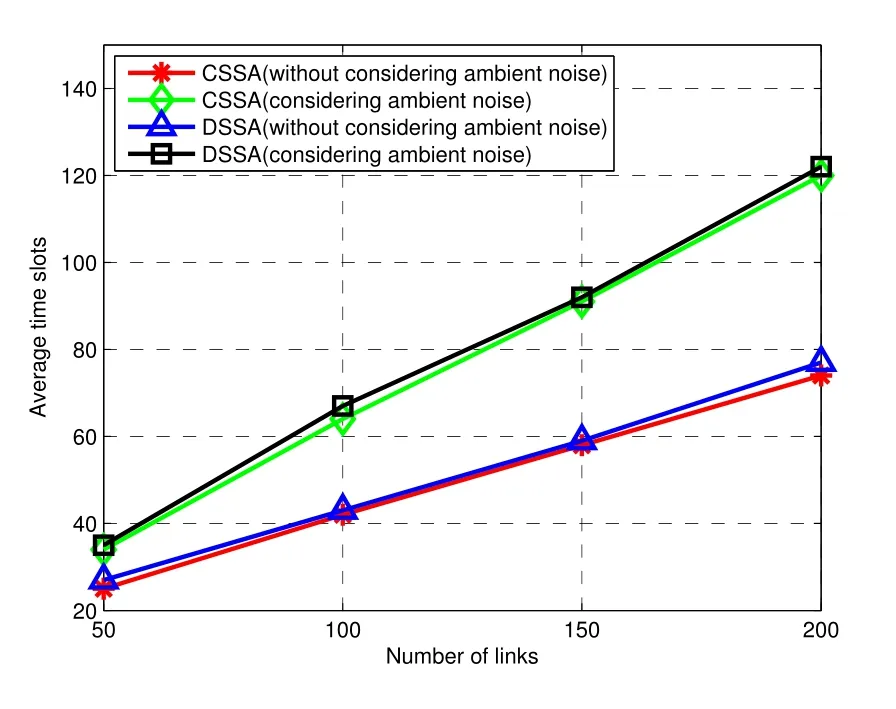
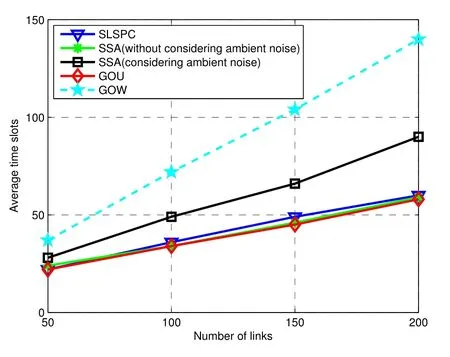
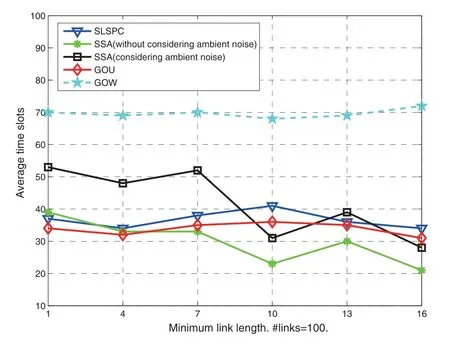
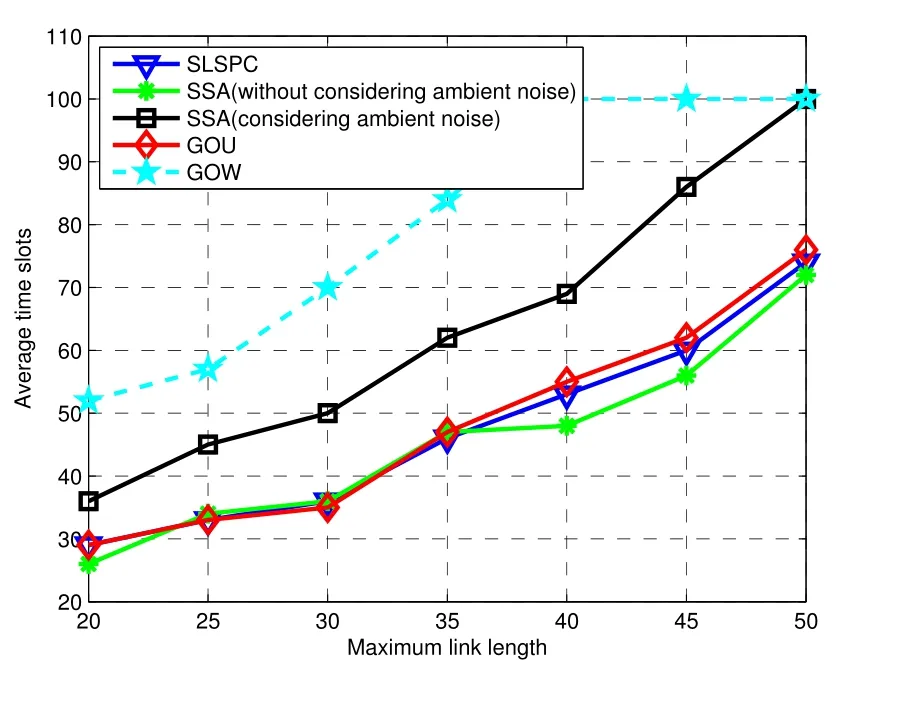
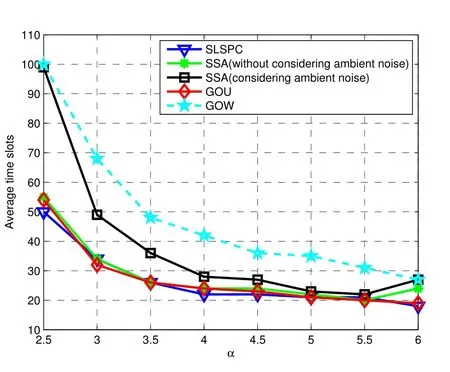
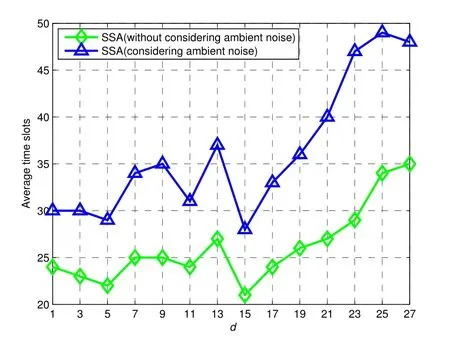
(2)for 1≤i (3) for 1≤t≤T,Stis a SINR-feasible set designated to time slott.That is,for each linkl=(s,r)∈St,the SINR inequality is satisfied atrwhen all senders inStare transmitting; (4)for each linkl=(s,r)∈St,1≤t≤T,the probability ofrsuccessfully receiving message is at least 1/ewhen all senders inStare transmitting under the Rayleigh fading model;and having the minimum possibleT. Given a set of linksL,letminlenandmaxlendenote the length of the shortest link and the longest link,respectively.In this paper,we divide the links into groups according to their lengths.Different from the algorithms proposed in[8],[20]and[33],we partitionLinto groups so that the number of links in each group is approximately equal. LetL=L1∪L2∪···∪LM,whereMis calledlink diversity.For∀l=(s,r)∈Lm,the length oflsatisfiesxm≤d(l) The big challenge in designing link scheduling algorithms is how to avoid interference.We found that interference is inversely related to distance.It means that the greater the distance between two links,the smaller interference the two links suffer.This conclusion motivates us to partition the network regionFinto small regions so that each link resides in a small region.Then we “arrange” the links which are far away from each other to transmit concurrently.Two problems should be considered when partitioning the network region.Problem 1 is how to ensure that the number of links in each small region is approximately equal so that scheduling holes can be avoided as much as possible.Recall that,all nodes are uniformly deployed in the network region.In this case,the number of links in each small region is approximately equal.Problem 2 is how to ensure there is no coverage hole,which means that the entire network region is partitioned into small regions while there is no overlapping small region.In order to solve the second problem,we partition the network region into regular small squares.Next,we propose a centralized square-based schedule algorithm(CSSA)under imprecise SINR model based on network region partition. We scheduleL1,L2,...,LMiteratively.For the subsetLm(m=1,2,...,M),we partition the network region into big squares with side lengthD=3a.Furthermore,each big square is partitioned into 9 small squares with side lengtha=µxm.Where,µis a constant and will be determined later.The 9 small squares are numbered 1,2,...,9 from top to bottom and left to right.As shown in figure1,small squares with the same number are separated by two small squares. Figure1.Network region partition. Next,we consider small squares marked with the same number (e.g.1).We randomly choose an unscheduled link from the links residing in the small squares numbered 1 for scheduling.The pseudo-code is listed in algorithm 1. ? Lemma 2.Assume li=(si,ri)∈Lm and li ∈St.The total interference of ri suffered from other nodesis bounded by Proof.Without loss of generality,assume thatliresides in a small square,sayA,which is numbered 5.That is,liresides in the center of a big square,as shown in figures 2a and 2b.The nearest 8 small squares numbered 5 are aroundA.The distance betweenliand the link in each of the 8 small squares is at least 2a −xm.We call the 8 small squares the first layer squares.Then,we consider the second layer,third layer,and so on.Next,we consider thehth layer squares.There are at most 8hlinks scheduled simultaneously,and the distance between each of them andliis at least(3h −1)a −xm.Therefore,the interferencerisuffered is Figure2.Interference of the link residing in the center of a big square. Theorem 1.Let µAssume N=0,under the SINR model each subset returned by CSSA is a SINR-feasible set. Proof.Without loss of generality,we examineStmentioned in Lemma 2.For∀li=(si,ri)∈St,the SINR value of receiverriis lower bounded by That is,Stis a SINR-feasible set. Here,the assumption ofN=0 is reasonable.1)In general,Nis very small and can be ignored in theoretical calculation.In fact,ifNis not equal to 0,as long as we improve the sender’s power,CSSA is correct(see section VI).2) In order to have the interference bound,we assume the network region is infinite.In fact,the network region is finite in the real network.Therefore,if we consider a finite region,the interference bound is smaller than that of lemma 2.3)Just as shown in figure1,when the ambient noise is ignored,the side length of a small square slightly decreases,which has a slight impact on the result.4) Lemma 2 is under the assumption that CSSA always selects one link from a square.If not,the interference decreases correspondingly.To sum up,the assumption ofN=0 does not impact the correctness of CSSA. Theorem 2.The approximation ratio of CSSA is O(M),whereis calledlink diversity. Proof.We examine the maximum number of links scheduled by the optimal algorithm OPT in a square.ForLm,the side length of the small square isa.Therefore,the maximum distance between two simultaneous transmissions is+xm.Letc0denote the maximum number of links scheduled by OPT.The SINR value of receiverriis That is, Obviously,c0is a constant sinceµis a constant.That is, In this paper,parameterdis important because it impacts the approximation ratio and the scheduling results.For example,ifd=c(maxlen −minlen) withcbeing a constant,the approximation ratio of CSSA is also constant.If we setd=the approximation ratio of CSSA isO(log(maxlen/minlen)),which is similar to [8],[20]and[33].Next,we examine the Rayleigh success probability of each link inSt. Theorem 3.Assume N=0,under the Rayleigh fading model,the Rayleigh success probability of everylink is at least Proof.Without loss of generally,we examine the Rayleigh success probability ofli ∈St ∧li ∈Lm.Letd(ljli) denote the distance betweenlj=(sj,rj)andli=(si,ri).That is,d(ljli)=d(sj,ri).Iljlidenotes the interference ofljonli.Assume thatI=x,under the SINR model,the Rayleigh success transmission probability ofliisWhere,denotes the received power ofri.Therefore,we have, In case ofN=0 and interference being absent,the Rayleigh success probability ofliis always 1 only ifϕ ≥β. Therefore,the Rayleigh success probability ofliis determined by equation (7).Equation (7)shows the impact of the accumulative interference on the Rayleigh success probability ofli.denotes the impact of the interference of thehth layer links onli.Assumeβ=10db,the impact of the interference of thehth layer links is listed in table 1.As shown in table 1,the impact of the 2nd layer links on the Rayleigh success probability may be nearly neglected.We conclude that the Rayleigh success probability ofliis at least 0.9,which is much larger thanAccording to Corollary 4 of[11],Stis a feasible set under the SINR model. Here,we assume that there is always one link transmitting messages,which is reasonable since we need the lower bound of the Rayleigh success probability of every link.Otherwise,the Rayleigh success probability of every link may be larger. Theorem 4.Each link scheduled by CSSA transmits messages successfully with probability1/e in Rayleigh fading model. Proof.Combining Theorem 1 and Lemma 1,we get Theorem 4.In fact,we can directly derive Theorem 4 from Theorem 3. CSSA is very effective for small or medium-sized networks.For a large scale network CSSA is impractical since CSSA needs to collect the information of the nodes and disseminate the scheduling results to the nodes.On the other side,senders residing in the squares with the same number can independently execute the scheduling algorithm.Therefore,we design a distributed square-based scheduling algorithm(DSSA)for senders residing in the same square. The link setLis groupedL1,L2,...,LM.For∀li=(si,ri)∈ Lm,xm≤d(li) ? Figure3.The central point of a square overlaps the origin of coordinates. Before sending a message,senders residing in the same small square use physical carrier sensing technique to compete for the channel.We design a subroutine called sender election algorithm (SEA) to select one sender to send a message.The pseudo-code of SEA is listed in algorithm 2. Each sender can switch its state among three different states,namely,listen state,trasmission stateandhall state.The states switch is shown in figure4. Figure4.State diagram. Time is divided intoθlognrounds,and each round contains 4 time slots.The initial state of the sender waiting for scheduling is set tolisten.In the first slot,the senderswithlistenstate transmits HELLO message with probabilitypfor the purpose of competing for the channel.slistens to the channel in the second slot.At the end of the second slot,ifssends HELLO but does not receive any HELLO message,schanges its state totransmission.In the third slot,if the state ofsistransmission,ssends OMS message to other senders.That is,sinforms other senders that the channel is occupied bys.slistens to the channel in the fourth slot.At the end of the fourth slot,ifsreceives OMS,schanges its state tohall.Afterθlognrounds,thetransmissionstate sender is the winner and elected as the leader of the small square. Note that in the presence of interference,the node will not be able to correctly decode two or more messages.For example,if there are three nodes on a regular triangle transmitting HELLO message simultaneously,none of them will correctly decode each other’s message.In fact,the node will not be required to decode a message correctly,it only needs to know whether the channel is “busy”’ or not based on the channel state information(CSI).That is,if the power level of the channel exceeds the threshold determined by wireless device,then the channel is“busy”,which means that at least one node is competing for the channel. Lemma 3.Finally,at most one sender is in the transmission state.That is,no two senders can transmit messages to their receivers concurrently. Proof.Before transmitting a message,the sendersmust compete for the channel.First,ssends HELLO,then listens to the channel.Ifsdoes not receive any HELLO message (line 12),then it indicates that no other senders compete for the channel withs.On the other hand,oncesoccupies the channel,ssends OMS to other senders and the sender receiving OMS turns its state intohall.To sum up,only one sender occupies the channel. ? Lemma 4.SEA selects a sender in transmission state with a high probability. Proof.Two events lead to the result that SEA does not select one sender in a round.One event is that two or more senders sent HELLO to compete for the channel.The other is that no sender sent HELLO.To sum up,the probability of SEA not selecting one sender in a round is Next,we give a fact as follows. Fact:Given a set of probabilitiesp1,p2,...,pn,pi ∈[0,1/2](i=1,2,...,n),the following inequalities hold: Therefore,we have Afterθlognrounds,the probability of SEA does not select one sender is at most Only ifθis sufficient large. Next,we outline DSSA.We define a notation of Super-Big-Round consisting of 9 Big-Rounds.A Big-Round is comprised of 4θlogn+1 slots.All senders residing in squares labeled 1 execute the SEA algorithm in a distributed way.After 4θlognslots at most one sender in each small square is elected the leader.All leaders send messages to their receivers in the next slot.Then,senders residing in the squares labeled 2,3,...,9 execute SEA,respectively.And,the selected leaders send messages to their receivers.We call this process a Super-Big-Round,which is corresponding to a link class.If there are unscheduled links then DSSA is performed continuously.The pseudocode of DSSA is listed in algorithm 3. Theorem 5.DSSA gives a correct scheduling result. Proof.According to Lemma 3 and Theorem 1,Theorem 5 holds immediately. The correctness of above analysis is based on the assumption ofN=0.In fact,CSSA and DSSA are also correct in case of considering the ambient noise.Next we will discuss that CSSA and DSSA are correct as long as we improve the transmission power.Let the transmission power of a linkl=(s,r)be at least 3βNdα(l).That is,Ps ≥3βNdα(l). ? Lemma 5.Let St denote the set of links transmitting messages in the same slot t.Assume li=(si,ri)∈Lm and li ∈St.The total interference of ri sufferedfrom other nodes in St is bounded by Proof.The analysis is as the same as Lemma 2,so we give the interference bound immediately.The interference ofrisuffered from other nodes inStis Theorem 6.LetThe subsetsreturned by CSSA and DSSA are feasible sets under the exact SINR model. Proof.Without loss of generality,we examineStmentioned in Lemma 5.For∀li=(si,ri)∈St,the SINR value ofriis lower bounded by Therefore,Stis a feasible set. Theorem 7.Considering ambient noise and under the Rayleigh fading model,the Rayleigh success probability of every link is at least Proof.Without loss of generality,we examine the Rayleigh success probability ofli ∈St ∧li ∈Lm.IfI=x,the success transmission probability ofliisThen,we have, From table 1 we can conclude that the Rayleigh success probability ofliis at least 0.96· exp(−1/3)·Whenh<12,the Rayleigh success probability ofliis greater thanIfh ≥12,the influence factors of thehth links can be neglected.According to Corollary 4 of[11]Stis a feasible set under SINR model. In this section,we will compare the efficiency of CSSA and DSSA with three algorithms,named GOU[8],GOW[20]and SLSPC[31].First,from figure5,one can see that CCSA and DSSA achieve almost the same performance under the same setting.If there are unscheduled links in a small square,the centralized algorithm definitely schedules one link;however,the distributed algorithm schedules one link with a high probability.Therefore,the latency of centralized algorithm is slightly better than that of distributed algorithm.For the sake of simplicity,we use SSA as the simulation results of CSSA and DSSA since their performances are almost the same. Figure5.CSSA and DSSA achieve almost the same performance. We examine the latency of SSA,GOU,GOW and SLSPC under the same simulation settings.Assume that the area of the network fieldFis 1500×1500m2,α=3,β=10dbandN=−70db.A link is comprised of two nodes,a sender and a receiver,which are deployed inFuniformly.The minimum length and the maximum length of the links are 1 and 30,respectively.Letd=2,σ=0.4 (for GOW in [20])andε=4(for SLSPC[31])as these settings yield the shortest latency based on the simulations.In DSSA,a sendersneeds to estimate numbercof senders competing for channel,andssends messages with probability 1/(c+1)(line 8 of SEA).In our simulations,we are able to estimate the average number of senders of a small square since the nodes are deployed uniformly,which isWhere,Ssquardenotes the area of a small square andSFdenotes the area ofF.Also note that all the results are averaged over 30 runs. GOU and GOW are two classical algorithms using plane partition strategy.GOU does not consider ambient noise and GOW schedules links under the exact SINR model.From figure6 we can see,SSA (without considering ambient noise) is as better as GOU,and SSA (considering ambient noise) is better than GOW.SLSPC partitions plane into hexagons and considers ambient noise.SSA (without considering ambient noise)is better than SLSPC since SSA does not consider ambient noise.As long as there are unscheduled links in the hexagon,SLSPC always selects one link from the hexagon.However,SSA (considering ambient noise)selects one link to schedule with probability.Therefore,even though there are unscheduled links in the square,none of the links may be scheduled,which leads to a large latency.On the other hand,SSA considers the Rayleigh fading model,which is more practical than the SINR model adopted in SLSPC.Under the Rayleigh fading model,both the power of a received signal and the probability of successfully receiving the signal are random variables.For SSA,we first construct a SINR feasible set.Then,we generate a random value to denote the power of a received signal.At last,the links without satisfying the SINR constraint are removed from the SINR feasible set.Therefore,SLSPC has lower time slots compared with the one of SSA.However,senders compete for a channel in SSA,which is suitable for distributed algorithms and can be applied in large wireless networks. From figure7 we can see that GOW is not sensitive to the minimum length because the number of theblack-graylinks impacts the efficiency of GOW significantly.SSA is the most sensitive to the minimum length since the classification of links and the side length of small squares depend on the minimum length,which determines the scheduling results.Specifically,GOU and GOW partition the network area into squares,of which the side length is related toα,βand the maximum link length of link class.However,the side length is independent of the minimum link length.Therefore,the scheduling results of GOU and GOW are independent of the minimum link length.For SLSPC,the relationship between the number of link groups and the minimum link length is logarithmic while it is linear for SSA.The number of link groups impacts scheduling results.Therefore,SSA is more sensitive to the minimum link length than SLSPC. Figure6.Compare of five algorithms. Figure7.Influence of the minimum length on five algorithms. Along with the increasing of the link length,the received power at the receiver decreases,which results in a reduction in the number of scheduled links.In other words,time slots increase with the increasing of the link length,see figure8.If the maximum link length is larger than 40,many links of GOW areblackgray,which must be scheduled in sequence and lead to large latency.Therefore,GOW has the largest latency. Figure8.Influence of the maximum length on five algorithms.#links=100. Figure9 indicatesαimpacts the efficiency of all algorithms.The side length of the small squares(GOU,GOW and SSA)and the hexagons(SLSPC)is proportional to(1/(α −2))1/α.Note that,2<α <6.The smallerα,the larger the side length.Large side length of squares (hexagons) means the number of squares(hexagons)is small.And,the number of links scheduled in a time slot is also small,since it is related to the number of squares or hexagons.On the other hand,along with the increasing ofα,the interference of the receiver decreases,which leads to an increase of the number of links scheduled in a time slot. Figure9.Influence of α on five algorithms.#links=100. In this paper,parameterddetermines the number of groups of links and the approximation ratio.With the decreasing ofd,the number of groups and the approximation ratio increase.Figure10 shows that the scheduling results are affected by differentds.Ifdis small,the number of groups is big,which leads to large time slots.For example,ifd=3,all links are divided into 10 groups.For the first group of links,the side length of the small rectangle is 28.9 and the number of rectangles is 2,704.Ifd=5,all links are divided into 6 groups.For the first group of links,the side length of the small rectangle is 43.4 and the number of rectangles is 1,225.That is,ifd=3 the 10 groups of links are scheduled separately,while 6 groups of links are scheduled separately ifd=5.On the other hand,ifd=3,we schedule links from about 300 (2,704/9) rectangles in each time slot for the first group of links.However,ifd=5,we only schedule links from about 136(1,225/9)rectangles in each time slot for the first group of links.Therefore,ifdis small (d <17 in figure10),the difference of scheduling results is small.Ifdis large,then the number of groups is small,the side length of rectangles is large and the number of rectangles is small,which leads to the large time slots.Figure11 indicates that SSA obtains a good result ifIn the circumstances,the approximation ratio of SSA isO(log(maxlen/minlen)),which is similar to [8],[20]and[33]. Figure10.Influence of d on SSA.#links=50. In this paper,we study the link scheduling problem under the SINR model and the Rayleigh fading model,and propose two algorithms,CSSA and DSSA.Analysis and simulations show that they achieve a better performance in terms of time delay and capacity than other existing algorithms. Figure11.Compare of performances with the same approximation ratios. However,there are still some challenging problems that have not been solved in this paper.For example,we assume that nodes are uniformly deployed in the network field,while ignoring the fact that there are many nodes in a local field.As a result,some stages will be prolonged and the time delay of the remaining nodes is enlarged.In addition,the rate of successful transmission scheduled is a bit low.We will solve these problems in our future work. ACKNOWLEDGEMENT This work was supported by NSF of China under grants 61672321,61771289,61832012 and 61373027,MBRP of Shandong Provincial Natural Science Foundation under grant ZR2019ZD10,STPU of Shandong Province under grant J15LN05.This work was supported by NSFC under grants 90718030,and 90818002.IV.SCHEDULING ALGORITHM
4.1 Group Links
4.2 Partition Network Region
4.3 Centralized Square-based Scheduling Algorithm

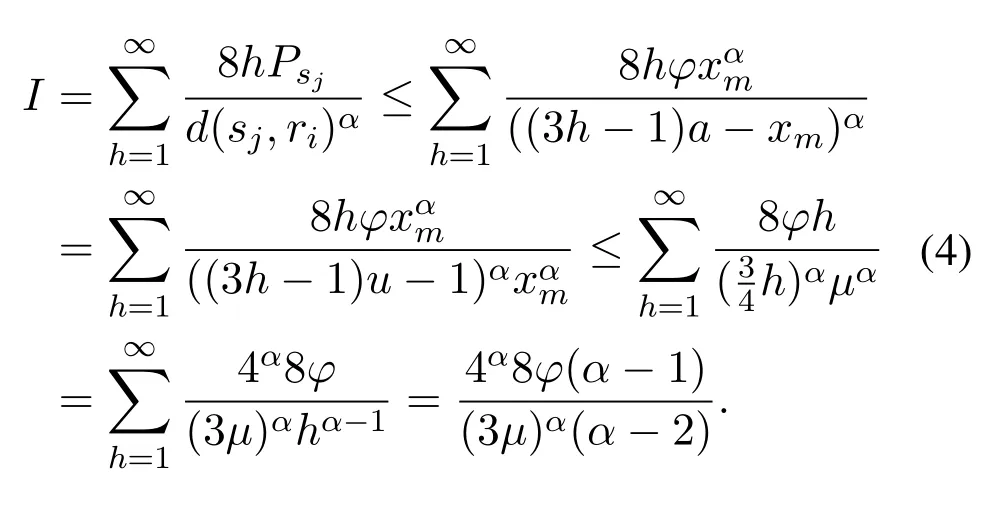
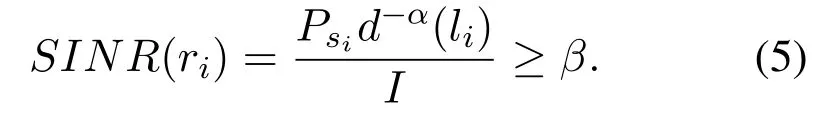
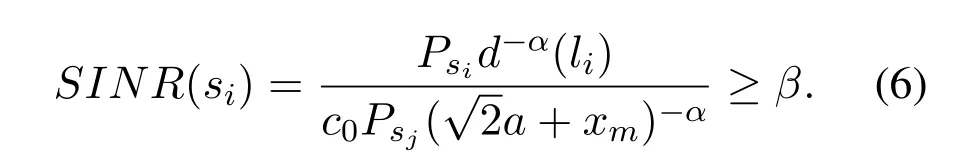
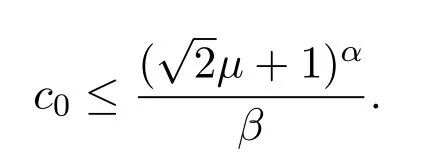
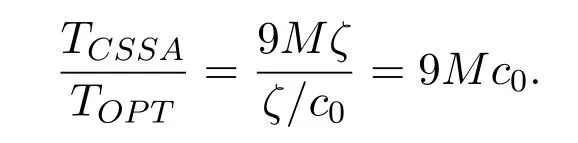
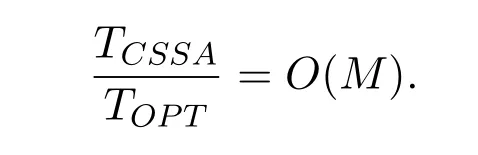

V.DISTRIBUTED SQUARE-BASED SCHEDULING ALGORITHM
5.1 Outline the Algorithm DSSA

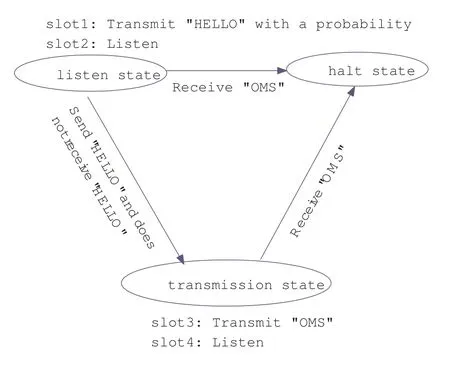

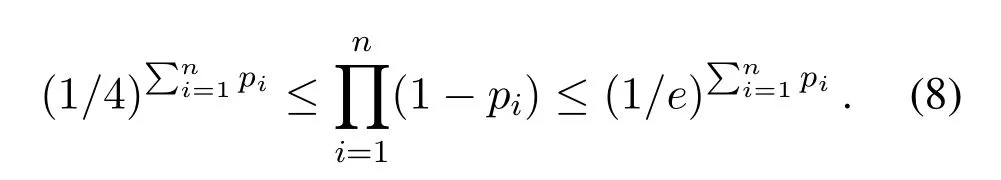
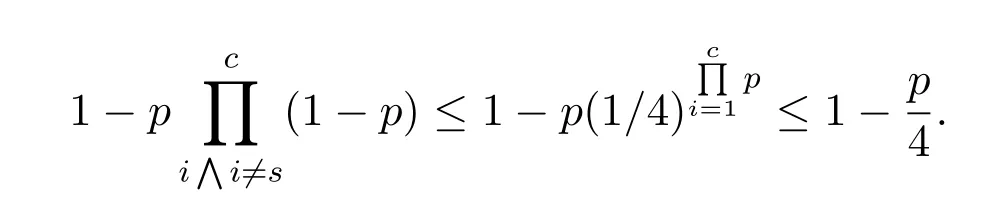
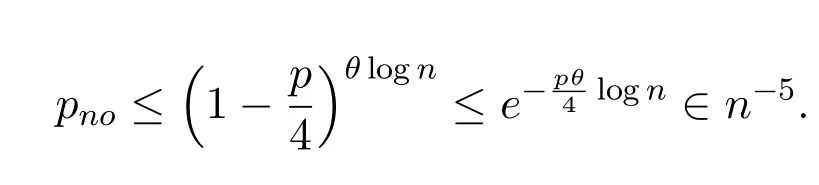
VI.THE IMPACT OF AMBIENT NOISE

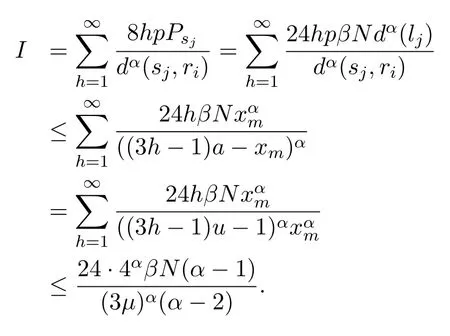
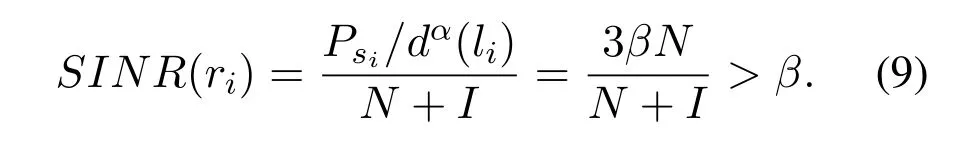
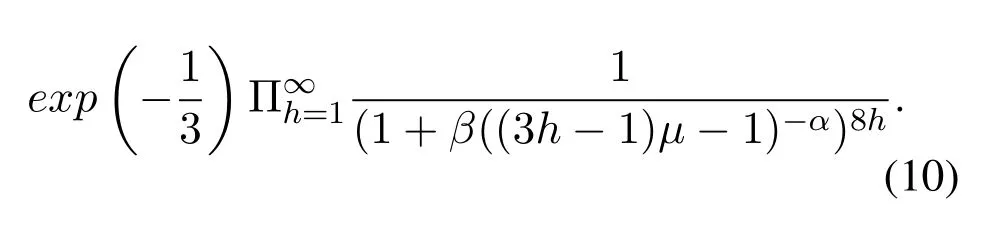
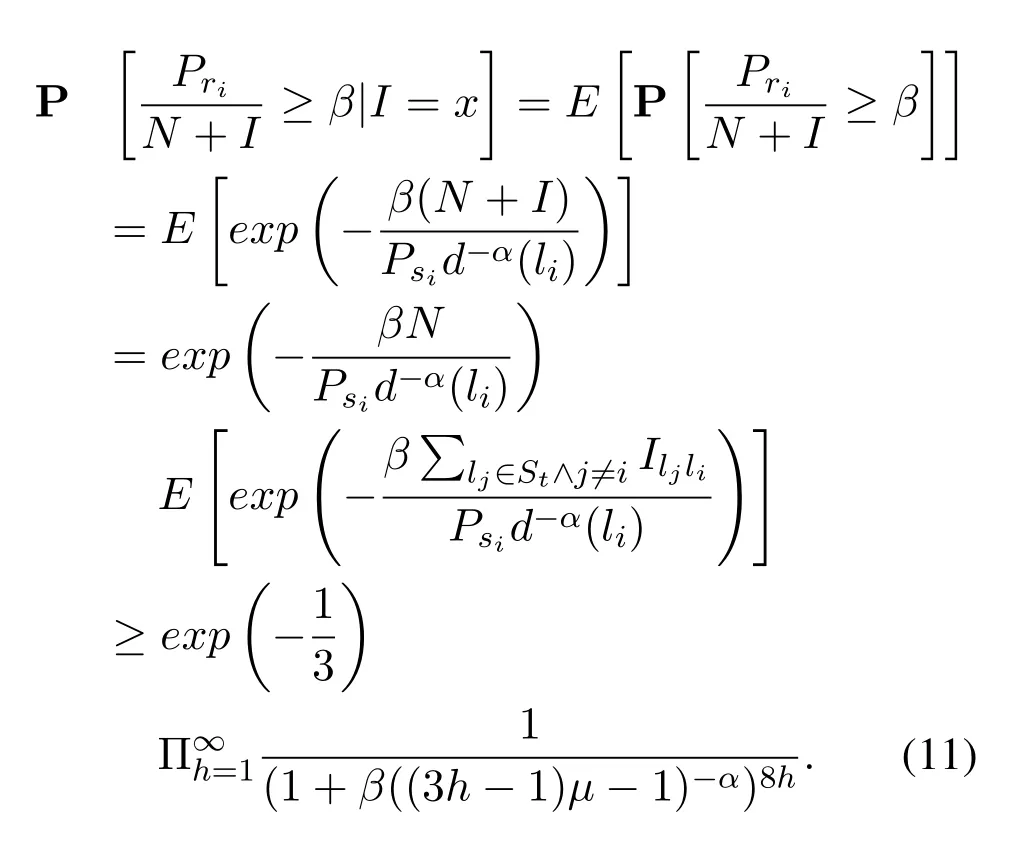
VII.SIMULATIONS AND ANALYSIS
7.1 Simulation Settings
7.2 Simulation Results
VIII.CONCLUSION AND OUTLOOK