Precoder Design and Impulsive Noise Mitigation Scheme for Industrial Wireless Communications

Yanjing Sun,Xinyan Li,Jiasi Zhou,Ruirui Chen,Bowen Wang,Yanfen Wang

1 School of Information and Control Engineering,China University of Mining and Technology,Xuzhou 221008,Jiangsu,China

2 Xuzhou Engineering Research Center of Intelligent Industry Safety and Emergency Collaboration,Xuzhou 221008,Jiangsu,China

Abstract:In industrial wireless scenarios,the impulsive noise (IN) incurred by machine running or operation causes a serious influence on the powerlimited industrial wireless communications.It is challenging to ensure efficient and reliable transmission with quality of service (QoS) guarantee for machinetype communication devices (MTCDs).Considering the IN in the industrial process,this paper establishes the multiuser multiple-input single-output(MU-MISO)orthogonal frequency division multiplexing (OFDM) system model,which combines transmitter and receiver design.Two precoding schemes are designed to improve communication effectiveness at the transmitter.More specifically,the precoder design scheme which combines semi-definite relaxation (SDR) with difference-of-two-convex-function(D.C.) iterative algorithm,is developed by utilizing the Dinkelbach method to improve the system effectiveness.To decrease the computational complexity,we devise the quadratic-based fractional programming(QFP)algorithm,which decouples the variables by using a quadratic transform method.On this basis,the IN mitigation scheme is studied to reduce the system error rate (SER) at the receiver.With the goal of improving the reliability of industrial wireless communications,we propose a hybrid nonlinear IN mitigation(HNINM)scheme and then derive its closed-form expression of SER.The simulation results show that the proposed QFP algorithm achieves superior performance while the HNINM scheme decreases the SER of industrial wireless communications.

Keywords:Industrial wireless communications;precoder design;impulsive noise mitigation

I.INTRODUCTION

As the rapid rise of fifth-generation cellular access(5G)technology and the introduction of the Internet of Things (IoT) concepts,industrial wireless communications have been brought to the fore[1,2].However,the harsh industrial environments make it challenging to guarantee the required quality of service for different applications.In the industrial IoT with massive access devices,the mechanical equipment will radiate abundant electromagnetic noise due to the broad temperatures,strong vibration,spark discharge,and other physical phenomena during operation[3].Typical 5G based industrial wireless communications scenarios,including factories,mines,steel,power,ports,etc.,are affected by noises generated by heavy machinery,frequency converters,electric switches,and so on [4–6].The noise with extremely short pulse duration and high pulse power is randomly generated,which can be characterized by the impulsive noise(IN)model.Simultaneously,it shows a higher power spectral density(PSD)than the background noise.Owing to these characteristics,IN will cause bit or burst errors of communication system,which leads to a significant deterioration of data transmission reliability and communication quality [7,8].The influence of IN is the bottleneck of implementing high speed and reliable industrial wireless communications systems.

1.1 Related Work and Motivation

Orthogonal frequency division multiplexing(OFDM),as a highly-effective multi-carrier transmission technology for high data rate wireless applications,is widely used in industrial wireless communications[9].Although ultramodern multi-access technologies,such as non-orthogonal multiple access(NOMA),are emerging,the complex transmitter design and the negative impact of multi-user interference make them unsuitable for industrial wireless scenarios.Meanwhile,compared with single-carrier system,OFDM system has stronger robustness to multipath fading [10,11].Although OFDM systems are robust against fading and interferences,it is sensitive to noise with significant IN[12].Existing industrial wireless communications technologies,such as LoRa,NB-IoT,WiFi,BlueTooth,etc.,are mainly utilized in OFDM systems[13,14].More performance analysis for OFDM communication system in industrial wireless scenarios has been investigated in[15–22].In[15],the authors studied achievable receiving rate of multiple-input multiple-output(MIMO)-OFDM underwater acoustic communications.The authors in [16]proposed a receiver design improving channel capacity for MIMOOFDM visible light communication system.In [17],the authors analyzed the spectral efficiency and energy efficiency of the improved unmanned aerial vehicle (UAV)-OFDM communication system.However,the above works only consider performance analysis of OFDM system with additive white gaussian noise(AWGN).Actually,when we study the communication performance for OFDM system,IN cannot be neglected due to its high energy and destructive effect on reliable communication [18,19].In [22],a precoder design scheme was developed to maximize the system throughput for a power line communications(PLC)system.The authors in[20]proposed an effective precoding scheme of the PLC network to satisfy the target transmission rate and minimize the cost of each user.The work in[21]investigated the throughput of the OFDM-based smart grid to analyze the impact of IN on the performance of the communication layer.However,most of the above work only studies the optimization of communication efficiency,but does not consider the impact of IN on reliability.

As mentioned above,due to the universality of IN in industrial wireless scenarios and the vulnerability of OFDM system to excessive IN,anti-IN receiver design has become another research hotspot in industrial wireless communications.Since the characteristics of IN deviate drastically from AWGN,the traditional receiver design in the AWGN environment is not suitable for the IN circumstance.In [23],Xinrong et al.proposed a joint channel impulse response estimation and IN mitigation method based on compressed sensing theory,which does not require other prior information of channels and noise.The authors analyzed IN mitigation algorithm based on the least-squares formulation in [24]for the underwater OFDM system.Nevertheless,due to the high computational complexity and processing delay,the above algorithms make strict demand on OFDM system,which is not practical for industrial wireless communications.Some related work investigated nonlinear IN mitigation schemes.The authors in [12]proposed a blanking nonlinearity scheme to study the performance of OFDM system with IN and derive the closed-form analytical expressions of the output signal to noise ratio (SNR).The results in [12]were extended in [25]by proving the Lyapunov stability of nonlinear iterative interference cancellation techniques for OFDM signals with blanking nonlinearity in IN channels.In [26],the authors proposed an iterative successive interference cancellation scheme to overcome the inter-carrier interference of nonlinear blanking IN mitigation.It was shown in[27]that a deep clipping scheme was presented to mitigate the IN.The nonlinear IN mitigation schemes have been widely used in industrial wireless communications owing to its high efficiency and simple implementation.

Since reliability and effectiveness are not guaranteed at the same time in the research of communication performance in general.The above works on industrial wireless communications are only concerned with improving efficiency or reliability.Furthermore,in practical industrial wireless scenarios,due to limitations of device size,hardware design complexity,and energy consumption (such as drones,low-power wireless sensors,and small IoT devices,etc.),it is impossible to place a large-aperture antenna array on machine-type communication devices (MTCDs),and only a single antenna can be set up.Due to the above facts,we thus study effective and reliable communication for the multiuser multiple-input single-output(MU-MISO)-OFDM system,which is based on the joint transmitter and receiver design.

1.2 Main Contributions

As discussed above,most related works on industrial IoT with massive connected devices suffer from two major issues,as follows:firstly,the impact of IN on communication quality is ignored;secondly,they only consider reliability or communication efficiency alone.With this issue in heart,we propose an industrial wireless communications framework designed by the joint transmitter and receiver that considers the impact of IN to realize an efficient and reliable communication system.On this basis,we investigate the precoder design and system error rate (SER) of the OFDM system in power-limited industrial wireless communications.Two precoders are designed to maximize energy efficiency with quality of service (QoS)for MTCDs constraints.After that,the noise mitigation scheme is elaborately designed to improve the reliability of industrial wireless communications.The contributions of this paper are concluded as follows.

• Considering the impact of the transmit diversity of the MISO system and the multi-carrier transmission of OFDM technology on the reliability and effectiveness of data transmission,we establish an MU-MISO-OFDM system model of the joint transmitter and receiver for industrial wireless communications scenarios with IN.

• To overcome the non-convex fractional programming problem caused by precoding vector coupling,we proposed a framework that combines the Dinkelbach method and convex optimization to reconstruct the original problem into a two-tier alternating problem.After that,closedform expression is used to solve the outer layer,and the inner layer is transformed into a convex form by employing a difference-of-two-convexfunction(D.C.)algorithm.

• To reduce the computational complexity,a twotier alternating quadratic transform framework is proposed to reconstruct the formulated precoder design problem,which applies the multiple-ratio quadratic transform and the single-ratio quadratic transform to separate the receiving rate and the formulated energy efficiency maximization problem.By two-tier quadratic transform,the original problem is transformed into a convex optimization problem,which can be solved effectively.

• To reduce SER of industrial wireless communications,a blanking and clipping based IN mitigation scheme is developed to achieve reliable communication.Furthermore,we derive the closed-form expression of the SER after IN mitigation.

1.3 Organization and Notation

The rest of this paper is organized as follows.In Section II,we describe the system model,the noise model and problem formulation.For the formulated problem,two precoder design schemes are proposed in Section III.In Section IV,we develop an IN mitigation scheme.Numerical results are provided to demonstrate the proposed algorithms performance in Section V.Finally,the conclusion is drawn in Section VI.Notations:AH,Tr(A)and Rank(A)denote Hermitian transpose,trace and rank of matrix A,respectively.|A|refers to the determinant of matrix A.A ≽0 denotes that matrix A is a positive semidefinite matrix.Re(b) represents real part of vector b.‖b‖refers to its Euclidean norm.

II.SYSTEM MODEL AND PROBLEM FORMULATION

2.1 System Model

In this paper,we consider an MU-MISO-OFDM system in power-limited industrial wireless communications scenarios,including a base station(BS)equipped withMantennas andNsingle-antenna MTCDs,respectively.LetN={1,2,···,N}denote the MTCD index set.Denote hn ∈CM×1and wn ∈CM×1as the channel gain vector and precoding vector of then-th MTCD,respectively.Thus,the signal received by then-th MTCD can be expressed as

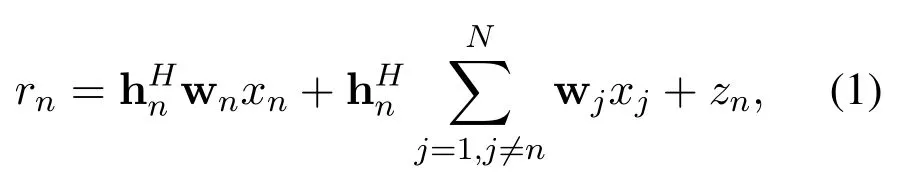
wherexnrepresents the transmitted signal of then-th MTCD,and the signal power is normalized asσ2x=znis the noise signal combining I N and background noise.

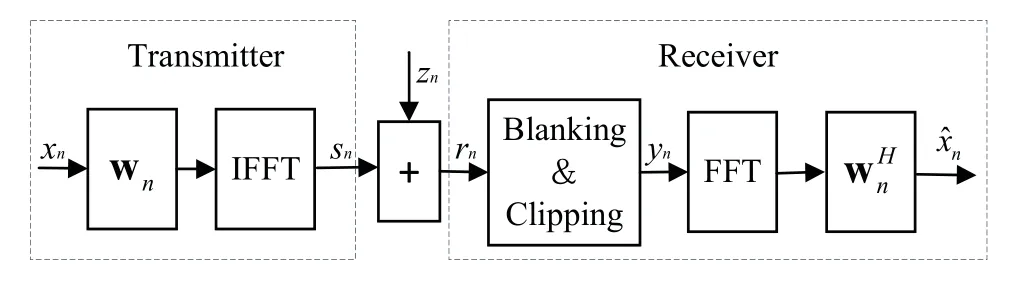
Figure1.Precoder design and impulsive noise mitigation scheme for the n-th machine-type communication device.

2.2 Noise Model

To analyze the effects of IN on industrial wireless communications,background noisezgis generally modeled as Gaussian complex random variables with zero-mean andσ2g-variance.Impulsive noiseziincurred by machine running or operation is usually modeled as Middleton Class A (MCA) noise model in general because the IN is narrow-band in the considered industrial wireless communications scenario[5,6].Its amplitude probability density function(PDF)is written as Eq.(1)in[28,29].

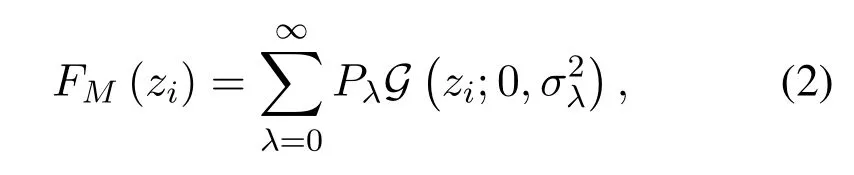
where 0≤λ≤Φ signifies the noise state and Φ→∞is the total state number.Pλ=Ωλe−Ω/λ! is the probability of IN occurrence in stateλ.G(zi;0,σ2λ)refers to as Gaussian PDF with zero-mean andσ2λ-variance.According to Eq.(2),the MCA model assumes that the IN generated by different interference sources follows the Poisson distribution in time,and

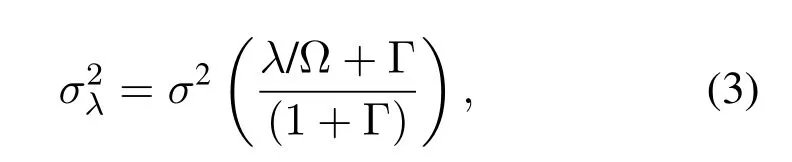
whereσ2=σ2i+σ2gand Γ=σ2g/σ2i,σ2iis the IN power andσ2gis the AGWN power.Γ represents the ratio of AGWN powerσ2gto IN powerσ2i.Ω≤1 shows the impulsive index.Afterwards,the Bernoulli-Gaussian distribution[30]is used to simulate the noise distribution of the industrial wireless communications system in different states.

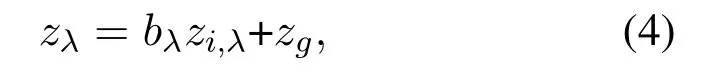
wherebλis a Bernoulli random variable with parameterp=Pr(b=1).It represents the frequency of IN occurrence.zλandzi,λrepresent total noise and IN in stateλ,respectively.

2.3 Problem Formulation

We can rewrite the precoding vector of then-th MTCD in stateλas wn,λ ∈CM×1,then the received signal can be expressed as

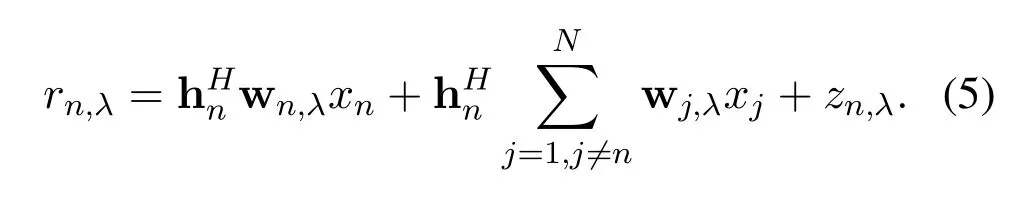
Since the receiving power is affected by noise and transmission power,when the transmission power is a fixed value,the receiving power in each state is different.Assuming that the transmitter obtains the channel state information of all devices[31]and the interfering link follows Rayleigh fading[32].In the following,we take the procedure of transmittingxnin the industrial wireless communications system as an example to derive the precoding vector for stateλ.Then in stateλ,the signal to interference plus noise ratio(SINR)of then-th MTCD can be described as

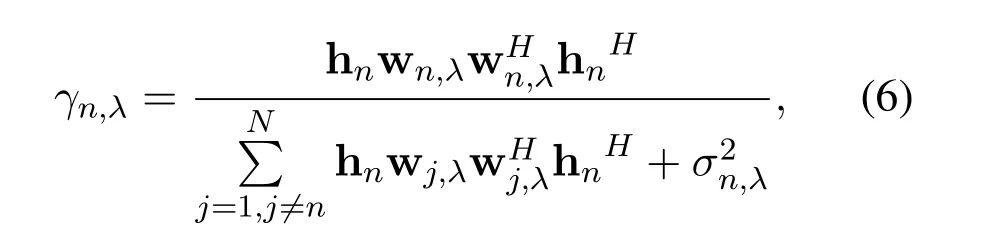
whereσ2n,λis the noise power including IN and AGWN in stateλ.The achieved receiving rate of then-th MTCD in this state is

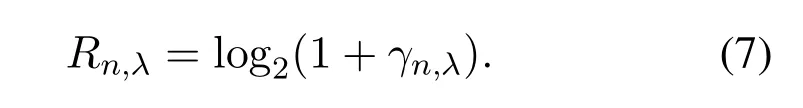
The circuit power consumption of a communication system usually depends on the power consumption of transmit modules including digital signal processing,frequency synthesizers,and mixers.To simplify the processing,it is quantized as a fixed constant,denoted bypc.The total power consumption of BS forNMTCDs is

In this paper,we investigate the precoder design problem for the power-limited industrial wireless communications system to maximize energy efficiency subject to the QoS of MTCDs.We useηλto represent the energy efficiency of the system,which is defined as

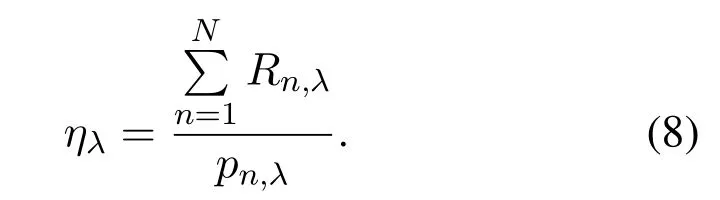
The precoder design problem can be expressed as

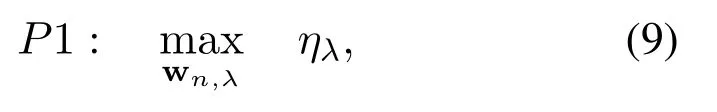
wherepmaxandγn,minrepresent the maximum transmission power and minimum SINR of each MTCD.Eq.(9a)is the energy resources constraint and Eq.(9b)shows the MTCD QoS restriction.

It is worth mentioning thatP1 is a non-convex fractional programming problem,since Eq.(9) and the left side of each constraint in Eq.(9b),which are in fractional form,contain mutually coupled precoding vectors,thus being a non-convex function in general.Hence,the optimal solution toP1 is generally challenging to obtain.In the next section,we develop a convex optimization based design framework for solvingP1.

III.PROPOSED ALGORITHMS

In this section,we mainly propose two precoding design schemes,namely,joint SDR and D.C.iterative algorithm and Quadratic-based fractional programming algorithm.Specifically,by exploiting the fractional structure ofP1,we establish Dinkelbach-based and quadratic-based reformulations ofP1,which can be solved by applying powerful algorithms in convex optimization.

3.1 Joint SDR and D.C.Iterative Algorithm

Since non-convex fractional programming is extremely challenging to solve,we first embrace SDR algorithm to relaxation.Let Hn=hnhHnand Wn,λ=wn,λwHn,λ,P1 can be recast to subject to

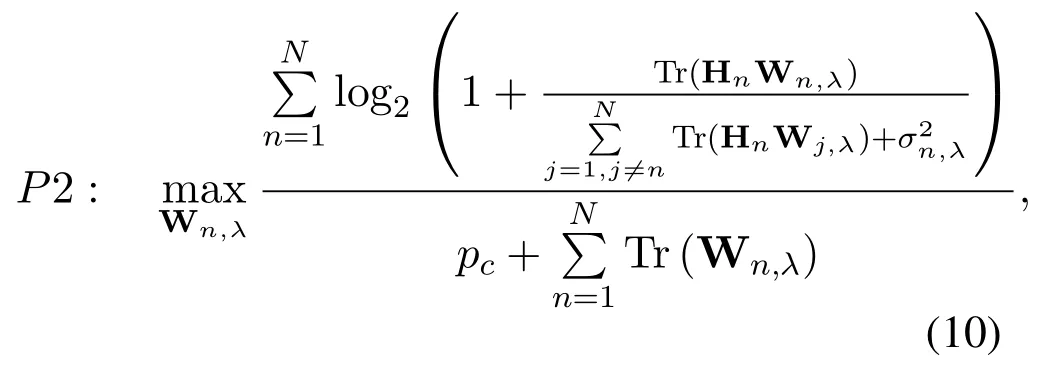
subject to

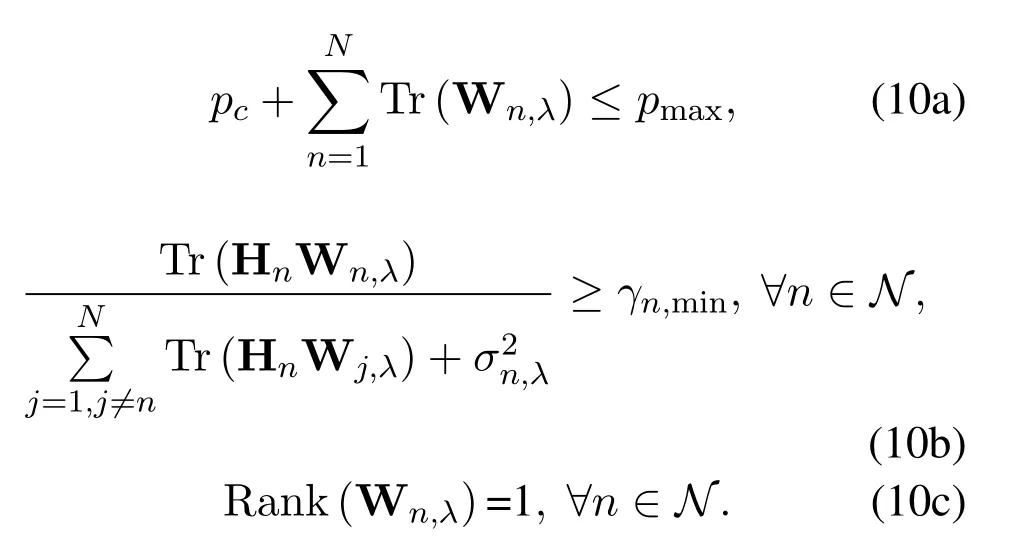
where the constraint Eq.(10c) is imposed since Wn,λ=wn,λwHn,λand Rank(AB)≤min(Rank(A),Rank(B)).

P2 is still a non-convex fractional programming.With the goal of making it tractable,we introduce nonnegative arbitrary variables tλ=[t1,λ,···,tn,λ]to transform the denominator of the optimization objective.Afterwards,Eq.(10)is converted to

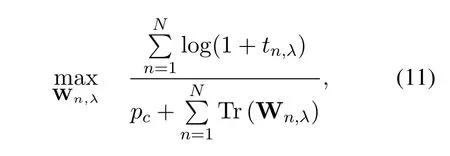
and the non-convex constraints Eq.(10b)can be transformed into

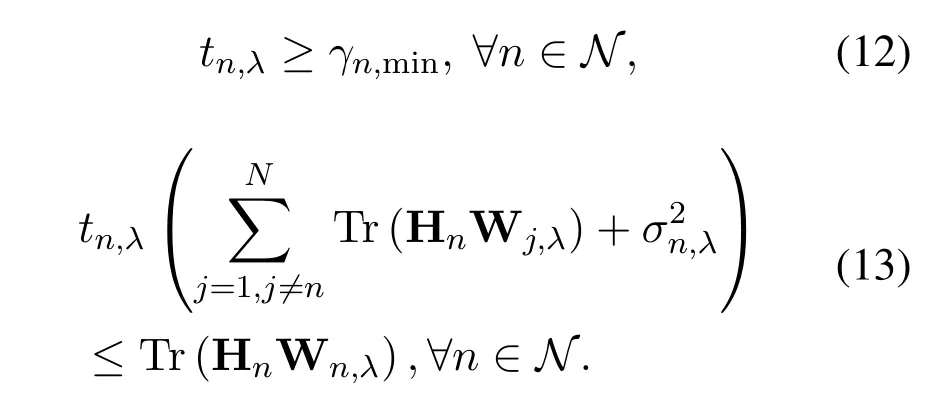
Owing to the fractional form of Eq.(11),the optimization objective is hard to solve.To simplify the objective function,variableµλis introduced to divide the optimization objective into simple optimization objective and fractional constraint,which is

After that,we adopt Dinkelbach algorithm [33]to reformulate the constraint Eq.(14) by introducing a non-negative arbitrary variableyλ.Eq.(14) changes from a complex fractional constraint to a convex constraint,which is

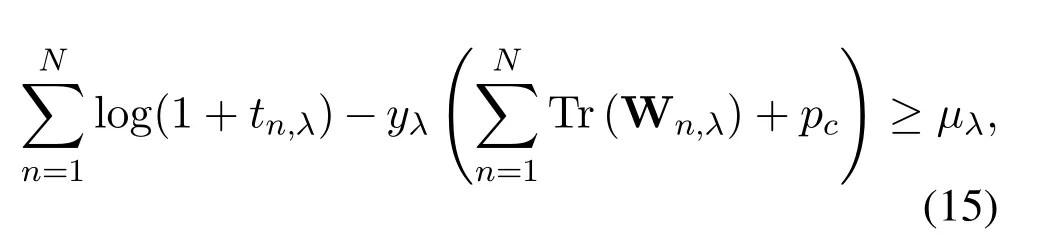
where

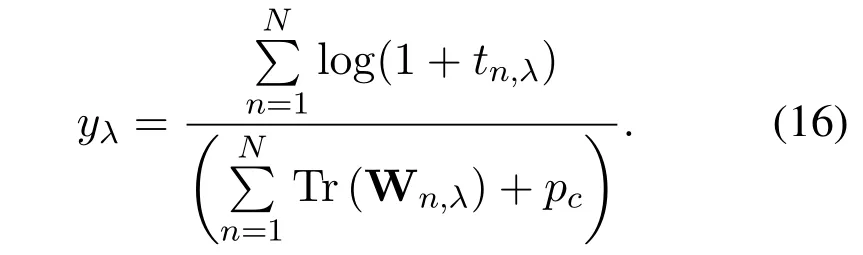
Due to the mutual coupling of the introduced variable tλand the precoding vector,the pivotal coupling constraint Eq.(13) is not a convex constraint.It can be divided into a D.C.function and a convex restraint by properly introducing a new arbitrary variable

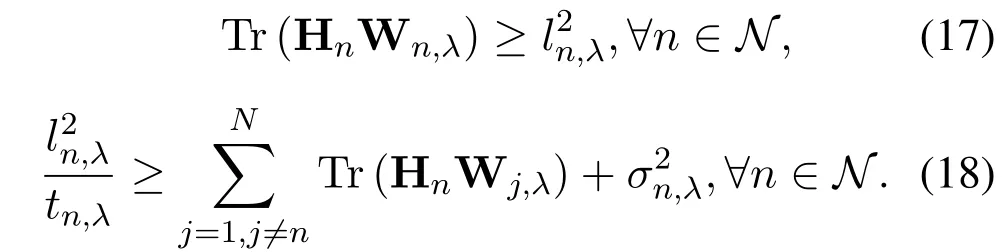
In virtue of the D.C.constraint condition,the left hand of Eq.(18)is approximated by its first-order Taylor expansion,which is represented as

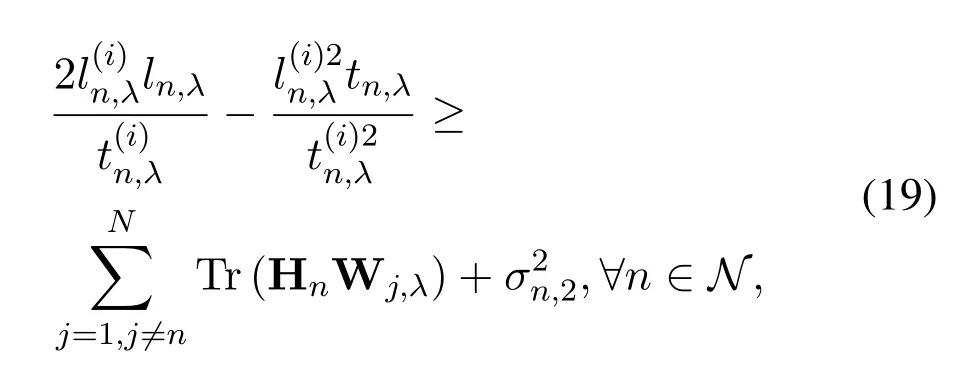
whereiis the iteration index.

Based on the above processing,the constraints ofP2 are all convex except Eq.(10c).P2 has hardship in sloving directly because of the rank-one constraint.To facilitate the solution,we slack the constraint Eq.(10c)by adopting rank-one relaxation.P2 can be recast as

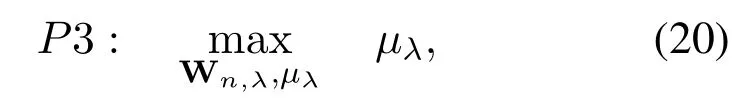
subject to

?

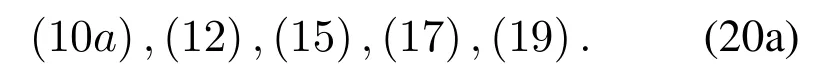
Whenyλis fixed,P3 is a standard convex optimization problem which can be solved by off-the-shelf solvers.Since we ignore the rank-one constraint on the original problem,the optimal solution ofP3 is not equivalent toP2.If and only if the optimal solution ofP3 satisfies rank-one,P3 is equivalent toP2.We demonstrate that the optimal solution ofP3 satisfies rank-one in Appendix A.The detailed algorithm is shown in Algorithm 1.

Then,we evaluate the complexity and convergence of algorithm 1 analytically.

Complexity:Note that the complexity for traditional inner point method withKvariables is O(K3.5)[34].In the above algorithm,the number of variables isM2+ 2N+ 1,whereMandNare the number of antennas and MTCDs at the transmitter,respectively.It contains two layers of loops.Hence,the overall complexity iswhereφ2andφ1respectively represent the average number of iterations of the inner and outer loops.

Convergence:For the joint SDR and D.C.iterative algorithm,its convergence needs to prove the convergence of the inner-layer D.C.algorithm and the outerlayer Dinkelbach algorithm,respectively.Similar to the detailed proof of [35],it is easy to obtain the algorithm can converge to a local optimum after a finite number of iterations,where the proof is omitted for brevity.

3.2 Quadratic-based Fractional Programming Algorithm

The formulated energy efficiency optimization problem involves multiple-ratio fractional planning.However,using Dinkelbach algorithm to deal with multiple-ratio fractional problem is scarcely equivalent to the original problem in most cases.After utilizing Dinkelbach method,to dispose of multiple-ratio fractional problem in numerator ofP2,the proposed joint SDR and D.C.iterative algorithm separate it into a series of convex constraints.Hence,it contains the outer Dinkelbach algorithm and the inner D.C.iteration,which makes it have high computational complexity and slow convergence speed,especially when the numbers of MTCDs and BS antennas are large.

In the following,we develop a Quadratic-based fractional programming (QFP) algorithm to reduce the computational complexity based on the work presented in [36].In the proposed QFP algorithm,to makeP1 tractable,we apply the quadratic transform to handle the multiple-ratio SINR of its numerator and the whole optimization goal,and convert it into a convex optimization problem.

Similar to the joint SDR and D.C.iterative algorithm,arbitrary variables tλ=[t1,λ,···,tn,λ]is introduced.Eq.(9)is relaxed as

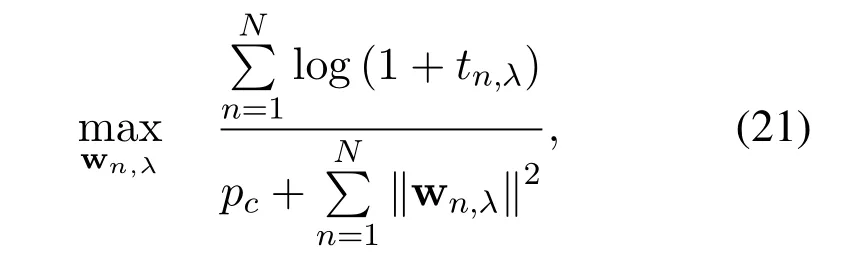
and we can obtain the constraint Eq.(12)and

Next,we introduce variableµλto further transform the fractional form of Eq.(21)and get

?

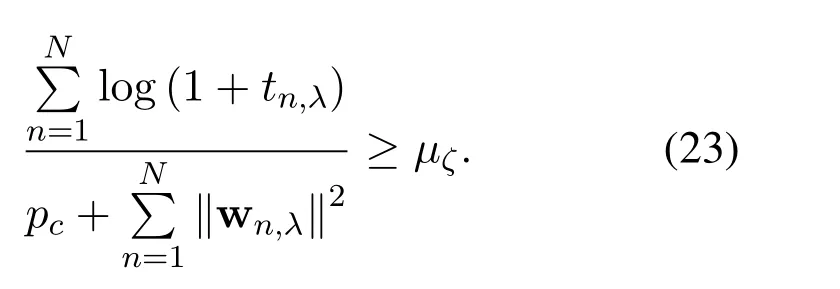
After that,the multidimensional quadratic transform is used to handle the left hand of constraint Eq.(22),which is a non-convex function,to simplify the fractional function.Arbitrary variable yλ=[y1,λ,···,yn,λ]is introduced to convert Eq.(22)into a series of convex constraints.

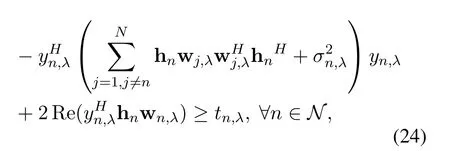
where

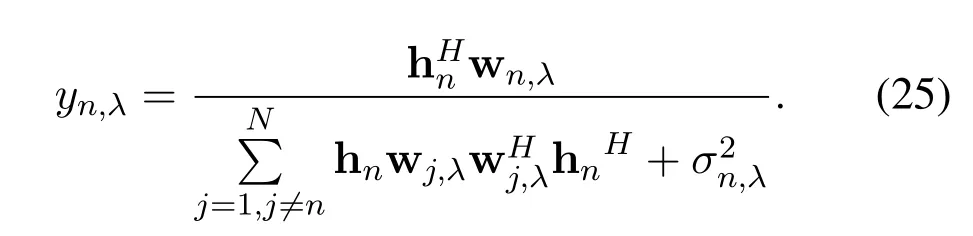
Then,the single-ratio quadratic transform is adopted to deal with Eq.(23).Non-negative arbitrary variablezλis introduced to convert the complex fraction constraint Eq.(23)into

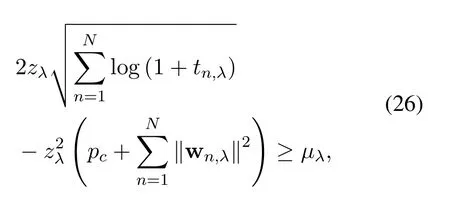
where

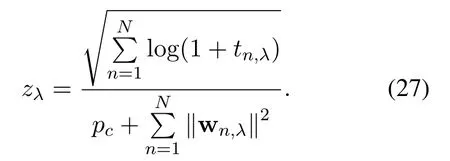
According to the above analysis,P1 can be recast as

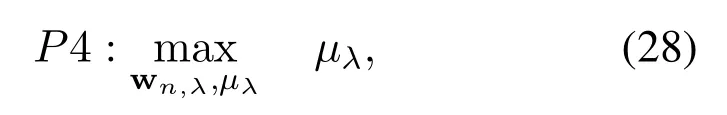
subject to

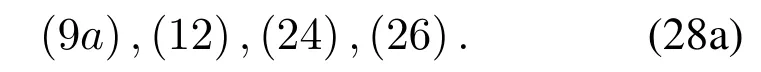
P4 is a standard convex optimization problem whenzλand yλare both fixed.Therefore,it can be solved with a standard convex solver.The detailed iterative procedure is summarized in Algorithm 2.

Complexity:In algorithm 2,the number of variables isM+N+1,and the complexity is(M+N+1)3.5.The complexity of the QFP algorithm is significantly lower than the joint SDR and D.C.iterative algorithm.

Convergence:The convergence of QFP algorithm is similar to the outer algorithm of joint SDR and D.C.iterative algorithm and the proof is also omitted for the limiting space[37].

IV.IMPULSIVE NOISE MITIGATION

The precoding scheme can improve the communication efficiency of the system by suppressing multi-user interference,but it cannot alleviate the impact of IN on the reliability of the communication system.Next,an OFDM-based system with IN mitigation is investigated in this paper.At the transmitter,the precoded signal is mapped to baseband symbols by quadrature amplitude modulation (QAM).Ncomplex baseband symbols within a symbol interval are converted by inverse fast Fourier transform(IFFT)to obtain complex baseband OFDM symbols.At the receiver,when IN energy is excessive,it propagates among simultaneously transmitted OFDM subcarriers by fast Fourier transform (FFT) demodulation process,which gives rise to severe degradation of industrial wireless communications performance.Therefore,before the traditional OFDM demodulator,a hybrid nonlinear IN mitigation(HNINM)module is devised to process the precoded signal,which has gone through the precoding design and channel fading.It can mitigate the effect of IN,which is based on the known statistics information of IN and the noise model.

Figure2.Hybrid nonlinear impulsive noise mitigation scheme.

The HNINM scheme can limit the received signal to a predetermined amplitude range while maintaining the same phase.Specifically,as shown in Figure2,the HNINM scheme has two amplitude thresholds,namely the clipping thresholdT1and the blanking thresholdT2.Making|rn|to represent the amplitude of the received signal,we analyze three cases of the received signal in HNINM scheme.When|rn|≤T1,the received signal is regarded as transmitted signals without affected by noise.IfT1≤|rn|≤T2,we clip the received signal and set the signal amplitude as the threshold with the phase compensation factor.While|rn| ≥T2,the received signal is considered as IN and its amplitude is set to zero.Summarily,the output signal of the HNINM scheme can be expressed as

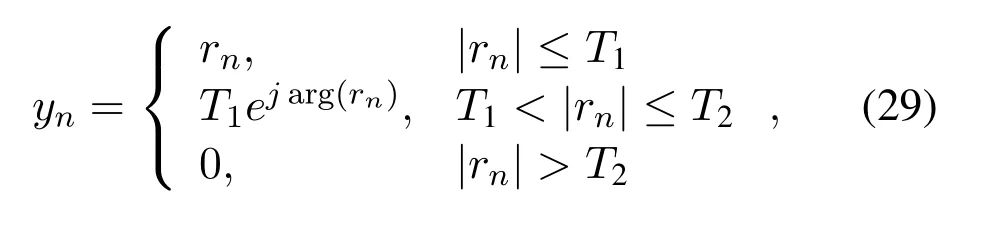
whereT2=aT1.

The output signal of the nonlinear noise mitigation scheme can also be expressed as

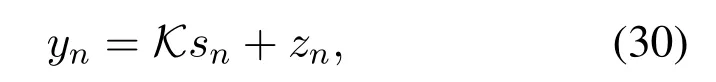
whereKis a scale factor,and its specific form is given by

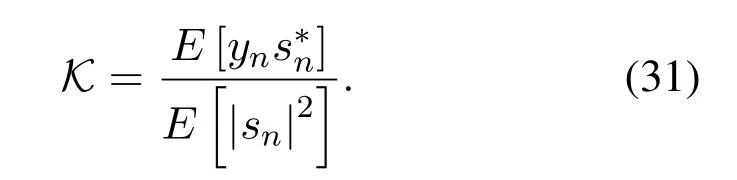
According to [12],the output SNR after HNINM scheme can be given by

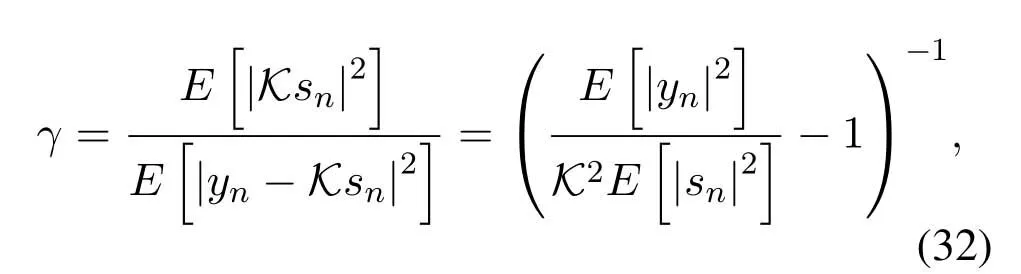
whererepresent the precoded OFDM signal power and the total signal power at the output of nonlinearity.Their explicit expressions are given by Eq.(33)and Eq.(34),respectively.

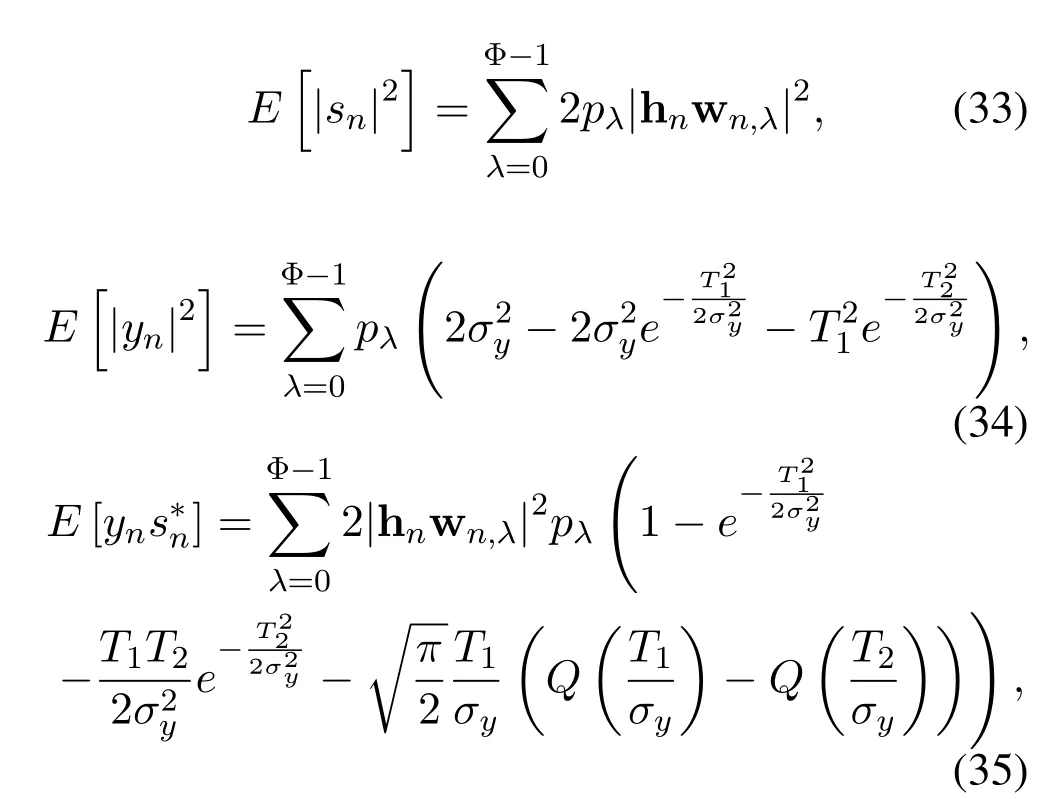
whereis the occurrence probability of the stateλ.Q(x)is the GaussianQ-function [38].The derivation of Eq.(33)-Eq.(35)will be considered in Appendix B.

The SER of OFDM system is given by

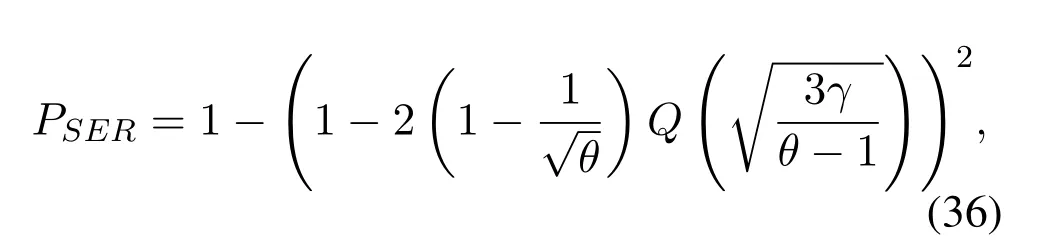
whereθis the constellation order,γis the output SNR after HNINM scheme.

V.SIMULATION RESULTS

In this section,the performance evaluation of the proposed algorithm was carried out using Matlab simulations.The channel model is not determined in the practical industrial scenario.To simplify the analysis,this paper assumes that the channel coefficients between the transmitter and receiver are modeled as independent and identically distributed Rayleigh fading.The 16-QAM is adopted to modulate input signals for the OFDM system with 256 subcarriers.The parameters used in the simulations are summarized in Table1.Consorting to the work presented in[12],in the following simulation,we choosea=1.4.Furthermore,we use two benchmark algorithms to evaluate the proposed HNINM scheme.The first benchmark algorithm is the blanking algorithm in [12],and the second algorithm is the clipping algorithm in[11].In this article,we only investigate the above two benchmark algorithms for the pre-coded signal designed by the QFP algorithm for simplicity.

In Figure3,we compare the energy efficiency of the two precoding algorithms under different noise states.This simulation selects four noise states.It can be noticed that the energy efficiency of the system is the largest when the noise state is zero and it becomes smaller with the increase of the noise state number.The reason is that as the number of noise states increases,the IN power increases and the probability of occurrence decreases,resulting in a sharp drop in en-ergy efficiency.When the number of noise states is greater than 3,the energy efficiency is close to zero.Considering the complexity of the simulation and its small impact on energy efficiency,we ignore this situation.Besides,it can be clearly seen that the performance difference between the two precoding algorithms is very small,which shows that both algorithms can better solve the problem of energy efficiencybased precoder design in IN environment.Particularly,the simulation results show that when SNR is small,the performance of joint SDR and D.C.iterative algorithm (denoted as SDR in the simulation diagram for simplicity)is better than that of the QFP algorithm.

Table1.simulation parameters setting.

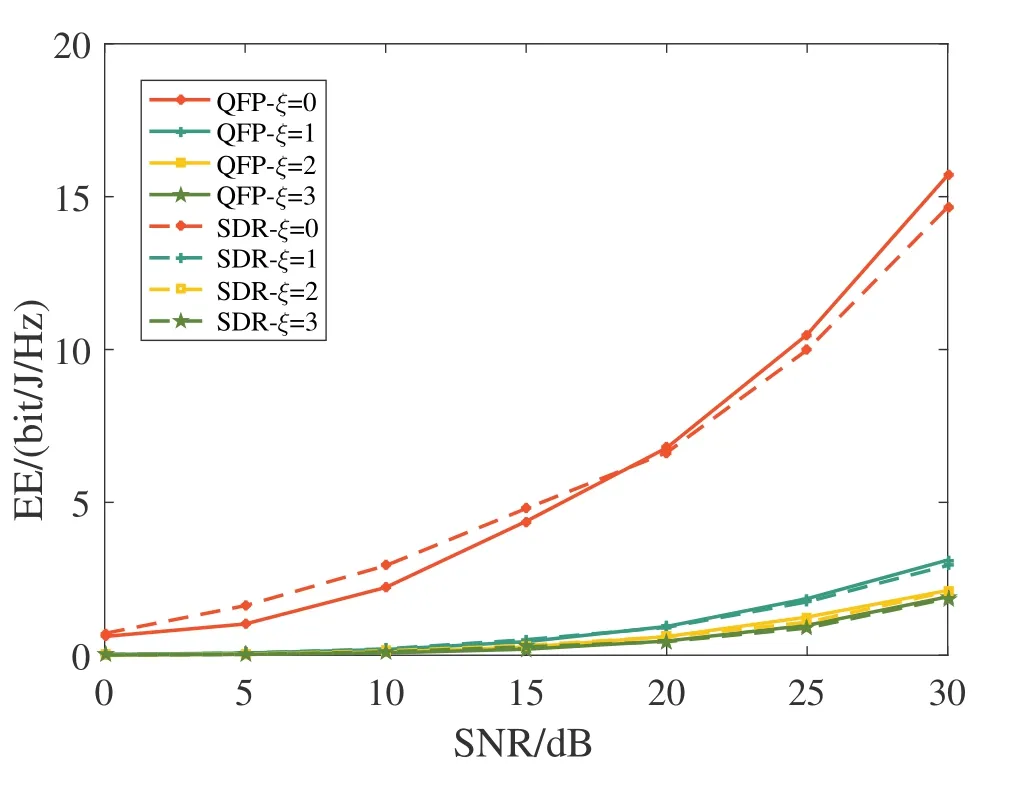
Figure3.Energy efficiency versus the SNR under different noise states of two precoding algorithms.

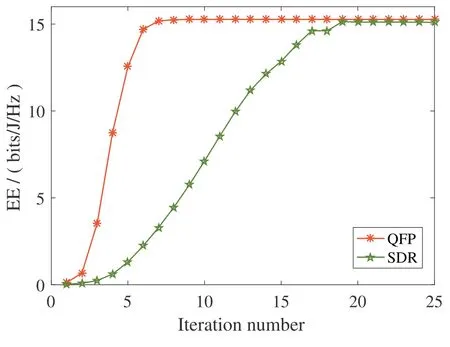
Figure4.Convergence performance of our proposed iterative algorithms with zero noise state.

Figure4 compares the convergence speed of two different precoder design algorithms when the noise state is zero.It is obvious that both the joint SDR and D.C.iterative algorithm and the QFP algorithm converge to a steady value after finite iterations,which also validates the previous convergence analysis.We also notice that the convergence speed of QFP algorithm is much faster than that of joint SDR and D.C.iterative algorithm,which is consistent with the previous complexity analysis results.This is due to the fact that D.C.algorithm is embedded in the joint SDR and D.C.iterative algorithm,and the two-tiers loop causes the algorithm to converge slowly.As shown in this figure,when both algorithms reach the convergence state,their energy efficiency is very close,further verifying the superiority of the QFP algorithm.

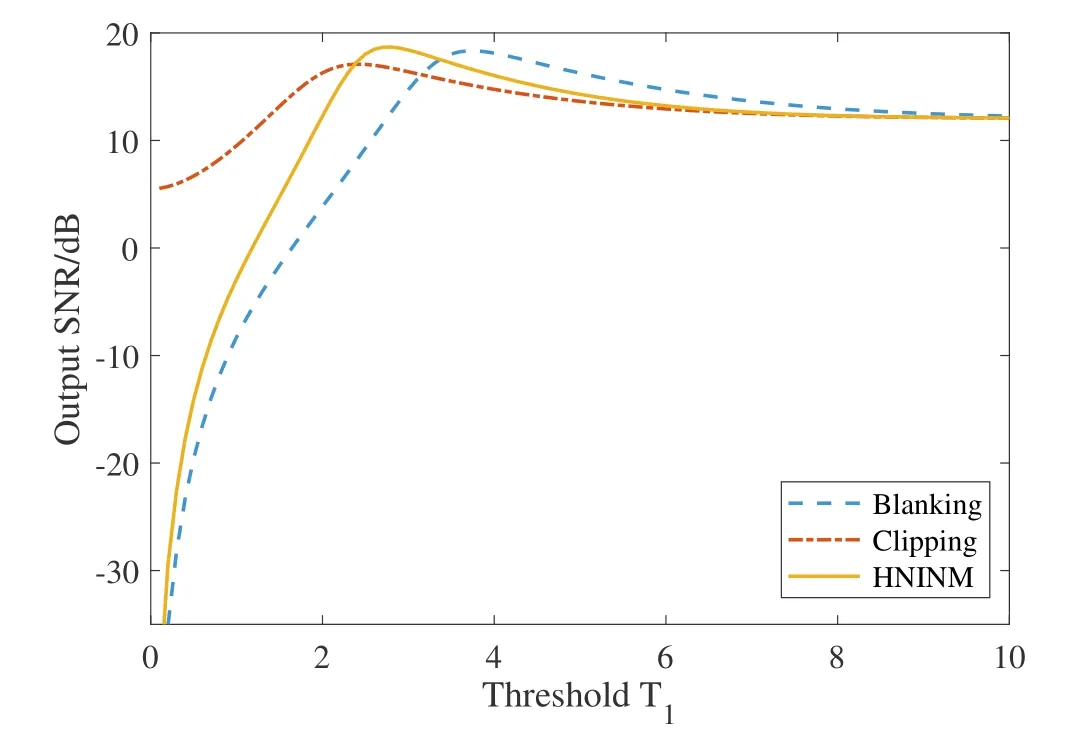
Figure5.Comparison of the output SNR when adopting different thresholds among different noise mitigation methods.

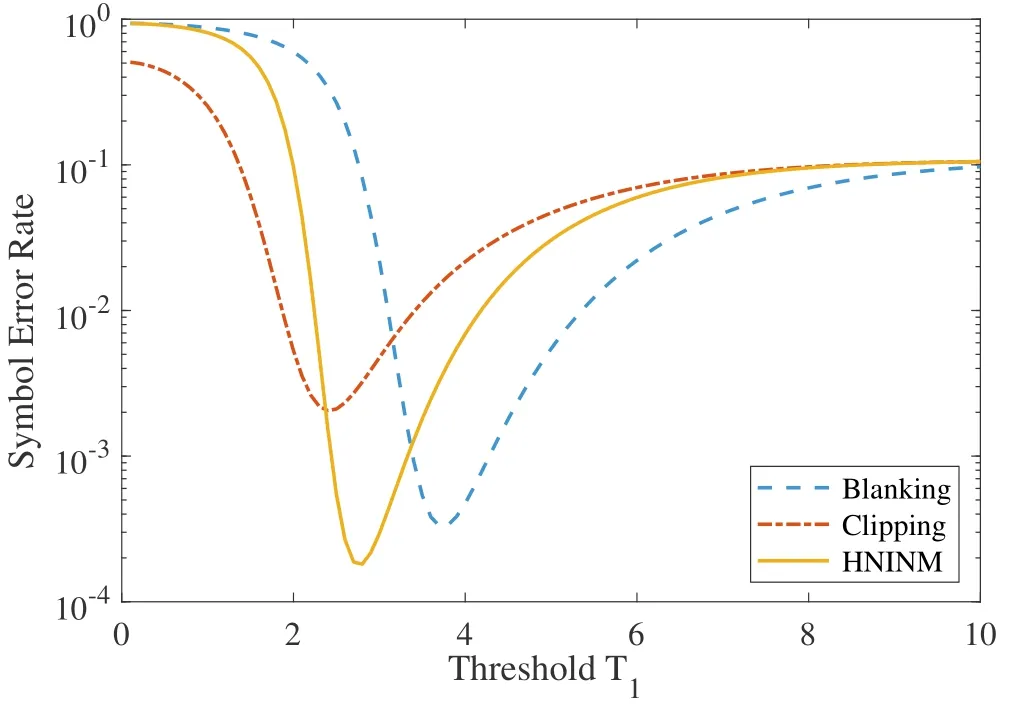
Figure6.Comparison of the SER when adopting different thresholds among different noise mitigation methods.

The proposed HNINM scheme can mitigate IN while retaining useful signals.For this purpose,it is imperative to select an appropriate thresholdT1for Eq.(29) to evaluate the performance of the HNINM scheme.The optimal threshold value cannot be expressed in a simple closed-form.Fortunately,numerical optimization does not introduce any difficulties and can easily be done by using standard numerical software tools.Figure5 and Figure6 analyze the influence of different thresholdsT1on the output SNR and SER.We notice that the selection of thresholdsT1is crucial to the output SNR and SER.The reason is that when the thresholdT1is too low,it will cause the amplitude of most useful OFDM signals to be zero,resulting in poor performance.Conversely,when the thresholdT1is too high,it is equivalent to not performing IN mitigation and causing a decrease in system performance.Simultaneously,three different nonlinear IN mitigation schemes are simulated in Figure5 and Figure6.Although the optimal threshold of different IN mitigation schemes is different,the proposed HNINM scheme can obtain the lowest SER at the optimal threshold,which further verifies the effectiveness of the proposed HNINM method.

VI.CONCLUSION

In this paper,we propose the MU-MISO-OFDM system framework,which is based on the joint transmitter and receiver design,to achieve efficient and reliable communication for the power-limited industrial wireless IN environment.At the transmitter,two precoding schemes were designed to maximize energy efficiency.To combat the non-convexity and fractional form,the joint SDR and D.C.iterative algorithm was designed after utilizing the Dinkelbach method to reconstruct the formulated problem into a two-tier alternating problem,which is a tractable convex optimization problem.To release the algorithm complexity,the QFP algorithm was designed by employing twotier quadratic transform and the optimal solution was solved by an iterative closed-form expression.At the receiver,the HNINM scheme was adopted to clipping or blanking the received signal to suppress the situation where the IN causes the SER to increase sharply.Simulation results showed that the performance of the proposed QFP algorithm was superior to the joint SDR and D.C.iterative algorithm.Furthermore,the HNINM scheme improved the reliability of the communication system.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China under Grant 62071472,and in part the Program for“Industrial IoT and Emergency Collaboration” Innovative Research Team in CUMT(No.2020ZY002).

APPENDIX

Proof of Rank-one

We prove that the optimal solution to theP3 is rankone.SinceP3 is convex and satisfies the Slater’s condition,the strong duality holds and the Karush-Kuhn-Tucker (KKT) conditions are the sufficient and necessary conditions for a primal-dual point to be optimal.The partial Lagrangian function of the optimization problemP3 is given by

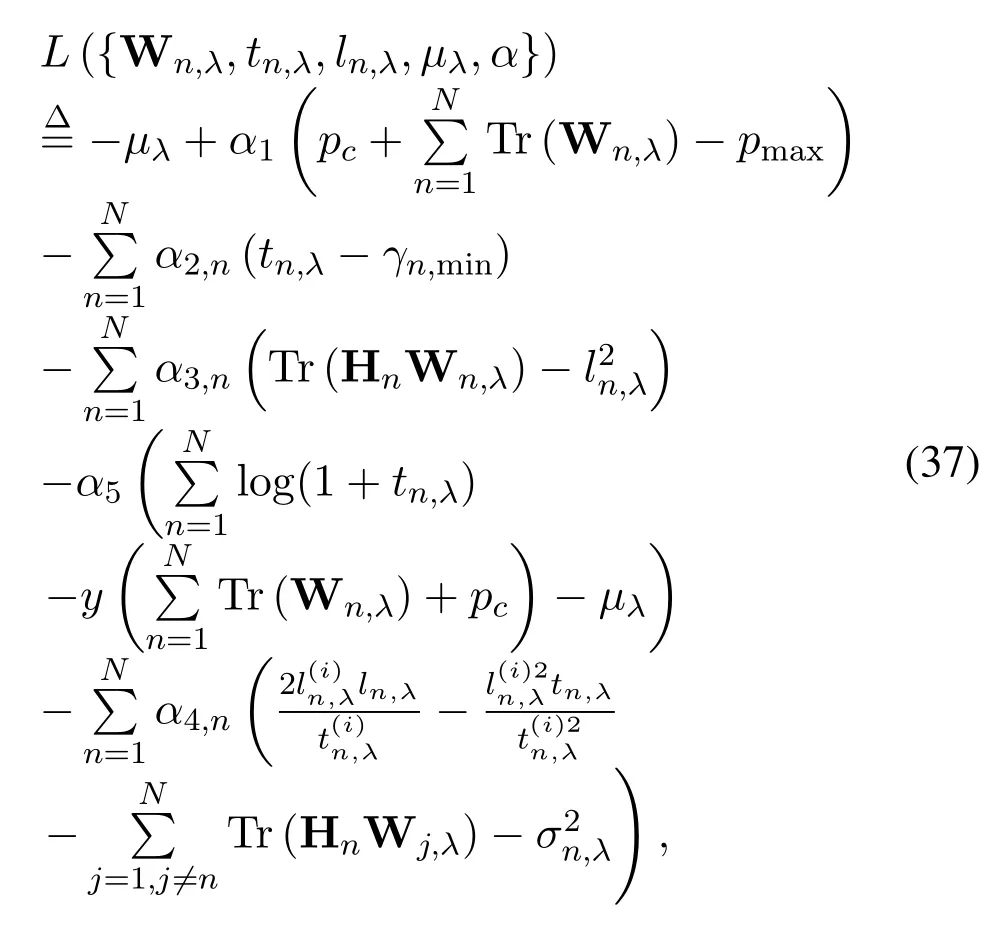
whereα={α1,α2,n,α3,n,α4,n,α5}is the Lagrangian dual variables.So the dual problem ofP3 is expressed as Eq.(38).

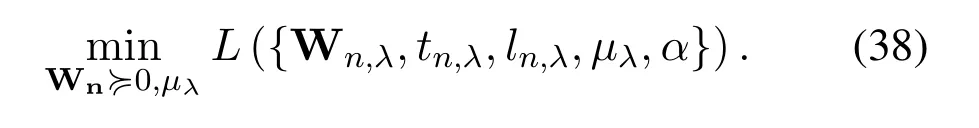
We bring Eq.(37) into Eq.(38),then it can be explicitly written as Eq.(39).

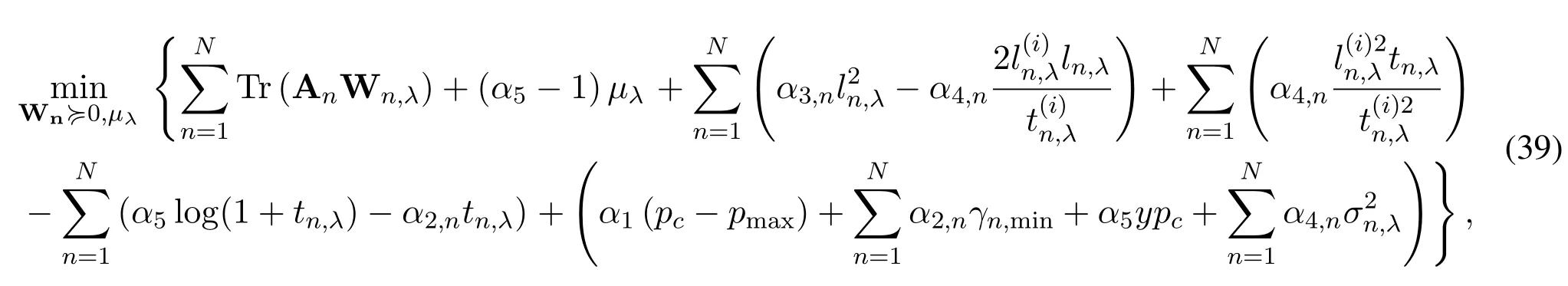
where

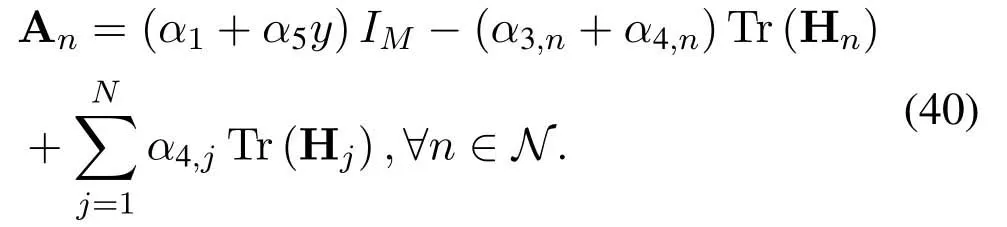
Using the first-order optimality conditions,we have

From Eq.(37)and Eq.(41),we haveα∗5=1,α∗2,n >0,α∗3,nandα∗4,nare both zero or greater than zero.

Obviously,for any givenn,W∗nλis the solution to the following problem

We prove that for both it is impossible for bothα∗3,nandα∗4,nto be zero for anynby contradiction.Let us define non-empty setsand B∗=respectively,we have

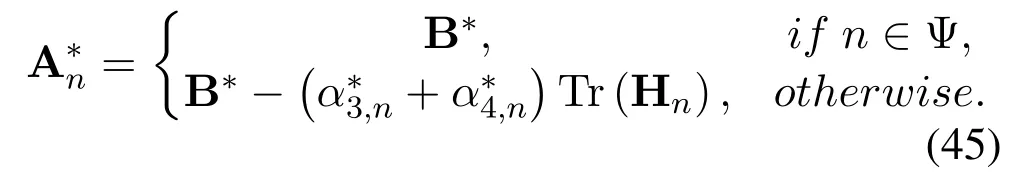
Since A∗n≽0 andit is easy to deduce B∗≽0.In the following,we prove that B∗≽0 by contradiction.We assume that the minimum eigenvalue of B∗is zero.There is at least one wn,λ /=0 that makes wHn,λB∗wn,λ=0 hold.According to Eq.(45),it follows that wHn,λA∗nwn,λ=n /∈Ψ.

Note that we haveα∗3,nandα∗4,nare both greater than zero.As a result,we obtain that|hnwn,λ|2≤0,n /∈Ψ.It thus follows that hnwn,λ=0,n /∈Ψ.

Therefore,we can infer

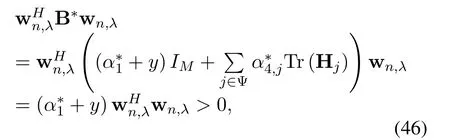
which contradicts the previously hypothetical wHn,λB∗wn,λ=0.Thus,we have B∗ ≻0,which is Rank(B∗)=M.It is easy to obtain Rank(A∗n)=Mfrom Eq.(45)ifn ∈Ψ.According to Eq.(44),we haveW∗n,λ=0 ifn ∈Ψ,which is obviously not the optimal solution.Therefore,it can be derived that Ψ/=∅.Eq.(45)thus reduces to

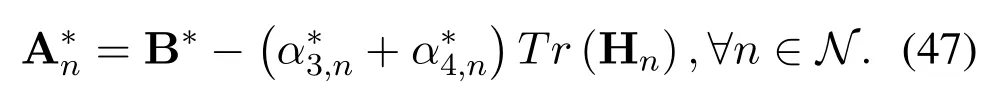
It is easy to deduce that Rank(A∗n)≥M −1.The optimal solution cannot be obtained when A∗nis of full rank.Therefore,it follows that Rank(A∗n)=M −1.On the basis of Eq.(44),the proof of Rank1 is thus completed.

Derivation of Output SNR

The OFDM signal with large number of subcarriers can be modeled as a complex Gaussian process with Rayleigh envelope distribution.Without loss of generality,the input OFDM signalxnpower is normalized asσ2x=1,which satisfies the Rayleigh distribution.Hence,the precoding signalsnpower obeys the Rayleigh distribution with parameterσ2s=which meansE

Similarly,the output signalynpower follows the Rayleigh distribution with parameterThus,joint probabilityP(D0,λ) andP(D1,λ) can be expressed as

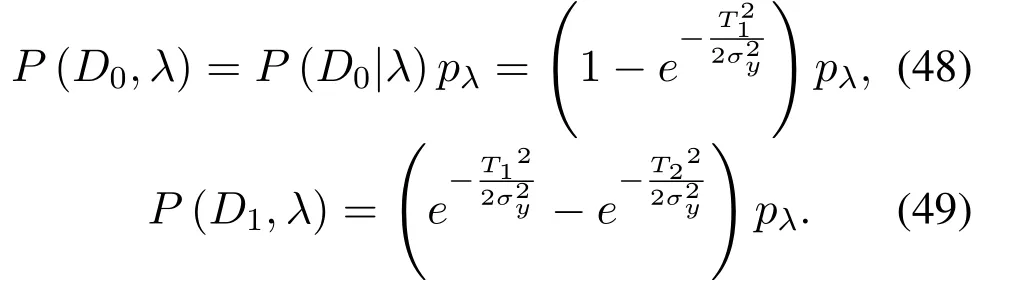
Next,we deriveandE[yns∗n].The total signal power at the output of hybrid nonlinear noise mitigation module can be written as

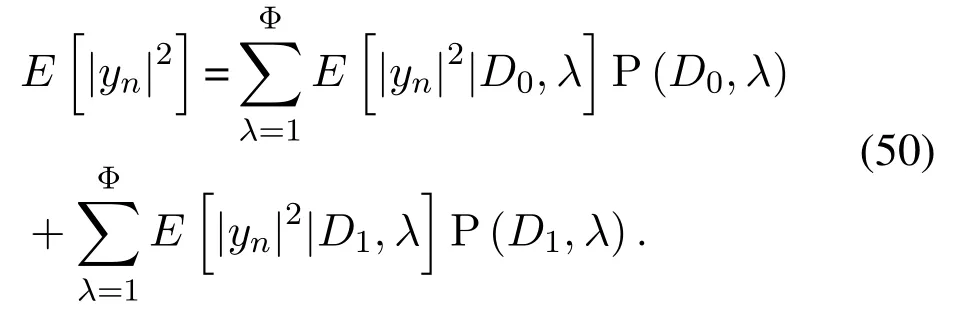
According to the work presented in [12],we can obtain the conditional PDFf(|yn||D0,λ) andf(|yn||D1,λ) by using Bayes theorem,respectively.As a result,conditional expectationEandEcan be expressed as

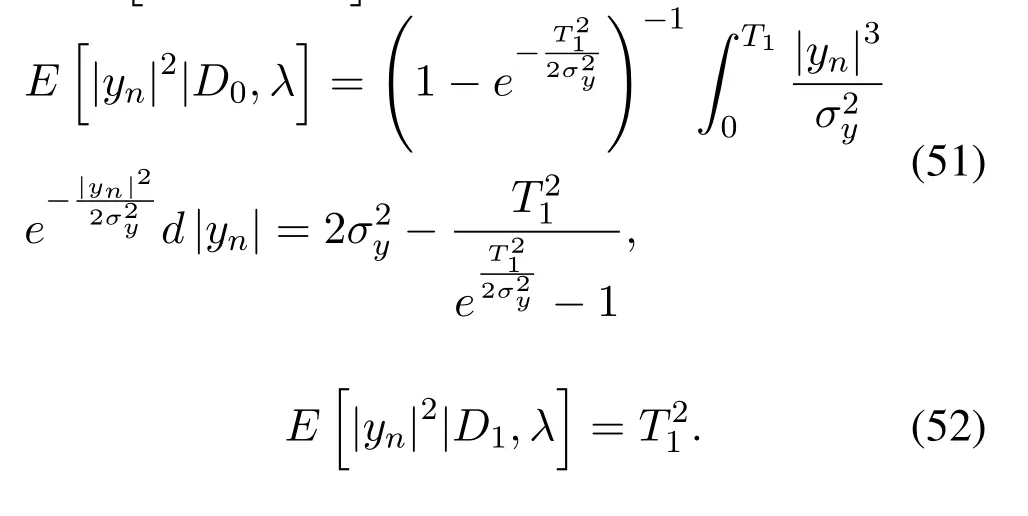
Substituting Eq.(48),Eq.(49),Eq.(51)and Eq.(52)into Eq.(50),we havei.e.Eq.(34).

From[11],E[yns∗n]is given by

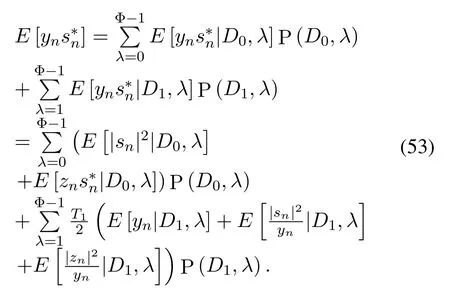
Similar to[12],we have Eq.(54).

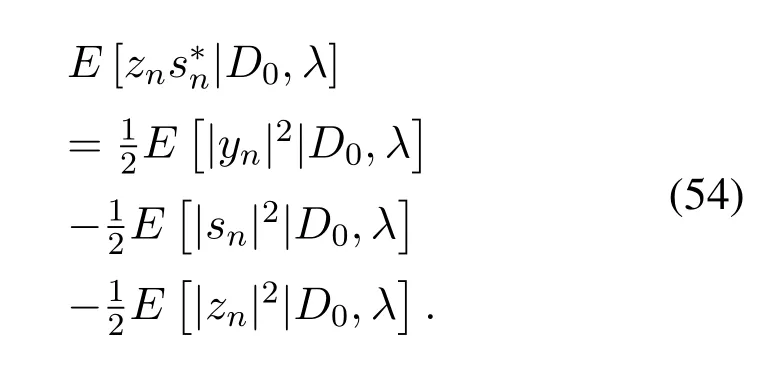
f(|sn||D0,λ) can be represented easily andcan be expressed as

where the second integral can be expressed analytically using the results presented by the work in[39].

The IN signalznpower obeys the Rayleigh distribution with parameterσ2z=σ2n,λ.We can obtain conditional PDFf(|zn||D0,λ).Thus,

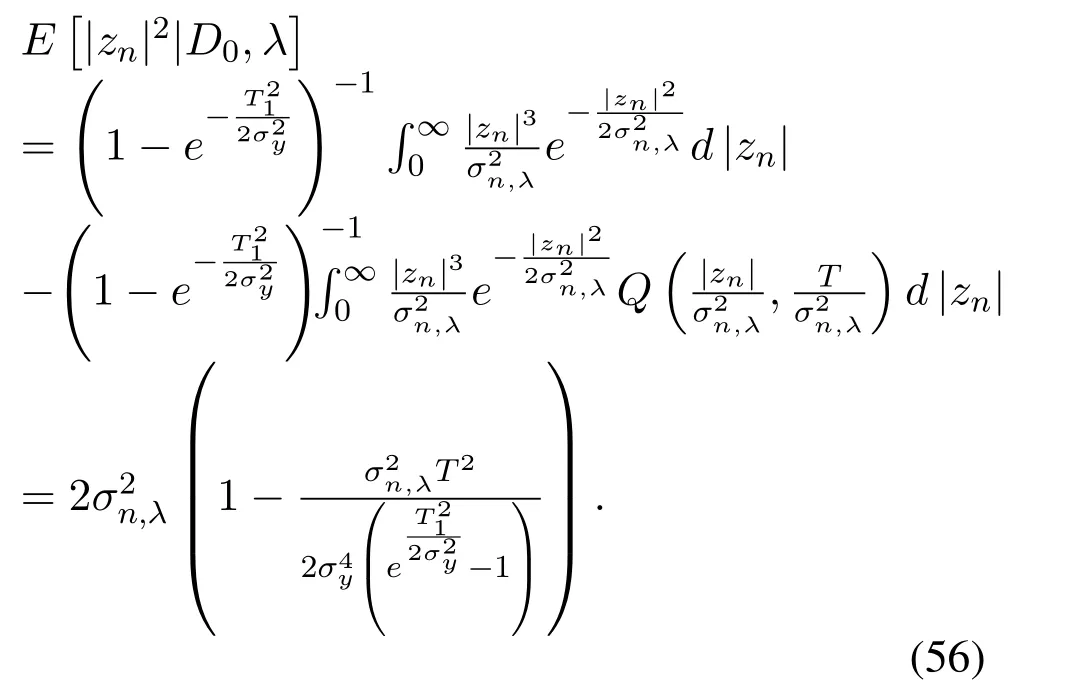
Substituting Eq.(51),Eq.(55),Eq.(56) into Eq.(54),we have

In order to facilitate the solution,we directly solveE[yns∗n|D1,λ]P(D1,λ) instead of solvingE[yns∗n|D1,λ]and deduce

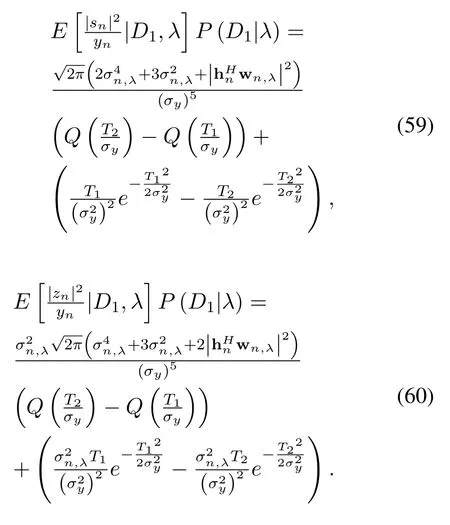
We bring the above formula into Eq.(53) to getE[yns∗n],i.e.Eq.(35).