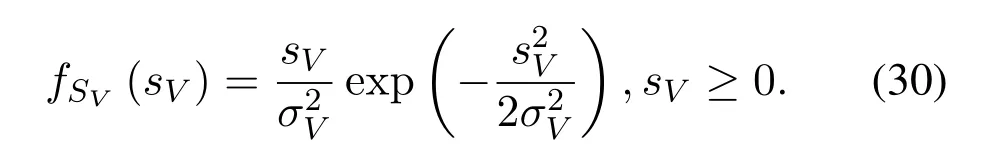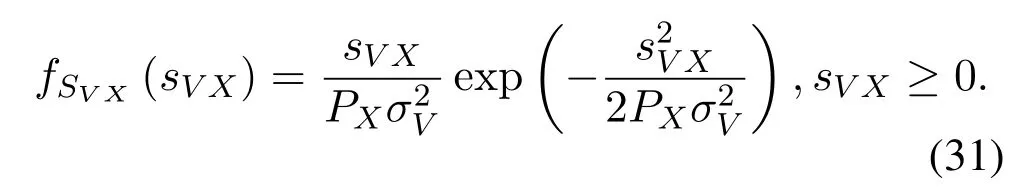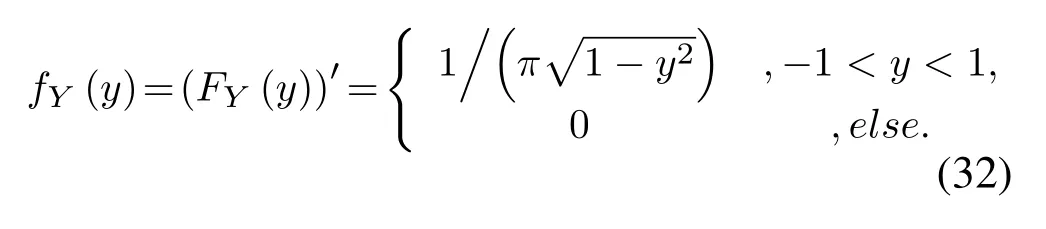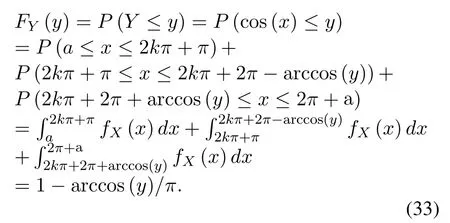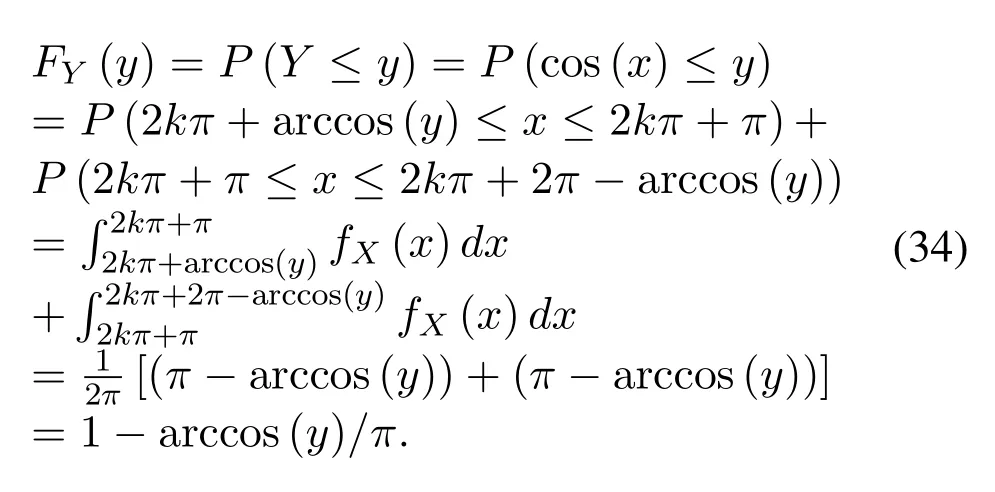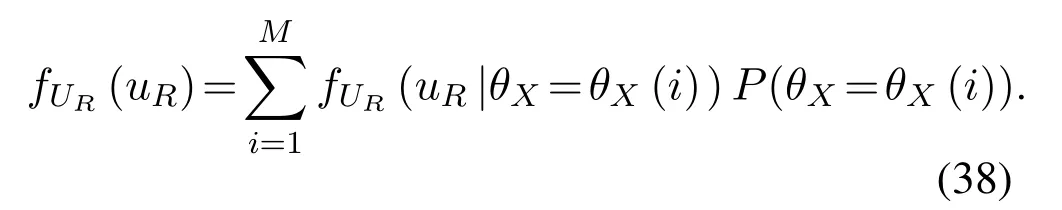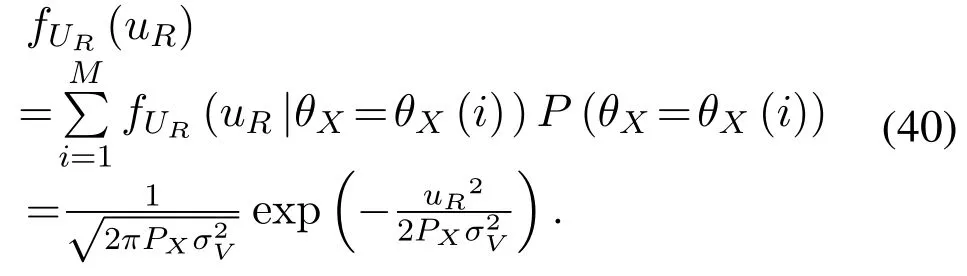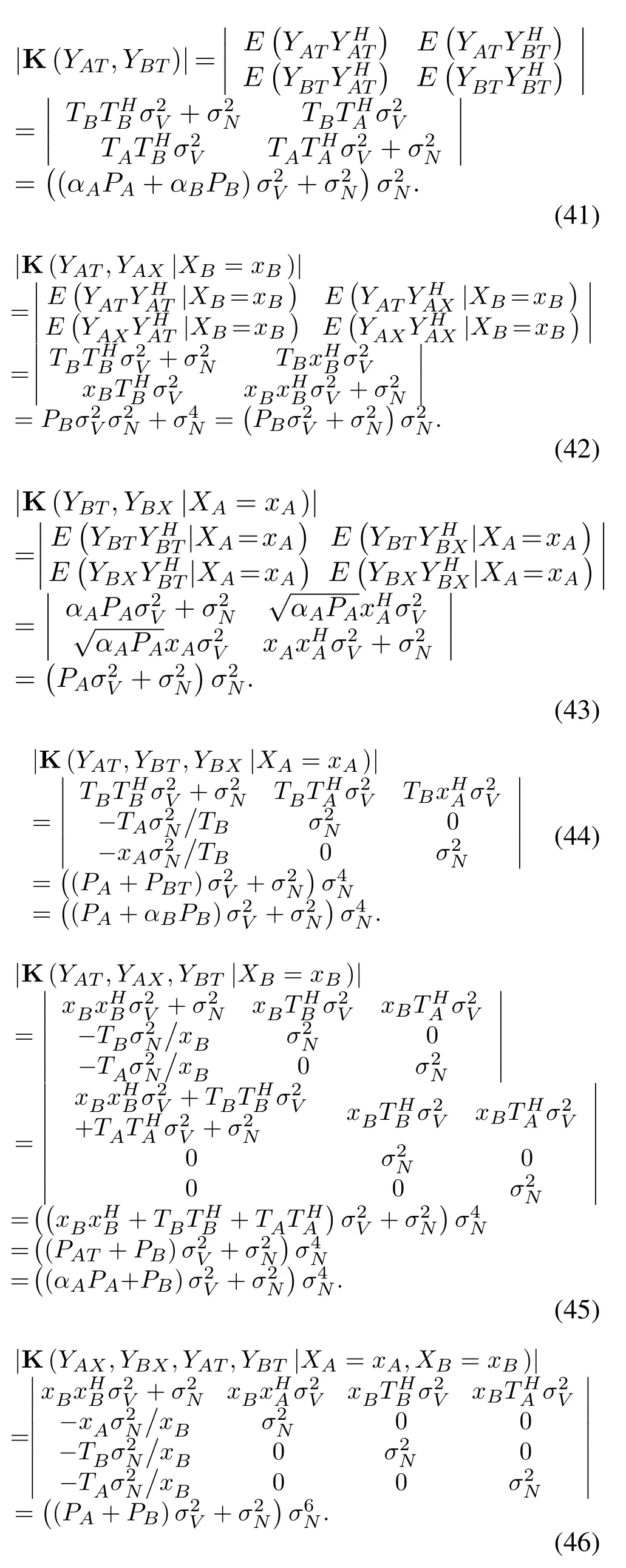Analysis and Application of Endogenous Wireless Security Principle for Key Generation

Xu Wang,Liang Jin,Yangming Lou,Xiaoming Xu

Information Engineering University,Zhengzhou 450001,China

Abstract:The open and broadcast nature of wireless channels leads to the inherent security problem of information leakage in wireless communication.We can utilize endogenous security functions to resolve this problem.The fundamental solution is channel-based mechanisms,like physical layer secret keys.Unfortunately,current investigations have not fully exploited the randomness of wireless channels,making secret key rates not high.Consequently,user data can be encrypted by reducing the data rate to match the secret key rate.Based on the analysis of the endogenous wireless security principle,we proposed that the channel-based endogenous secret key rate can nearly match the maximum data rate in the fast-fading environments.After that,we validated the proposition in an instantiation system with multiple phase shift keying(MPSK)inputs from the perspectives of both theoretical analysis and simulation experiments.The results indicate that it is possible to accomplish the onetime pad without decreasing the data rate via channelbased endogenous keys.Besides,we can realize highspeed endogenously secure transmission by introducing independent channels in the domains of frequency,space,or time.The conclusions derived provide a new idea for wireless security and promote the application of the endogenous security theory.

Keywords:endogenous wireless security;one-time pad;physical layer security;secret keys generation

I.INTRODUCTION

Based on the basic principle of philosophy,there is almost no natural or artificial system that solely has one function in the sense of logic[1].That is to say,for any system,there are accompanying functions besides the expected ones.However,at the beginning of system design,designers usually focus on realizing the expected functions whereas ignoring the side effects and accompanying functions they could bring into the system.This gives chances to malicious attackers.These security matters caused by the accompanying functions are called endogenous security problems.Specifically,wireless communication systems are designed to transmit user data as fast as possible via electromagnetic waves.However,the open and broadcast nature makes wireless systems have the serious accompanying function that the receivers within the radiation range of a transmitter could receive copies of user data[2,3].This accompanying function allows attackers to eavesdrop on the transmission between legitimate transceivers,causing the inherent problem of information leakage.

The fundamental solution to inherent problems should be endogenous mechanisms.That is because the internal cause is the root cause of the development of things,whereas external causes cannot work without internal causes independently.Unfortunately,current commercial wireless communication systems protect their security by plugging in encryption modules[4],whose designs are independent of the communication process.Besides,the development of security issues usually lags behind communication.Though encryption algorithms are constantly updating to enhance security,the external essence of passive defense systems established on security evolution strategy with patching inevitably leads to the curse of being continuously broken[5–8],just like the sword of Damocles hanging overhead.What makes it worse,in the upcoming Internet of Everything era [9,10],the overhead of the distribution and updates of secret keys will increase exponentially,leading to severe network congestion.This could be even worse in situations (like the network of unmanned aerial vehicles[11])whose adjacent nodes change frequently.These matters further constrain the application of encryption methods.Therefore,it is urgent to develop mechanisms that fully excavate the endogenous security functions of wireless communication to cope with inherent security problems.

Endogenous security is attracting great attention.One of the typical representatives is the quantum key distribution(QKD),which applies the quantum entanglement property to distribute secret keys in optical communication.For wireless communication,the endogenous security property comes from the positionbounded wireless channels.The channel-based physical layer secret keys provide an endogenous security scheme to solve information leakage in wireless communication [12,13].Concretely,the scattering,reflection,refraction,and diffraction effects experienced by electro-magnetic waves during transmission make wireless channels have the endogenous properties of uniqueness,reciprocity,time-variant,and randomness[14].Particularly,when legitimate transceivers undertake bi-directional transmission within a channelcoherent period,the channel state information in the received signals at both sides are strongly correlated,which makes the wireless channel a promising candidate of common randomness to generate secret keys.Armed with this discovery,the channel-based key distribution(CKD)[15–19]emerges as the times require.Because the channel information transfer process is embedded in wireless communication,the CKD is an endogenous security strategy.In the following paper,the channel-based physical layer secret keys are called endogenous secret keys.

Unfortunately,current investigations on CKD have not fully exploited the endogenous security functions in wireless communication.Based on the source-type model[15]and the secret key capacity[15,17],Zhang[20]calculated the closed-form expressions of the endogenous key rate from received pilot signals.Besides,researchers applied the reciprocal phase components of wireless channels[21,22],the channel impulse response (CIR) [23,24],and the received signal strength (RSS) [25–29]to generate secret keys.Recently,researchers are interested in applying the endogenous secret keys to the practical applications[28,30].However,these existing investigations utilized either received pilot signals or the power level of received data signals[30],which makes key rates quite low [31–34].The secrecy of data could be achieved by decreasing the data rate to match the secret key rate [35,36].Therefore,we investigate the ways to improve the endogenous keys generation by using the signals of pilots and data jointly.

In reality,during the wireless communication process,wireless channelVis transmitted along with the sourceX.Therefore,there are both channel state information and user data in the received signalY=V X+N.Consequently,there are both messages carried user data stream and security concerned secret keys stream in wireless communication.The sources of entropy inVandXare different,which are determined by the environments and humans,respectively,butVandXappear as an ensemble and are symmetrical in the expression of received signals.Therefore,similar methods can be applied to recoverVandX.Based on the above analysis,we propose that when the channel entropy is large enough,the endogenous secret keys can nearly match the maximum data rate,thus achieving the one-time pad without reducing the data rate.

This paper focuses on the problem of guaranteeing the secrecy of user data via the channel-based endogenous secret keys from the received signals of both pilots and data.Specifically,we investigate the fundamental laws about the rates of data and secret keys in wireless systems to validate the proposition.Firstly,information theory is utilized to analyze the endogenous security principle of wireless transmission qualitatively and distill the unexploited secrecy improvements,based on which we put forward the proposition.Secondly,we adopt the instantiation validation to verify the proposition.Specifically,in the wireless system with multiple phase shift keying (MPSK) inputs,we investigate the relationship between the secret key rate and the maximum data rate.Finally,conclusions are drawn based on the results from theoretical analysis and simulation experiments.

The main contributions of this paper are listed as follows:

1.New proposition:This paper proposed a new proposition that in a fast-fading environment,it is possible to make the channel-based endogenous secret key rate nearly match the maximum data rate.This proposition is validated in an instantiation system with MPSK inputs from the perspectives of both theoretical analysis and simulation experiments.

2.New viewpoint:This paper applied the endogenous security functions to solve inherent security problems.To be more specific,this paper provided a pilot-data joint viewpoint to generate endogenous secret keys from the received signals of both pilots and data.

Notation:Italic capital letterXdenotes the random variable whose realization is denoted by its lowercasex.The boldface capital letter X represents a random vector or matrix whose realization is denoted by its lowercasex.XHis the conjugate transpose ofX,XTis the transpose operation.The entropy ofXis denoted byH(X),the mutual information betweenXandYisI(X;Y).

II.SYSTEM MODEL

As shown in Figure1,legitimate transceivers Alice and Bob want to carry out real-time perfectly secure communication as fast as possible under the circumstance with a passive eavesdropper Eve,which can only passively eavesdrop on the communication but cannot send any interference signal.We assume that Alice and Bob are equipped with one antenna whereas there is no constraint on the antenna number of Eve.The legitimate channel between Alice and Bob is denoted byV.The eavesdropping channels between Alice(Bob)and Eve are denoted by GAE(GBE).

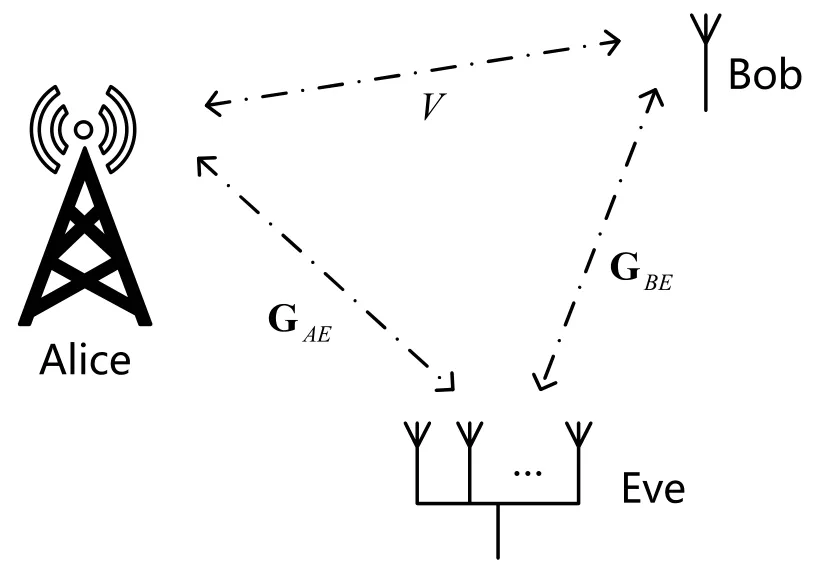
Figure1.System model.

For ease of understanding,we call the channel from Alice to Bob as the downlink wireless channel and uplink channel in the reverse direction.We assume that Eve has infinite computation capacity and can get all the transmission-related information,like the modulation scheme,frame structure,keys generation method,and the data encryption method.Alice and Bob encrypt user data by the keys from wireless channels.The data encryption and decryption methods utilized by Alice and Bob are the lightweight bit-by-bit XOR operations.Eve utilizes the same keys generation method as Alice and Bob to generate keys from the estimated eavesdropping channels.After that,Eve applies the extracted keys to decrypt the encrypted user data.As we investigate the data rate and the key rate from the perspective of information theory,no keys generation method is specified.

This paper considers the case when Eve can recover the eavesdropping channels and the encrypted user data.If the distances from Eve to Alice or Bob are much smaller than a half wavelength,GAE(or GBE)andVare strongly correlated.Then,Eve can recover the channel-based keys shared between Alice and Bob.After that,Eve can recover the user data of Alice and Bob,which are denoted asSAandSB,respectively.

In order to guarantee the secrecy of user data,we assume that GAEand GBEare independent ofV.The independence of wireless channels is easy to satisfy.Theoretically speaking,in the uniform scattering environment,wireless channels are independent of each other if the distance between two receivers is larger than a half wavelength [14,37,38].Furthermore,the practical test of wireless channels in Manhattan showed that the wireless channels were largely uncorrelated even at antenna separations as small as two wavelengths[39].

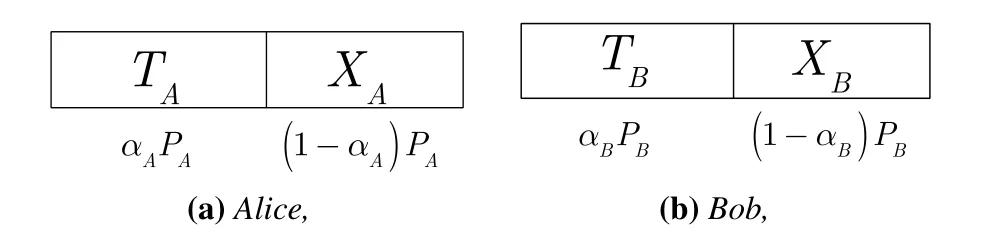
Figure2.The frame structure of Alice and Bob.

We assume that the wireless channel is blockfaded and that Alice and Bob only carry out one bidirectional transmission during the channel-coherent period with the frame structure given in Figure2.The pilot and the encrypted user data symbol of Alice (Bob) are denoted byTA,XA(TB,XB).The channel-based endogenous secret keys between Alice and Bob are denoted byK=(KA,KB),whereKAandKBare the keys utilized to encryptSAandSB,respectively.Then,we haveXA=XOR(KA,SA)andXB=XOR(KB,SB).We assume that the total power isPand that the power of Alice,denoted byPA,isβP,whereβ ∈[0,1].The power of Bob,denoted byPB,is (1−β)P.Furthermore,Alice (Bob) allocatesαAPA(αBPB) to send the pilot,whereαA,αB ∈[0,1].The power that Alice and Bob can allocate to pilots and user data symbols arePAT=αAPA,PAX=(1−αA)PA,PBT=αBPB,PBX=(1−αB)PB,respectively.

Figure3 shows one bi-directional communication process taking place within the channel-coherent period.Besides,we assume that there are additive noises in the system.Specifically,when Bob transmitsTBandXB,Alice receivesYAT=V TB+NATandYAX=V XB+NAXwhile Eve receives YET0=GBETB+ NET0and YEX0=GBEXB+ NEX0.Similarly,when Alice transmitsTAandXA,Bob receivesYBT=V TA+NBTandYBX=V XA+NBXwhile Eve gets YET1=GAETA+NET1and YEX1=GAEXA+NEX1.NAT,NAX,NBT,NBX,NET0,NEX0,NET1,and NEX1are the additive noises at corresponding receivers.

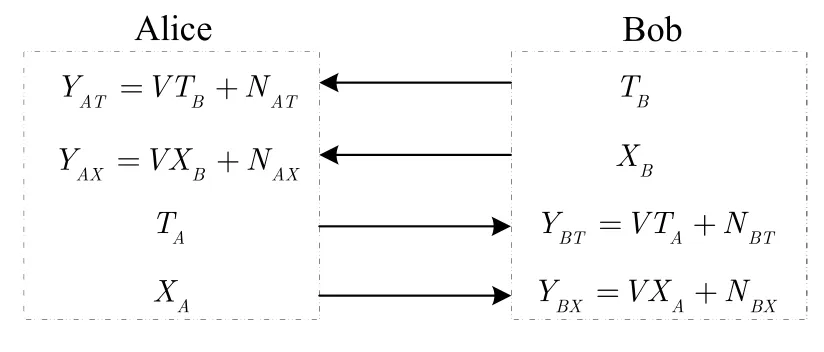
Figure3.Communication process.

III.ENDOGENOUS SECURITY PRINCIPLE AND PROPOSITION

This section proposes an information theoretical analysis framework with the observations from the communication process to distill the hidden security potentials and investigate the relationship between the rates of user data and secret keys,based on which we put forward a proposition.In comparison to the wireless communication process,we explain the physical meaning of each component.

We first introduce the random sources Alice and Bob can utilize to generate secret keys.XAandXBare the variants transmitted by Alice and Bob,respectively.According to Figure3,after one interaction of both pilot and user data symbols,variants known or received by Alice and Bob areXA,YAX,YATandXB,YBX,YBT,respectively.

Before introducing the main results,the secrecy constraints on the common randomness are analyzed.Specifically,we consider the case when Eve can recover the encrypted user data (XAandXB) and the eavesdropping channels (GAEand GBE) accurately.The boundary value of the common randomness between legitimate transceivers is deduced as

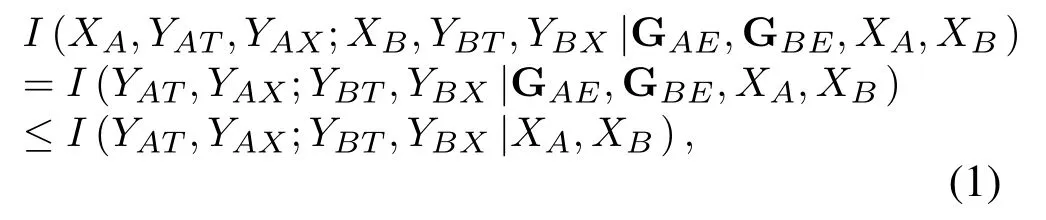
where the equal sign is achieved when the legitimate channel is independent of the eavesdropping channels.That is to say,whenVis independent of GAEand GBE,Eve cannot get the common randomness shared between Alice and Bob.

When Alice and Bob utilize the channel-based secret keys to encrypt the user data,if the secret key rate matches the user data rate,information-theoretic perfect secrecy can be achieved[35,36].At this time,Eve can recover neither the user data nor the secret keys with the eavesdropping channel state information and the encrypted user data.This paper focuses on the secrecy of user data via the channel-based endogenous secret keys from the received signals of both pilots and data.Therefore,we investigate the transmission of data and keys between Alice and Bob without Eve.

As the channel inputs are dependent on user data,which are independent of the wireless channel,XA,XB,andVare independent of each other.Hence,the overall information quantity[40]shared between legitimate transceivers over one bi-directional transmission is

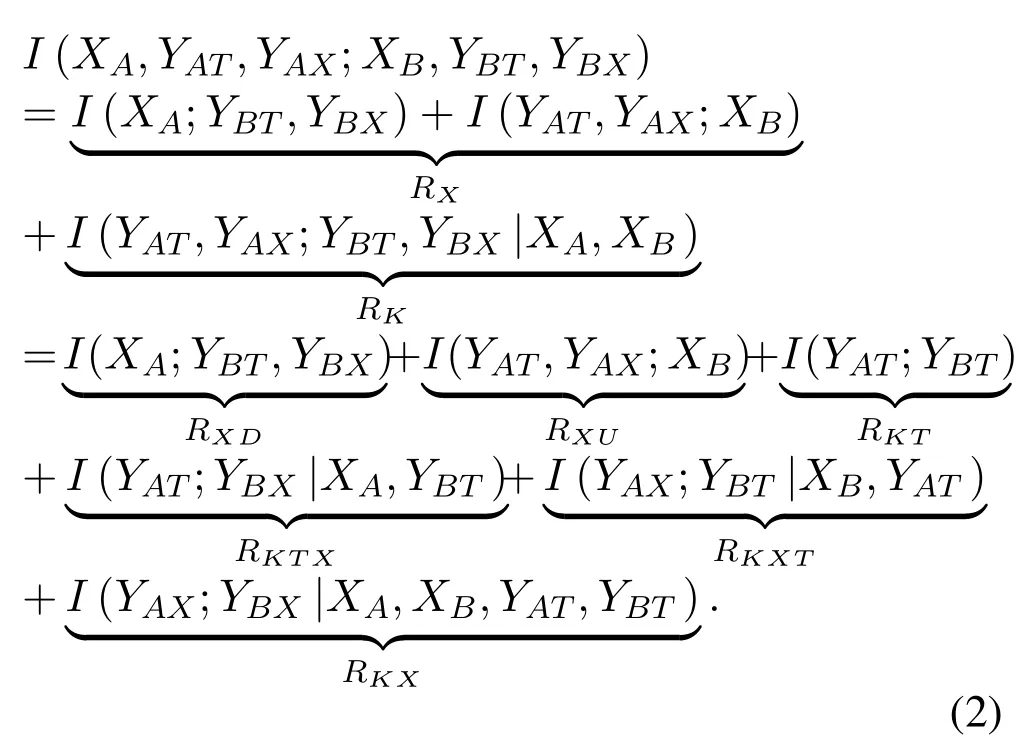
The first two elements describe the recovery ofXA,XB.Therefore,the sum of them,denoted byRX,is the achievable data rate.The sum of the last four elements,denoted byRK,is the amount of information shared between legitimate transceivers after deducting the randomness ofXAandXB.The legitimate channel determinesRKfor the reciprocity and randomness properties of wireless channels.Meanwhile,it should be noted that the common randomness of the last four elements comes from the legitimate channel,which is independent of eavesdropping channels for the uniqueness property of wireless channels.Hence,RKis the achievable secret key rate that Alice and Bob can extract from the communication process.For simplicity and without ambiguity,the achievable rates of data and secret keys are called data rate and secret key rate,respectively.

Precisely,the data rateRXconsists of the downlink data rateRXDand uplink rateRXU.The secret key rateRKconsists of the secret keys generated from the power of both pilots and user data.To be more specific,RKTis the key rate generated from the uplink and downlink pilot power,which is what the traditional physical layer secret keys investigate.RKTXis the key rate generated with the power of uplink pilot and downlink user data after deducting the keys from pilot power.LikeRKTX,RKXTis the key rate generated with the power of uplink user data and downlink pilot after deducting the keys from pilot power.RateRKXis the rate of keys generated with uplink and downlink user data power after deducting the keys generated inRKTXandRKXT[40].

The following conclusions can be inferred from(2).

1.Generalized communication.When transmitting the pilots and user data from a source to a destination,there are information streams of user data and wireless channels.Furthermore,channel state information is transmitted not only in the pilot transmission process but also in the data transmission process.Hence,the wireless transmission process is a kind of broad-sense communication.

2.Secret key improvements.According to the expressions ofRKT,RKTX,RKXT,andRKX,secret keys can be generated from the power of both pilots and user data.To be more specific,RKTX,RKXT,andRKXare the secret key improvements ignored by the traditional investigations on the pilot-based secret keys generation.

3.Automatic matching.In specific scenarios,the statistical characteristics of channelVand noiseNare determined.For a given power allocation scheme,when the total power of the system increases,the power of pilots and user data increases as well,decreasing the distortion effects caused by additive noises in (YAT,YBT,YAX,YBX).As a result,the recovery ability for channel state information and user data can be improved simultaneously.It indicates that the changing trends of the data rate and secret key rate are the same,which increases the possibility of automatic matching for these two rates.

4.Wide application scales.As the rates of user data and secret keys are extracted from the received signals,which happens in the signal level and has no constraints on the types of systems or mechanisms.The endogenous secret keys can be utilized to encrypt any kind of wireless communication.Nevertheless,this model is not applicable without limits.From (2),we can infer that both the rates of user data and secret keys are constrained by their entropy and background noises.The environment determines the background noises.Therefore,one of the constraints to ensureRKandRXmatch each other is that the entropy of wireless channels should be comparable to data,which corresponds to the fast-fading assumption.Anyway,the model proposed and the results derived have a wide range of applications.

In summary,the bi-directional transmission of pilots and user data is a generalized communication process that includes the usually neglected increments of channel state information.Besides,the source and channel appear as an ensemble and are symmetric in the received signalY=V X+N.Moreover,the background noises have similar distorting effects on the transmission of user data and pilots,making them have the same varying trends.Therefore,it is possible to make the endogenous secret key rate match the maximum data rate when wireless channels have enough entropy.Hence,it is reasonable to raise the following proposition.

Proposition 1.In a fast-fading environment,it is possible to make the channel-based endogenous secret key rate nearly match the maximum data rate.

Though it is hard to derive a closed-form expression to describe the relationship between the rates of data and secret keys accurately,the qualitative analysis of (2) indicates that wireless communication has the endogenous security property.The theory proposed can guide the design of endogenous security systems or evaluate the endogenous wireless security performance of a system.It provides a new direction to promote the practical applications of endogenous wireless security via channel-based secret keys.

IV.INSTANTIATION VALIDATION FOR PROPOSITION

Qualitative analysis in Section III shows that wireless communication has the potential to achieve endogenous security and points out the proposition that it is possible to make endogenous secret key rate match the maximum data rate.This section further demonstrates the proposition through instantiation validation,providing references to the endogenous security analysis in other scenarios.

To be more specific,this section investigates the relationship between the maximum data rate and the endogenous secret key rate.Therefore,we organize this section as follows.First,we make a theoretical preparation by listing the theorems and the entropy of observed variables.Second,we apply the upper bound analysis method to investigate the changing trends of the data rate,based on which we derive the optimal power allocation ratio for data transmission.Third,we derive the closed-form expression for the secret key rate.

4.1 Theoretical Preparation

According to the theoretical analysis of wireless channels in the uniform scattering environments [37,38]and the practical measurement of wireless channels in Manhattan,it is reasonable to utilize Gaussian variables to model wireless channels within the allowable range of measurement errors[39].Therefore,we assume that the wireless channels follow zero-mean complex Gaussian distribution and that user data are modulated by MPSK.Specifically,VandNfollows CN(0,σ2V)and CN(0,σ2N),respectively.Because the pilots are open and contain no information,pilots are only constrained with power.We introduce the following theorems to facilitate understanding.

Theorem 1.(The entropy of complex Gaussian random vector) WhenX=(X1,X2,···Xn)T is a complex Gaussian vector with mean vectorµand covariance matrixK=E((X−µ)(X−µ)H),then its entropy is H(X)=log2(πe)n|K|.(The proof is given in Appendix A).

Theorem 2.When V and N are complex Gaussian random variables,if X is modulated with finite MPSK symbols,the variable Y=V X+N is also a complex Gaussian random variable.(The proof is given in Appendix B).

For clarity and ease of understanding,we calculate the entropy of the variables mentioned in the instantiation system based on Theorem 1.Please refer to Appendix C for detailed derivations.

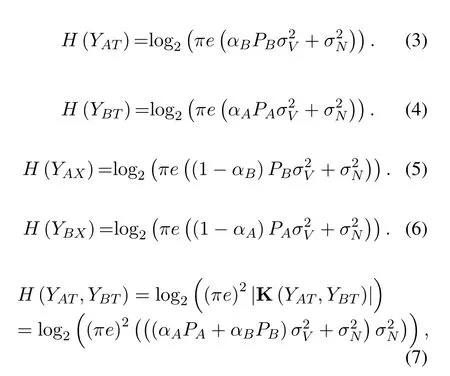
|K(YAT,YBT)|is calculated by(41)in Appendix C.

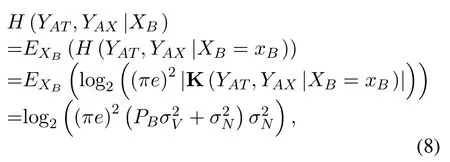
|K(YAT,YAX|XB=xB)|is calculated by (42) in Appendix C.

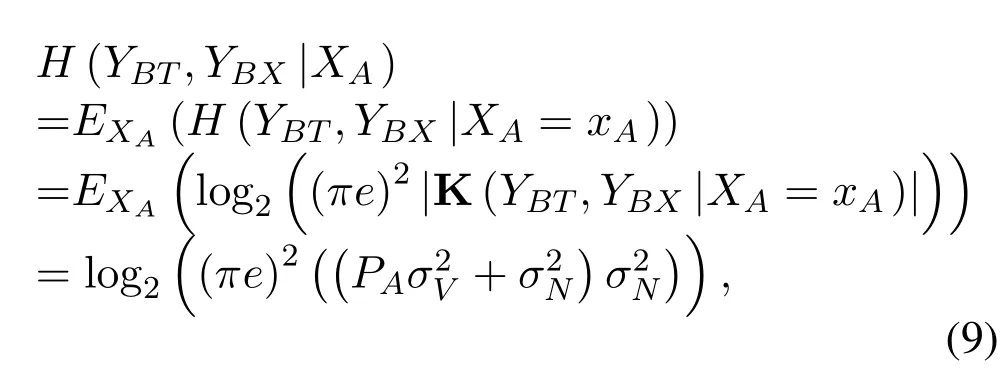
|K(YBT,YBX|XA=xA)|is calculated by (43) in Appendix C.

|K(YAT,YBT,YBX|XA=xA)|is calculated by(44)in Appendix C.

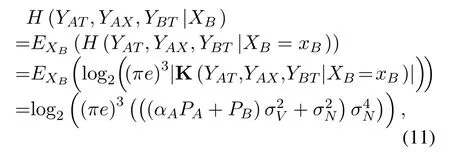
|K(YAT,YAX,YBT |XB=xB)|is calculated by(45)in Appendix C.

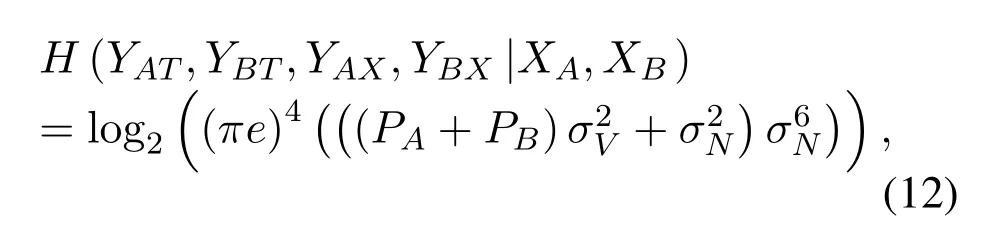
|K(YAT,YBT,YAX,YBX|XA=xA,XB=xB)|is derived by(46)in Appendix C.

4.2 Data Rate

When it comes to communication,how to achieve high rates is what comes first.Therefore,this part investigates the data rate and its affecting factors to determine the optimal power allocation scheme.It can be inferred from(2)that the data rate is the sum ofRXUandRXD,but its closed-form solution is very hard to derive.Hence,we adopt the upper bound of the data rate to investigate its varying trends.

4.2.1 The upper bound of data rate

As the analysis process is the same forRXUandRXD,without losing generality,this section takesRXDas an example to analyze the varying trends of data rate.

ThoughYBX(Theorem 2) andYBTare complex Gaussian random variables,they are not joint Gaussian distribution.That is becauseYBXis not a Gaussian random variable whenYBTis given.Therefore,Theorem 1 could not be utilized directly.However,whenXA=xA,(YBX,YBT|XA=xA)follows joint complex Gaussian distribution.Then the downlink data rate satisfies

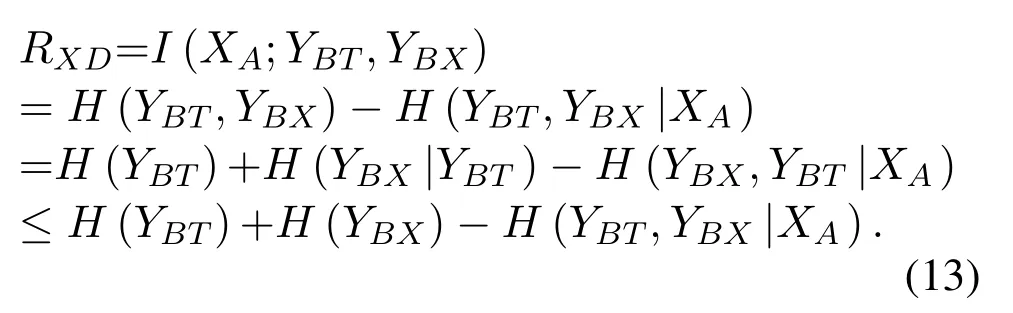
According to(4),(6),and(9),we can get

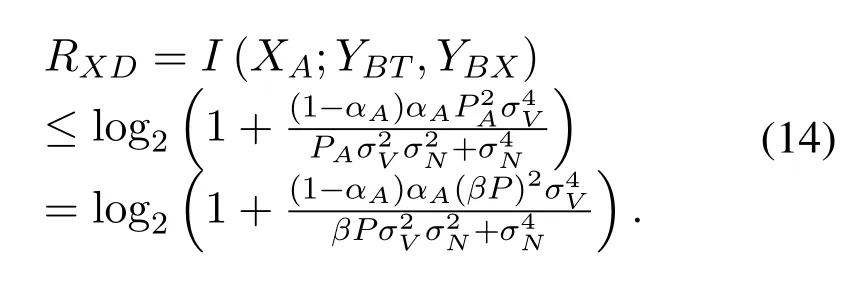
Similarly,the uplink data rate satisfies

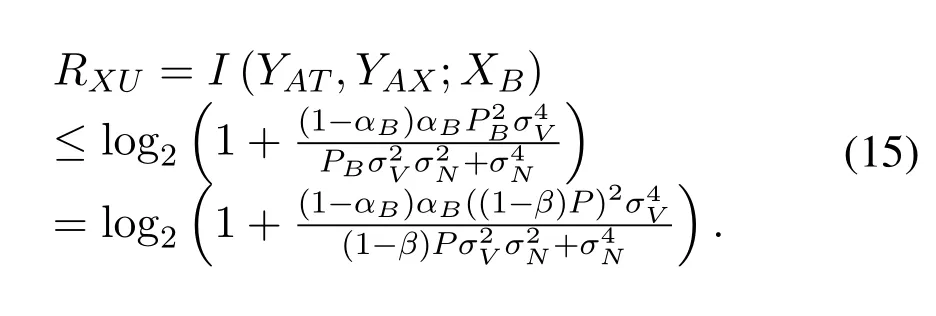
Consequently,the overall data rate satisfies

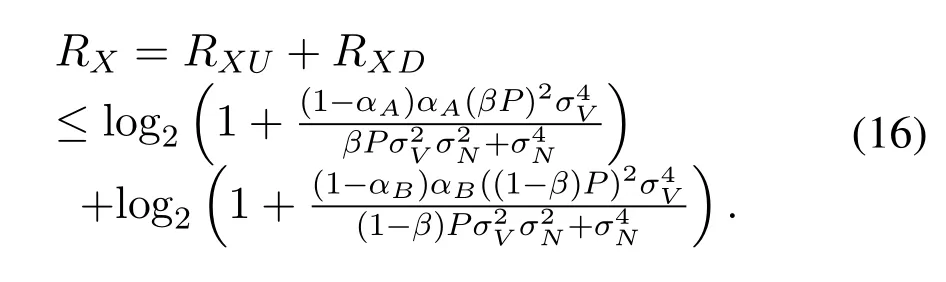
Though inequation (16) cannot describeRXaccurately,it can be used to investigate the varying trends and influencing factors ofRX.Specifically,inequation (16) shows that the upper bound of data rate is affected by the total powerP,the variance of channelsσ2V,the variance of noisesσ2N,the power allocation ratio of these two legitimate transceiversβ,and the pilot power ratioαA(αB).In a practical system,the variances of channel and noise are determined by the environment.The controllable factors includeP,β,αA,andαB.

4.2.2 Effects of power and power allocation scheme

In this part,we first study the effects of total powerP.Then,we investigate the optimal power allocation scheme for a givenP.We set the overall data rate as a function

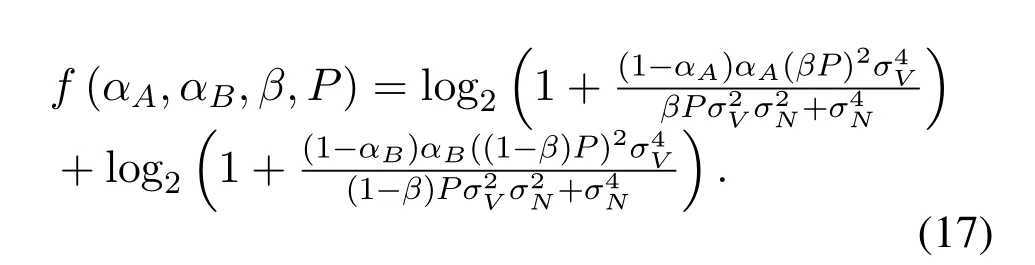
For the given(αA,αB,β),we take the partial derivative offtoPto investigate the effects of total powerPon the overall secret key rateRX.

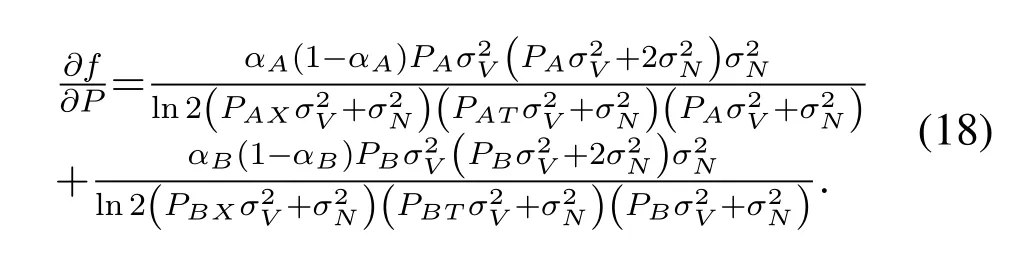
As∂f/∂P ≥0 is always true,whenαA,αB,andβare given,f(αA,αB,β,P)increases withP,i.e.,RXincreases withP.This corresponds to Conclusion 3 in Section III.Then we turn to the investigation on the optimal power allocation scheme for a givenP.Since

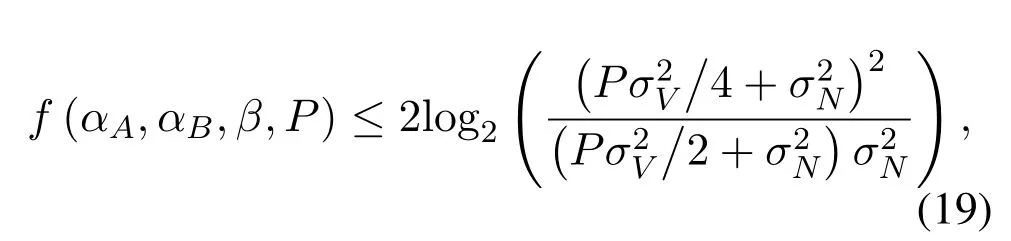
is true for all(αA,αB,β),the equal sign is achievable if and only ifαA=αB=β=0.5.Therefore,the optimal power allocation satisfiesαA=αB=β=0.5 for a givenP.

4.3 Secret Key Rate

This section investigates the elements and interfering factors of endogenous secret key rates.Firstly,we investigate the secret key rateRKTextracted from the pilot power.Secondly,we investigate secret key rate improvements (RKTX,RKXT,RKX) from the user data power.

4.3.1 Secret key rate from pilot power

Traditionally,physical layer secret keys are generated from received signalsYATandYBT.There is no randomness in pilots.Therefore,the common randomness ofYATandYBTcomes from the wireless channel.Given the assumption of wireless channels and additive noises,we can infer thatYATandYBTfollow complex Gaussian distribution.According to(3),(4),and(7),we can calculate the secret key rate from pilot power by

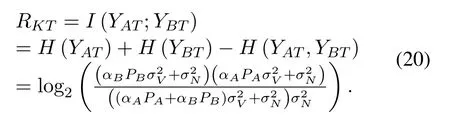
4.3.2 Secret key rates from user data power

After analyzing the secret keys extracted from pilot power,we now turn to the secret keys from user data power.According to (2),the hidden secret key rates from the transmitted user data consist of ratesRKTX,RKXT,andRKX,which are calculated in order.First,we calculateRKTXby

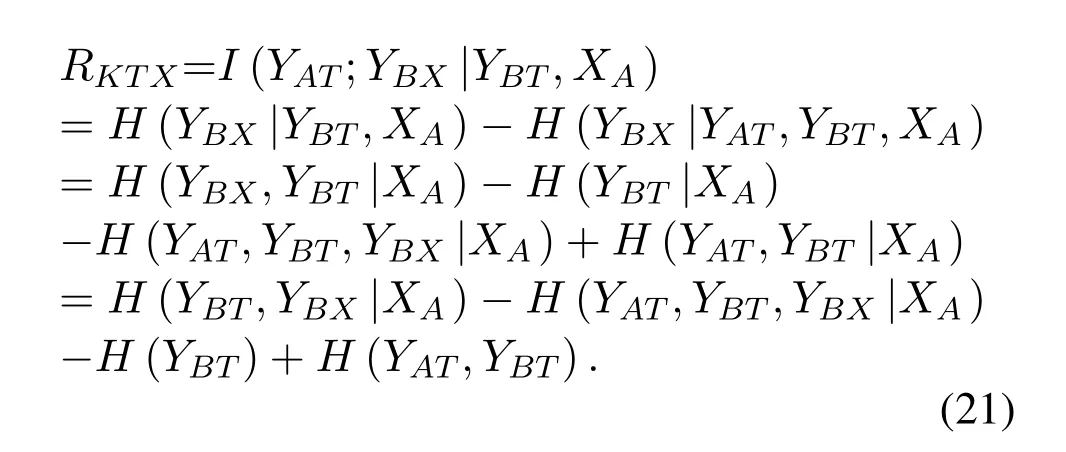
According to(4),(7),(9),and(10),we get

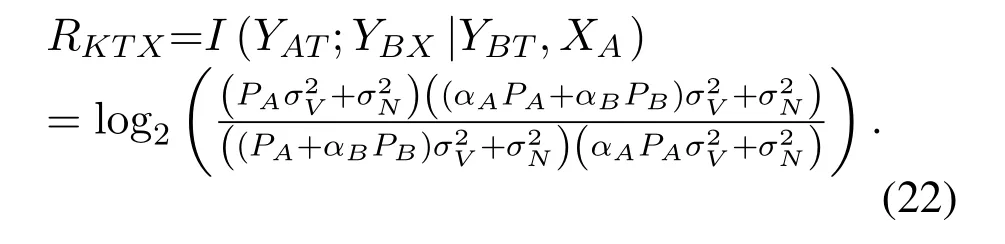
Similarly,according to (3),(7),(8),and (11),we have

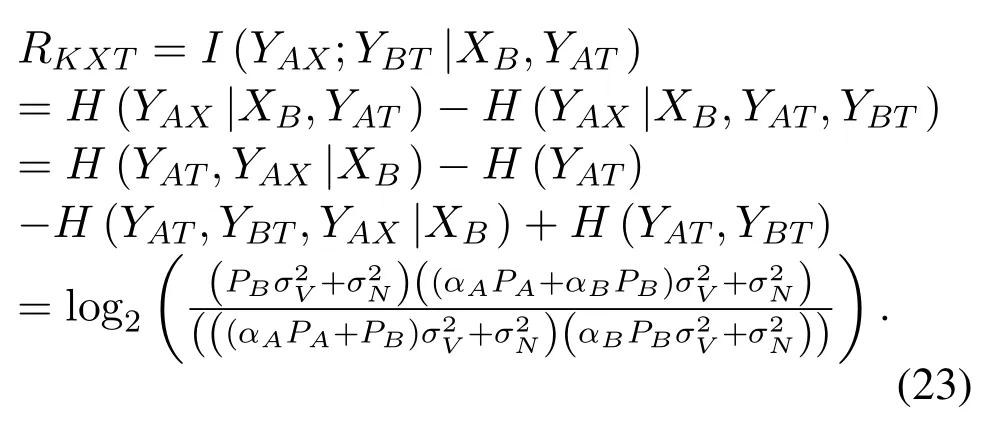
Next,we turn to the derivation ofRKX.

According to(7),(10),(11),and(12),we getRKXas

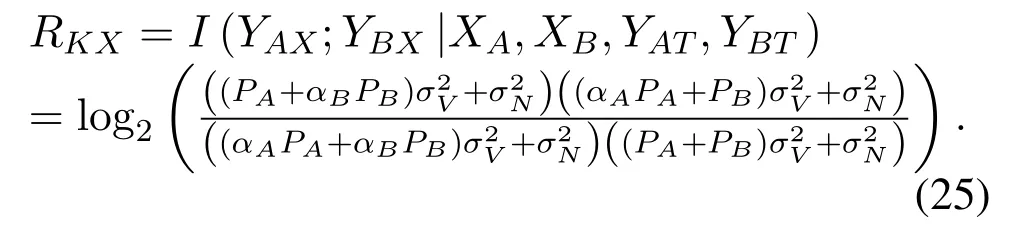
Summing up(20),(22),(23),and(25),we can calculate the overall endogenous secret key rateRKas

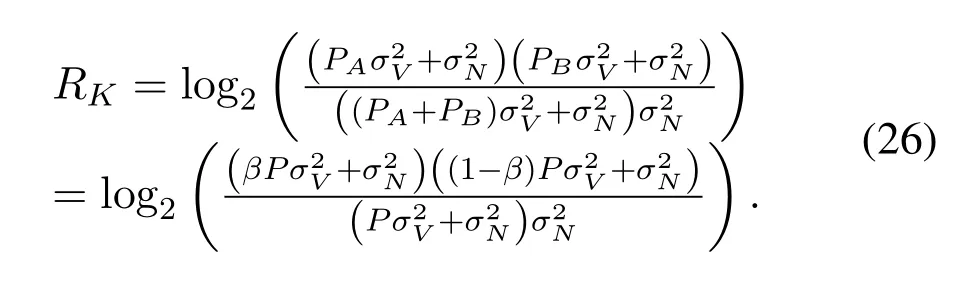
From(26),we learn that the endogenous secret key rate is affected by the overall power,the power allocation scheme,the variance of wireless channels,and the variance of additive noises.The power ratio that pilots take does not change the overall endogenous secret key rate.That is because after deducting the randomness of MPSK inputs,the transmission ofXAandXBhas effects on wireless channels with their power,which makesXAandXBequivalent to pilots.

Besides,we can infer from(26)that both the power of pilots and user data can extract secret keys with nonnegative rates.This validates Conclusion 2 in Section III.With the combination of (16) and (26),we learn that the rates of data and secret keys increase with the overall power.This corresponds to Conclusion 3 in Section III.Hence,wireless communication systems have the potential to make the endogenous secret key rate match the maximum data rate,thus achieving perfect secrecy.

V.SIMULATION

Based on the theoretical analysis of the instantiation system in Section IV,we carry out simulation experiments to validate the proposition.Firstly,we take simulations to determine the optimal power allocation schemes and validate the optimal power allocation scheme derived from the upper bound analysis.Then,we undertake simulations to exhibit the relationship between the maximum data rate and the secret key rate.

5.1 Effects of Power Allocation on the Rates of Data and Secret Keys

In the power-constrained communication systems,one of the key questions is determining the optimal power allocation scheme to maximize the data rate.Therefore,this section takes Monte Carlo simulations to exhibit the effects of power allocation on data rate as well as the secret key rate and validate the results drawn from the upper bound analysis.The simulation conditions are listed as follows:

(i)The overall powerP=2,Alice and Bob take up half of the overall power,i.e.,PA=PB=0.5P=1,the pilot power ratio of Alice and Bob are equal and is denoted byα.Then the pilot power isPT=αPB,user data power isPX=(1−α)PA,whereα ∈[0,1].Define the signal to noise ratio(SNR)of a receiver as30dB.

(ii) The pilots areTA=TB=The input signals are modulated by MPSK,i.e.,whereM=2,4,8,16.

(iii) The channelVfollows complex Gaussian distribution with zero mean and variancePV=σ2V=1,i.e.,V ～CN(0,1).

(iv) The additive noises follow the same complex Gaussian distribution with zero mean and varianceσ2N,which is calculated by the definition of SNR in condition(i).

The simulations are carried out as follows.

(i) SetP=2,PA=PB=0.5P=1,M=2,4,8,16,and pilot power ratioα ∈[0,1].

Figure4.The effects of pilot power ratio on data rate and endogenous secret key rates.

(ii)The noise varianceσ2Nis calculated according to the SNR definition in condition(i).The channelVand noises(NAT,NBT,NAX,NBX)are generated according toV ～CN(0,1) andNAT,NBT,NAX,NBX ～CN(0,σ2N).

(iv) Substituting the pilots,signals,and noises intoYAT=V TB+NAT,YAX=V XB+NAX,YBT=V TA+NBT,andYBX=V XA+NBX,we accomplish one observation.

(v)Repeating step(ii)to step(iv)for 106times,we get 106observations.Monte Carlo experiments with the Copula entropy method [41,42]are carried out with these observations to estimateH(YAT,YAX)andH(YBT,YBX).Let them minus the theoretical values ofH(YAT,YAX|XB) andH(YBT,YBX|XA) respectively to get the estimated values of uplink data rateRXUand downlink data rateRXD.The reason for utilizing partial estimation is to mitigate the estimation errors in Monte Carlo experiments.

(vi)Taking the simulation conditions into(20),(22),(23),(25),and(26),we get the corresponding theoretical values ofRKT,RKTX,RKXT,RKXin (2),and the overall secret key rateRK.

(vii)Changing(α,M,SNR)and repeating step(ii)to step(vi),we get the curves of the estimated data and secret key rates with(α,M,SNR),i.e.,Figure4.

We draw the following conclusions from Figure4.

(i)The secret key rates(RKT,RKTX,RKXT,RKX,RK) are non-negative,which means both the pilots and user data power can be utilized to extract secret keys.RKkeeps constant for a given SNR,that is because after having excluded the randomness of transmitted signals,XAandXBhave the same function as pilots.Hence,the overall secret key rate is equal to the case when Alice and Bob transmit pilots with all the power they have.

(ii)Whenα=0.5,data rateRXgets its maximum value,which is equal to the optimal power ratio determined by the upper bound analysis,validating the theoretical analysis.

(iii)For a given SNR,whenα=0,Alice and Bob allocate all of their power to sending user data and no pilots are transmitted.Therefore,ratesRKT,RKTX,RKXTequal to 0,whereas rateRKXgets its maximum value.Whenα=1,Alice and Bob allocate all of their power to sending pilots and no user data is transmitted.Therefore,ratesRKTX,RKXT,RKXequal to 0,whereas rateRKTgets its maximum value.

(iv)For a given SNR,whenα ∈[0,1],the power of pilots increases withα,whereas the power of user data decreases.Hence,RKTincreases butRKXdecreases.Meanwhile,YATandYBX|XA(YBTandYAX|XB)are correlated.Therefore,ratesRKTXandRKXTare non-negative.To be more specific,whenαis small,the randomness of the wireless channel inYATandYBTare not fully extracted,some common randomness could be extracted from the power of pilots and user data.Hence,RKTXandRKXTincrease from 0 first.Asαincreases,pilot power increases,increasing the ability of Alice and Bob to extract the randomness of the wireless channel from pilot power.However,the power of user data decreases,reducing the ability of Alice and Bob to generate secret keys from the power of pilots and user data,thus decreasingRKTX,RKXT.

(v) When the optimal power allocation scheme is adopted,i.e.,α=0.5,the keys ratioRKT/RKincreases with SNR.That is because when SNR is high,Alice and Bob can estimate wireless channels much more accurately than in the low SNR case.That is to say,Alice and Bob are more capable of extracting keys from channel randomness with pilot power,whereas the introduction of user data power does not bring in much increase in secret key rates.

(vi) For a givenα,RXD,RXU,RKT,RKTX,RKXT,andRKXincrease with SNR,the reason is that the effects of additive noise on communication and secret keys generation decrease with SNR.The maximum value ofRKTXandRKXTarrive at smallerα,that is because when SNR increases,Alice and Bob become more able to extract the randomness of the wireless channel from pilot power.This corresponds to Conclusion 3 in Section III.

5.2 The Maximum Data Rate and Secret Key Rate

This section undertakes simulations under the optimal power allocation scheme to exhibit the relationship between the secret key rate and the maximum data rate with SNR andM.The simulation is undertaken with the same conditions as Section 5.1 and carried out with the following steps.

(i)Set the overall powerP=2,Alice and Bob have equal powerPA=PB=0.5P=1,M=2,4,8,16,pilot power ratioα=0.5,and SNR∈[0,30]dB.

(ii) Repeating the steps from step (ii) to step (v) in Section 5.1,we get the estimated data rate under given conditions.Then,substitute current conditions into(20)and(26)to calculateRKTandRK.

(iii)Changing(SNR,M)and repeating step(ii),we get Figure5,which represents the relationship between the maximum data rate and the secret key rate with SNR andM.

According to Figure5,we draw the following conclusions.

(i)WhenM=2,4,8,the secret key rate is always larger than the data rate;whenM=16,the secret key rate nearly matches the data rate.Therefore,it is possible to protect the MPSK modulated user data via the endogenous secret keys.

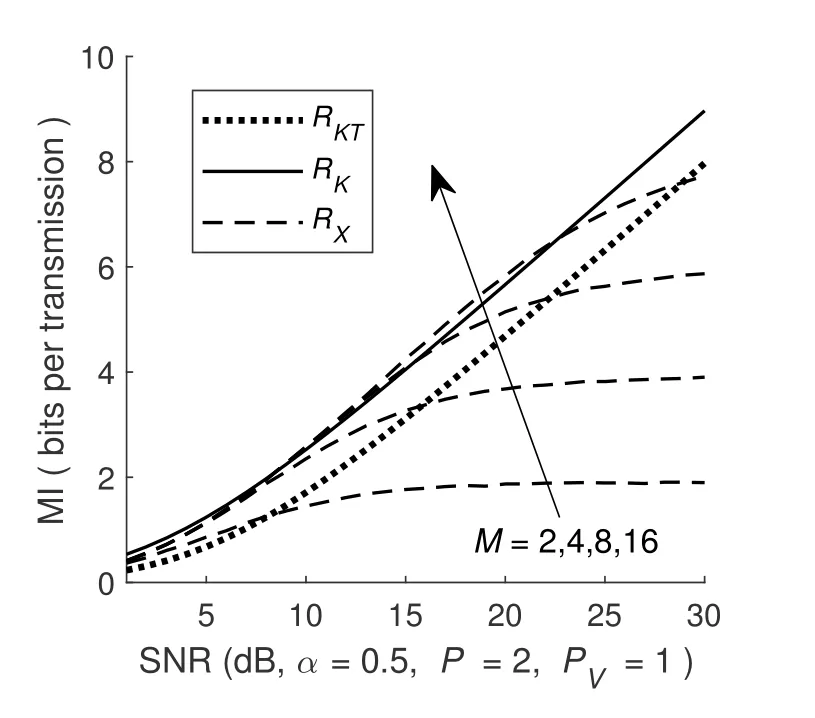
Figure5.Curves of the maximum data and secret key rates with SNR and M.

(ii) The data and secret key rates increase synchronously with SNR.That is because when SNR increases,the effects of additive noises on communication and secret keys generation are mitigated a lot.Therefore,wireless communication has an automatic matching property for the endogenous secret key rate and the maximum data rate.

(iii) For a given modulation numberM,the data rate increases before keeping stable at the level near 2 log2(M).That is because when SNR is small,the transmission capacity of the wireless channel is smaller than the transmitting rate from the source,i.e.,the data rate is limited by the transmission capacity of the wireless channel.The transmission capacity increases with SNR,which improves the data rate.When SNR is large enough,the data rate approaches the transmitting rate of the source,i.e.,2 log2(M),after which the data rate is limited to the transmitting rate of the source,thus keeping stable.That is the reason why theRXlines(M=8,16)overlap in Figure4 (a) and theRXlines (M=4,8,16) overlap when SNR is small in Figure5.

(iv)For the given SNR(like 15dB),the data rate increases at first and then keep stable withM.That is because whenMis small,the transmission capacity of the channel is bigger than the information quantity carried in the modulated MPSK symbol.AsMincreases,the information quantity that MPSK symbols carry approaches the channel’s transmission capacity gradually,increasing the data rate.After that,the data rate remains steady withM.That is because when the information quantity exceeds the transmission capacity of the wireless channel,receivers cannot distinguish the nearby MPSK constellations.

(v)RK >RKTis always true,which indicates that the proposed keys generation scheme via the received signals of both pilots and data outperforms the traditional keys generation method via received pilot signals.The increments makeRKandRXmatch each other.

Based on the results in sections 5.1 and 5.2,we can conclude that secret keys can be generated from the power of pilots and user data in wireless communication.Furthermore,it is possible to make the maximum data rate match the overall endogenous secret key rate,thus achieving perfect real-time encryption without decreasing the data rate.It should be noted that though this model investigates the systems with one pilot symbol along with one user data symbol and the rates of data along with secret keys are not that high,the endogenously secure data rate can be improved linearly by introducing independent wireless channels in the domains of frequency,space,or time.

VI.CONCLUSION

This paper proposes an endogenous security solution to the inherent security problems in wireless communication.First,we apply information theory to analyze the endogenous wireless security principle qualitatively,based on which we propose that it is possible to make the endogenous secret key rate nearly match the maximum data rate in fast-fading scenarios.Second,we verify the proposition in an instantiation system.Theoretical analysis and simulation results indicate that wireless communication has endogenous security functions to achieve perfect encryption for the user data emitted at the maximum rate.Besides,we can achieve high-speed endogenously secure data rates by introducing independent wireless channels in the domains of frequency,space,or time.Finally,we point out that this paper investigates endogenous wireless security via secret keys in fast-fading scenarios.Endogenous wireless security in slow-fading scenarios is under investigation.Future work will focus on analyzing the effects of channel correlation and validating the feasibility of the scheme in scenarios with interferences.

ACKNOWLEDGEMENT

This research was funded by the National Key R&D Program of China under Grant 2017YFB0801903,the National Natural Science Foundation of China under Grant 61871404,61701538,61521003,and Doctoral Fund of Ministry of Education of China under Grant 2019M663994.Part of the results was published by the IEEE ICCC 2020[40].

APPENDIX A PROOF OF THEOREM 1

The probability density function(PDF)of the complex Gaussian random vector X=(X1,X2,···,Xn)Twith the mean vectorµand the covariance matrix K is

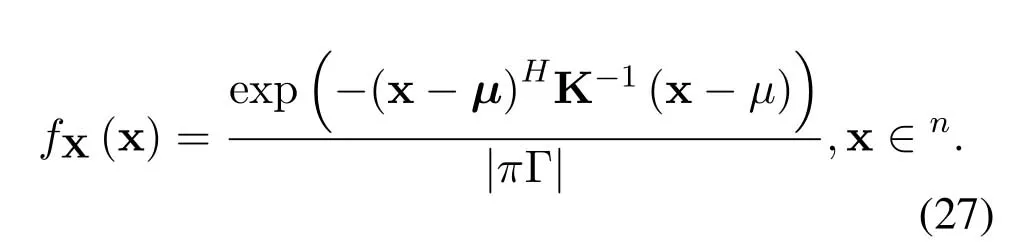
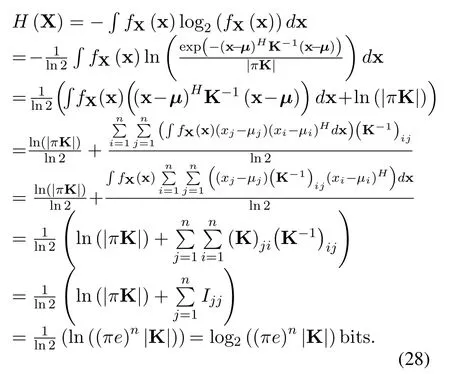
That is the end of the proof for Theorem 1.

APPENDIX B PROOF OF THEOREM 2

This appendix proves that the random variableY=V/X+Nfollows complex Gaussian distribution whenXis modulated by MPSK andVas well asNfollow complex Gaussian distributions.First,we derive the distribution of the real part and imaginary part ofV X,after which we calculate the distribution ofY=V X+N.

The complex Gaussian random variableV,N,Xcan be expressed aswhereis constant,θX ∈ {θX(1),θX(2),...,θX(M)},θX(i)∈[0,2π],0

For the convenience of proof,we introduce Lemma 1.

Lemma 1.If random variable T follows uniform distribution in[0,2π],then for any number a in[2kπ,2(k+1)π],with k being a natural number,the probability density function of random variable Y=cos(T+a)and Y=sin(T+a)is

Proof.The distribution ofY=cos(T+a)is derived at first.SetX=T+a,thenXfollows uniform distribution in[a,a+2π].As the distribution ofYvaries witha,different conditions are discussed as follows.

(B.1)When 2kπ cos(a),and−1≤y≤1,we have

(B.2)When 2kπ

(B.3)When 2kπ+π cos(a),and−1≤y≤1,we have

(B.4)When 2kπ+π

Based on the discussions given in (B.1),(B.2),(B.3),(B.4),we have the PDF ofY=cos(T+a)is

AsY=sin(T+a)=cos(T+a −π/2),setb=a −π/2,then we have the probability density function ofY=sin(T+a) which is the same as(T+a)according to Lemma 1.

The end of the proof of Lemma 1.

Now we turn to demonstrateU=V X=UR+iUI=SV Xcos(θV+θX)+iSV Xsin(θV+θX)follows complex Gaussian distribution.As the analysis process ofURandUIis the same,without losing generality,we utilizeURas an example to deduce the probability density function.According to the formula of full probability,we have

As

Therefore,uR|θX=θX(i)Substituting(39)into(38),we have

That is the end of the proof for Theorem 2.

APPENDIX C

This appendix gives the derivations mentioned in the paper.