M-BCJR Algorithm with Channel Shortening Based on Ungerboeck Observation Model for Faster-than-Nyquist Signaling
Hui Che,Yong Bai
1 School of Information and Communication Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China
2 School of Information and Communication Engineering,Hainan University,Haikou 570228,China
Abstract:The M-BCJR algorithm based on the Ungerboeck observation model is a recent study to reduce the computational complexity for faster-than-Nyquist (FTN) signaling [1].In this paper,we propose a method that can further reduce the complexity with the approximately same or better bit error rate(BER)performance compared to[1].The information rate(IR)loss for the proposed method is less than 1%compared to the true achievable IR (AIR).The proposed improvement is mainly by introducing channel shortening(CS)before the M-BCJR equalizer.In our proposal,the Ungerboeck M-BCJR algorithm and CS can work together to defeat severe inter-symbol interference (ISI) introduced by FTN signaling.The ISI length for the M-BCJR algorithm with CS is optimized based on the criterion of the IR maximization.For the two cases τ=0.5 and τ=0.35,compared to Ungerboeck M-BCJR without CS benchmark [1],the computational complexities of Ungerboeck M-BCJR with CS are reduced by 75%.Moreover,for the case τ=0.35,the BER performance of Ungerboeck M-BCJR with CS outperforms that of the conventional M-BCJR in[1]at the low signal to noise ratio region.
Keywords:M-BCJR;Ungerboeck model;channel shortening;FTN;reduced-complexity;turbo equalization
I.INTRODUCTION
In the future communication system,high spectrum efficiency (SE) is required because of the explosive growth of data traffic.Faster-than-Nyquist(FTN)can improve the SE by packing the transmission interval of the neighboring shaping pulses.Still,it introduces inter-symbol interference(ISI)due to the violation of the Nyquist zero-ISI theorem.In addition to increasing the constellation cardinalityψ,reducing the time packing ratio (TPR)τcan also increase SE.As the TPRτtends to zero,the information rate of the FTN system with binary input converges to the constrained capacity [2]with Gaussian input [3].Smaller TPR results in a higher rate FTN system [4].Prlja and Anderson have investigated the high rate FTN in [5],whereτ=0.5 and 0.35.The complexity of the maximum posterior probability(MAP)equalizer for FTN isO(ψLI),whereLIis the ISI length.The ISI lengthLIis very long for high rate FTN and the original Bahl-Cocke-Jelinek-Raviv (BCJR) algorithm equalization become unmanageable because of high-complexity.To our best knowledge,there are mainly six approaches proposed so far to reduce the computational complexity involved in FTN systems.We summarize them as follows.Firstly,the simplest solution is that the BCJR equalizer works with a truncated version of the channel response[6],and it may yield poor bit error rate(BER)performance unless the truncated part of the channel response has negligible power.Secondly,linear pre-equalization (LPE)[7]makes the FTN equivalent to an orthogonal transmission.However,the method LPE failed whenτ <1/(1+βr),whereβris the roll-off factor of root raised-cosine(rRC)pulse.Thirdly,a frequency-domain equalization(FDE)based on minimum mean square error(MMSE)criterion is employed for FTN[8].The optimal equalization criterion is the MAP criterion rather than the MMSE criterion.The FDE fails to reliably detect the higher rate FTN signal,while the time-domain equalization still performs well [9].Fourthly,the sumproduct algorithm(SPA)[10]for FTN makes the complexity increase linearly with the number of interferers.The SPA is not suitable for high rate FTN due to too long ISI length.Fifthly,the M-BCJR based on the Forney observation model [11,5]or Ungerbocek observation model[1]select a portion states of all states.For high rate FTN,the symbol rate exceeds the signal bandwidth and the whitening filter cannot be directly derived for M-BCJR based on the Forney observation model [1].In [5],the whitening filter is replaced by an all-pass filter and the model is converted to super minimum phase.However,the method in[5]needs 3 recursions and the stability of the turbo loop is very sensitive to the loop gain and the block length.The M-BCJR based on the Ungerboeck observation model[1]accepts the colored noise and selects the bestMstates based on the MAP rule by taking some future symbols into account.It is referred to as the Ungerboeck M-BCJR method in this paper.Sixthly,the channel shortening(CS)[12,13]uses an informationtheoretic framework to reduce the ISI length for the original BCJR equalizer.The complexity of CS-BCJR isO(ψLr),whereLris ISI length of the target response.However,the CS-BCJR equalizer cannot offer satisfactory BER performance with a smallLrfor high rate FTN.
To further reduce the complexity involved in the FTN signaling,we propose an improvement for the Ungerboeck M-BCJR method by employing the CS before the Ungerboeck M-BCJR equalizer.In this proposal,we optimize the ISI length of target responseLrfor Ungerboeck M-BCJR equalizer with CS based on the information rate(IR)criterion.The two results forτ=0.5 and 0.35 turn out that our proposal can reduce the receiver complexity and achieve the approximately same or better BER performance compared to [1].CS is a technique proposed initially by Falconer and Magee in 1973[14]and recently improved in[12]for general linear channels,such as MIMO and ISI channels.The optimal front-end filter and target response of CS can be formulated in the closed-form [12]by using an information-theoretic framework.Huet alin [15]use the same method as [12]to optimize the prefilter (channel shortener) by maximizing the mutual information lower bound.The FOM shortener in[15]employs the Forney observation model,while the UBM shortener in[12]uses the Ungerboeck observation model.The parameters in [15]and in [12]are optimized with the assumption that the input is Gaussian,and then these optimized parameters are applied to the finite alphabet inputs directly.They do not consider further the parameter optimization for the finite alphabet input,such as the ISI length.For the CS in[12],the ISI lengthLrshould be determined firstly.However,there is no literature on the optimization of the ISI lengthLrfor CS by far.FTN signaling does not affect the minimum Euclidean distance(MED)of uncoded binary sinc pulse transmission,and hence the asymptotic error probability in theory,as long as the TPFτis above the Mazo limit [16–19].Therefore,many past papers analyzed and optimized the FTN system based on the MED criterion or Mazo limit.However,the MED is not a robust and reliable metric[20].Maximizing MED between the constellation points,unfortunately,could not ensure a large achievable IR (AIR) and AIR considers the Euclidean distance set beside the MED in [20].For the first time,we optimize the ISI lengthLrfor CS based on the IR criterion.For the finite alphabet,the AIR of the ISI channel and its bounds based on auxiliary channel(or mismatched channel)have been studied in[21–23].AIR calculation can use a larger ISI length to achieve the true AIR and a smaller ISI length may cause IR performance losses.There is a trade-off between complexity and performance.The lower bound on the true AIR is achievable by a maximum-likelihood equalizer with the same ISI length[21,23,12].The calculation of the lower bound needs a smaller ISI length than true AIR calculation.In this paper,the ISI lengthLrfor Ungerboeck M-BCJR equalizer with CS is optimized according to the criterion that the lower bound on true AIR (ILB(Lr)) is close to the true AIR (I(X;Y)).The method minimizes ISI length with the IR performance loss less than 1%compared to the true AIR,i.e.,I(X;Y)−ILB(Lr)≤∆Iand ∆I=1%×I(X;Y).Due to the iteration between the FTN equalizer and the channel decoder,more computational complexity can be saved by our method.The Ungerboeck M-BCJR equalizer takes advantage of CS to make a flexible trade-off between BER performance and complexity.
We use the IR performance to optimize the ISI lengthLrfor CS by(24).We use BER performance to verify the effectiveness of the proposed algorithm,i.e.,the proposed algorithm has the approximately same or better BER performance compared to the conventional method in [1].In summary,we have the following main contributions in this paper.
• We propose an improvement for the Ungerboeck M-BCJR method to further reduce computational complexities.The improvement is the introduction of a channel shortening (CS) before the MBCJR equalizer.
• We optimize the ISI length for M-BCJR with CS based on the IR criterion to reduce the receiver complexity.Our proposal has the approximately same or better BER performance compared to[1]after such an optimization.
The paper is organized as follows.Section II presents the proposed system model of FTN.Section III discusses the M-BCJR algorithm with channel shortening.Section IV investigates CS optimization based on IR criterion.Section V provides the simulation results.Section VI offers concluding remarks.
II.SYSTEM MODEL
Figure.1 shows the baseband FTN system model.In the transmitter,Kinformation bits u=[u1,···,uK]Tare encoded by a (N,K) binary channel encoder to yield a lengthNcodeword c=[c1,···,cN]T,whereci ∈{0,1}.The code rate of the channel encoder isr=K/N.The codeword c is permuted by a random bit-interleaver with interleave lengthN.The output of bit-interleaver,d,feeds a signal mapper.Assuming that binary phase shift keying(BPSK)signaling is employed,i.e.,ψ=2,the output of signal mapper is a length-Nsymbol sequence x=[x1,···,xN]T,wherexi ∈{+1,−1}.The symbol sequence x is delivered to the FTN modulator,where the shaping pulse ish(t).TheT-orthogonal rRC pulse with a roll-off factorβr=0.3 is employed as the shaping pulseh(t).In order to maintain almost the same power spectral density(PSD),the shaping pulseh(t) has a time-truncation to±ζTaroundt=0,whereζ=15 in this paper.The rRC pulse with the favorable time-truncation has a very low out-of-band emission.The FTN signal can be expressed as
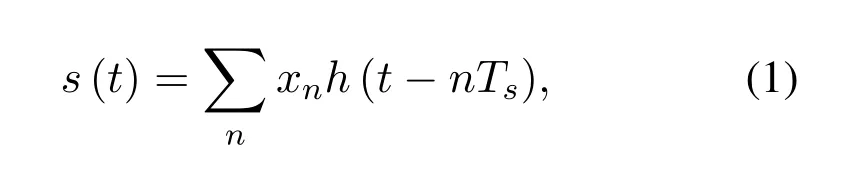
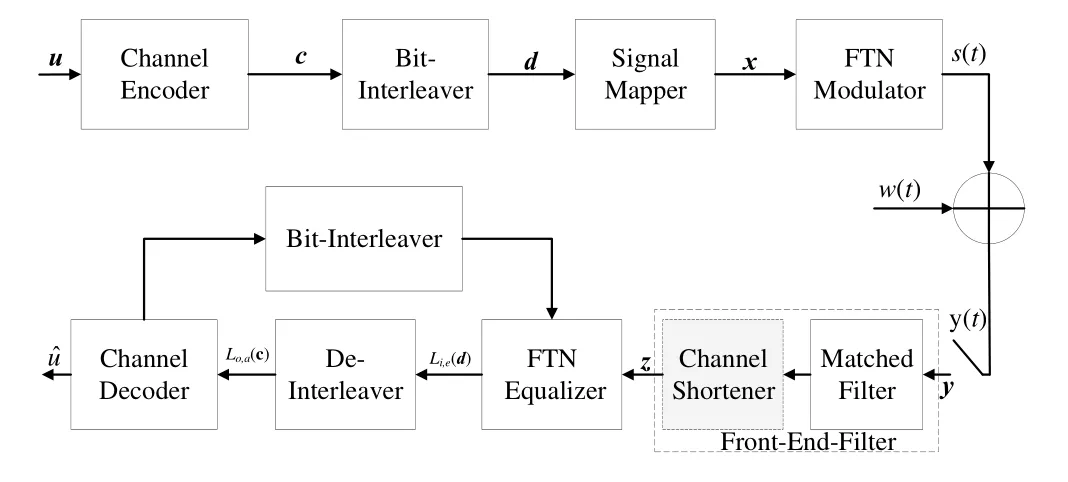
Figure1.System model for high rate FTN.
where the FTN symbol periodTs=τTand the sampling period must be less than or equal toT/(1+βr).In this paperτ≤1/(1+βr),the sampling period equals the FTN symbol periodTs.The shaping pulseh(t) has unit energy,i.e.∞−∞|h(t)|2dt=1,and its double-sided bandwidthW=(1+βr)/T.It is obvious that(1)constitutes symbolic convolutional coding over the real field.Meanwhile,(1) is a filtering process,and it can be treated as ISI.Hence,the equalization of the FTN system with ISI is equivalent to decoding the convolutional code in the real field.
The FTN signals(t)is transmitted over the AWGN channel,and the received signal is given byy(t)=s(t) +w(t),where the white Gaussian noisew(t)has double sides PSDN0/2.
The receiver employs a reduced-complexity MBCJR equalizer based on the Ungerboeck observation model[24,25]together with the CS method.The CS method contains a front-end-filter hrand a target response gr.In the receiver,the received signaly(t)is sampled everyTsseconds.The sampled signal y pass through the front-end-filter hr,which consists of a matched filter and channel shortener.As shown in Figure.1,the difference between the receiver with CS and without CS[1]is that a channel shortener is introduced after the matched filter.The M-BCJR algorithm based on the Ungerboeck observation model accepts the target response grinstead of g as the ISI channel,wheredtin[1],g−l=glfor|l|≤LIandgl=0 for|l| >LI.The FTN equalizer works on the mismatched channel model and the mismatched conditional probability distribution function[25]
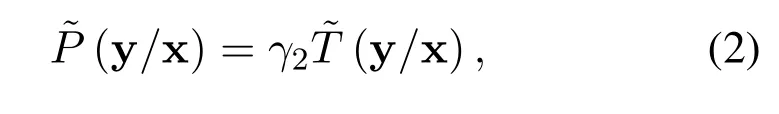
whereγ2[25]is independent of x,

(·)†denotes Hermitian transpose andNris the mismatched noise density [12],ykis the sampled value in y,Hrand Grare Toeplitz matrices corresponding to hrand gr[12],respectively.The definition of the matrix Gris as follows
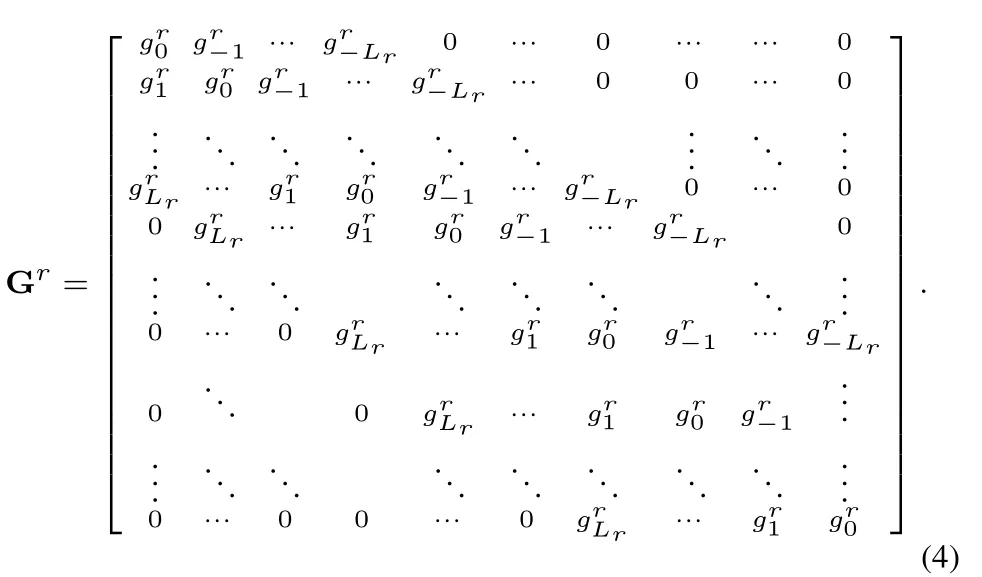
Hrhas the same form as Gr.The mismatched channel law
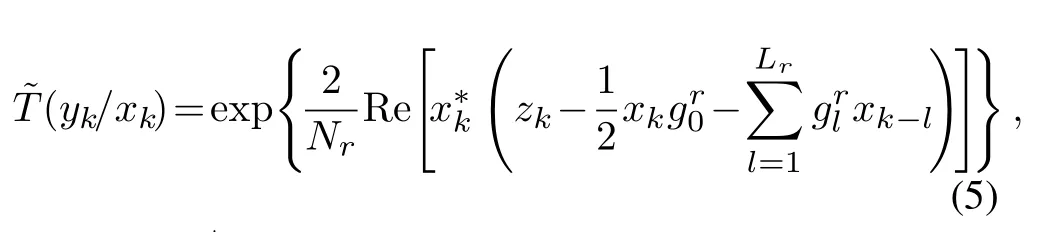
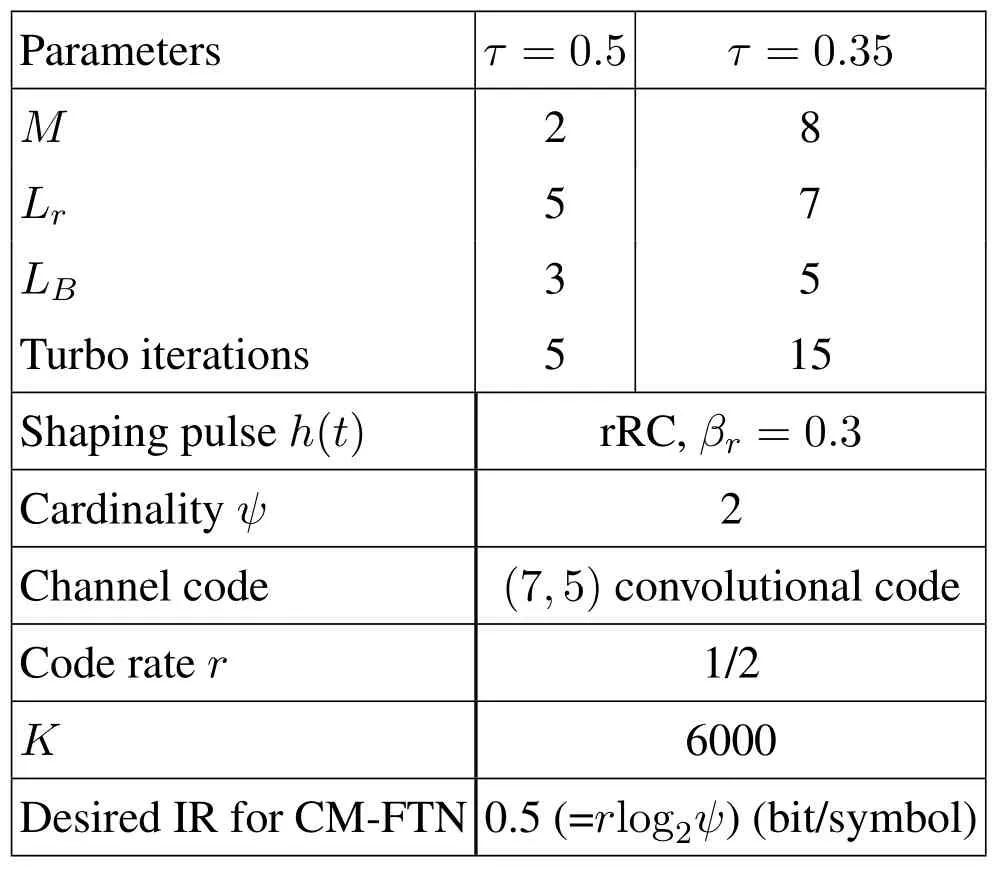
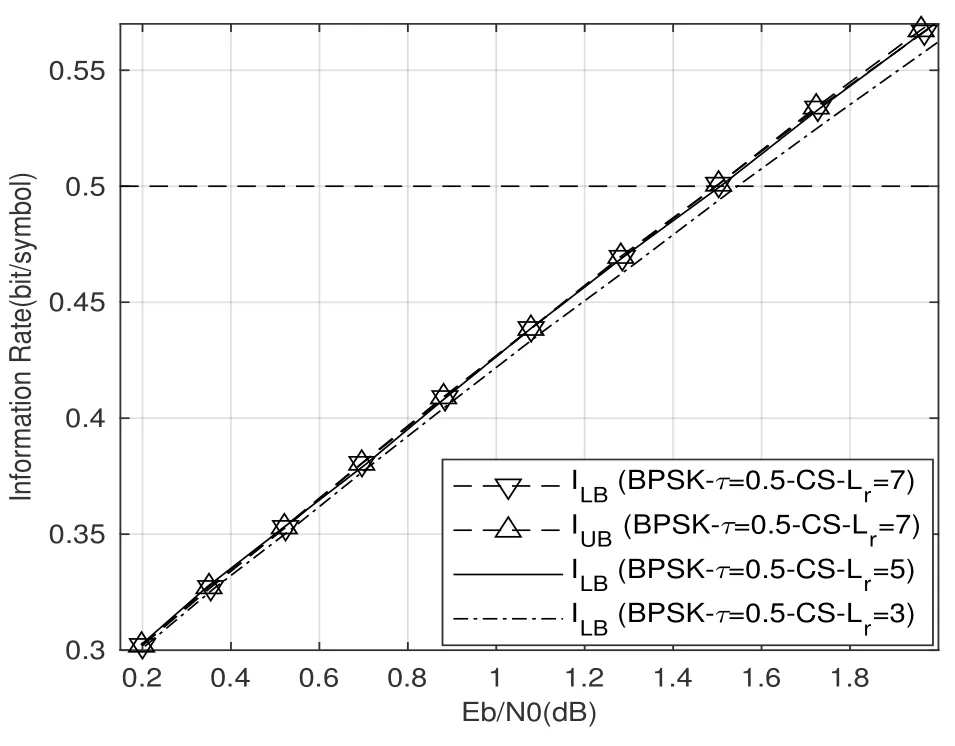
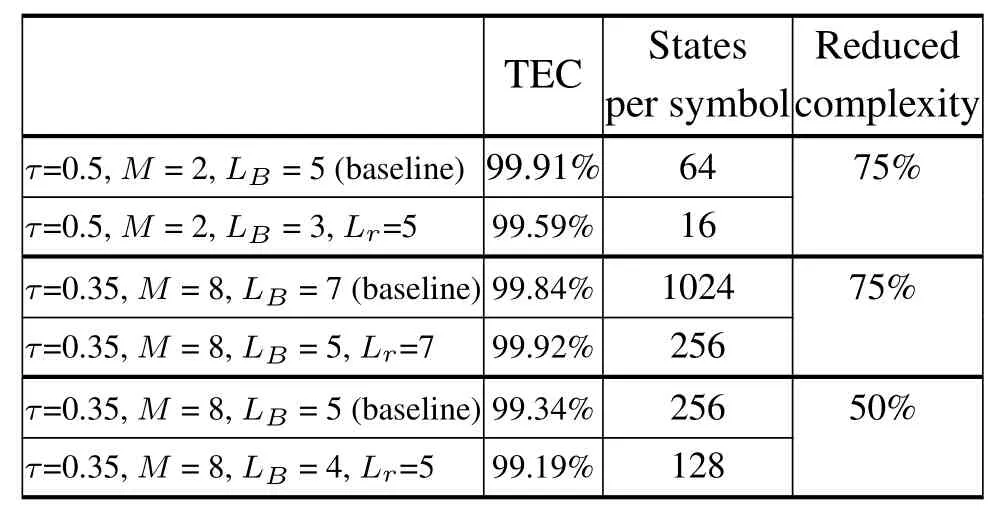
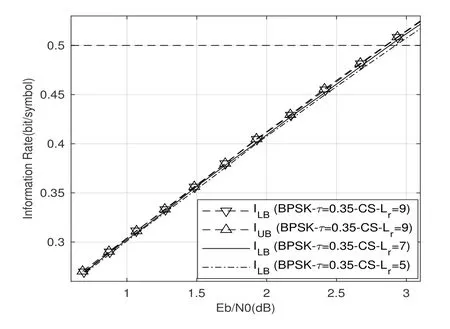
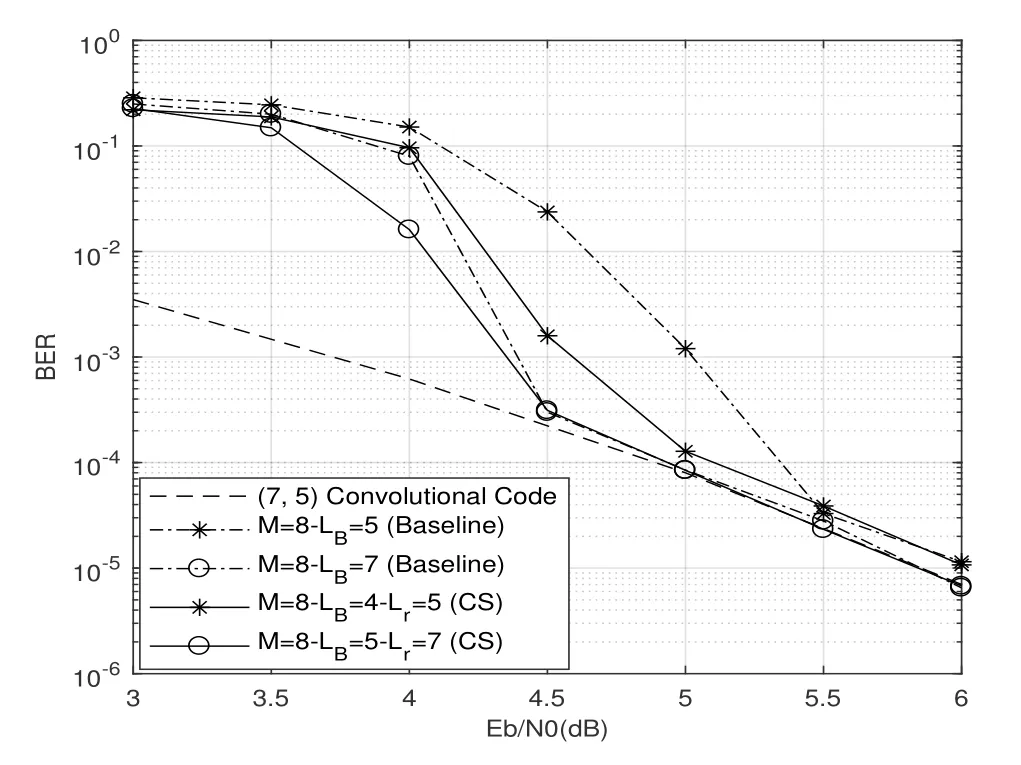
where (·)∗stands for conjugate,zkis the output of front-end-filterfor|l|≤Lr,grl=0 for|l| >Lr,Lris the ISI length.The ISI length for the original Ungerboeck M-BCJR algorithm without CS isLI,whereLI=2ζ/τ」and·」representsflooroperator.The Ungerboeck MBCJR algorithm with CS can further reduce complexity whenLr The transmitter can be seen as a serially concatenated code(SCC).The channel encoder severs as outer code.The cascade of signal mapper and FTN modulator servers as inner code.The log-likelihood ratio(LLR) values are passed between the inner and outer code detector.After several iterations,a sequence ˆu can be found,which is regarded as the estimate of u. The main work of CS is calculating the front-end-filter hrand target response gr,which is achieved in the frequency domain.[H0,···,HNF −1]=FFT(h),where FFT means fast Fourier transform,channel impulse response(CIR)h={hk}andhk=h(kTs)forτ≤1/(1+βr).The FFT sizeNFis larger thanLI.In this paper,the CIR is real andHNF −k=H∗k,fork ≥1.More details of implementation for calculating hrand gr[13]are as follows, step 1.Compute the real sequence Γ=[Γ0,···,ΓNF −1] where 0≤k≤NF −1 andHNF −k=Hkfork ≥1. step 2.Compute the real sequence V=[V0,···,VNF −1] The real sequence v=[v0,···,vNF −1]=IFFT(V),whereIFFTmeans inverse fast Fourier transform andvNF −k=vkfork ≥1.TheFFTandIFFTsize are bothNFin this subsection.¯v is part of v and=[v1,···,vLr].The symmetric Toeplitz matrix=Toeplitz([v0,···,vLr−1]) whose first row is[v0,···,vLr−1]andLr≤LI≤NF. step 3.Compute the real sequence e=and real-valued scalar step 4.Obtain the 1×(Lr+1)real sequence and U=[U0,U1,···UNF −1]=FFT([u,01×(NF −Lr−1)]). step 5.Compute the frequency response for target response where 0≤k≤NF −1 andGrkfork ≥1.and the time response for target response step 6.Compute the frequency response for frontend-filter where 0≤k≤NF −1 andHrNF−k=(Hrk)∗fork ≥1.The frequency response for frontend-filter here is different from that in [13].Hkin [13]is replaced byH∗kin (11) andH∗krepresents the frequency response of the matched filter.and the time response for front-end-filter hr= The front-end-filter hrexecutes interference cancellation to make the energy of the CIR more concentrated,and the target response approximates the overall CIR.The channel shortener and the target response are optimal when the input symbols are circularlysymmetric complex Gaussian[12].Figure.2 shows an example of the CS applied to the FTN system withτ=0.5.The optimal target response gris assumed to be of lengthLr=5,and the original channel g is of lengthLI=60.The CS makesgrl=0 for|l| >5.However,the original channel has a non-negligible coefficient atl=7.ISI phases vary after CS,and the target response has fewer zeros on and outside the unit circle compared to the original channel.The CS enables the energy of the final CIR more concentrated in the time domain. Hereα,βandγhave the same notation as the Ungerboeck M-BCJR algorithm without CS [1]for forward recursion metric,backward recursion metric and branch metric,respectively.Ungerboeck MBCJR algorithm with CS is described as follows.σnis the set of states at trellis sectionnandσn=(xn−Lr+1,···,xn).For anyi ∈σn−1andj ∈σn,the metric of the branch connecting statesiandj Figure2.Example of the CS applied to the FTN system with τ=0.5. The forward variable is computed recursively in a forward trellis pass according to whereσn−1is the set of states that can reach statejat stagen.The forward recursionαis computed from theMnonzero values retained inσn−1.If the backward search is limited toLBsymbols,then backward recursion metricβbecomes whereχ(·) represents all the combinations of a certain set[1].At each section,theβcomputation traces forward through some states that are already measured in the previous search.The probabilities of{σn+LB}rooted fromσnafter eachβcomputation are saved and used in the next trellis section [1].The states corresponding to each input symbol isMψLB.The posteriori probability of stateσnand the LLR value for BPSK signaling isL(xn)which is expressed as whereσ+1andσ−1represent the states induced by inputxn=+1 andxn=−1,respectively.With the a posteriori probability of eachσn,it is straightforward to choose theMmost possible states. For BPSK signaling with a particular ISI pattern gr,the correct-path-loss (CPL) free condition [1]for MBCJR with CS is wheregrl=0 for M-BCJR with CS when|l|>Lr.If(17) is true,the algorithm withM=1 is performed error-free in the absence of noise,since the correct path always has the largest metric[1].CPL free condition implies the close relationship betweenLBandM,wherein a larger value ofLBenables a smaller value ofM,and vice versa.It is obvious that proper choices ofMandLBensure CPL-free performance.In order to reduce the complexity,LI >LBandM ≥2 in[1].LI >Lr >LBandM ≥2 in this paper.We use the time energy concentration (TEC) in the time interval[−LB,LB]to measure the reliability ofLBused by the backward recursion metricβ.The TEC is defined as follows Forτ=0.5 as shown in Figure.2,Cgr(LB=3)=99.59% for M-BCJR with CS (Lr=5).Similarity,Cg(LB=3)=99.36%for M-BCJR without CS(LI=60).With the sameLB,M-BCJR with CS has a larger TEC than M-BCJR without CS,i.e.,M-BCJR with CS has a better energy concentration performance at the time domain.LBis subject toLB≤Lr,andLrneeds to be further optimized.The complexity of calculating backward recursion metricβin(14)is reduced by minimizingLr.The decrease inLrmay result in a performance loss.Therefore,we proposeLroptimization,that is,reduceLras much as possible without leading to noticeable IR performance loss.The optimization forLris suggested in IV,i.e.,CS optimization based on IR criterion. Comparisons to the method in[1].On the one hand,Ungerboeck M-BCJR without CS [1]needs a largerLBthan the proposed method,requiring more computational complexity for calculating backward recursion metricβ.On the other hand,the set of states at trellis sectionnfor Ungerboeck M-BCJR without CS is=(xn−LI+1,···,xn).The method in [1]has(LI −Lr) addition operations corresponding to each input symbol more than our propose method for calculating the metric(yk/xk).Considering the iterations between the FTN equalizer and the channel decoder,the states ˆσandσneed to be updated at each trellis section in each iteration.The complexity of our proposal is greatly reduced compared to the methods in[1]. AsN →∞,the AIR[21,23]supported by the FTN system can be expressed as whereEY(·)denotes the expectation operator for the random variable Y,P(y/x) is the original channel law, and it can be computed by means of the simulationbased algorithm (SBA),i.e.,the forward recursion of the BCJR algorithm[21].The problem of computingP(y)is that the state spaces for the FTN channel are too large.The SBA works on a trellis withψLIstates per time index,which becomes computationally unmanageable for large values ofψandLI.Therefore,we need to resort to the study of bounds.Upper and lower bounds on the true AIRI(X;Y) [21][23]can be computed as follows From(19) to (23),we can find thatILB=IUB ⇔(y/x)=P(y/x)⇔IUB=I(X;Y) &ILB=I(X;Y).The law of the auxiliary channel in [12]does not considerγ2and is equivalent toin this paper.The lawdoes not qualify as a valid probability density function (PDF).The law of the auxiliary channel is a significant quantity for the tightness of the upper and lower bounds.Unlike[12],this paper employs(2)as the law of the auxiliary channel to make the upper and lower bounds tighter and giving the AIRI(X;Y).is the smallestL,which yields the true AIR up to the accuracy of the plot.In the following,the values of IR(including the true AIR)are of limited precision(up to three decimal digits[21]). For coded modulation (CM) FTN with iterative decoding,the equalization complexity per iteration isO(ψLr),and the iterations increase computational complexity several times.For the FTN with a largerLr,the original BCJR algorithm detection becomes unmanageable due to high-complexity.The CS can reduce the ISI lengthLrfor the FTN equalizer.However,how to determine the value ofLrfor CS has not been studied in the relevant literature.In this paper,we minimize the ISI lengthLr=for CS such that where ∆I=1%×I(X;Y)and the value ofI(X;Y)is of limited accuracy.I(X;Y)−ILB(Lr)≤∆Imeans that the IR performance loss is not noticeable compared to true AIR.The lower boundILBon theI(X;Y) is achievable by a maximum-likelihood equalizer.The equalizer which employs the CS withhas the lowest complexity without noticeable IR performance loss.This optimization can offer satisfactory performance with reasonable complexity for FTN. To verify the effectiveness of the proposed algorithm,the Ungerboeck M-BCJR algorithm with CS,it’s BER performance and complexity are compared with that of the M-BCJR algorithm without CS in[1](as baseline).The parameters for CM-FTN systems with CS are listed in Table1.The same parameters with [1]are used,i.e.,the (7,5) 4-state rate-1/2 nonrecursive convolutional code,information sequence lengthK=6000,M=2 forτ=0.5 andM=8 forτ=0.35.Before performing BER simulation,we must first determine the parameterLrfor CS by the method in Section IV,then determine the parameterLBof Ungerboeck MBCJR. CS optimization for BPSK-FTN withτ=0.5 is shown in Figure.3.It shows the results for the suggested boundsILBandIUBgenerated by using SBA with CS.The CS bounds withLr==7 yield the true AIRI(X;Y)=0.5 bit/symbol up to the accuracy of the plot [21]atEb/N0=1.496 dB.The rate 0.5 bit/symbol is the desired IR for the CM-FTN with code rater=0.5 and BPSK at the particularEb/N0=1.496 dB.The CS method can use a smaller ISI lengthLrto make the upper and lower bounds tighter and giving the true AIRI(X;Y)=0.5 bit/symbol.We can find a minimum ISI lengthLr==5 for CS withτ=0.5 such that0.0015<∆Iat the particularEb/N0=1.496 dB,where ∆I=1%×I(X;Y)=0.005 bit/symbol.The FTN system based on CS with minimum ISI lengthhas a little IR performance loss. Table1.Parameters for CM-FTN. Figure3.CS optimization for BPSK-FTN with τ=0.5 based on IR criterion.The CS optimization method gives the true AIR I(X;Y) with =7 and =5 for desired IR=0.5 bit/symbol. Figure4.BER results of the BPSK modulated FTN system with(7,5)convolutional code for τ=0.5 and 5 Turbo iterations. Table2.TEC and complexity comparison between the proposed method and the baseline in[1]. After determiningLr==5,we need to determine the value ofLBfor Ungerboeck M-BCJR.We found a reasonableLB=2 for Ungerboeck MBCJR in our simulations.The BER results for the case ofτ=0.5 are illustrated in Figure.4.The error performances of the baseline in Figure.4 are from Figure.7 in[1].The baseline withM=2,LB=5 outperforms the method in[12]withv=5[1].As the figureillustrates,the BER performance of our method withM=2,LB=3,Lr=5 is approximately equal to that of the baseline withM=2,LB=5 in [1].The states for our method and the baseline are listed in Table2.Compared the baseline,the complexity of the backward recursion metricβfor our method is reduced by 75%.The detailed complexity analysis is introduced in [1].Our method (Lr=5) can save 91.67% addition operations for calculating the metric ˜T(yn/xn)at each trellis section in each iteration comparing to the baseline(LI=60). CS optimization for BPSK-FTN withτ=0.35 is shown in Figure.5.The CS bounds withLr=LAIRopt=9 yields the true AIRI(X;Y)=0.5 bit/symbol forτ=0.35 atEb/N0=2.85 dB.The minimum ISI lengthLr==7 for CS withτ=0.35.As shown in Figure.5,at the particularEb/N0=2.85 dB,where ∆I=1%×I(X;Y)=0.005 bit/symbol.ILB(Lr=7) has a little IR performance loss compared to the true AIRI(X;Y).We useLr=LCSopt=7 andLB=5 for BER simulation for BPSK-FTN based on CS withτ=0.35.We use another set of parameters that are not optimized for comparison,Lr=5 andLB=4. Figure5.CS optimization for BPSK-FTN with τ=0.35 based on IR criterion.The CS optimization method gives the true AIR I(X;Y) with =9 and =7 for desired IR=0.5 bit/symbol. Figure6.BER results of the BPSK modulated FTN system with (7,5) convolutional code for τ=0.35 and 15 Turbo iterations. For the severe ISI caseτ=0.35,the BER results for FTN based on M-BCJR with CS are shown in Figure.6.The error performances of two baselines in Figure.6 are from Figure.8 in[1].The error performance of the baseline A(M=8,LB=7)is 1 dB better than that of the method in[5]withM=16 at 4.5 dB.The baseline B (M=8,LB=5) outperforms the method in [12]withv=7 [1].The BER performance of the suboptimal method B (M=8,LB=4,Lr=5) outperforms that of the baseline B[1]in the range of 3 to 5.5 dB.The complexity of the suboptimal method B is reduced by 50%compared to that of the baseline B.The BER performance of the proposed method A(M=8,LB=5,Lr=7)outperforms that of the baseline A in [1]in the range of 3 to 4.5 dB.Meanwhile,the complexity of the proposed method A is reduced by 75% for the backward recursion metricβ,which can be seen in Table2.The advantage for the combination of both M-BCJR and CS is that the Ungerboeck MBCJR based on CS can employ a smallerLBthan the conventional M-BCJR to achieve the approximately same BER performance.The complexity of Ungerboeck M-BCJR based on CS is lower than that of the conventional M-BCJR[1].The Ungerboeck M-BCJR based on CS can achieve better BER performance than the conventional M-BCJR[1]at the low signal to noise ratio (SNR) region.Besides,the proposed method A(Lr=7)can save 91.67%addition operations for calculating the metric ˜T(yn/xn)at each trellis section in each iteration comparing to the baseline (baseline A and B,LI=84). The TEC of the baseline A is better than that of baseline B,i.e.,99.84%>99.34%,which contributes to that baseline A has better BER performance than baseline B.There are two main reasons why the BER performance of the proposed method A is better than that of the suboptimal method B.On the one hand,the IR performance of the proposed method A is better than that of the suboptimal method B,which can be seen in Figure.5.On the other hand,the TEC of the proposed method A is larger than that of the suboptimal method B,99.92%>99.19% in Table2.The proposed method A and baseline B have the sameLB=5,but the proposed method A has a larger TEC than baseline B,i.e.,99.92%>99.34% in Table2.With the sameLB,M-BCJR with CS has a better energy concentration performance than M-BCJR without CS. In this paper,the Ungerboeck M-BCJR algorithm with CS is proposed for high rate FTN.We get the optimized ISI lengthfor FTN according to the criterion that theILBis close to theI(X;Y),i.e.,and ∆I=1%×I(X;Y).FTN equalizer acceptsas the minimum ISI length without noticeable IR performance loss.Unlike [12],this paper employs (2) as the law of the auxiliary channel to make the upper and lower bounds tighter and giving the AIRI(X;Y)with limited precision.The advantage for CS is that the channel shortener makes the energy of the channel impulse response more concentrated.Hence,the Ungerboeck M-BCJR based on CS can employ a smallerLBthan Ungerboeck M-BCJR without CS to achieve the same BER performance.Monte-Carlo BER simulations were carried out to verify the effectiveness of the proposed algorithm for high rate FTN.For the caseτ=0.5,the BER performance of our method is approximately equal to that of the method in [1]with 75%reduced complexity.For the caseτ=0.35,the BER performance of our method with M=8,LB=5 outperforms that of the method with M=8,LB=7 in[1]for the range of 3 to 4.5 dB.Meanwhile,the complexity of our method is reduced by 75%compared to the method in[1].In summary,our proposed method employing the optimized parameters can achieve the approximately same BER performance to the conventional method in [1]at moderate-to-high SNR with more reduced complexity.It is satisfactory that our proposed method achieves a better BER performance than the conventional method in [1]at the low SNR region with more reduced complexity. ACKNOWLEDGEMENT This work was supported by National Natural Science Foundation of China(No.61961014).III.M-BCJR ALGORITHM WITH CHANNEL SHORTENING
3.1 Channel Shortening
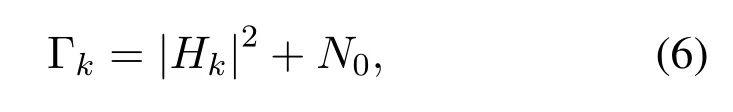


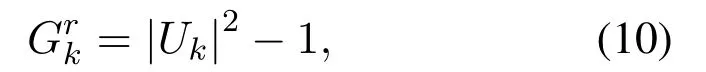
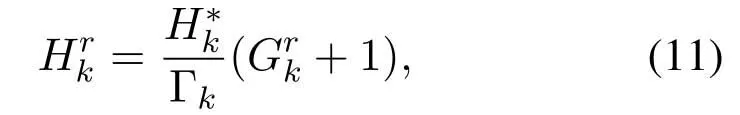
3.2 Ungerboeck M-BCJR Algorithm with CS
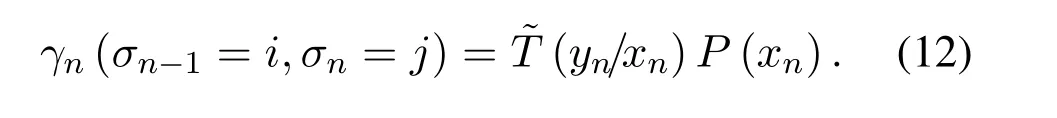

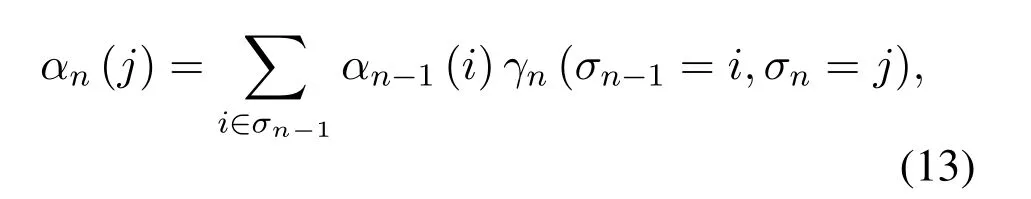
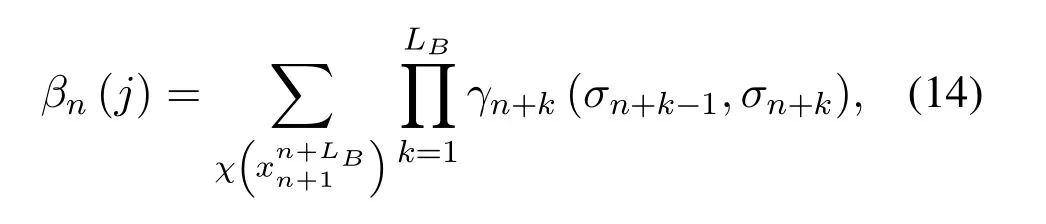

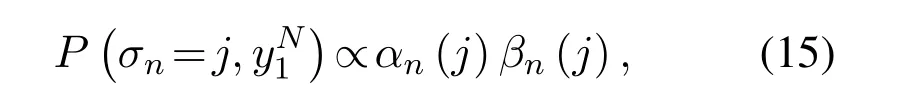
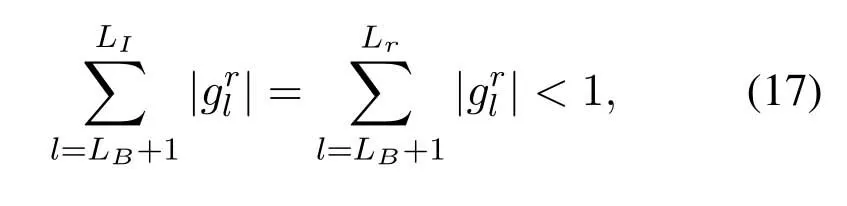
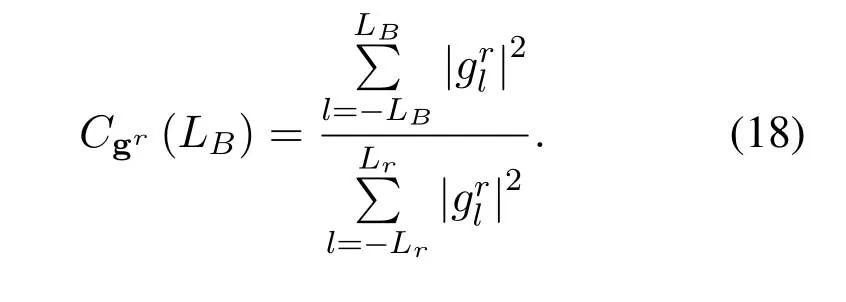
IV.CS OPTIMIZATION BASED ON IR CRITERION
4.1 IR Criterion
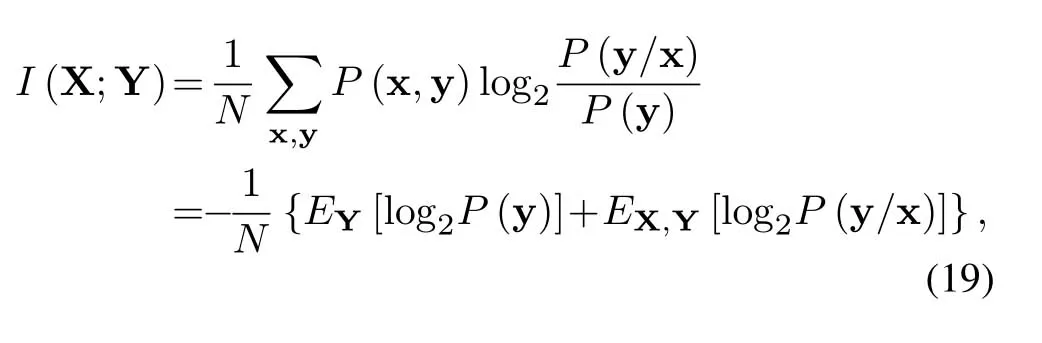
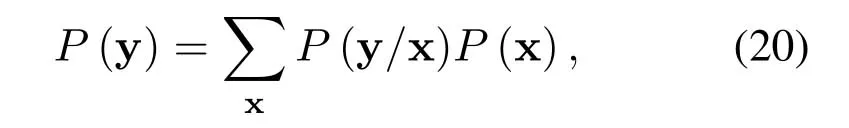
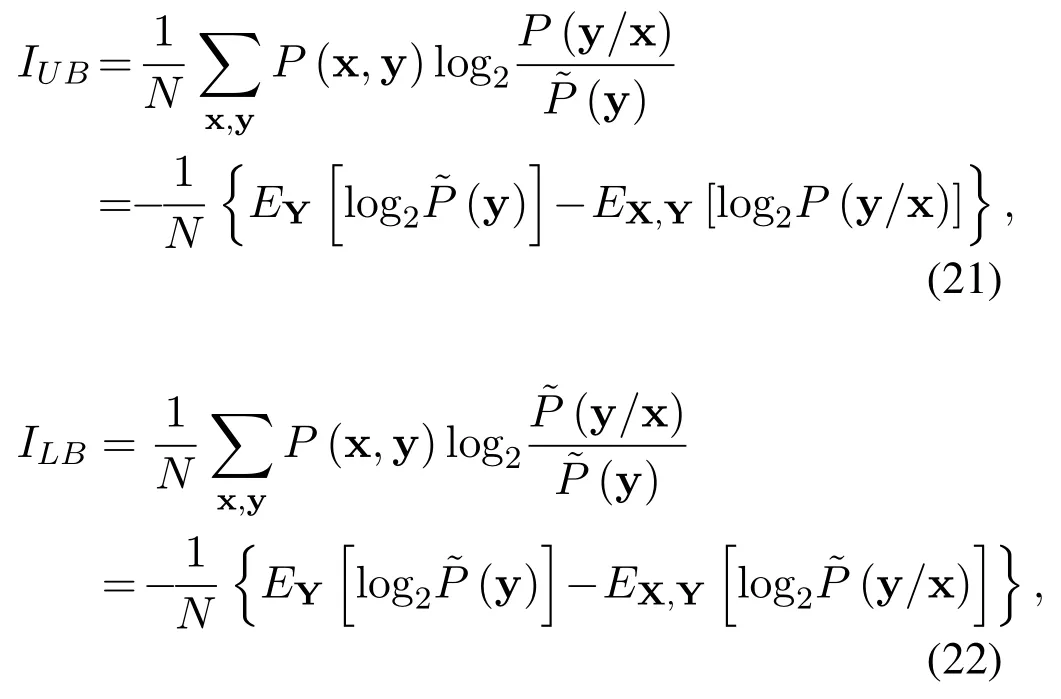
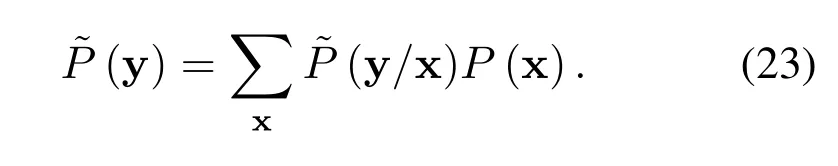
4.2 CS Optimization Based on IR Criterion
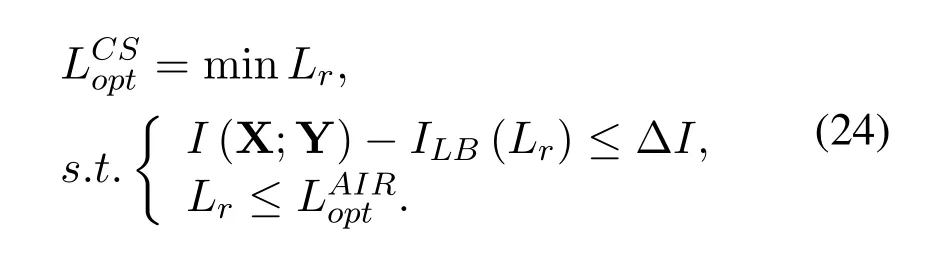
V.RESULTS
5.1 Case TPR=0.5

5.2 Case TPR=0.35
VI.CONCLUSION
- China Communications的其它文章
- Precoder Design and Impulsive Noise Mitigation Scheme for Industrial Wireless Communications
- Shortest Link Scheduling in Wireless Networks with Oblivious Power Control
- A Proactive Selection Method for Dynamic Access Points Grouping in User-centric UDN
- Energy-Efficient Power Allocation for IoT Devices in CR-NOMA Networks
- A New Solution Based on Optimal Link-State Routing for Named Data MANET
- NOMA-Based UAV Communications for Maritime Coverage Enhancement

