Program Error Mitigation in MLC NAND Flash Memory with Soft Decision Decoders

Zequn Fang,Zheng Ma,*,Xiaohu Tang,Yue Xiao,Youhua Tang

1 School of Information Science and Technology,Southwest Jiaotong University,Chengdu 610031,China

2 National Engineering Laboratory for integrated traffic data application technology,Southwest Jiaotong University,Chengdu 610031,China

Abstract:Benefiting from strong decoding capabilities,soft-decision decoding has been used to replace hard-decision decoding in various communication systems,and NAND flash memory systems are no exception.However,soft-decision decoding relies heavily on accurate soft information.Owing to the incremental step pulse programming (ISPP),program errors(PEs)in multi-level cell(MLC)NAND flash memory have different characteristics compared to other types of errors,which is very difficult to obtain such accurate soft information.Therefore,the characteristics of the log-likelihood ratio(LLR)of PEs are investigated first in this paper.Accordingly,a PE-aware statistical method is proposed to determine the usage of PE mitigation schemes.In order to reduce the PE estimating workload of the controller,an adaptive blind clipping(ABC) scheme is proposed subsequently to approximate the PEs contaminated LLR with different decoding trials.Finally,simulation results demonstrate that(1)the proposed PE-aware statistical method is effective in practice,and(2)ABC scheme is able to provide satisfactory bit error rate (BER) and frame error rate(FER)performance in a penalty of negligible increasing of decoding latency.

Keywords:program errors;soft-decision decoder;NAND flash memory;clipping approximation

I.INTRODUCTION

NAND flash memory has upgraded digital products due to the higher write and read speed,compared with conventional storage medium,e.g.,magnetic tapes and disks [1,2].Utilizing the physical feature of the transistor,data is recorded as charges in NAND flash memory cells.When applying read reference voltages(RRVs)on the control gates to turn on transistors,the corresponding sensed threshold voltages(TVs),whose values are affected by the amounts of charges,represent the stored data.In the early age of NAND flash memory,single-level cell (SLC) was employed to store 1 bit data in one cell.As the development of scaling technology,multi-level cells became domination in the modern NAND flash memory,which enlarges the storage capacity.Since multi-level cells can be divided into different varieties based on the different storage density(bits/cell),the NAND flash that containing 2 bits per cell is referred to multi-level cell(MLC) while the cells that representing 3 bits and 4 bits are denoted as triple-level cell (TLC) and quadlevel cell(QLC)respectively[3–5].

Nevertheless,the amount of stored charges in cells is not constant and can be changed by many effects,e.g.,program/erase cycles,data retention and read disturbs,which may result in overcharge or charge leakage.From a statistical perspective,the density distributions of TVs thus could be deformed and shifted.In the existing work[3,6–8],these effects were characterized by observing the variation of the distributions.Owing to the shortened distances between adjacent cells,multi-level cell NAND flash may suffer much more distortion than SLC NAND flash.

In order to protect the data from interference in multi-level cells NAND flash memory,many schemes have been proposed in the literature [4,8–12].As one of the basic operations on NAND flash memory,the programming process triggers charges injection into the floating gate by applying a high voltage on the control gate of the transistor.Nonetheless,larger programming voltage may increase programming interference due to cell-to-cell coupling.An alternative way,incremental step pulse programming(ISPP)is employed in current multi-level cell NAND flash memory [3,9,13,14].In ISPP,cells are first programmed to bepartially programmed stateswhich are calledpartially programmed cells.These partially programmed cells continue to be programmed by small step voltages until the cells reach the final target states and becomefully programmed cells.Constrained by the maximum programming voltage,the step voltage noise is more obvious as the step pulse voltages are smaller [4,14].In order to simplify the analysis and get better illumination,we only discuss MLC in this article,but it is straightforward to generate the proposed schemes to other high-order density cells such as TLC and QLC[15].

Error control coding(ECC)is also an effective solution for protecting data integrity.In the early stage of NAND flash memory,hard-decision decoding(HDD)codes,e.g.,Bose–Chaudhuri–Hocquenghem (BCH)codes,are good enough for error correction [4,16].But as multi-level cell NAND flash memory demands better data protection capability,the more powerful soft-decision decoding (SDD) codes,e.g.,lowdensity-parity-check (LDPC) codes with soft decoding,have been widely employed [4,16–21].Unlike the hard decision,SDD needs soft information which is usually expressed as log-likelihood ratio (LLR)[16].In order to obtain accurate LLR,it is inevitable to perform density estimation of TVs[4,22–24].For simplicity,the mixture models are usually chosen to describe the NAND channel,in which each state has an individual PDF and all the PDFs are summed in accordance with mixing probabilities.

Many works,e.g.,[4,22–24],have tried to fit the mixture models to the data perfectly and perform an optimized SDD to get the best decoding performance.However,errors that occur in partially programmed cells may be programmed into unexpected final states afterward,which is not in line with the naive mixture model assumption.As in references [4,9,25],this kind of errors is referred to asprogram error(PE).In 2016,the experimental results in[25]demonstrate the influence of PEs.Moreover,the vulnerabilities in MLC NAND flash memory programming were first investigated in[9].It proposed pass-through voltage optimization to reduce the raw bit error rate(RBER).However,when SDD is considered,LLR may be misidentified and result in poor decoding performance with the existences of PEs.

As far as the authors know,how the PEs affect LLR has not been addressed in previous work,which may prevent the potential of SDD from being fully exploited[17,18,20].Since the estimation of the exact density distribution for PEs cannot always be guaranteed in storage devices,we focus on investigating what measures can be used to obtain more accurate soft information,when PEs are existed.The contributions of this paper can be summarized as follows:

• We analyze the PEs contaminated LLR when the conventional mixture models are employed.Clipping approximation is proposed to approximate the LLR with PEs.

• An analytical PE-aware statistical method is proposed based on the LLR clipping approximation.Combined with read-retry mechanism,such a method can be performed without extra storage requirements.

• An adaptive blind clipping(ABC)scheme is proposed to approximate the PEs contaminated LLR without the knowledge of PEs’PDF.This scheme can track the optimal clipping value adaptively and provide near-optimal LLR to the soft decoders.

This paper is organized as follows.Section II gives preliminaries on programming and reading in MLC.The corresponding system model is established and PDF estimation is introduced subsequently.In Section III,PEs contaminated LLR is analyzed and approximated by PDF estimation.A PE-aware statistical method is proposed in Section IV and a blind LLR approximation method(ABC)is proposed in Section V.In Section VI,the simulation results are given.Finally,concluding remarks are made in Section VII.

II.PRELIMINARIES

In order to alleviate the interference,ISPP,which applies several smaller step voltages to program cells from the erased states to the final target states,is employed in multi-level cells programming.PEs,which occur in the partially programmed cells during ISPP procedure,may have large magnitudes of LLR and result in the degradation of decoding performance if the memory channel is not modeled appropriately.In MLC,ISPP is also recognized astwo-step programmingfor that the least significant bit (LSB) and the most significant bit (MSB) are programmed in two separated steps.

2.1 Two-step Programming

The PDFs of TVs in cells duringtwo-step programmingis sketched in Figure1.The management of the flash translation layer (FTL) in NAND flash ensures that all the cells experience almost the same wearing and tearing level [4,26].As a result,all the cells at different stages follow similar PDF.

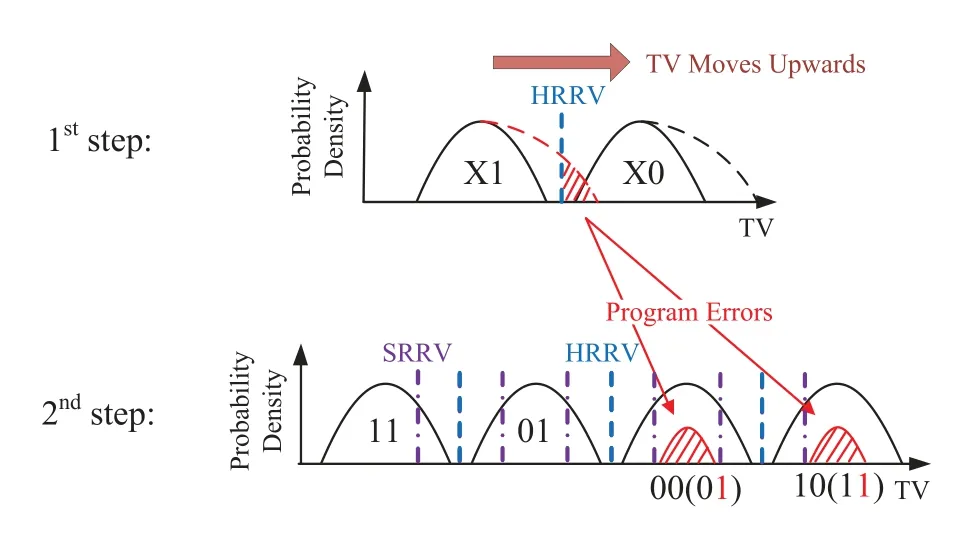
Figure1.The two-step ISPP in MLC.

As Figure1 shows,one MLC symbol consists of one LSB and one MSB.In one programming cycle,they are programmed in different steps.As shown by the upper part of the figure,LSB is first partially programmed to the temporary state (“X1” or “X0”) and the cell becomes the partially programmed cell.Subsequently,the data in the partially programmed cell is read and stored in an LSB buffer.Finally,combining the LSB from LSB buffer and MSB from the controller,the symbol is fully programmed to the target state (“11”,“01”,“00” or “10”) as the lower part of Figure1 shows.The cell with a fully programmed symbol is referred asa fully programmed cell.

At the early use stage of storage products,the channel is good and few errors occur.Unfortunately,partially-programmed cells are more vulnerable than fully-programmed cells as[9,12]indicated.The cellto-cell interference caused by the adjacent programming and reading raises the voltages of the temporary states.Consequently,interference can affect LSBs in temporary states seriously and asymmetrically[9,12].Due to the TV’s upwards movement,data shifting from temporary state“X”to“X0”is much more likely to occur than to the opposite direction.If the TVs of “X1” cross the hard-decision read reference voltage(HRRV)in the first programming step,these LSBs will be decided incorrectly in LSB buffering and reading stages.Moreover,because ECC is integrated into the controller,such LSB errors in the first programming stage cannot be corrected and would be turned into PEs in the fully-programmed cells[9],which are implied by the shadow areas in the state“00”and“10”in Figure1.

2.2 Reading and Recovery

Data reading directly affects the ability of data recovery in NAND flash memory.Without measuring the voltages directly,data are obtained by comparisons between RRVs and TVs of the fully-programmed cells and different numbers of comparisons can cause different levels of reading latency.In order to get a compromise in latency and performance,different levels of accuracy of read information can be dynamically selected[4].

When the HDDs are employed,only comparisons between HRRVs and TVs are required.On the contrast,if SDDs are invoked when better decoding performance is demanded,fully-programmed cells will be applied by several soft-decision read reference voltages (SRRVs),which are expressed by the dash-dot lines in the lower part of Figure1.For the purpose of providing soft information for the SDDs,LLR is required to be calculated according to the sensed TVs.In practice,the probability of a cell’s TV is obtained by integrating PDFs of “1” and “0” between two adjacent SRRVs,so the corresponding LLR is discrete.A controller could choose a proper reading level to achieve satisfactory decoding performance[4,27,28].Assuming an infinite number of SRRVs are used,LLR for each data can be represented in continuous PDF[24,27,29]as(1).

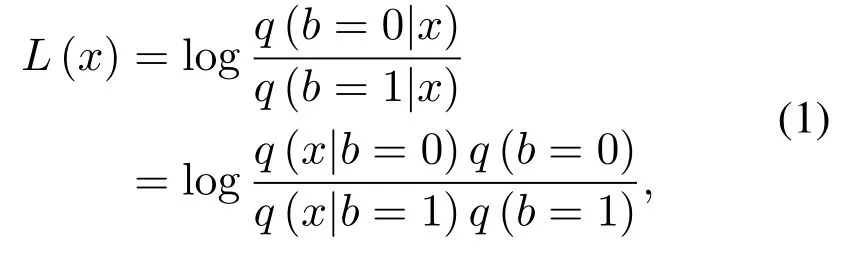
wherebis the programmed data andxis the TV representing for the reading voltage.q(x|b=0) andq(x|b=1) are the likelihood functions.If bit “0”and“1”are equiprobable,LLR can be simplified as

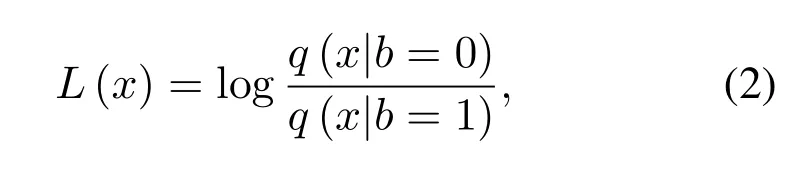
which is widely used in the most of the published literature[4,16–21,24,27].

2.3 System Model

For easy illustration,the noise in NAND flash memory channel is assumed as additive noise [3,4].In MLC programming,since the second programming step is processed on the basis of the reading results of the first programming step,PEs occur when the first step reading results are mis-decided.

In the first step,LSBs are expected to be programmed to the target TV,vd.However,noise blurs the distinction between bit ”0” and bit ”1”.The TVs present bell-shaped distribution (e.g.Gaussian distribution).Thus the voltage read from a cell after first programming step is expressed as

wheretdis a random variable that represents additive noise.The subscriptd ∈{1,2}and stands for the distribution index of state ”X1” and state ”X0” respectively.

In the second programming step,the PDF of the final state is denoted asgk,where the subscriptk ∈{1,2,3,4}and it is the distribution index of each final target state,one-to-one from left to right.According to the state of programmed LSB and unprogrammed MSB,the symbol that consists of LSB and MSB is programmed with an incremental step pulse.The TV after this step is modeled as

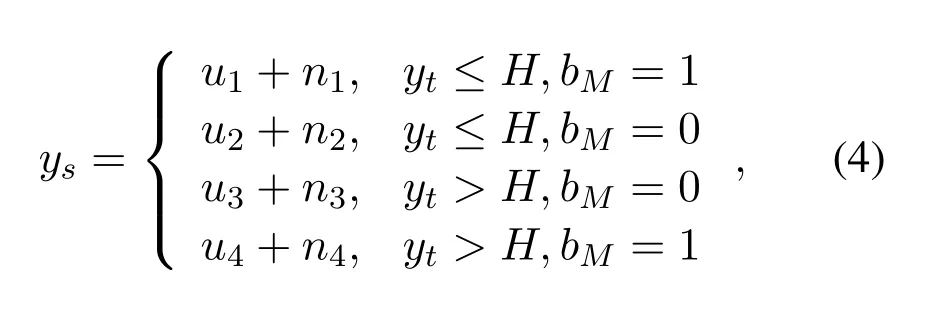
whereukis the mean TV of the final state,nkis a random number represents additive noise,His the HRRV of temporary state andbMis the MSB.PE occurs during the comparison betweenytandH.If an LSB is decided incorrectly,the symbol would be programmed into an unexpected state.

2.4 PDF Estimation and PEs

Since soft information is closely related to the PDF of voltages,PDF estimation for final states is vital for SDD.

In order to compensate for the deformation and shifts of the PDF of TVs,read-retrymechanism has been implemented in modern flash memories [4,18,22].This mechanism allows the NAND flash memory controller to obtain more accurate decoding information to improve the decoding performance if necessary.Normally,a 4-component mixture model (4-MM) is utilized as the PDF of TVs [17,20,22].The 4-MM has 4 bell-shaped PDFs (e.g.,Gaussian distribution)of corresponding target states in MLC memory and can be described as a linear superposition of all the components:

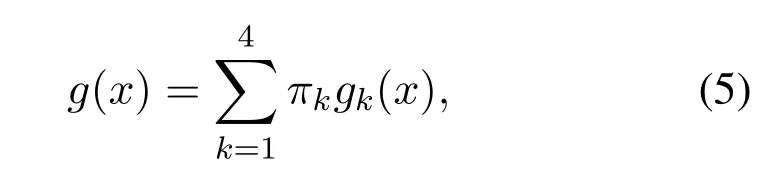
whereπkis the mixing probability that implies the probability of each state and the subscriptk ∈{1,2,3,4}representing the index of each state.When one-shot programming is utilized,each symbol is directly programmed to a target state and this mixture model is reasonable.However,when the ISPP is applied,the distribution of the TVs will change subtly because of PEs.From Figure1,it is clear that considering the mis-programmed PEs,the 2 PDF components on the right may no longer simply represent their respective symbols,but are composed of a mixture of two symbols.

There is a hypothesis that the different symbols in the 4 target states are of equal probability,i.e.,πk=0.25,when the above 4-MM is utilized for PDF estimation[4,24].But the appearance of PEs changes the probabilities.For the sake of estimating PDF with PEs,the known pseudo-random data were programmed into the cells of the same wearing-level in[9]and [25],then the corresponding TVs were read after certain amounts of interference.With the experimental results,vulnerabilities in MLC NAND flash memory programming have been thoroughly investigated in [9]and non-ECC mitigations,e.g.,passthrough voltage optimization,have been proposed to reduce the number of PEs.But regardless of the accelerated cell wearing problem caused by the extra program/erase (P/E) and read processes,a more obvious drawback of this approach is that large amount of extra erased storage space should be reserved,which can not be guaranteed on a full-load storage device.Therefore,an online flash channel modeling scheme is further proposed in[25],which stored the parameters of the channel models based on the experimental tests of P/E and assumes that the NAND flash memory products can obtain online accurate channel model at different stages.However,online testing is too resourcecostly to be used in practice.

In order to mitigate PEs without the sophisticated estimation,we prove that the conventional 4-MM is not applicable for PEs contaminated LLR and propose to use simple LLR approximation to modify the imperfect LLR in the next section.

III.LLR CLIPPING

In this section,we first define the“perfect”4-MM estimationwith PEs,and then propose an LLR approximation method.

3.1 LLR of‘‘Perfect”4-MM Estimation

With read-retry mechanism,the accuracy of the PDF of the 4-MM can be optimized through data fitting(Section 2.4).However,because of the premise that the 4 states represent different symbols individually,the PDF of the PEs cannot be estimated in practice.

Without considering PEs,the voltage corresponding each symbol has its individual PDF,i.e.,voltage of symbol “11” is assumed to followg1(x),“01” is assumed to followg2(x),“00” is assumed to followg3(x) and “10” is assumed to followg4(x).Such a scenario could not be consistent when PEs appeared,that is,the mixing probabilityπk /=0.25.In most works like [4,20,21,23,24,27],LLRs of LSB and MSB are usually derived as(6)and(7)based on(2).

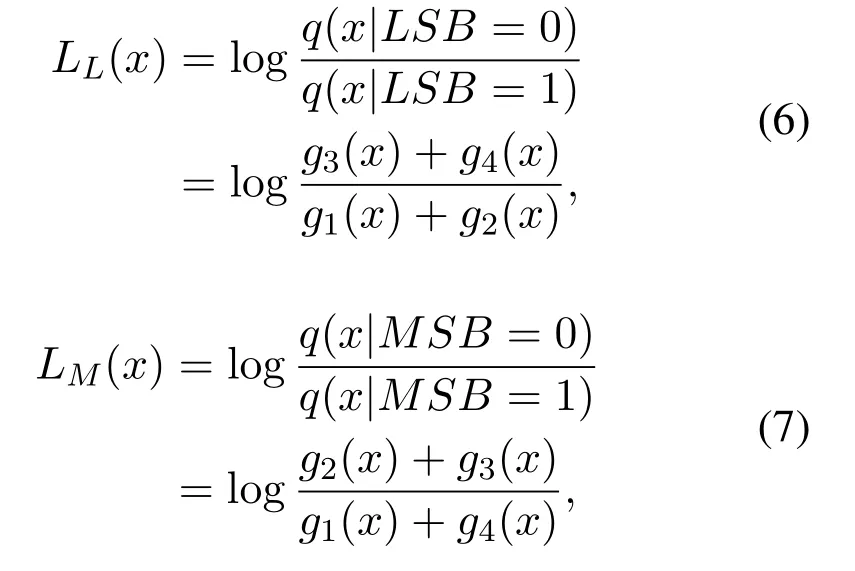
whereLL(x) is the LLR of LSB andLM(x) is the LLR of MSB.In the following sections,the 4-MM is considered to be “perfectly” estimated as long as the likelihood functions are accurately estimated.The LLR calculation based on this“perfectly”4-MM estimated is denoted as the conventional LLR calculation.

3.2 Approximation of PEs Contaminated LLR

Because PDF is always positive and bell-shaped,the magnitudes of LLR can an be very large in (6) and(7).Without identifying PEs,the conventional LLR calculation is not accurate as Theorem 1 shows,which may degrade the decoding performance.

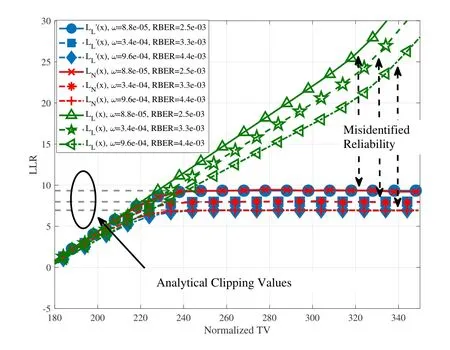
Figure2.LLR comparison between LL(x),LN(x),L＇L(x)and La(x).

Theorem 1.Given q(yt >H|LSB=1)=ω,LLR of LSB page bit is strictly smaller than −logω.

Proof.For the sake of simplicity,g1(x)+g2(x)is abbreviated asg12(x),g3(x) +g4(x) is abbreviated asg34(x) andLSBis denoted asBin the equations.Based on the fitting conclusion in [25],PDF of LLR with PEs followsg34(x) whenω>0.From the perspective of probability,we now have

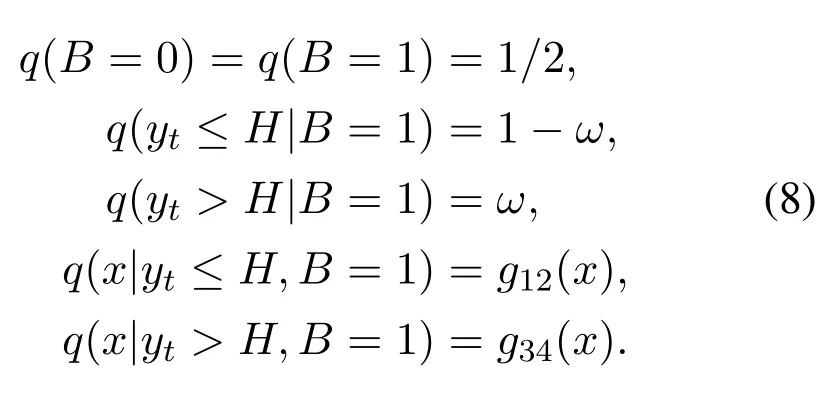
Utilizing the laws of total probability and conditional probability,when LSB “1” is stored,the likelihood function of the received data can be derived as

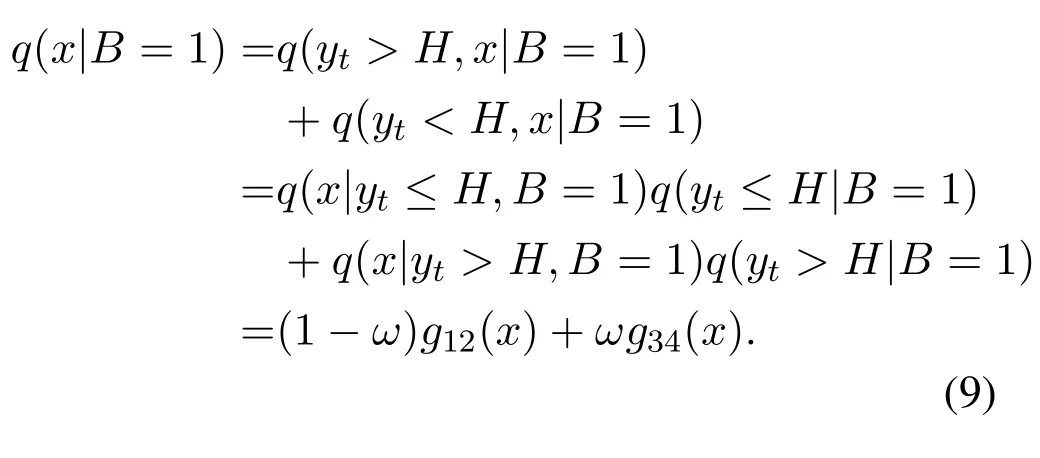
Because of the occurrence of PEs,q(x|B=1) is quite different from that without considering PEs.On the other hand,accounting for the asymmetric voltage offset,there are almost no PEs in LSB“0”s.The likelihood is expressed as(10),when LSB“0”is stored.

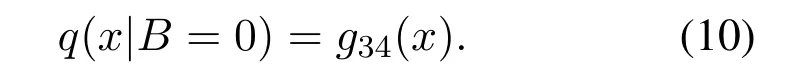
As a result,the PEs contaminated LLR of LSB can be calculated as

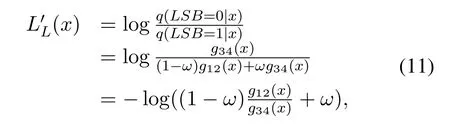
Since 0≤ω<<1[25],we have

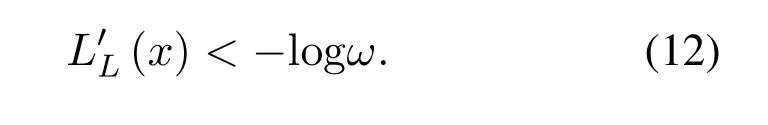
Therefore,LLR of LSB page bit is strictly smaller than−logω.

Comparing (6) and (12),it can be seen that when the PEs exist,the LLR of LSB can not be infinitely large,but always less than−logω.Thus,a simple but effective approximation of PEs contaminated LLR is proposed in(13),which is a clipping operation on the conventional LLR.In hardware implementation,this approximation can be achieved by a limiter.

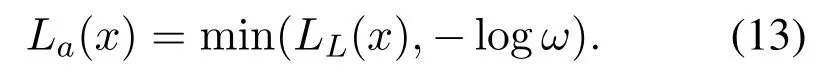
In order to show the effectiveness of LLR approximation in(13),different approaches to calculate LLR are compared in Figure2.To be consistent with[3,4,8,9,25],the horizontal axisnormalized TVis employed in Figure2 where the nominal value of passthrough voltage is equal to 512 in the normalized scale and 0 represents ground(GND).Non-parametric estimation is utilized to draw accurate base LLR functions with known pseudo-random data like [9]and [25],where the corresponding LLR is denoted asLN(x).It can be observed thatLL(x)misidentifies the reliability largely on the right side,whileLL＇(x),LN(x),and the analytical clipping values match well with each other.

As for MSBs,the PEs cannot affect the conventional LLR calculation as Theorem 2 indicates.

Theorem 2.LLR of MSB page bit can still be calculated by using(7),when PEs exist.

Proof.As illustrated before,PEs occur in the first programming step in ISPP.Even if an LSB is incorrectly decided and the symbol is programmed into an unexpected state,it is still a correct state for MSB.Therefore,g1(x)+g4(x)still represents the likelihood functionq(x|MSB=1)andg2(x)+g3(x)representsq(x|MSB=0).With PEs,the LLR calculation for MSB page bit is coincide with(7).

From the above analysis,it can be seen that,the LLR value may be higher than it should be when PEs exist.

IV.PROGRAM ERROR AWARE STATISTICAL METHOD

In order to correctly clip the LLR affected by LEs,we propose an approach to be aware of PEs with predetermined probabilities.

4.1 Statistics of PEs

Under the assumption that all the states have equal probability,the RRVs can be optimized to distinguish“1”and“0”with the aid of decoding results in[30,31].Meanwhile,the sampling-based method in [6]optimized the RRVs by finding a voltage value that results in the best decoding result.Such approaches normally find the optimal RRVs by using the hard decision bits directly or checksum results.However,relying on hard decision information is not sufficient to mitigate PEs.

Theoretically,the probability of PEs can be estimated by subtracting the probability of other types of errors from total probability of errors.Thus,clipping approximation (13) or the accurate calculation (11)with the calculatedωcan result in accurate LLR.However,unlike the PDF estimation of 4-MM,the error data that can be used by PEs statistics estimation is much fewer[25].

Accordingly,when PE is the dominating type of errors,based on the analysis in Section 3.2,we can have

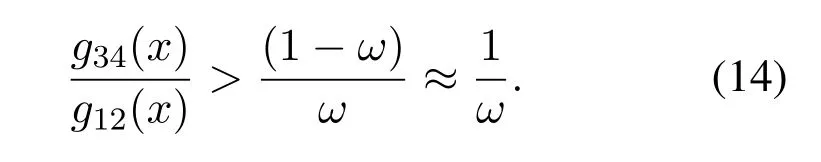
Applying the logarithm on(14),we have

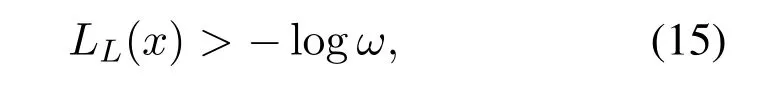
which is highly relative with(13).

4.2 The Proposed PE-aware Statistical Method

Considering that the value ofωkeeps increasing in the lifetime of NAND flash memory [25]until that PEs start to affect the decoding performance,the threshold isω∗.This value ofω∗can be provided by the manufacturers.In the same stage of wear-leveling,the controller receives the input and output of the SDD.The difference can be measured by XORing the hard decision input and hard output with each other.Simultaneously,the locations of the LLRs that larger than−logω∗can also be located by the controller.Thus,the number of errors caused by PEs can be determined.With sufficient data,the probability of PEs,Pω,can be obtained in the region that satisfiesLL(x)>−logω∗.If it is approximately equal or larger than the preset probability of PEs in that region,Pω∗,a mitigation scheme,e.g.,the following ABC scheme,will be invoked and a newω∗is updated for the next level of PE occurrence probability.

?

V.ADAPTIVE BLIND LLR APPROXIMATION

In this section,an adaptive blind clipping (ABC)scheme is proposed to approximate the optimal LLR without introducing the overhead of accurate PDF estimation.

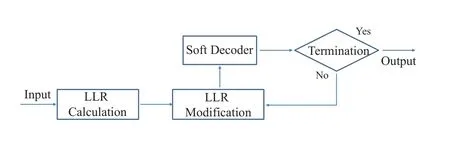
Figure3.Diagram of ABC algorithm.

The ABC scheme consists of at most 3 decoding trials and the diagram is shown in Figure3.Based on the conventional soft decoding process,a procedure of LLR modification is added in this scheme.The core idea of this scheme is to apply different candidate clipping values to approach the true LLRs in case of the existence of PEs.

?

The pseudo code of the scheme is shown in Algorithm 2.Given a clipping vector W that consists of(W1,W2,W3),it is initialized as(W∗,s1×W∗,s2×W∗),whereW∗is a target clipping value that may be set as−logω∗.After receiving the input TV vector x,the LLR is calculated with(6)firstly to getLL(x).According to Theorem 1,LLR values with PEs should be strictly smaller than−logω.However,LL(x) might go infinite when PEs occur.Therefore,based on(13),the LLR modification module clipsLL(x)withWjas follows

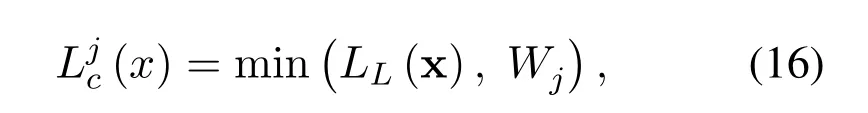
wherejis the index ofj-th decoding trial andWjis an approximate clipping value.

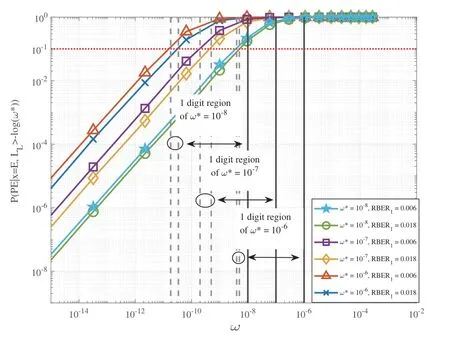
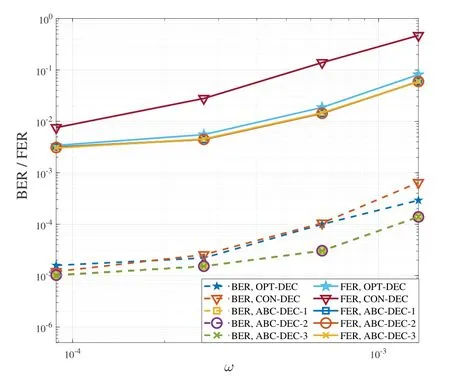
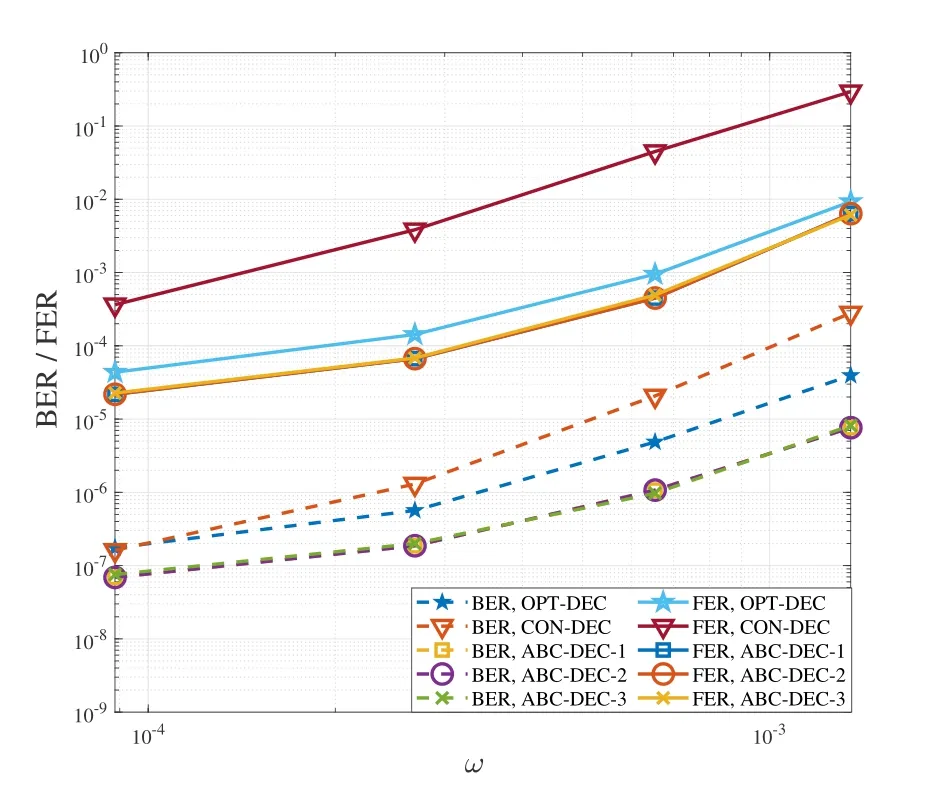
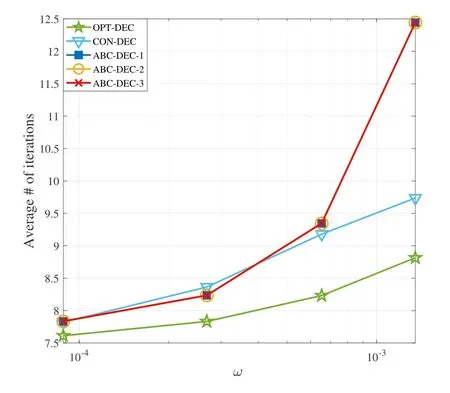
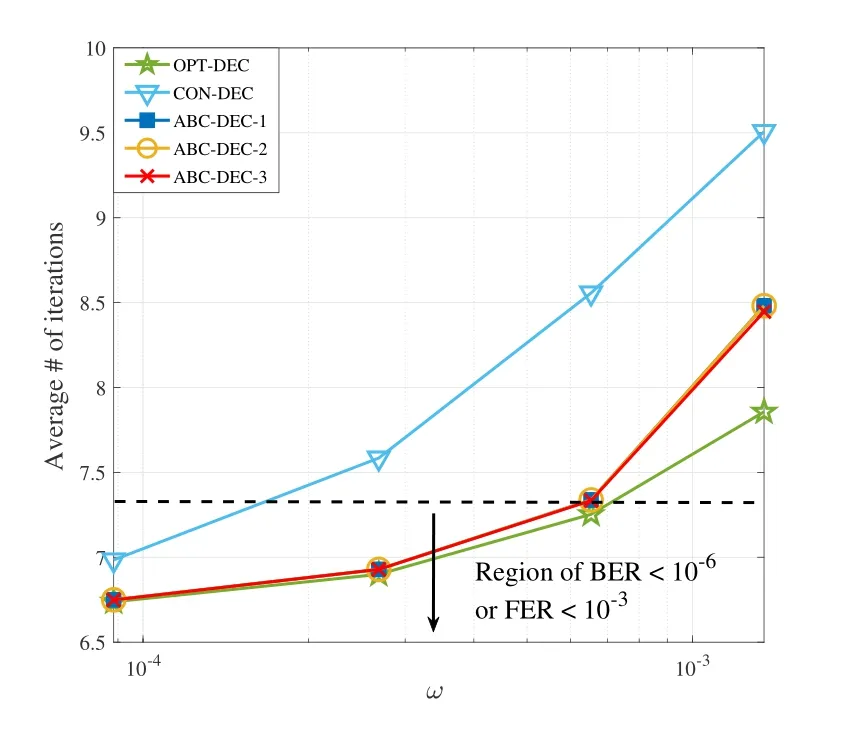
Initially,we set the clipping valueW1as close to−logωas possible.When the first decoding trial fails,the two more decoding trials would be invoked.If thej-th decoding trial successes,Wjwill be considered as a better clipping value.In order to reduce the negative impact for LLR values without PEs,a smaller step size is chosen to updateW1,i.e.,W1=(W1+Wj)/2.Thus,along with the decoded output,a new clipping value vector W is generated as(W1,s1× W1,s2× W1),wheres1is the downward step factor that 0

VI.SIMULATION RESULTS

In this section,the simulation results of PE-aware statistical method are provided firstly with different values ofω∗.Subsequently,the decoding performance comparisons,namely,BER/FER comparison and decoding latency comparison,are given.The simulations are performed with equivalent pulse-amplitude modulation(PAM)and additive white Gaussian noise as[3,4]suggested.

6.1 Simulations of the PE-aware Statistical Method

As discussed in Section IV,the validity of data counting is important for PEs statistics.In order to ensure that there will be enough PEs in the total counted errors,conditional probability,P(PE|x=E,LL(x)>−log(ω∗)),is utilized in this subsection.The value of the conditional probability corresponds to the proportion of PEs in the counted errors.

The conditional probabilityP(PE|x=E,LL(x)>−log(ω∗)) with differentω∗is depicted in Figure4.It can be seen clearly that the values of conditional probability are quite small whenωis far smaller thanω∗.With certain number of total errors,the proportion occupied by PEs are negligible.Asωapproachesω∗,the values of conditional probability keep increasing close to 1,especially whenω ≥ω∗.This means that the closerωapproachesω∗,the more accurateωis.Moreover,if only the accuracy of 1 significant digit is considered,the statistical results ofωis several orders of magnitude smaller thanω∗,which is also reliable.

6.2 Simulations of the ABC Scheme

The ABC scheme tries to track the optimal clipping value to obtain accurate LLR.In the simulations of ABC scheme,a (9118,8225) LDPC code is utilized,which is the Code 3 used in[27].Meanwhile,the normalized min-sum (NMS) decoding algorithm is employed and the maximum number of decoding iterations is set as 10.The BER/FER comparisons are conducted with RBER1=0.015 and RBER1=0.013,where RBER1is the RBER of other types of errors other than PEs.We denote the conventional method of calculating LLR and decoding [4,16–21,24,27]as CON-DEC.Simultaneously,the decoder with LLR in(11)is denoted as OPT-DEC and the decoders with ABC scheme are denoted as ABC-DEC.In order to investigate the effects ofW∗,three ABC-DECs usingW∗=−log 10−15,−log 10−10,and−log 10−5are expressed as ABC-DEC-1,ABC-DEC-2,and ABCDEC-3 respectively.

Figure4.Conditional probability of PE when given ω∗=10−8,10−7 and 10−6.

Figure5.BER performance comparison,RBER1=0.015.

Figure6.BER performance comparison,RBER1=0.013.

Figure7.Decoding latency comparison,RBER1=0.015.

As can be seen in Figure5,there is almost no difference in the BER/FER performance of ABC-DEC-1,ABC-DEC-2,and ABC-DEC-3.Simultaneously,they have the lowest BER/FER comparing with other two methods.In other words,the ABC-DECs have the best BER/FER performance.It is interesting that the ABC-DECs even perform better than OPT-DEC.Furthermore,with lowerω,there is an intersection between the BER curve of OPT-DEC and CON-DEC.And the FER performance of OPT-DEC is better than CON-DEC.Such a phenomenon can also be spotted in Figure6.Due to theclipping,the LLR values of the correct bits are clipped together with that of the PEs.Considering the cases that PEs with large LLRs are the main contributor to decoding failures,the clipping of the PEs shall improve the decoding performance.However,if the decoding failure is caused by other types of errors without large LLR,the clipping lead to performance loss.Therefore,although the FER performance of OPT-DEC is better than CON-DEC,the BER performance may be worse.On the other hand,the ABC scheme can provide adaptive clipping values and perform better than both schemes.

Figure8.Decoding latency comparison,RBER1=0.013.

In addition to the BER/FER decoding performance,another main concern is the decoding latency.In Figure8 and Figure7,the average numbers of LDPC decoding iterations are compared.It can be seen that OPT-DEC performs best whereas CON-DEC has the highest decoding latency.The decoding latency of ABC-DECs increase sharply when BER>10−5.On the other hand,it is slightly higher than OPTDEC when BER<10−6.More specifically,there is only less than 0.02 more iterations/codeword for ABCDEC scheme.Since the storage products usually work in an even lower BER/FER region [4],the increasing latency of ABC-DEC scheme is actually negligible when compared with OPT-DEC.

VII.CONCLUSION

In this paper,the problem of PEs is described and analyzed firstly in MLC NAND flash memory.With the simple but effective clipping approximation,the characteristics of PEs contaminated LLR are summarized.Accordingly,a PE-aware statistical method is proposed.Subsequently,an ABC scheme is introduced,which could approximate the PEs contaminated LLR adaptively without statistical estimation.Finally,simulation results are provided to verify the feasibility of the PE-aware statistical method and ABC scheme.Compared with the decoders using conventional LLR calculation,the ABC scheme even have superior performance at the cost of negligible increasing of decoding latency.

ACKNOWLEDGEMENT

This work was supported by Key Project of Sichuan Province(no.2017SZYZF0002)and Marie Curie Fellowship(no.796426).