A Topological Evolution Model Based on the Attraction of the Motif Vertex
Xing Li,Shuxin Liu,*,Yuhang Zhu,Yingle Li
1 PLA Strategic Support Force Information Engineering University,Zhengzhou 450001,Henan Province,China
2 National Digital Switching System Engineering and Technological R&D Center,Zhengzhou 450002,Henan Province,China
Abstract:As a fundamental problem in the field of the network science,the study of topological evolution model is of great significance for revealing the inherent dynamics and mechanisms of complex network evolution.In order to study the influence of different scales of preferential attachment on topological evolution,a topological evolution model based on the attraction of the motif vertex is proposed.From the perspective of network motif,this model proposes the concept of attraction of the motif vertex based on the degree of the motif,quantifies the influence of local structure on the node preferential attachment,and performs the preferential selection of the new link based on the Local World model.The simulation experiments show that the model has the small world characteristic apparently,and the clustering coefficient varies with the scale of the local world.The degree distribution of the model changes from power-law distribution to exponential distribution with the change of parameters.In some cases,the piecewise power-law distribution is presented.In addition,the proposed model can present a network with different matching patterns as the parameters change.
Keywords:complex network;topological evolution model;network motif
I.INTRODUCTION
As a research hotspot in the field of network science,the topological evolution model is a fundamental problem in the complex network research.The studying of the evolution mechanism of complex networks has important guiding significance for constructing realistic networks that conform to macroscopic statistical laws[1–3].
Typical topological evolution models of complex networks mainly include regular network model [4],ER random graph network model[5],WS small world network model [6],NW small world network model[7]and scale-free network (BA) model [8].Li et al.[9]found that the preferential attachment mechanism only exists in the local scope in the research of the world trade network and the Internet,and proposed a Local World (LW) evolution model.Saramaki et al.[10]proposed a method for constructing a scale-free network based on random walks,which produced the same result as the BA model.Jiang et al.[11]proposed a topological evolution model by constructing a local world through three attachment policies during random walks:“random selection”,“poverty alleviation”and“favoring the rich”.Zhu et al.[12]proposed a coupled evolution model of scale-free network based on the principle of competitive exclusion.Cui et al.[13]studied the mechanism of the common-neighbordriven network evolution from the local structure of the network.Li.et al.[14]proposed a coevolving network evolution model based on the preferential triadic closure for social media networks.
In recent years,with the deep research of complex networks,researchers have developed various network evolution models,e.g.,neighborhood evolution model[15],accelerating growth model[16],physical position neighborhood evolution model[17],mixing evolution model for bidirectional microblog user networks[18],community structure-based topological evolution model[19],the co-evolution model based on social network evolving and opinion migration [20],the dynamic evolution model based on weighted localworld [21],the network evolution model for supply chain[22]and so on.
Most current researches on evolution models focus on the scale of nodes,and there is a lack of attention to the topological relationship around the nodes.More and more empirical studies have shown that preferential attachment is not only a preference for individuals,but rather a more comprehensive choice of individuals,and organizational structures to which they belong[23–25].For example,in an online social network,the addition of new users and the establishment of new connections are comprehensive choices for the relationship between the current user and its surrounding friends.Li et al.[26]proposed a weighted multi-localworld network evolution model by studying the dense links between nodes in a local world,the sparse links between nodes from different local worlds,and the different importance between intra-local-world links and inter-local-world links.Liu et al.[27]proposed a new social network evolution model considering the influence of node hobbies on connection preferences.As a ubiquitous topology structure in complex networks,the motif is essentially the classifying and clustering on nodes in the social organization form [28].Network motifs can be seen as an”expansion”of network nodes.The preference for node degree and the degreerelated preferential attachment are the most common patterns in the topological evolution model,while current models lack the perspective from the network motif on the network evolution.Barab´asi et al.[29]studied on the motif and concluded that the network motif plays a more important role in the specific topology evolution.Costa et al.[30]also pointed out that the network motif is an important structure in the process of topology evolution.Therefore,it is of great significance to establish a topological evolution model based on the network motif to explore the influence of different connectivity relationships of the equivalent network motif on the topological evolution,and promote the research of preference of individuals for community selection and the differences of the preferences in different networks.
Based on the analysis above,in this paper,we propose a topological evolution model based on the attraction of network motif vertex.From the perspective of the scale of the network motif,the model proposes the attraction of the motif vertex based on the degree of motif vertex,quantifies the extent to which the preferential attachment is affected by the local structure,and performs the preferential selection of the attraction of the motif vertex based on the Local World model.The simulation experiments show that the model has the small world characteristic,and the clustering coefficient varies with the size of the local world.The degree distribution of the model changes from power-law distribution to exponential distribution with the change of parameters.In some cases,a piecewise power-law distribution is presented.Moreover,the model can present different matching pattern networks with different proportions of the motif vertex.
II.THE PROPOSED TOPOLOGICAL EVOLUTION MODEL
In this section,we first introduce the basic concept of network motif.Then we give the definition of the motif vertex degree by referring to the concept of network node degree,and describes the quantitative calculation method of the influence of network motif on network nodes.Finally,we introduce the proposed topological evolution model based on the attraction of the motif vertex.
2.1 Basic Concept of Network Motif
Network motifs[31]and communities[32]are important community structures in complex networks.The size of a community is relatively large,and there are fewer connections between different communities.As one of the basic topologies that constitute the network,the motif is small in size and is a structure between nodes and communities.The motif is more suitable to study the influence of organizational structure on topology evolution.Generally,the motif is composed of a few nodes,and the evolution process between motifs is essentially the interconnection within the structure of the community[33].
Milo et al.[28]first proposed the concept of network motif in 2002.They found that motifs in different networks are different in the research of the World Wide Web,the food chain network and the neural network.In general,the probability of a particular network motif appearing in a real network is greater than the expected value that appears in a random network.The network motif can be defined as a subgraph that satisfies the following conditions:
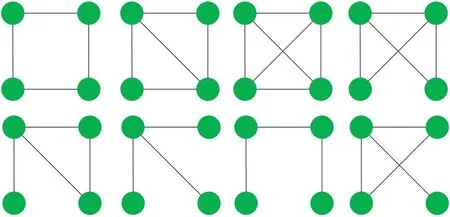
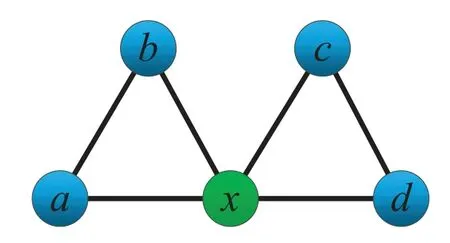
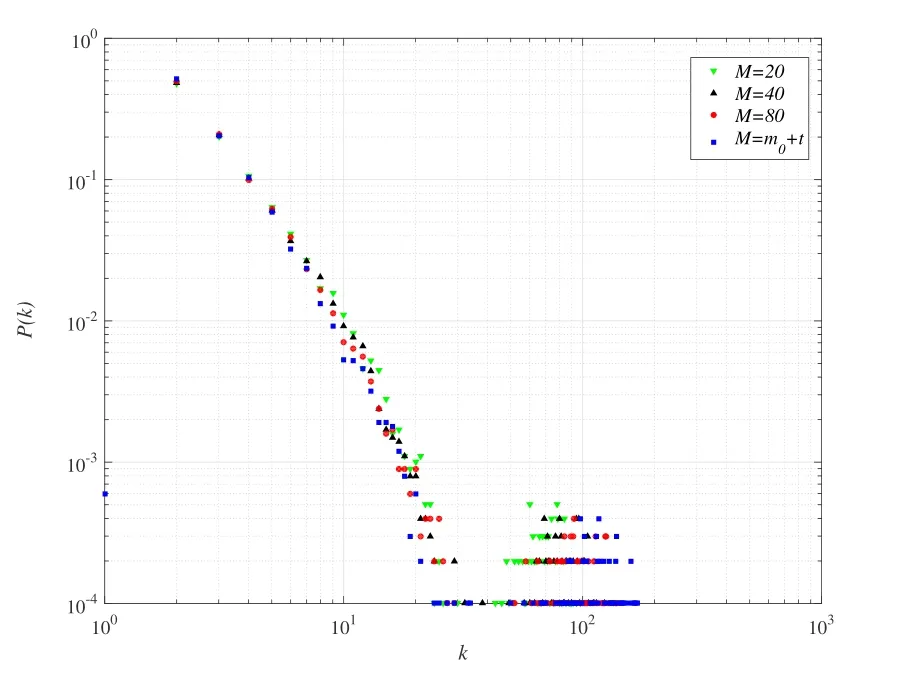
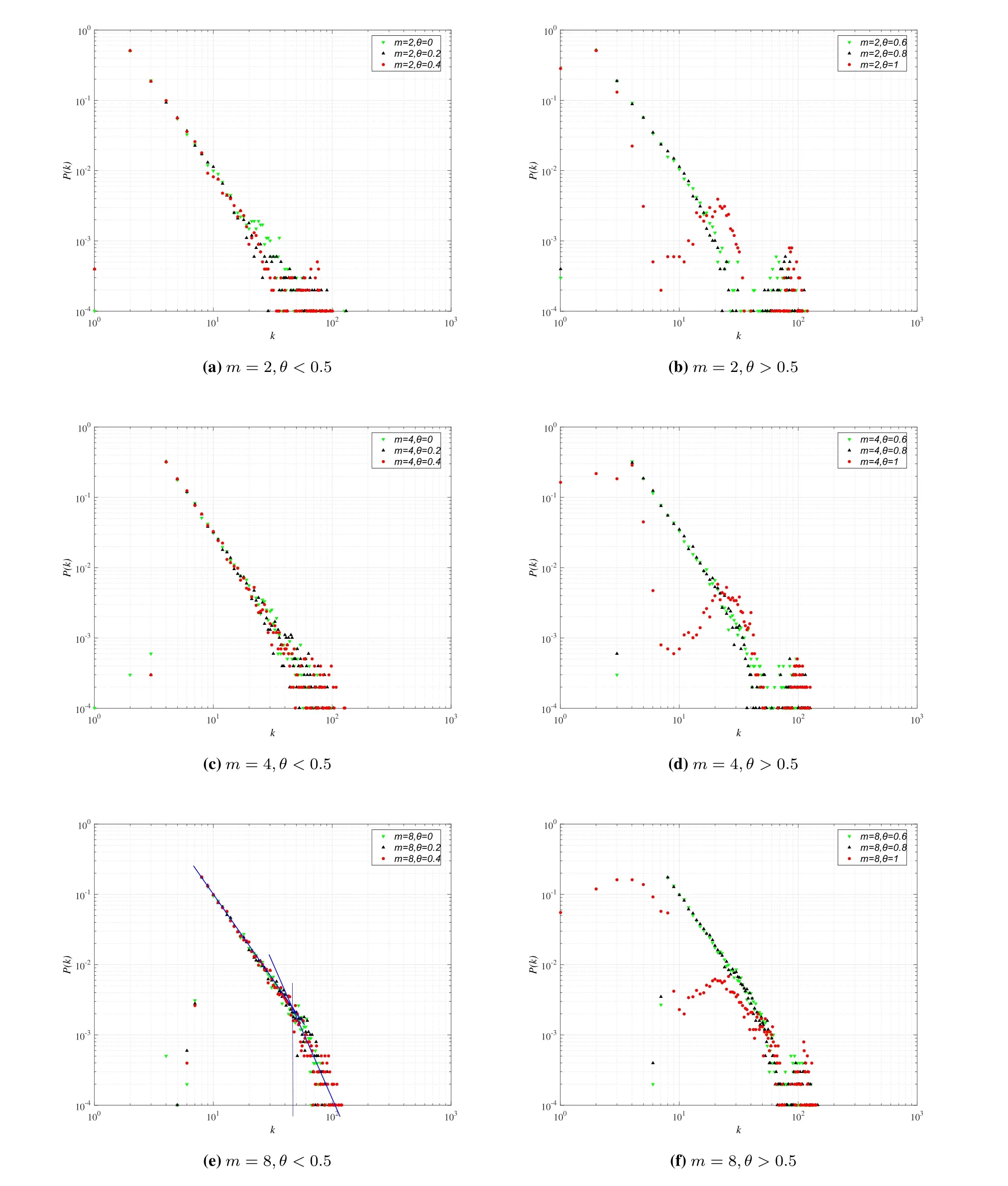
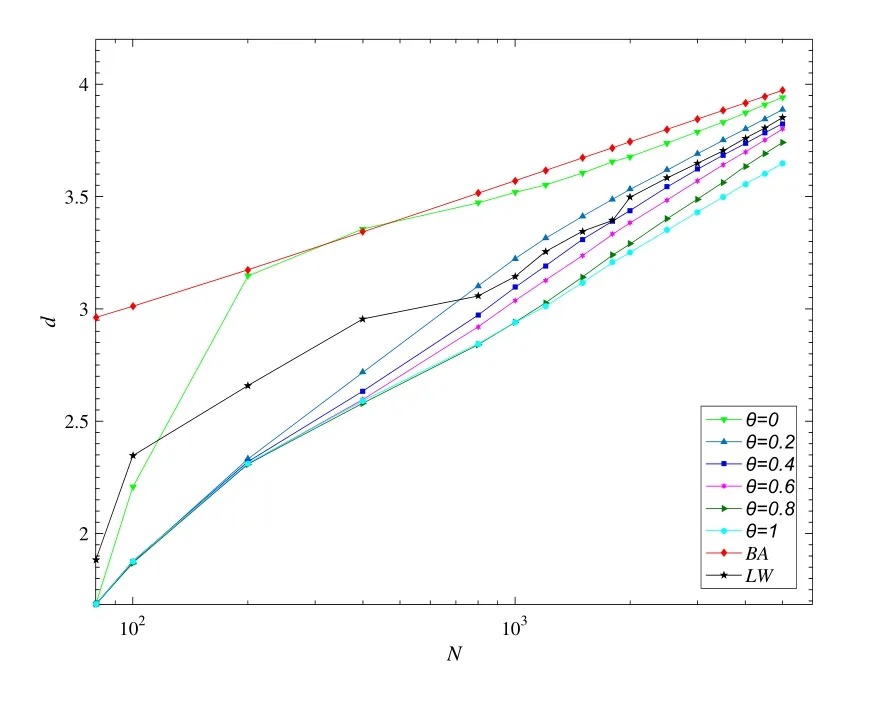
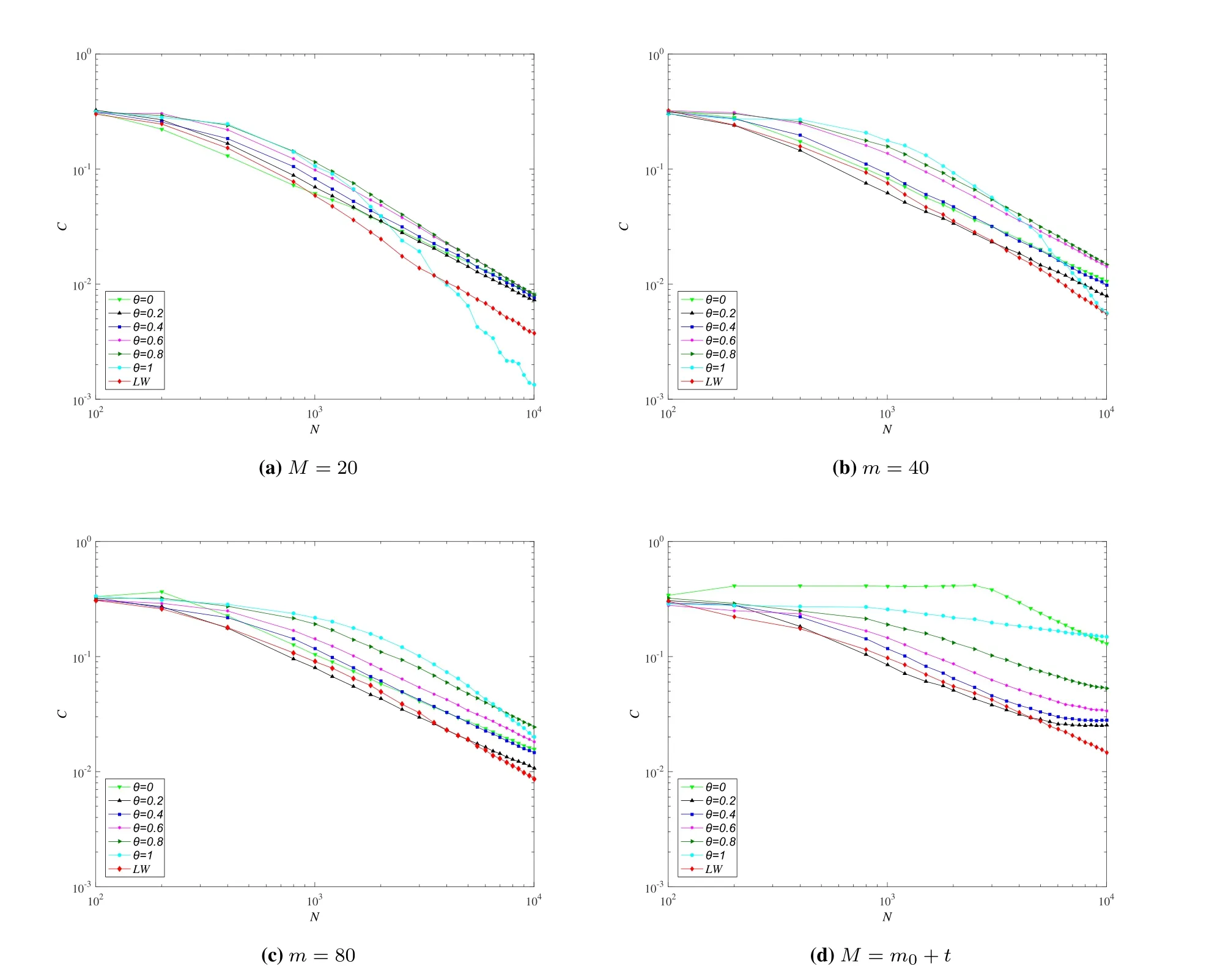
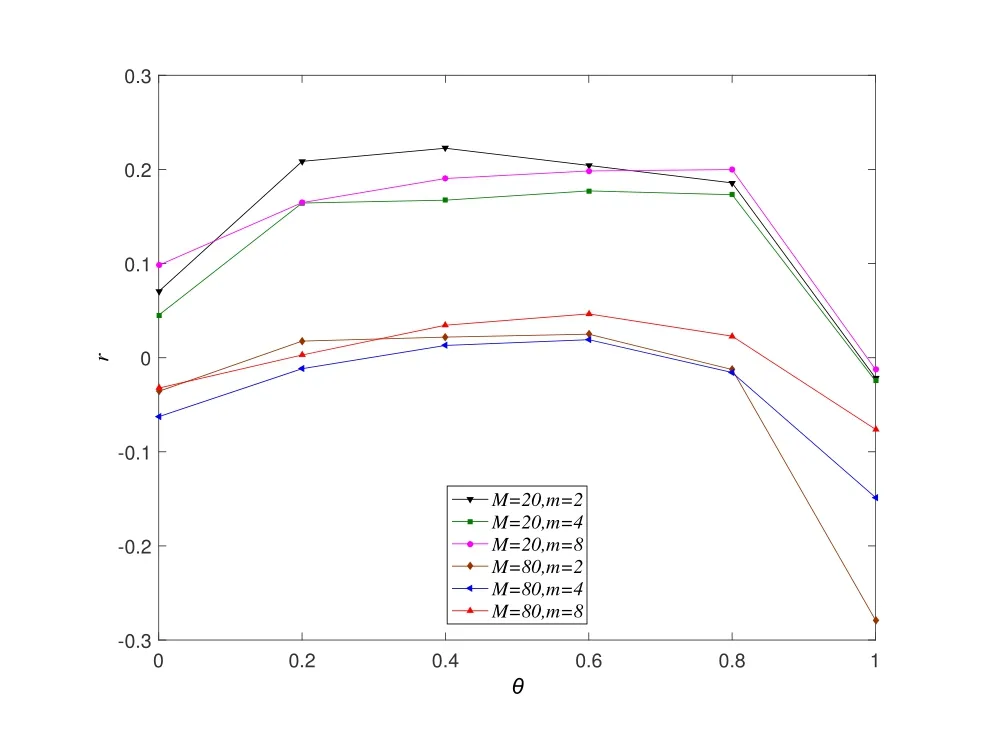
• In the actual networkGand the corresponding random networkG',the probability that the number of occurrencesT(s ∈G') of the subgraphsin the random network is greater than the number of occurrencesT(s ∈G) in the actual network is less than a set thresholdPa,which can be expressed asP{T(s ∈G')>T(s ∈G)} • In the actual network,the number of occurrences of the subgraph is greater than the set lower limitTa,i.e.,T(s ∈G)>Ta; • The number of occurrences of the current subgraph in the actual network is significantly higher than the number of times it appears in the random network. In the real world,network motifs are generally composed of several nodes,and the most common network motifs are composed of three or four nodes.For an undirected and unweighted network,the third-order network motif includes two different connection relationships,as shown in Figure1.The fourth-order motif includes eight different connection relationships,as shown in Figure2. Figure1.Schematic diagram of the third-order network motif. For a single network node,the network motif it belongs to will inevitably have a certain impact on it.This section studies how to quantify the impact of network motifs on nodes.For the particular case like second-order motif (i.e.,the motif with only two nodes),the node degree can indicate the number of the second-order motifs that the current node contains,and can also quantify the influence of the network motifs on the node to some extent.Strictly speaking,the second-order motif is not a network motif,because the probability of its existence in the actual network and the random network is similar.For the multi-order motifs,we refer to the concept of network node degree and give the definition of network motif vertex degree. Definition 1.Network motif vertex degree:Given an undirected and unweighted network G(V,E),where V denotes the set of nodes and E denotes the set of edges.For a node vi and a motif Mj (e.g.,the fully connected triangular motif in Figure1),the network motif vertex degree of the node vi is defined as the number of motif Mj with vi as the vertex,and is denoted as Figure2.Schematic diagram of the fourth-order network motif. Just as the node degree can represent the importance of a node in the network,the network motif vertex degree describes the importance of a node and its communityMjin the network from the perspective of the network motif.However,there may be multiple forms of connected subgraphs for the same-order motifs (e.g.,there are eight different same-order motifs in Figure2),and different connected subgraphs have different contributions to the influence of the current node.Therefore,in order to analyze the impact of different forms of motifs with the same number of nodes on the current node,the concept of attraction of network motif vertex is proposed as follows: Definition 2.Attraction of network motif vertex:For any node vi in an undirected and unweighted network G(V,E),the network motif vertex attraction MFi of the node vi is defined as the weighted sum of the vertexdegrees of each motif with vi as the vertex,which is expressed as where M1,M2,M3,...,Mn are different forms of motifs with the same number of nodes,and n is the number of motifs.E.g.,for the fourth-order motif,n=8.And θ is the weight of different motif vertex degrees,which can adjust its influence on the network motif vertex attraction,wherein θ1+θ2+...+θn=1. Figure3 shows the calculation diagram of the attraction of network motif vertex.The nodexhas four neighbouring nodes{a,b,c,d},and both the node pairs (a,b) and (c,d) have connected edges.Taking the third-order motif as an example,M1represents the fully connected triangular motif,andM2represents the semi-triangular motif.It can be seen that in Figure3),there are two fully connected triangular motifs withxas the vertex,which are (x,a,b) and (x,c,d).Then,the motif vertex degreeof the nodexis 2.Similarly,there are four semi-triangular motifs withxas the vertex,which are (x,a,c),(x,a,d),(x,b,c) and (x,b,d).Therefore,the motif vertex degreeof the nodexis 4.Then,according to Eq.(1),the motif vertex attraction of the nodexisMFx=θ×2+(1−θ)×4=4−2θ,whereθis the weight of the motif vertex degree Figure3.Schematic diagram of calculating the attraction of network motif vertex. The network motif has a certain attraction to the new nodes,while the network motifs with different numbers of nodes can be characterized by the same attractionMF.Based on the attraction of the network motif vertex,the topological evolution model is proposed as follows: Step 1:Initial network:at the momentt=0,the initial network consists ofm0nodes and randomly connectede0links,and the network is fully connected; Step 2:Local world:randomly selectMnodes in the network to form a local world; Step 3:Growth:add one node andmnew links each time; Step 4:Preferential attachment according to the attraction of the motif vertex:the probability of establishing a connection between the new node and the existing nodeiis proportional to the attractionMFiof the motif vertex of the nodei.The specific probability is Step 5:Return to Step 2 until the network reaches the specified size. It can be seen that when the network motif is a second-order motif,the model degenerates into a Local World model.The focus of the model proposed in this paper is to explore the influence of the motif vertex on the topology evolution.However,if the model is applied to other topological evolution models,it still has practical significance. As the basic unit composed of complex networks,the third-order motifs can be regarded as important primitives in the evolution of complex networks from nodes to networks.Many studies[34,35]believe that third-order motifs can provide accurate local topology information,which is of great significance for network evolution analysis.Moreover,the third-order motifs contain only two different subgraphs,which is very convenient to analyse the impact of different connected subgraphs on the network evolution.Therefore,in order to analyse the macroscopic statistical results of the proposed topology model,we take the thirdorder motifs as examples for empirical analysis. In the third-order case,the Eq.(1)can be simplified as follows whereθis the adjustment parameter,M1denotes the fully connected triangular motif,andM2is the semitriangular motif,as shown in Figure1. The macroscopic statistics of a large number of realistic networks show that the node degree distribution of the real network is not a pure power-law distribution,and often presents different distribution forms,e.g.,power-law distribution,piecewise power-law distribution,and shifted power-law distribution.Meanwhile,the network has an obvious”small world”phenomenon and a higher clustering coefficient.In this section,we analyze the validity of the proposed model mainly from four perspectives:node degree distribution,small world characteristic [6],clustering coefficient[36],and degree correlation coefficient[37]. To analyze the node degree distribution of the proposed model,we first derive the model equation from the LW model.The mean field equation of the LW model is: Based on Eq.(4),for any nodei,the change of the model degree is: Substituting Eq.(3),the formula can be expressed as: The motif vertex degreeof the nodeiin the full triangle is: whereciis the clustering coefficient of the current nodei,which can reflect the probability of existence of links between neighbors of the current node,and denote the number of full triangles to some extent.However,the relationship between the half triangleand the node degree is diffciult to determine.It is necessary to consider not only the number of semitriangular motifs after excluding the full triangle,but also the number of motifs that are constructed by the current node and its surrounding nodes.The half triangle contains two aspects:taking the intermediate node as the vertex,or use any remaining node as the vertex.Therefore,the Eq.(6)is difficult to express only withki,so it is necessary to study the degree distribution through actual simulation. First,the influence of the local world sizeMon the degree distribution is discussed.Figure4 shows the influence of different local world sizes on the degree distribution of the proposed model underm=2 and different values of parameterθ.In Figure4a,θ=0 indicates that only the influence of the semi-triangular motif on the preferential attachment is considered.It can be seen that with the increase of the size of the local world,the degree distribution of the network is always maintained in the power-law distribution,and the power law index does not change much.As shown in Figure4b and Figure4c,whenθ=0.4,0.6,the degree distribution of the proposed model exhibits a near power-law distribution that develops toward the exponential distribution,but the size of the local world has less influence on the network degree distribution.When the local world is the entire network,it is more obviously biased towards the exponential distribution.It can be seen from Figure4d that whenθ=1,the size of the local world has a greater influence on the degree distribution of the network.WhenM=20,the degree distribution presents a near power-law distribution in the front section,breakpoint saturation in the middle,and a near power-law distribution in the back section.WhenM=40,80,the degree distribution presents a near power-law distribution with small variable saturation [38].When the local world is the entire network,the degree distribution presents a near power-law distribution with a slight exponential tendency.Moreover,as the size of the local world gradually increases,the position of the small variable saturation gradually moves forward.UntilM=m0+t,the small variable saturation disappears.Given that in most cases,the size of the local world has little effect on the degree distribution of the proposed model,the sizeMof the local world generally takes 20 in the subsequent analysis. Figure4.The influence of different local world sizes on the degree distribution of the proposed model under m=2 and different parameters θ. To illustrate that the proposed evolution model is more in line with the statistical characteristics of the degree distribution of the actual network,Figure5 shows the simulation results of the degree distribution of the LW model.It can be seen that when the local world is the entire network,the degree distribution of the LW model follows the power law distribution.And when the local world size is smaller than the network scale,the degree distribution tends to be exponential.As mentioned at the beginning of Section III,the degree distribution of real-world networks not only exhibits power-law distribution and near-power-law distribution,but also often exhibits piecewise power-law distribution and shifted power-law distribution.Compared with the LW model,the proposed model can generate more forms of degree distribution through parameter changes.Therefore,the proposed model can be suitable for studying the evolution mechanism of more kinds of networks. Figure5.The degree distribution of the Local World model with m=2. Next,we analyze the influence of the numbermof new links and the parameterθof the attraction of the motif vertex on the degree distribution of the proposed model.Figure6 shows the influence of differentθandmon the degree distribution.Figure6a gives the degree distribution whenm=2 andθ <0.5.It can be seen that whenθis small,the model conforms to the power-law distribution,and whenθ=0.4 its tail exhibits a slight exponential distribution tendency,indicating that the exponential tendency of the degree distribution has a greater relationship with the weight reduction of the semi-triangular motif.Figure6b shows the degree distribution whenm=2 andθ >0.5,and the model has an overall tendency to the exponential distribution.However,whenθdoes not reach 1,the exponential distribution tendency does not change significantly with the increase of the parameterθ,and the model still maintains a near power-law distribution.This shows that the increase ofθhas a limited influence on the tendency of the network exponential distribution,which is consistent with the macrostatistical law of the actual network.Meanwhile,whenθ=1,the degree distribution presents the form of near power-law distribution in the front section,single peak in the middle,and power-law in the back section.Figure6c and Figure6d show the variation of the degree distribution with the change ofθwhenm=4.Similar to Figure6a and Figure6b,the degree distribution conforms to a power-law distribution whenθ <0.5,and the tail has a slight exponential distribution tendency and presents a near power-law distribution whenθ >0.5.However,unlikem=2,the influence ofθon the exponential tendency of the power-law distribution becomes smaller and it does not exhibit an exponential tendency whenθ=0.4.Whenθ=1,the model presents a piecewise exponential distribution,which indicates that the preferential attachment of the full triangular motif has a greater impact on the degree distribution.Figure6e and Figure6f give the variation of the degree distribution with the change ofθwhenm=8.The difference from the above is that the degree distribution presents a distinct piecewise power-law distribution with different power index whenθ <0.5.This is in line with the actual network,such as the Nanjing University microblog network which is statistically analyzed by Wang et al.[39].Whenθ >0.5,the piecewise power-law phenomenon of the proposed model gradually disappears.However,whenθ=1,both the front and the back section of the degree distribution are in the form of an exponential distribution. In summary,the different number of linksmhas little effect on the power exponent of the network,but it will affect the influence of the parameterθon the network degree distribution.In general,the network exhibits a power law distribution to an exponential distribution(slight exponential distribution tendency)under different parameters.In some cases,a piecewise power-law distribution is presented,and in most cases,a near power-law distribution is presented.The proposed model presents a power-law distribution form when the local world is small,which shows that the comprehensive selection of network nodes and their organizational relationships is also an important mechanism for power-law distribution.The larger the vertex degree parameterθ,the more serious the exponent tendency of the model.However,as the number of linksmincreases,the tendency will be alleviated.Statistics show that many real networks conform to the near power law distribution between exponential and power-law distribution [38].When the local world is small,the proposed model generates a near power law distribution in most cases,which is consistent with most real networks.In addition,the model also presents the piecewise power-law distribution,which conforms to the statistical laws of some actual networks,and can also provide theoretical explanation for the formation of some specific networks. The small world characteristics of a complex network can be characterized by the average shortest path of the network.Figure7 shows the average shortest pathdof the proposed model with the change of the network node sizeNunder different parametersθ,whenM=20,m=4. It can be seen that compared with the BA model,the average shortest path of the proposed model is smaller,and it keeps in a smaller range as the size of the network node increases,indicating that the proposed model has more obvious small world characteristics.Moreover,with the parameterθincreases,the average shortest path of the proposed model is gradually reduced,indicating that the preferential attachment of the full triangle motif is more conducive to the formation of small world networks.In addition,compared with the LW model,when the parameterθis larger(such as greater than or equal to 0.4),the average shortest path of the proposed model is smaller than that of the LW model.On the one hand,this also shows that the preferential attachment of the full triangle motif can generate a small world network.On the other hand,it shows that the proposed model is more consistent with the small-world statistical characteristics of the real network than the LW model. Figure6.The influence of different parameters on the degree distribution of the proposed model. Figure7.The analysis of small world characteristics of the proposed model with different parameters. Figure8 shows the variation curve of the clustering coefficient with the number of network nodesNunder different local world sizes and different values ofθ.It can be seen from Figure8a that the clustering coefficient of the proposed model is generally maintained at a high level,and is generally higher thanO(N−1)with different network sizes.Except whenθ=1,the clustering coefficient appears to decrease rapidly when the network size is large.The difference of the clustering coefficient with different values ofθis not large,indicating that the ratio of the full triangular and semi-triangular motifs has little influence on the clustering coefficient when the local world is small.The results of Figure8b and Figure8c show that with the increase of the local world sizeM,the influence ofθon the clustering coefficient gradually increases,indicating that with the expansion of the node selection range,the influence of the ratio of full triangular or semi-triangular motifs on the network clustering is gradually increasing.Meanwhile,whenθis large (e.g.,θ=1),as the local world size increases,the network clustering coefficient gradually slows down the decreasing tendency as the network size increases.In general,the larger the parameterθ,the lager the clustering coefficient,indicating that the full triangular motif is more conducive to the improvement of network clustering.Figure8d shows the variation curve of the clustering coefficient with differentθwhenM=m0+t.When the nodes perform the preferential attachment according to the motif vertex attraction in the whole network,the overall clustering of the network is significantly higher than that of 20,40,and 80.Different from the above cases,the network clustering coefficient maintains a certain level under different parameters over time and does not decrease rapidly with time.Moreover,except for the case ofθ=0,as the adjustment parameterθincreases,the clustering coefficient of the network gradually increases,indicating that the preferential attachment of the full triangular motif is beneficial to improve the clustering of the network.On the other hand,it is revealed that networks with high clustering tend to select the full triangular motif (i.e.,a solid social small group)when performing preferential attachment. It is worth noting that,unlike Figure8a,Figure8b and Figure8c,whenθ=0 in Figure8d,the clustering coefficient of the network is the highest.The possible reason is that whenθ=0,the proposed model performs preferential attachment of the half triangle.At this time,if a new edge is selected in the global range,there is a high probability of forming a new full triangle,so the clustering of related nodes is increased with a certain probability.However,if a new edge is selected in the local range,there is a greater probability of forming a new half triangle,so the probability of increasing the clustering of related nodes is low. Compared with the LW model,it can be found that the clustering coefficient of the proposed model is higher than that of the LW model in almost all cases,which shows that the proposed model is more consistent with the macroscopic statistical characteristics of the actual network than the LW model.In short,the clustering coefficient of the proposed model decreases slowly and the overall value is much higher thanO(N−1)when the local world is small.Moreover,as the local world size increases,the clustering coefficient no longer continues to decline and can remain at a higher level.In addition,the adjustment parameterθof the motif vertex attraction can adjust the clustering coefficient of the network.In most cases,the largerθis,the higher of the network clustering generated by the model is.The larger the local world is,the larger the adjustable range is. Figure8.The variation curve of the clustering coefficient with network size under different local world sizes and parameters θ(m=4). Figure9.The variation curve of the degree correlation coefficient of the proposed model with the change of the parameter θ. Figure9 plots the variation curve of the degree correlation coefficient of the model with the change of parameterθ.The overall degree correlation coefficient of the model has a value range of (-0.3,0.2),which is consistent with the statistics of the real networks.WhenM=20,the degree correlation coefficient of the model changes within the range (-0.05,0.25),i.e.,the nodes with a large degree tend to attach the nodes with a large degree.It can also be seen from the figurethat with the change of parameterθ,the majority correlation coefficients will fluctuate around 0.2.Whenθapproaches 1,the degree correlation coefficient will drop sharply to -0.05 or so,indicating that when the full triangular motif is preferred,its heterogeneous characteristics are most prominent.Moreover,different number of linksmhas a slight influence on the degree correlation coefficient.The fewer the number of links,the higher the degree correlation coefficient.WhenM=80,the degree correlation coefficient of the model changes within the range (-0.3,0.05),indicating that the nodes with a large degree are more likely to attach nodes with a small degree.It can be seen from the figurethat with the change of parameterθ,the majority correlation coefficients will fluctuate around 0.Whenθapproaches 1,the degree correlation coefficient will drop sharply to about-0.3.Similar to the results ofM=20,when the full triangular motif is preferred,the heterogeneous characteristics of the network are most prominent.In addition,the different number of linksmhas a slight influence on the degree correlation coefficient,and the larger the number of links,the higher the overall degree correlation coefficient. In general,the proposed model can generate networks with different matching patterns from homogeneous to heterogeneous.When the local world is small,the network is more inclined to be homogeneous.Many real-world networks,such as interpersonal networks and online social networks,are all positively correlated,and the model to some extent shows that the generation of these homogeneous networks is closely related to the small selection range of individuals during the preferential attachment.The networks related to“people”are more inclined to the perceptual attachment,thus its attachment range is small.When the size of the local world increases,the network is more inclined to be heterogeneous.Some technical cooperation networks and biological networks all exhibit negative correlations,which is related to the large selection range of individuals during the preferential attachment in these networks.When the parameterθis close to 1,that is to say,when the full triangular motif is preferentially attached,the heterogeneous characteristics are obvious. This paper studies the preferential attachment problem from the perspective of the network motif.Firstly,the definition of the motif vertex attraction is given to quantify the degree of attraction of the nodes and their surrounding organizational relationships to other nodes.Meanwhile,a topological evolution model based on the motif vertex attraction is proposed.Based on the Local World model,the model takes the network motif vertex attraction as the preferential attachment criterion.The simulation results show that the model has obvious small world and scale-free characteristics,the degree distribution changes from powerlaw distribution to exponential distribution,and some cases show piecewise power-law distribution.The network clustering coefficient of the proposed model is large and can change with the adjustment parameter.The degree correlation coefficient of the proposed model varies from (-0.3,0.2) and varies with the adjustment parameter.In general,the proposed topological evolution model is consistent with the macro statistics of the real networks.In the future,we will study the effects of different forms of motifs with different number of nodes on topological evolution and how to select the appropriate motifs according to the characteristics of the network. ACKNOWLEDGEMENT This work is supported by the National Natural Science Foundation of China(No.61803384).We gratefully acknowledge anonymous reviewers who read drafts and made many helpful suggestions.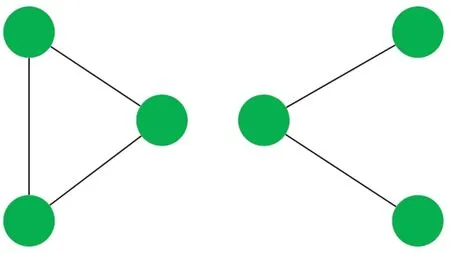
2.2 Attraction of Network Motif Vertex
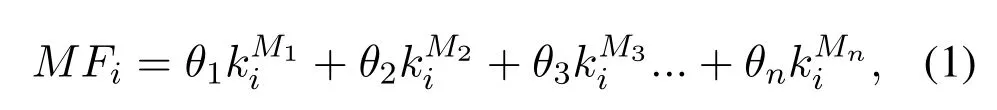
2.3 The Proposed Model
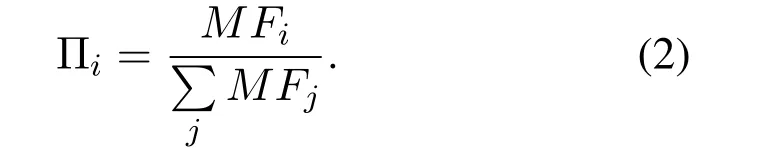
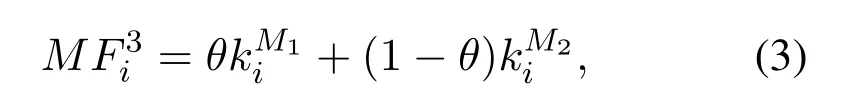
III.EMPIRICAL ANALYSIS OF MODEL VALIDITY
3.1 Node Degree Distribution
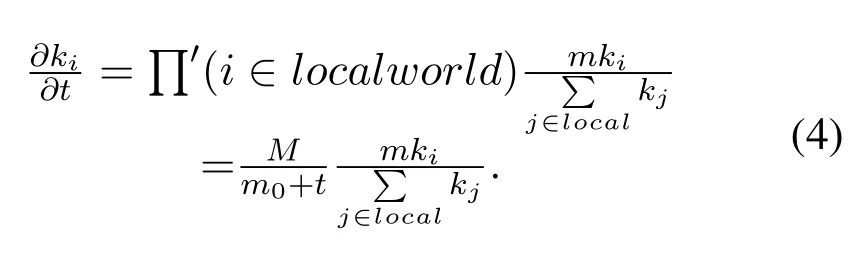
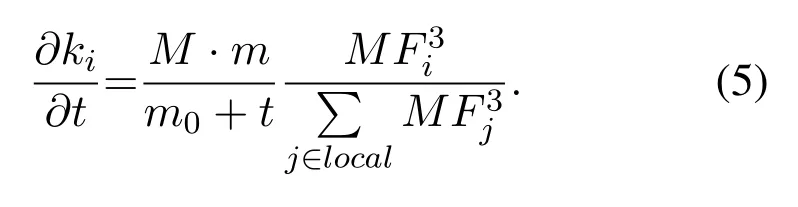

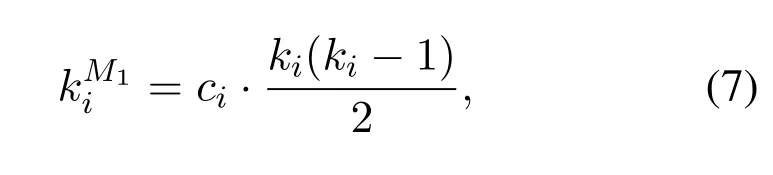

3.2 Small World Characteristic
3.3 Clustering Coefficient
3.4 Degree Correlation Coefficient
IV.CONCLUSION
- China Communications的其它文章
- Precoder Design and Impulsive Noise Mitigation Scheme for Industrial Wireless Communications
- Shortest Link Scheduling in Wireless Networks with Oblivious Power Control
- A Proactive Selection Method for Dynamic Access Points Grouping in User-centric UDN
- Energy-Efficient Power Allocation for IoT Devices in CR-NOMA Networks
- A New Solution Based on Optimal Link-State Routing for Named Data MANET
- NOMA-Based UAV Communications for Maritime Coverage Enhancement

