例谈函数极限的求法

陈小燕

(海南省海口市琼台师范学院 571100)

一、求极限的常用方法

1.无穷小量及其性质

性质1 有限个无穷小的和也是无穷小

性质2 有界函数与无穷小的乘积是无穷小.

性质3 常数与无穷小的乘积是无穷小.

性质4 有限个无穷小的乘积也是无穷小.

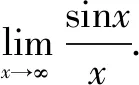
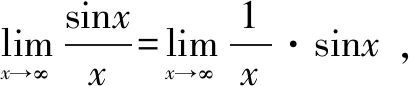
2.利用等价无穷小

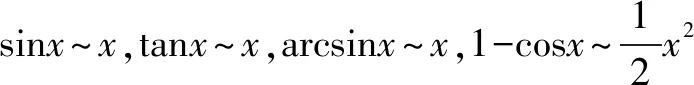
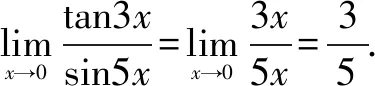
3.极限的运算法则

如果limf(x)=A,,limg(x)=B,那么

(1)lim[f(x)±g(x)]=limf(x)±limg(x)=A±B;

(2)lim[f(x)·g(x)]=limf(x)·limg(x)=A·B;

说明：只有两个函数都有极限时才能用运算法则，特别是用商的法则时分母的极限不能是零.

解x→1时,分子、分母的极限都是零,不能直接用法则.

但分子和分母有公因子x-1，先约去为零的因子x-1,然后再求极限.

4.利用夹逼准则

准则：如果

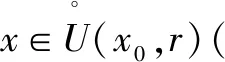
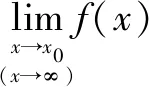
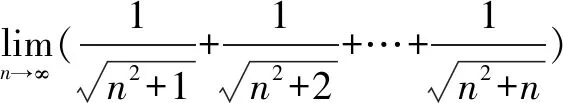
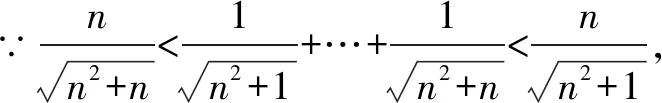
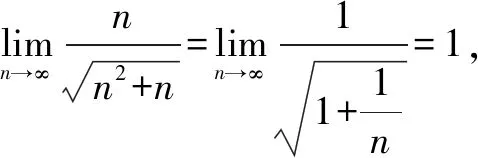
说明：此方法的关键是找出前后两个函数，且这两个函数的极限相同.

5.利用重要极限

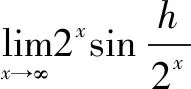
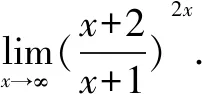
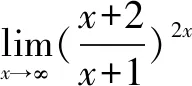
说明在求极限过程中，要对函数进行适当变形，使其变成重要极限的形式，再用重要极限求解.

6.洛必达法则

定理设(1)当x→a时，函数f(x)及F(x)都趋于零;

(2)在点a的某邻域内(点a可以除外)f′(x),F′(x)都存在且F′(x)≠0

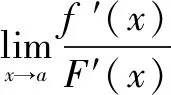
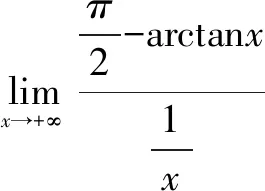
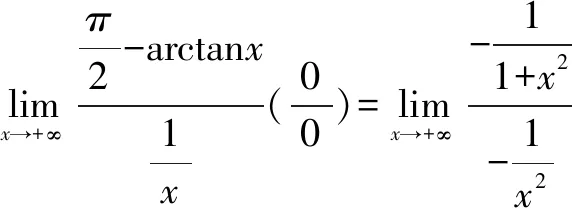
说明(1)把定理中的x→a换成x→∞，把(2)换成当|x|>N时，f(x),F(x)都可导且F′(x)≠0，结论仍然成立.

(2)洛必达法则是求未定式的一种有效方法，但最好能与其他求极限的方法结合使用.例如要求的极限函数是幂指函数的形式u(x)v(x)(u(x)>0,u(x)≠1时，通常先把函数转化成指数函数u(x)v(x)=elnu(x)v(x)=ev(x)lnu(x)，再求极限.

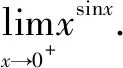
解这是未定式00,设y=xsinx，取对数得lny=sinxlnx，又

因为y=elny，

而limy=limelny=elimlny(x→0+)，故

(3)本节定理给出的是求未定式的一种方法· 当定理条件满足时'所求的极限当然存在(或为∞)'但定理条件不满足时'所求极限却不一定不存在.

二、结论

函数极限的求法是多样的，除了本文的这几种方法，还有其他的求解方法，因此在解题过程中要根据函数本身的特点来选择合适的方法，以简便计算.