高压电源应用中LCC谐振变换器的研究综述
汪邦照,刘艳丽,汪方斌,王 磊
(1.合肥华耀电子工业有限公司,安徽 合肥 230031;2.安徽建筑大学 机械与电气工程学院,安徽 合肥 230601)
0 引 言
目前,国内采用的大功率高压电源基本工作于电流断续模式,电力电子变换器处于软开关工作状态,开关损耗大大降低。但另一方面,工作于电流连续模式下的高压电源能大幅度提高谐振变换器的输出电流从而提高输出功率[1]。Alstom公司的科技人员在文献[2]中也介绍了大功率高压电源的电流连续工作模式,并提出了一种减少开关损耗的最优化算法。可见,高压电源的电流断续和电流连续工作模式各有其优点,鉴于处于电流断续工作模式下的高压电源已有很丰富的开发经验,因此本文仅对电流连续工作模式下高压电源的分析方法、优化算法和控制方法展开讨论。
大功率和中高压电源的谐振信号变换器多为三相LCC串并联方式结构(如图1所示),三相LCC串并联结构谐振变换器同时兼顾了串联和三相并联谐振变换器的优点,具有效率高、特别是其功率密度高能将其体积做到很小[3-5]。文章介绍了可用于这种拓扑结构的谐振电路的几种分析和设计方法,这些方法都能建立LCC串并联谐振电路的数学模型,然后,基于数学模型可以用仿真手段分析电路的性能,从而指导电路设计,可在后期的实验环节节省大量人力和财力。
并且研究发现,LCC串并联谐振电路是强非线性系统,电路中大部分参数是相互关联的,针对不同的电路特性对元件的选择有一定的限制,这些因数导致了这种拓扑结构的电路分析和设计过程十分繁琐。为了根据电路的设计要求找出一个最优的设计方案,本文提出了一种基于Pareto的多目标遗传算法SPEA2,相对于传统的优化算法,遗传算法SPEA2在谐振电路性能优化应用中有明显的优势。
最后,文章还特别提到了一种适用于谐振控制电路的一种最优轨迹驱动控制设计方法,该控制方法在系统信号响应时间、稳定性、短路时的承受能力均有很好的控制能力。
图1所示Lr为包含了变压器的漏感串联谐振电感,Cr为串联谐振电容,Cp为包含折算后的分布电容的并联谐振电容。
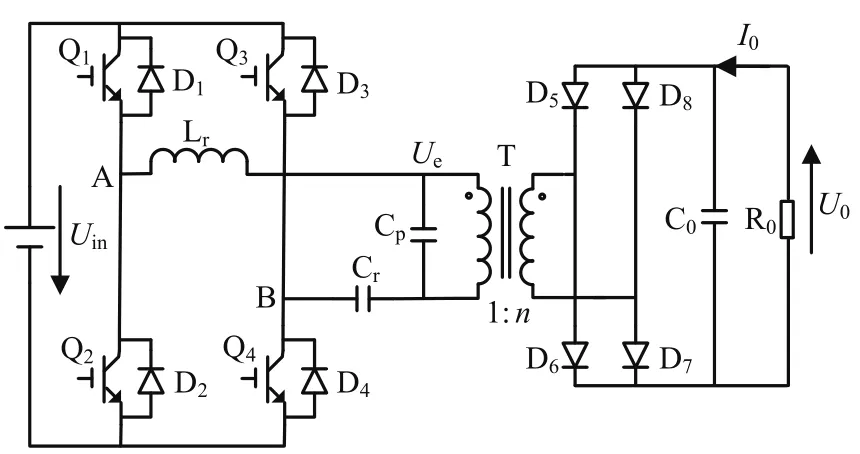
图1 高频直流电源谐振电路拓扑
1 LCC谐振变换器的分析方法
1.1 时域分析法
LCC谐振电路常见的6种谐振状态如图2所示。根据这6种谐振状态,用欧姆定律即可求出每个时段内谐振电流和电容电压为状态变量的时域方程。

图2 LCC谐振电路的6种谐振状态
时域分析方法的优点:精确度最高。缺点:数学模型很复杂,而且通过时域数学模型分析电路稳态性能比较困难。
1.2 状态平面分析法
状态平面分析法由Oruganti R.和 Lee FC.于1988年提出,它是建立在时域数学模型基础上描述谐振电路规范化状态变量变化轨迹的一种分析方法[6]。简单点说,就是通过这种方法,可以把时域数学方程中状态变量的变化轨迹用图形描述出来。
如图3所示以电容电压和谐振电流为状态变量,建立了状态图,即LCC谐振电路的稳态轨迹。图2中的每个谐振时段对应于图3中的一个圆弧,例如:图2(a)时段对应U′CN(i′CN)坐标轴AB段圆弧;(b)时段对应UCN(iCN)坐标轴CD段圆弧;(c)时段对应于UCN(iCN)坐标轴DE段圆弧。另外,图2(d)、(e)、(f)时段与圆的下半周对应。
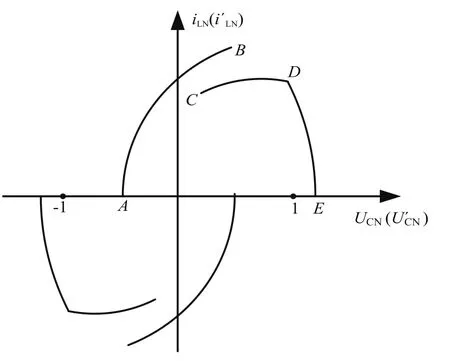
图3 LCC谐振电路的稳态轨迹
状态平面分析法优点:把原来的时域模型中状态变量的变化轨迹图形化了,比较直观,而且精确度和时域模型一样高。缺点:建模过程很复杂,电路稳态性能通过此方法仍较难分析。
1.3 基波分析法
基波分析法是一种广泛应用于谐振电路的近似分析方法。分析过程是:取电流基波分量和高频变压器一次侧交流电压,得到谐振变换器的等效电路(采用正弦稳态分析方法),如图4所示为其等效电路。然后在等效电路基础上推导数学模型,最后根据推导的数学模型确定一种符合系统设计需要的最佳交流电路参数。
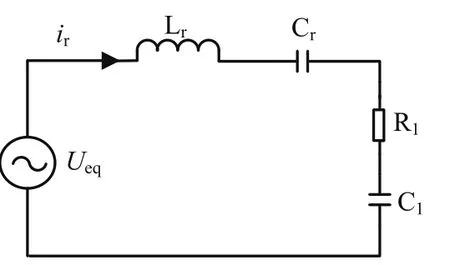
图4 LCC谐振电路的等效电路
图4中,R1和C1分别为原电路变压器侧等效电阻和电容。
基波分析法的优点:容易建模,通过此分析方法可以分析电路稳态性能,并用于指导电路设计。此法缺点:很难分析电路暂态过程,且分析精确度不高。
1.4 动态相量分析法
1991年SANDERS SR等人提出动态相量法[7],目前,国内外许多技术专家已在实际应用进行了研究,如:电力系统和电力电子电路[8-11],并证明了这种动态相量法具有数学仿真快和精度高等诸多优点。
动态相量法的基本建模原理如下文所述。
对于时域中波形是连续并且变化快速的信号x(τ),波形可以通过傅里叶级数描述为

式中,ωs=2π/T0;时间间隔τ∈(t-T0,t];〈x〉K为第K阶“动态相量”,它是时间的函数。
第K阶动态相量的微分特性可描述为

基于以上动态相量的基本理论,即可成功建立3种数学模型:基于动态相量LCC谐振电路的大信号模型、基于动态相量LCC谐振电路的稳态模型和基于动态相量LCC谐振电路的小信号模型。其中,大信号模型可用来分析系统的暂态过程;稳态模型可用来分析稳态时系统的电路特性;在频域内分析系统动态响应可以用基于动态相量LCC谐振电路的小信号模型进行分析。
(1)大信号模型的仿真结果
用Matlab 对LCC谐振电路大信号模型进行仿真。电路仿真时的条件描述如下:电路仿真时的算法采用ode23,仿真时的步长参数为1 μs,电路仿真参数为:Uin=100 V;R0=30 Ω;Lr=100 μH;Cp=Cr=1 μF;C0=47μF。
算例:如图5所示,在3 ms时刻,开关频率fx由25 kHz跃变到20 kHz时,谐振电流和输出电压仿真曲线如图5所示。可见在开关频率发生跃变时,动态相量曲线很好地包络了时域仿真曲线。
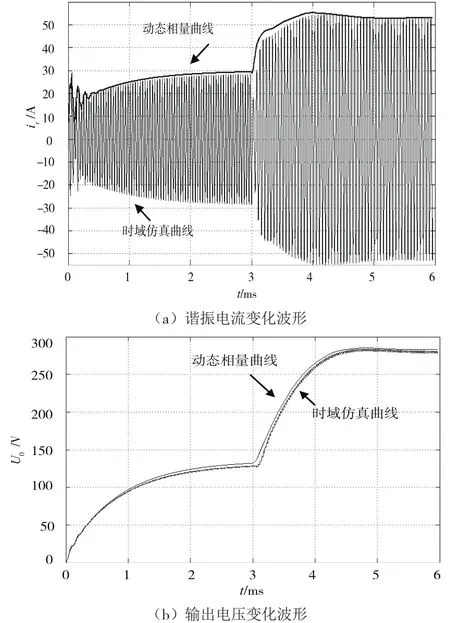
图5 开关频率跃变时的动态相量模型与时域模型波形比较
(2)稳态模型仿真曲线
按照稳态模型可求得电压/电流传输比表达式:
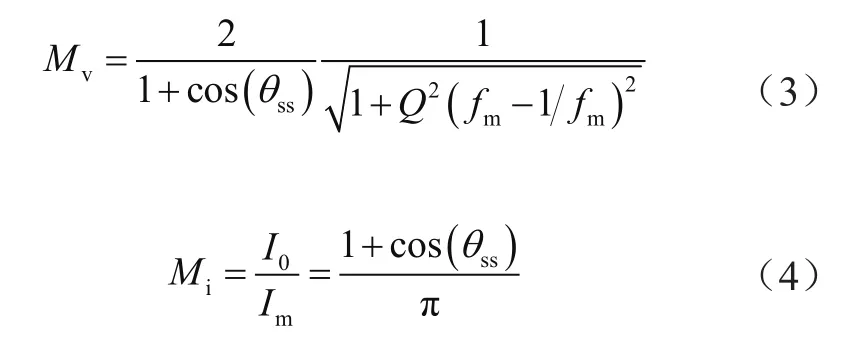
式中,Q为电路品质因数;θss为Cp充电时段对应的角度;Im为谐振电流幅值;fm为开关频率与谐振频率比值。
根据式(3),通过计算机进行仿真后即可得到在品质因数为1和品质因数5时的电压传输比关系曲线。每组曲线里又有不同θss,如图6所示。
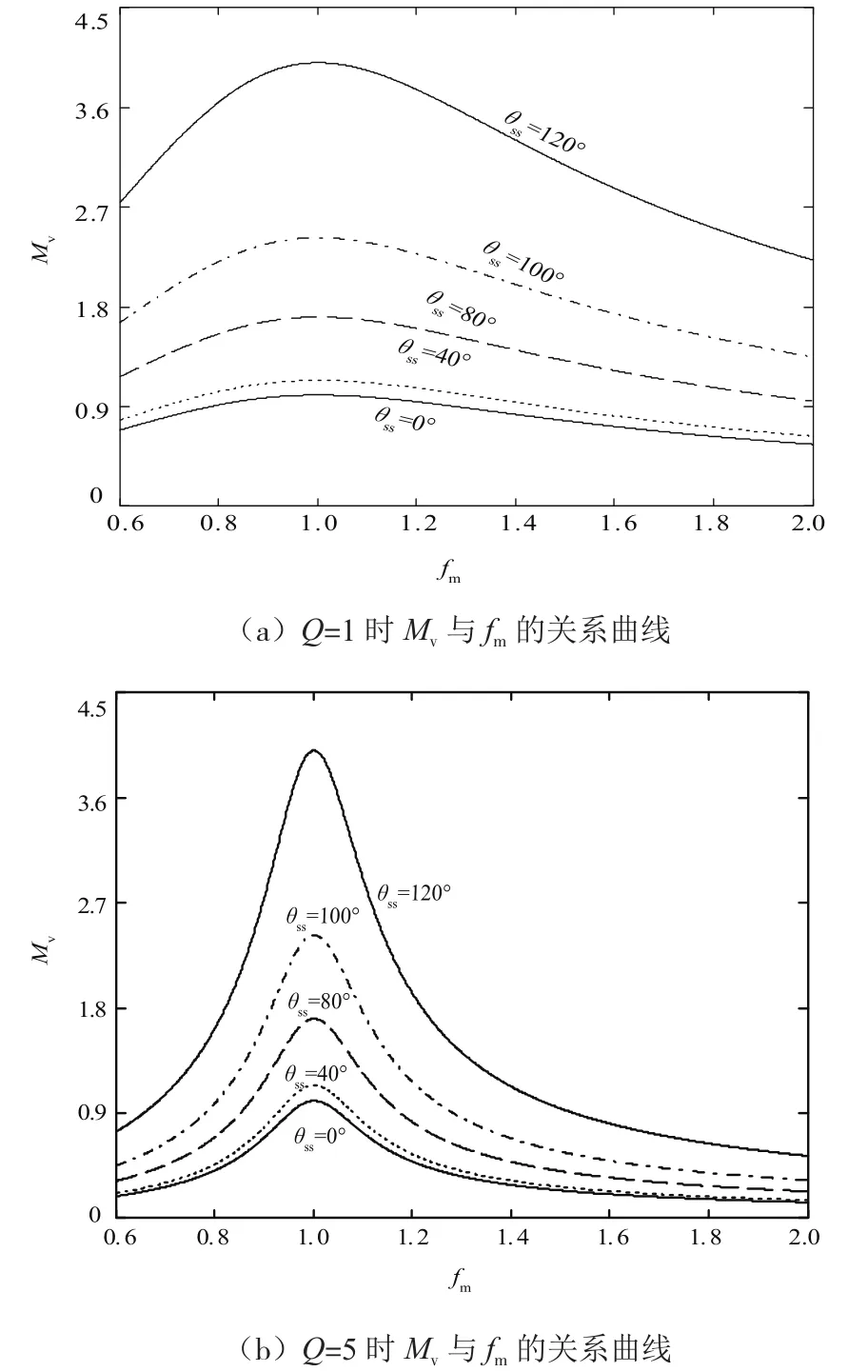
图6 品质因数不同时电压传输比的关系曲线
根据式(4),电流传输比关系曲线如图7所示。

图7 电流传输比的关系曲线
动态相量法优点:(1)建模容易;(2)仿真精确度介于时域分析法和基波分析法之间,但仿真速度比时域模型快得多(大约20多倍);(3)基于动态相量法建立的大信号模型可用于分析电路的暂态过程,而稳态模型可用于分析电路性能并指导电路设计;(4)动态相量法对LCC谐振电路的建模为其小信号分析打下了基础,进而全面了解系统的动态响应特性;(5)在仿真环节就已经掌握了电路的暂态和稳态性能,为电路的设计参数的选择服务。
缺点:随着谐波次数的增加,谐振电路分析的精确度也增高,但是数学模型的建立过程也越来越复杂。
2 LCC谐振变换器的多目标优化算法
2.1 基于PARETO的多目标遗传算法
1985年第一个多目标演化遗传算法首次出现,该算法是基于向量评估的遗传算法(Vector Evaluated Genetic Algorithm,VEGA)。后来许多学者在多目标优化研究领域探索的同时提出了多种解决方法。例如,比较常用的基于Pareto遗传算法[12-14]有:仿Pareto遗传算法(Niched Pareto Genetic Algorithm,NPGA)和增强Pareto进化算法(Strength Pareto Evolutionary Algorithm,SPEA)。多目标优化遗传算法很适合LCC谐振电路的设计。它的主要特点是只需要提供目标函数的信息,就可找到最优解(对搜索空间不连续不可微分的也适用),因此选择遗传算法作为LCC谐振电路的多目标优化方法是合适的。
多目标优化问题的数学描述如下:

式中,X为决策变量空间;x为带有n个决策变量的向量;Y为目标函数空间;y为带有n个目标函数的向量;e(x)为m个约束函数。
多目标优化的主要问题是:多个目标之间相互约束,对其中一个目标优化就会损害另一个目标的利益,因此很难客观地来评价多参数目标解的优劣。
如图8所示为SPEA2算法流程图。图中,T为遗传算法中最大的进化次数。
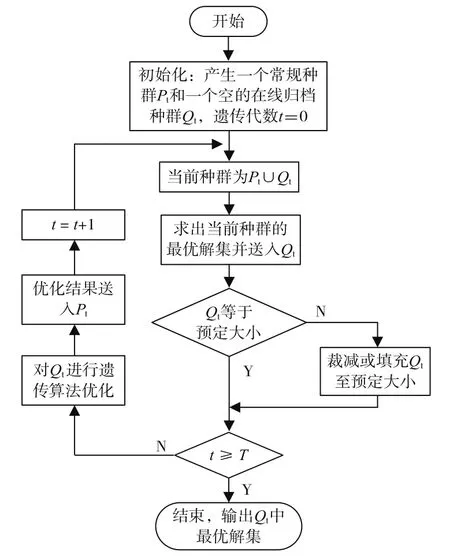
图8 遗传算法SPEA2流程
2.2 算法验证
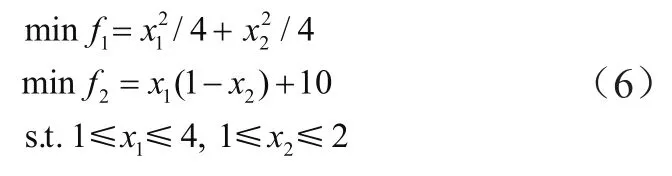
式(6)为SPAE2算法验证算例。
基于SPAE2算法获得的Pareto前沿如图9所示。本算法采用Matlab仿真,源程序代码中初始种群个体数目为50,最大遗传代数为100。可以看出,采用此算法能获得大量均匀的Pareto最优解集。

图9 遗传算法SPEA2获得的Pareto前沿
2.3 在LCC谐振电路设计中用多目标优化算法的原因分析
国外已有在LCC谐振电路中设计中用优化算法的先例,如Alstom公司的技术人员在大功率高压电源的电路参数设计中为减少开关损耗而用到了遗传优化算法。但值得指出的是,他们用的仅仅是单目标优化算法,而本文提到的多目标优化算法能以多个优化对象为目标进行优化。
多目标优化算法用于LCC谐振电路优化设计的优点:(1)为了达到设计目的,以其设计目标为优化对象进行仿真计算后立即可得到一组供技术人员参考的电路参数;(2)在实验环节可以节省大量的人力和财力投入。
3 LCC谐振变换器的最优轨迹控制
最优轨迹控制法由Oruganti R.和 Lee F.C.于1985年提出[15,16]。他们在文献[16]中对比串联谐振电路的变频控制、电容电压控制、二极管导通角控制和最优轨迹控制。从系统响应时间、稳定性、短路承受能力等方面对这4种控制方法进行比较,最后得出最优轨迹控制在这些方面均处于优势的结论。但值得指出的是,虽然最优轨迹控制有很多优点,但它在应用上实现比较困难。
就大功率高压电源应用场合的特殊性来看,对高压电源的要求是抗短路能力强,且在火花发生以后为了快速恢复电场能量还要求系统响应时间短。由此可见,最优轨迹控制将来不失为大功率高压电源谐振变换器控制方法的一种最好选择。
简单地说,最优控制法则就是制定控制命令,这个控制命令主要任务由DSP进行最优开关时间的计算,即计算出什么时候开关管导通或最佳关断时刻。此控制方法是以谐振电路电感电流和电容电压为状态变量,从而建立状态图,在状态平面法建模的基础上实施。期望在最短的时间内实现两个不同稳态轨线的转换,即达到它们期望的稳态轨迹并保证良好的动态性能,从而减少暂态振荡。其控制框图如图10所示。

图10 最优轨迹控制框图
4 结 论
文章介绍了电流连续模式下LCC谐振变换器的几种分析方法,提到了可用于这种强非线性电路拓扑结构的一种多目标优化算法,最后介绍了一种最优轨迹控制方法。这些分析方法、优化算法和控制方法已有一些专家和研究人员展开了研究,其研究目的在于改善LCC谐振电路的系统性能,指导电路设计和调试,以达到预期的设计和控制目标。文中LCC谐振电路的分析方法、控制方法和多目标优化算法对于推进我国大功率高压高频电源应用领域的研究和实践有一定的参考价值。

