光纤光栅土压力盒设计

邢心魁，宁博宏，林揽日，丁家玮

(1.桂林理工大学土建学院，广西桂林 541004；2.广西有色金属隐伏矿床勘察及材料开发协同创新中心，广西桂林 541004；3.广西岩土力学与工程重点实验室，广西桂林 541001)

0 引言

在岩土工程领域，由于土压力测量(如荷载大小，分布情况等)的需求，使得许多学者开始根据不同需求研发新型土压力传感器，其中常用的传感器以膜片作为弹性敏感元件，根据膜片的变形转换成其他可测物理量，以此得到外界土压力情况。如刘开源[1]等研究的FSR (force sensel resistance)是一种压阻式柔性传感器，将含有导电物质的高分子材料夹在两层聚合物膜片中间，当膜片受法向作用时，高分子材料的变形使膜片中间产生导电通道而降低FSR电阻，通过电阻-电压的关系测量土压力值；廖波[2]等设计了单、双层两种结构的薄膜压阻式传感器，通过对比研究发现双层结构的压阻特性更好，灵敏度更高，增大压力后电阻减小更明显。徐光明[3]等研究了一种电阻应变式微型传感器，将膜片的变形转变成应变计电阻信号的变化，其较好的兼顾传感器性能品质指标与柔度因数(与传感器膜片直径，厚度，刚度及土体刚度有关的设计参数)之间的关系。许高斌[4]等设计了一种用于复杂环境下的谐振式压力传感器，通过硅岛将传感器膜片受垂直压力时的变形转化成谐振器沿膜片径向的侧向振动，以此根据测量的振动频率与应力关系曲线得到土压力值，改进了这类传感器常出现的精度受谐振质量影响而降低，敏感结构部分受温度影响较大，存在不稳定激励与检测等问题[5-7]。

以上阐述的传感器也可根据将膜片变形转换成的物理量特性统称为电磁类传感器(振弦式，电阻应变片式，压阻式，电容式，压电式等)，虽然有各自不同的优势，但是在室外大型工程里，也存在着耐久性和稳定性不足，抗电磁干扰能力差，测量信号远距离传输困难等缺点[8]。针对这些问题，国内外学者正积极研发一种新型无源传感技术—光纤型传感器，近年来由于其适用于地质环境复杂，施工条件恶劣的场所，同时耐腐蚀，灵敏度高，尺寸小，不受电磁干扰，可串联等优势，被广泛应用于实际工程中。目前在工程中采用的光纤光栅土压力盒通常是用胶粘剂加封装材料将光纤光栅直接粘在受压膜片上，当外界的温度，压力，振动等作用，引起受压膜片产生变形时，粘贴在膜片上的光纤光栅的周期Λ及其有效折射率neff会相应发生变化，最终使光纤光栅反射光的波长λB产生一定的漂移量，如式(1)[9]。由此我们可以根据反射光波长的变化来感知外界被测物理量的变化情况。

λB=2neffΛ

(1)

本文以土压力盒所受的均布荷载作为被测物理量，由光纤光栅土压力盒测量原理可知，受压膜片的变形，是联系均布荷载和光纤光栅波长变化的中间量(式(2)[10])。

ΔλB/λB=(1-Pe)ε

(2)

式中：Pe为玻璃光纤有效弹光系数，典型的二氧化硅光纤取0.22；ΔλB为波长差，nm；ε为光纤光栅应变，这里假定在理想情况下光纤光栅轴向拉伸量与土压力盒受压膜片弯曲时的径向应变量一致。

膜片的参数，决定土压力盒的灵敏度和量程，决定压力盒的工作特性。因此要得出荷载和光纤光栅波长之间的关系，首先要研究荷载与受压膜片变形之间的关系。本文通过弹性力学知识，利用均布荷载与受压膜片挠度关系的力学模型，推导出受压膜片径向应变与荷载之间关系式，并与ANSYS有限元分析结果进行对比，选取合理的受压膜片，进而设计出光纤光栅土压力盒结构模型。

1 土压力盒受压膜片荷载与变形特性的理论分析

1.1 受压膜片的挠度计算

光纤光栅土压力盒作为新型测量传感器，因其简便的操作常被用于测量岩土体内的应力，这时土压力盒的受压膜片将受到均布荷载的作用。将受压膜片近似为一个等厚度的圆形薄板，具有结构对称和荷载径向对称的特点，图(1)、图(2)为土压力盒力学模型。利用弹性力学的知识建立在极坐标下薄板弯曲的基本微分方程，如式(3)[11-13]所示。

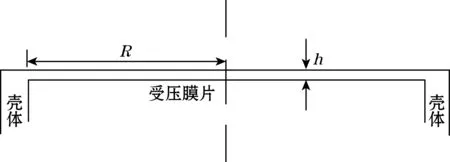
图1 土压力盒局部图

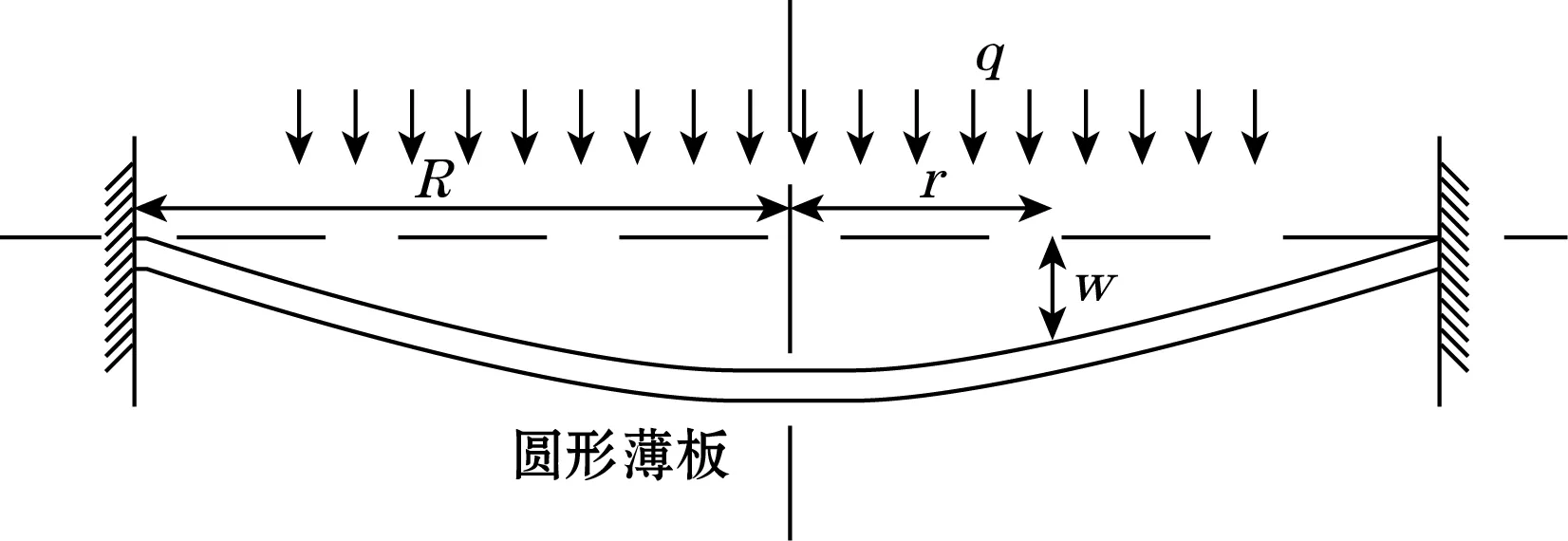
图2 受压膜片近似图

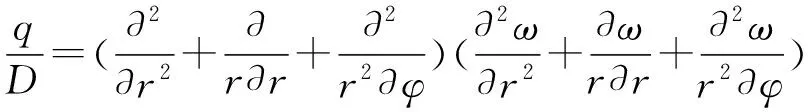
(3)

式中：q为板面所受的均布荷载，MPa；D为膜片抗弯刚度，D=Eh3/(12-12μ2)(其中μ为泊松系数；E为弹性模量，GPa;h为受压膜片厚度，mm)；r为以圆心为中心的半径，mm；φ为极坐标中的角度，(°)；ω为半径在r处的挠度，mm。

目前已有大量文献[14-15]，求解过此方程，最终可得到弯曲薄板的挠度为

(4)

式中R为受压膜片半径，mm。

1.2 受压膜片的径向应变

根据圆形薄板的结构与荷载的对称性，取距圆心r处的圆周，圆周上各点弯曲情况一致，因此圆周上的受力情况可以比拟为矩形截面板的受弯状态。当研究整个圆形薄板周边的受力状态时(即r=R)，图3中的圆形薄板可近似成矩形截面板，如图4所示。

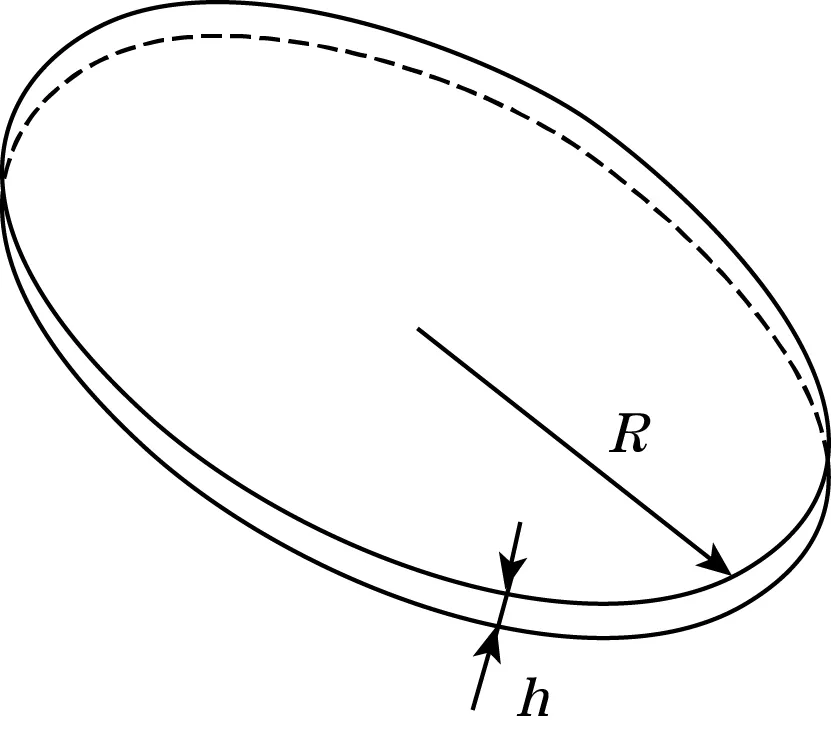
图3 圆形薄板

图4 矩形薄板

薄板在受弯情况下，应力与弯矩的关系为

σ=My/I

(5)

式中：σ为正应力；M为弯矩；I为惯性矩，I=πRh3/6；y为所求正应力处的点到中性轴的垂直距离(对薄板表面，y=h/2)。

再通过挠曲线近似微分方程为

(6)

将式(4)、式(6)代入式(5)，最后整理得到圆形薄板径向应变为

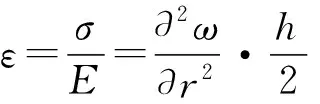
(7)

2 有限元分析及验算

使用有限元软件ANSYS进行分析，采用4节点的shell181单元，此单元适用于具有一定厚度的壳体结构；膜片材质使用合金钢，其弹性模量E=199 GPa，泊松比μ=0.3；取受压膜片半径R=65 mm，厚度h=1.1 mm(下文会介绍膜片半径和厚度的取值原则)；单元划分如图5所示。

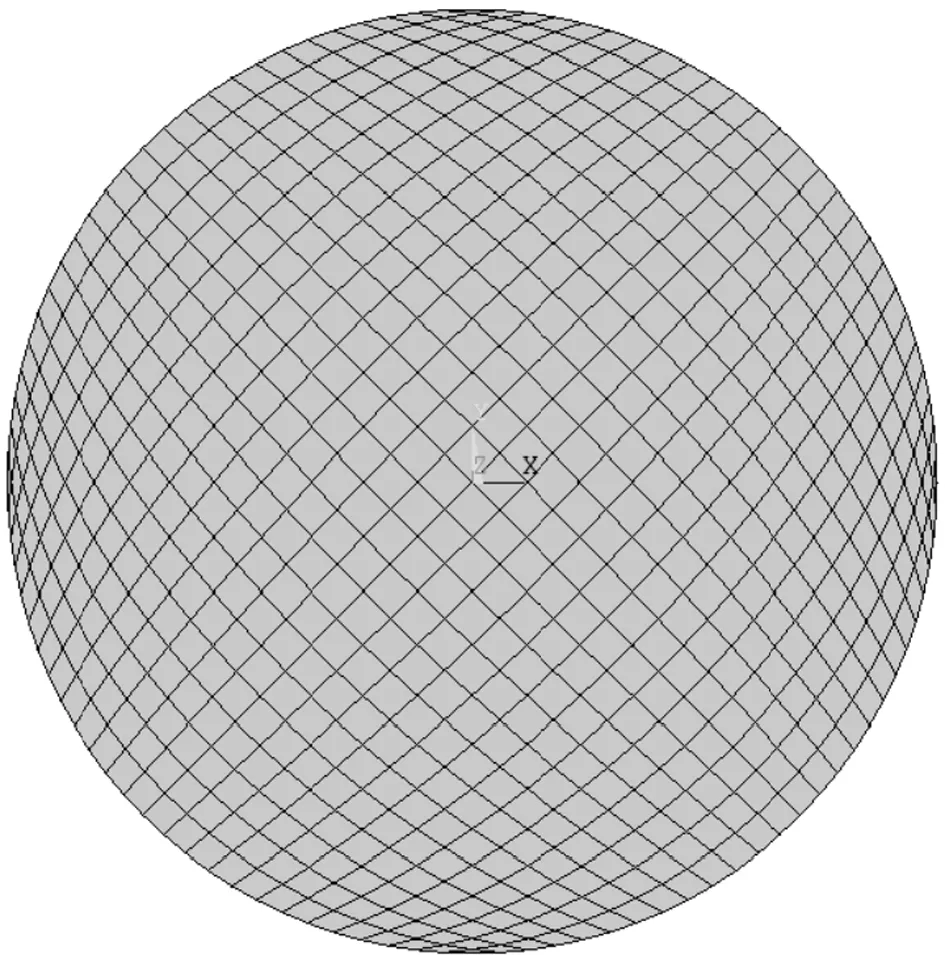
图5 有限元网格划分

边界采用周边固支的方式，均布荷载垂直施加在板面上。计算所得板面径向应变云图见图6，应变在中点处为正值最大，往边缘移动正值减小，达到零值后变为负值，并在边界处达到绝对值最大。

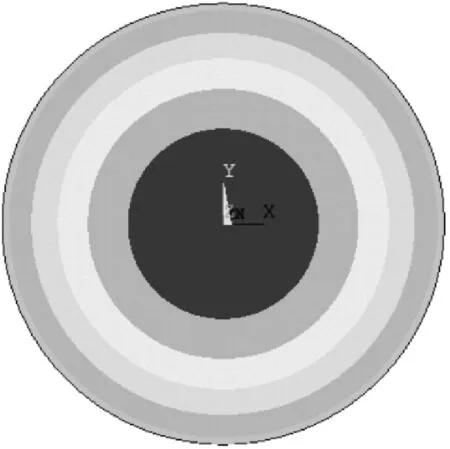
图6 应变云图

为了对比两种方法的一致性，将板面中心处在不同荷载下有限元分析和式(7)计算结果对比，如表1所示。

表1 有限元计算与理论计算的应变值对比

由表1结果可见，两者数值差距极小。同时本文还对不同半径与厚度的受压膜片进行了系列计算，两种方法所得误差均在1%以内。因此在后续计算中可直接使用式(7)进行运算。

3 光纤光栅土压盒受压膜片的设计计算

为了使设计的光纤光栅土压力盒在设定的量程内，安全且具有较高的灵敏度。需要同时考虑受压膜片和光纤光栅两者材料的屈服极限，以此确定能满足极限条件的受压膜片尺寸。

3.1 受压膜片的极限荷载

在膜片受力发生变形时，当应力超过弹性极限时将会发生塑性变形，应变无法完全恢复，土压力盒失效。由于大多合金钢没有明显的屈服点，规定以残余变形的应力值作为其屈服极限[16]，本文采用σ0.2=900 MPa的合金钢。

乐孜纯[17]对膜片的极限荷载进行了计算分析，他认为屈服应力数据点接近米塞斯(Mises)屈服条件，通过查阅文献[18]得到周边固定等厚度圆形薄板的无量纲化极限荷载为

(8)

式中：Pb为集中力或均布荷载的合力，Pb=πqR2；Mb为板横截面上单位宽度作用的弹性极限弯矩，Mb=σ0.2h2/6。

经整理得q=1 875h2/R2，因此，只要规定了最大量程qmax以及半径R，由式(9)求解出为了使受压膜片正常使用所需要的厚度h。

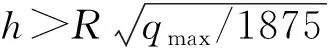
(9)

3.2 光纤光栅的长期允许应变

由于光纤光栅是跟随受压膜片发生变形的，因此应使受压膜片在受到最大量程的面应力时，所产生的最大应变值小于光纤光栅长期允许应变，才能保证光纤光栅正常作用。目前市面上裸光纤光栅的极限应变大约在3 000～5 000 με[19-20]，本文采用应变量程在3 000 με左右的光纤光栅。

式(7)在受压膜片原点处(即r=0)应变值最大，这时最大应变为εmax=3qR2(1-μ2)/(8Eh2)，将最大量程以及半径代入式(7)，便能求解出满足量程的受压膜片厚度所需满足的条件，式(10)。

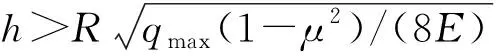
(10)

最后，在设计受压膜片尺寸时，其厚度h必须同时满足式(9)、式(10)，则能保证施加的面应力在达到最大量程后，受压膜片不会产生塑性变形。

3.3 受压膜片的尺寸设计与分析

3.3.1 膜片尺寸的确定

根据上文所推导的公式，可以确定受压膜片的尺寸，过程按流程图7进行计算。由于在制作受压膜片时还应该考虑到加工工艺水平，因此膜片厚度的数值不能过小。

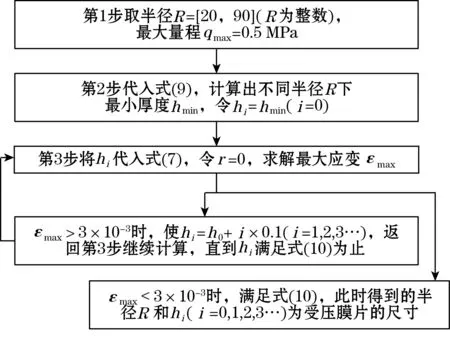
图7 受压膜片尺寸计算流程图

从传感器的灵敏度考虑，内部应变最大值越大越好，因为在相同荷载作用下得到的变形越大，传感器越灵敏。从上述过程计算得到的尺寸中，选择变形较大的膜片尺寸，如表2所示。

表2 不同尺寸的受压膜片

3.3.2 膜片尺寸的分析

对于光纤光栅土压力盒而言，传感光栅的长度影响测量点的精度，长度越小，测量点越精确，但是其反射率也会越低，带宽越宽，以至于很难达到相应的要求。因此综合考虑，在大多数应用中，普通传感光栅的物理长度推荐为10 mm[21]。将光栅中心粘贴在受压膜片原点处，这时沿某一直径距膜片原点5 mm的范围内是粘贴光栅区段。

将表2的8组尺寸代入式(7)中，施加0.5 MPa均布荷载，计算每组尺寸在半径为0、1、2、3、4、5 mm点处的应变值，最终通过折线图8可以看出，膜片尺寸越大，粘贴光栅区段变形越平缓(其他均布荷载值下有相同规律)。

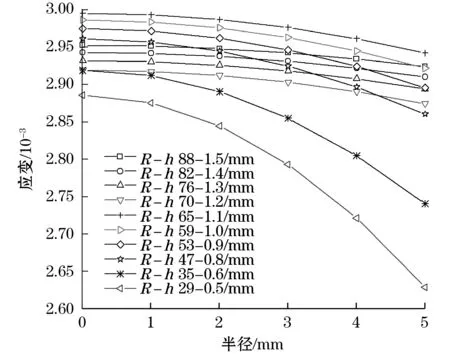
图8 每组尺寸在0.5 MPa均布荷载作用下的应变值

由于式(1)是对光纤光栅在轴向拉压的情况下建立的，因此光栅在均匀轴向应变下，其反射光波长漂移量才与外界应变成良好的线性关系。但对土压力盒受压膜片是弯曲变形，会使光栅产生非均匀应变，使得理论计算与实际测量结果有一定出入，为了减小这一原因产生的影响，尽量在选取膜片尺寸时，选择膜片粘贴光栅区段变形相对均匀的尺寸。现进一步分析各尺寸膜片在粘贴光栅区段的最大应变差值比(即r=0处与r=5处的应变差值比)，所得结果如表3所示。

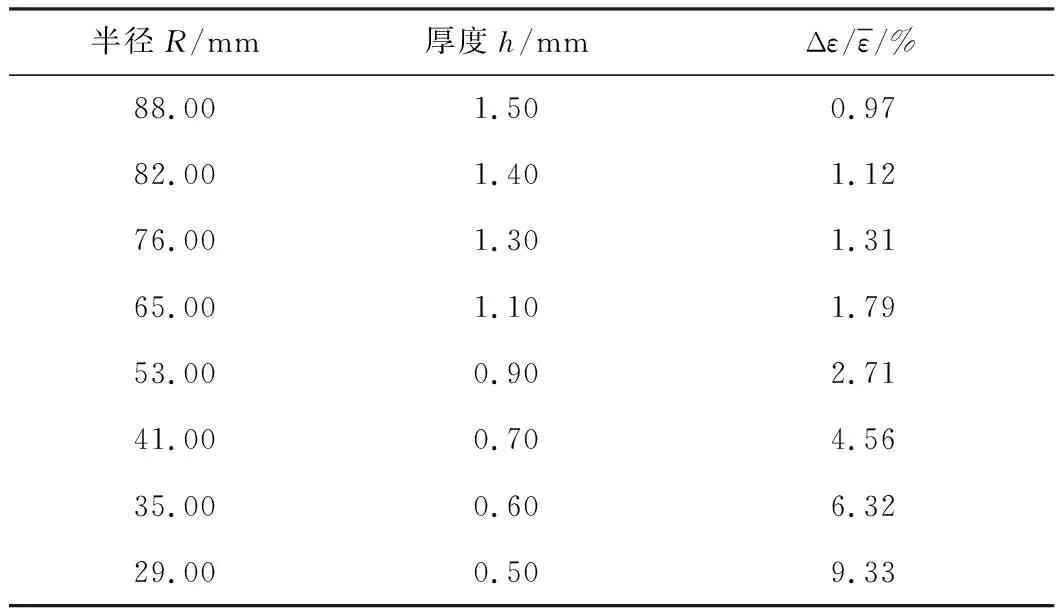
表3 不同尺寸膜片的最大应变差值比

由表3可见，宜选取最大应变差值比在5%以内的膜片尺寸，即半径-厚度为35-0.6和29-0.5的两组尺寸由于膜片不均匀弯曲引起光栅不均匀应变而导致实际测量有较大误差不宜选用。

4 土压力盒整体结构设计

在设计土压力盒整体结构时，应考虑土压力盒对土体的干扰程度，主要体现在以下相容性上[22]：强度相容，即土压力盒不能或尽可能小的影响到被测介质的强度；界面相容，土压力盒与被测介质相接触部分的材质要相容；尺寸相容，则是在选取土压力盒尺寸时不宜过大，以保证能与被测介质变形相匹配；场分布相容，土压力盒的埋入不能影响被测介质原应变、温度场等的分布。

图9是土压力盒的整体结构。在设计时，土压力盒除了要考虑自身对土体的影响外，还需要考虑其自身在实际测量时会受到外界因素的影响。如土压力盒整体的厚度(H)与直径(2Rout)比越小，所测得的应力与该点扰动时的真正应力越相近，建议比值在0.1到0.2之间[23]。

图9 土压力盒结构图

由于采用的光纤光栅材料和加工工艺的差异，土压力盒最终应变灵敏度和量程需要标定后才能实际应用。而在进行砂标时，应对土压力盒先行加卸荷载几次，再正式进行标定，以消除非弹性变形。

5 结束语

(1)目前对光纤光栅土压力盒的变形研究，大多是在压力与膜片的挠度关系上，本文在现有等厚度薄板挠度模型的基础上，研究了膜片的径向应变分布规律并推导出径向应变公式，与光纤光栅工作机理直接对应，通过与有限元分析结果对比，证明采用理论公式计算受压膜片的应变是可行的；

(2)光纤光栅土压力盒设计需要综合考虑多种因素，包括材料强度、量程、精度、加工和封装工艺以及测试对象的要求等，本文重点以压力盒与光纤光栅两种材料强度及量程作为约束条件对膜片尺寸进行了确定，最终在不同约束条件下发现单一考虑某种材料强度，难以保证压力盒正常工作；

(3)在光纤传感器原理的基础上，考虑受压膜片为非均匀应变，因此本文通过分析不同尺寸的受压膜片，研究出在同时满足相关条件下受压膜片尺寸越大，粘贴光栅的中心区段变形越平滑，其变形越均匀，测试效果越好，反之受压膜片尺寸越小，膜片的非均匀应变越影响实际测量，其中本文设计的膜片半径在40 mm以下的压力盒其黏贴光栅中心区段的最大应变比大于5%，不宜选用。但最终尺寸的选择还需要结合实际工程的需要，综合考虑。

本文研究内容是在单一作用力下进行分析设计的。实际应用中，温度，振动等其他因素对光纤光栅土压力盒测试都有一定的影响，因此在复杂条件下，光纤光栅土压力盒设计还有待进一步研究。