高温薄膜快响应传感器的设计及其仿真优化

于广滨，于明新，戴 冰，陈 杰，张洪泉

(1.哈尔滨理工大学机械动力工程学院，黑龙江哈尔滨 150080；2.哈尔滨学院工学院，黑龙江哈尔滨 150080；3.黑龙江大学电子工程学院，黑龙江哈尔滨 150080)

0 引言

随着科学技术的不断进步，温度传感器的发展趋向于高温、快速响应方面，尤其是测量瞬态温度的薄膜传感器具有重要实际应用价值[1-2]，薄膜温度传感器体积小，响应快，精度高，稳定性好的特点，能够满足对温度测试的小型化、集成化、多功能化、智能化的发展需求,在MEMS、集成电路、微纳器件等领域具有广阔的应用前景[3-6]。

Y. C. Zhang等[7]研究了关于薄膜热电偶传感器的工作原理，优缺点和制造技术，并针对校准问题提出了解决方案；赵源深[8]等综述了薄膜热电偶的发展，具体介绍了薄膜临界厚度的确定、制备工艺等关键技术,并对其未来发展做出了展望；2011年，黄春峰等[9]成功制备了一种独立传感单元可贴敷在发动机壁面进行温度测试的微型薄膜热电偶，在许多工程中获得实际应用；K. G. Kreider等[10]研制出了BS-1和BS-2型薄膜热电偶，用于测定柴油机气缸盖的瞬变温度，邓进军等[11]设计了一种50～400 ℃范围内精度高，引线方便的薄膜瞬态温度传感器。

传统的薄膜传感器由于其结构较小，导致在实际工程应用中很难长期使用，国内外的学者们通常采用的方法是将薄膜传感器进行封装处理，进而减小工作环境对传感器测温的影响，在进行封装过程中多采用经验估计的方法，但忽略了传感器的结构特征，流场分布特征等影响因子，因此难以得出精确的数值结果。

针对上述方法的不足，本文采用流热耦合多物理场仿真分析的方法对高温薄膜传感器进行流体热力学仿真分析，量化流场分布和传感器的结构对传感器测温产生的影响，推导出传感器结构与响应时间和测量误差之间的数学模型，并使用粒子群算法拟合仿真结果，获得计算方程用以求解最佳传感器结构尺寸。

1 高温薄膜快响应传感器的工作原理及结构设计

1.1 薄膜热电偶的工作原理

薄膜热电偶测试的基本原理与体热电偶相似，均为赛贝克效应，该效应的表述为：由一对热电性质不同的材料A、B搭接成的闭合回路，当2个连接处的温度不同时(温度较低的连接处被称为冷端，温度较高的连接处被称为热端)，闭合回路中会产生温差电动势(即热电势)EAB，热电势的表达公式为

(1)

式中：SAB(T)为热电偶温度T时的赛贝克系数；T0为热电偶冷端连接处的温度；T1为热电偶热端连接处的温度；eAB(T0)为温度为T0的连接处的热电势；eAB(T1)为温度为T1的连接处的热电势。

热电偶的赛贝克系数SAB(T)数值的大小和符号，取决于组成热电偶的2个导体的绝对赛贝克系数之差，则式(1)可改写为

(2)

式中：SAB(T0)为温度T0时的绝对赛贝克系数；SAB(T1)为导温度T1时的绝对赛贝克系数。

测量较高的热电偶的冷端通常为参考端，当参考端的温度恒定时，即温度T0恒定时,SAB(T0)为常数，则热电势EAB值的大小仅与热端的温度T1有关，式(2)可改写为

EAB=SAB(T1)-SAB(T0)=SAB(T1)-c

(3)

1.2 高温薄膜快响应传感器的设计

本文提出了一种单片集成高温薄膜快响应传感器，采用铂铑10 -铂薄膜热电偶冗余设计方法，在Al2O3陶瓷基板正反两侧设计两组电极实现冗余设计，Al2O3陶瓷基板厚度为0.15 mm，电极宽度为0.1 mm，厚度为0.05 mm，从而达到测温结构的小型化。

为实现热电偶的快响应，利用三角形结构设计，热偶感温点设置在三角形顶角处，这样可以达到感温点的热容量小，也就是感温点的物理体积小的特点，满足传感器的快响应技术要求。同时，热电偶三角形结构设计，可最大限度具有抗环境振动和热气流冲击能力，实现传感器结构的强壮型设计。

将Al2O3陶瓷基板设计成冗余结构并制成单片集成的4单元阵列结构，采用“三明治”结构。在感温点表面进行介质薄膜化物理隔离保护，解决热电偶敏感膜遇金属粒子污染变性问题。将“三明治”结构组装到防护陶瓷管内，最后组装到带孔的滞止罩内，传感器结构图如图1所示。

图1 传感器整体结构

2 流热耦合分析

流热耦合传热是研究物体在流场作用下的传热过程以及物体传热对流场影响的一个研究领域，涉及流体力学的基本理论、计算流体力学、数值传热学、耦合理论、数值求解方法以及实际应用等多个方面。高温薄膜传感器在测温时，被测气流和高温薄膜传感器的流热耦合传热过程包括:气体的对流换热以及传感器内部导热。

为了提高传感器的响应时间，减小传感器测量误差，本文模拟燃气轮机排气孔的测温过程，利用流热耦合多物理场仿真分析方法对高温薄膜传感器进行数值仿真，根据如图2所示的计算模型计算出传感器进气口面积和出气口位置对传感器响应时间和测量误差的影响情况，进而优化传感器的结构尺寸。

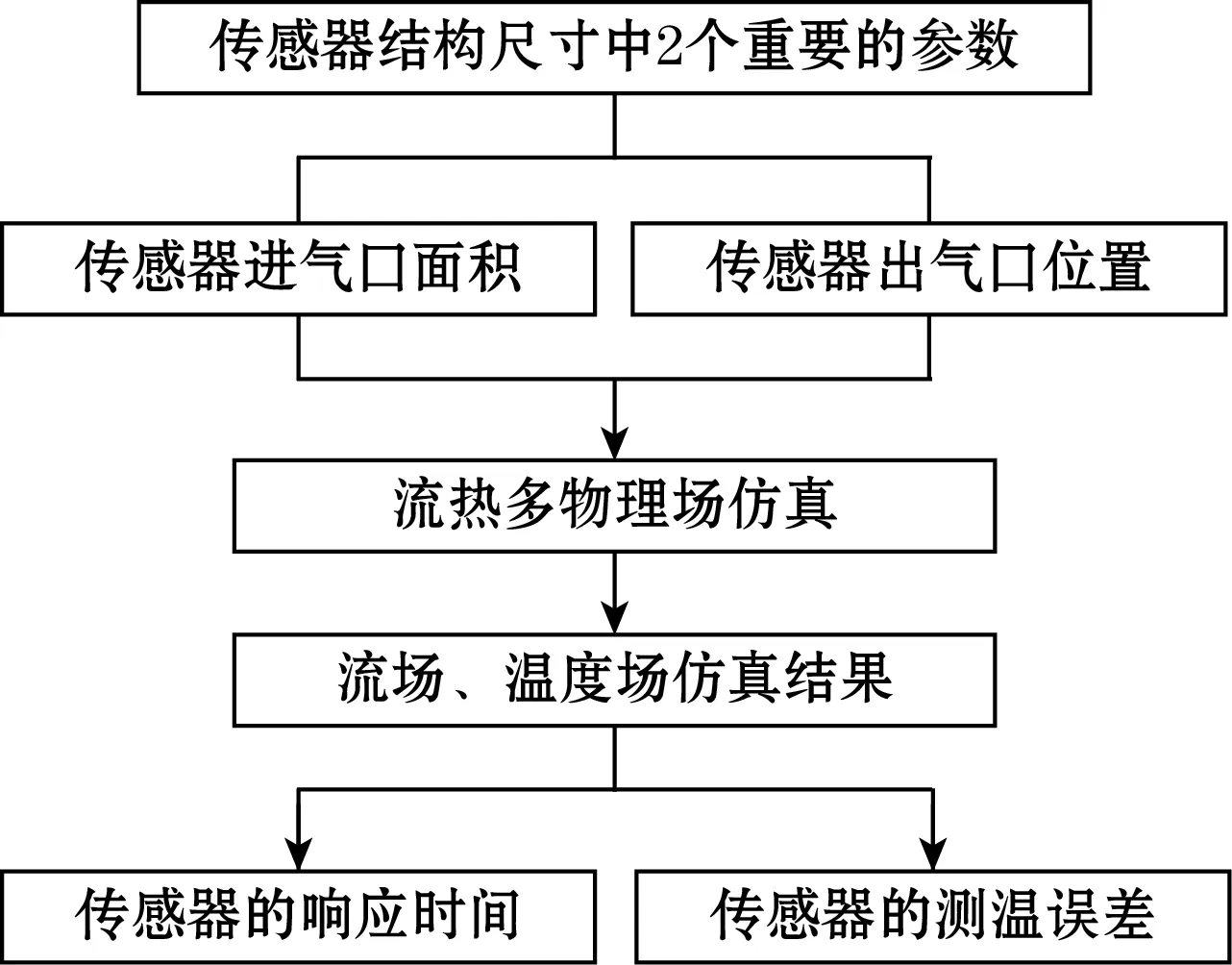
图2 高温薄膜传感流热耦合分析计算模型

2.1 流热耦合传热

流热耦合传热涉及流体力学的基本理论、数值传热学、计算流体力学、数值求解方法、耦合理论、以及实际应用等多个方面。高温薄膜传感器在测温过程中气流通过进气口在腔体实现流热耦合的传热过程包括：对流换热以及传感器内部导热。

高温薄膜传感器的外部不可压空气的流动控制方程为：

▽v=0

(4)

ρv▽v=-▽p+μ▽2v+ρgβ(T-Tf)

(5)

式中：v为速度矢量;ρ、p、μ分别为密度、压力、和动力粘度；g、β分别为重力加速度和空气热膨胀系数；T、Tf分别为传感器表面温度和流体表面温度。

高温薄膜传感器的内部能量方程为

(6)

式中：Cp，λ分别为比热容和导热系数。

高温薄膜传感器的表面换热边界条件为

(7)

式中：γ为高温薄膜传感器表面热流密度；γdn和γco分别为传感器内部热量损失与外界气体对流换热。

2.2 网格划分及仿真分析

本文对高温薄膜传感器及腔体内部的流场区域采用自适应能力较强的非结构化网格划分技术生成网格模型，对尺寸较小的区域及流热耦合界面进行网格加密，进而提高整体的网格质量。选取40～120万网格数量的模型进行网格的无关性检验，用以提高网格的自适应性，结果表明网格数量在60～120万条件下仿真结果差距小于1%，达到网络无关性要求，因此本文采用60万的网格数量进行仿真。图3为计算流热耦合分析的高温薄膜传感器和腔体内部的网格划分，网格的增长率达到1.1，网格质量达到仿真计算的要求。

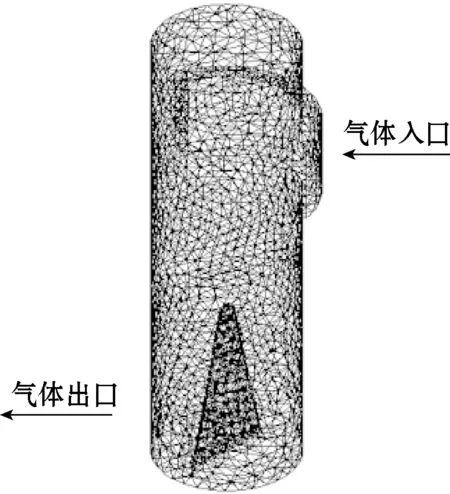
图3 传感器有限元模型及网格划分

模拟高温薄膜传感器对燃气轮机排气温度检测的过程，以480 m/min的速度排放气体，气体由滞止罩的进气口进入并与传感器芯片接触实现热传导，在数值仿真中，定义传感器芯片表面为流热耦合界面，采用湍流模型，这样可以使得计算精度更高且更符合实际应用，流体进口的边界条件设置为速度入口，出口采用压力出口边界条件，气体材料设置为理想不可压缩气体，固体材料定义为Al2O3陶瓷，材料属性见表1，初始化固体温度为300 K，流体温度设置为1 000 K，由于计算涉及对流换热和热传导，故本文采用能量方程，求解器采用耦合隐式求解器，这样可以最大程度的提高计算精度和收敛性，最后将流场仿真结果导入瞬态温度场模块计算传感器的响应时间。

表1 材料属性

从图4高温薄膜传感器芯片的温度分布云图中可以看出，由于流体温度的影响，高温薄膜传感器的温度由传感器芯片的顶端向底端递减，符合传热物理规律，通过温度分布云图也可以证明传感器感温节点设计的正确性，因此本文传感器的响应时间均取自该点温度。

图4 Al2O3陶瓷基板的温度分布云图

3 结果分析

图5为仿真过程中传感器的温度变化的情况，在仿真的前10 min中传感器处于未工作状态，温度为仿真所设置的室温300 K，从第10 min开始向传感器中通入480 m/min的气体，气体温度设置为1 000 K，传感器的感温节点处的温度随着时间的增大而增大，待传感器温度稳定5 min后，撤去气体传感器自然冷却，最终在35 min时基本稳定在室温，由图5可知，在10 min通入气体后传感器的温度值快速上升，平均升温速率为159.6 K/min，最大升温速率为210.2 K/min。

图5 传感器的测温曲线

3.1 响应时间分析

为了更好的探究传感器结构尺寸对传感器响应时间的影响，通过仿真模拟传感器的整个测温过程，建立传感器进气口面积为10 mm2、20 mm2、30 mm2、40 mm2、50 mm2的传感器模型，出气口位置距离传感器芯片底部高度为3 mm、8 mm、13 mm、18 mm、23 mm，并对传感器模型进行流热耦合多物理场仿真分析，仿真结果如图6所示，从图6中的数据可知，传感器的响应时间随着进气口面积的增大而加快，随着出气口位置的升高而减慢，但明显进气口面积对传感器的响应时间影响更为显著，图7为不同传感器结构尺寸与响应时间的关系。

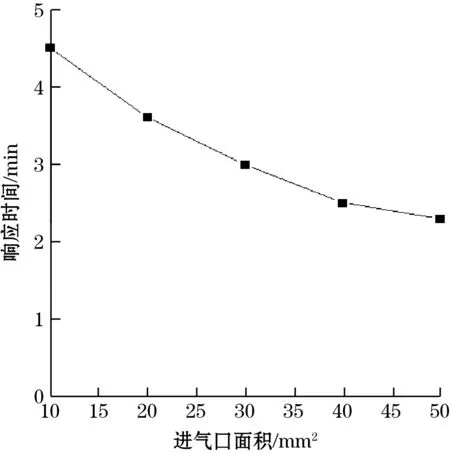
(a)传感器进气口面积对响应时间的影响

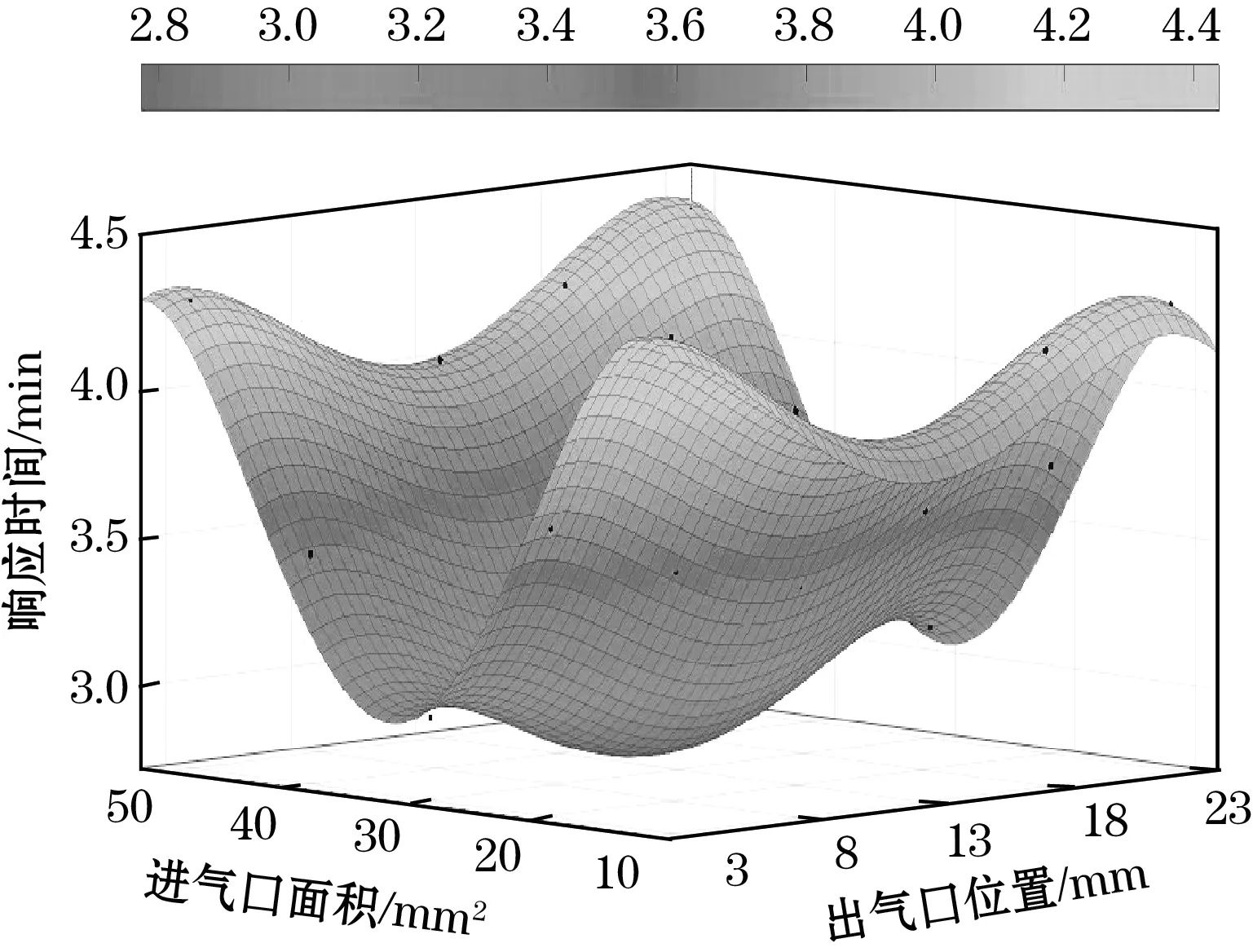
图7 不同结构尺寸与响应时间的关系

3.2 传感器误差分析

传感器测温的有效性和准确性是传感器工作的重要指标，传感器的结构尺寸不但影响传感器的响应时间还对传感器的测量误差有重要的影响，为了揭示传感器结构尺寸对传感器测量误差的影响，在上述流热耦合的基础上分析传感器的绝对误差，将达到稳定时的仿真结果与输入的气体温度进行对比，由图8可知，随着传感器开口面积和出气口位置增大传感器绝对误差也增大，最大绝对误差为7.4 K。图9为不同传感器结构尺寸与测量误差的关系。

(a)传感器进气口面积对传感器误差的影响

4 传感器的结构优化

由于流热耦合计算方法只能计算有限个离散模型，如果可以计算出任意进气口面积和出气口位置条件下的流热耦合仿真结果，就能求解出响应时间最快、测量误差最小的传感器结构参数。粒子群算法是一种基于群体协作的随机搜索算法，该算法能快速寻求全局最优解而不需要任何初始化信息。采用粒子群算法对图7中高温薄膜传感器的仿真结果进行公式拟合，获得响应时间T与进气口面积x和出气口位置y之间的关系方程(8)，同样对图9中的仿真结果进行拟合，获得传感器测量误差C与进气口面积x和出气口位置y之间的关系方程(9)。

图9 不同结构尺寸与测量误差的关系

T=w1+w2x+w3y+w4x2+w5xy+w6y2

(8)

式中：w1=5.911；w2=-0.162 1；w3=-0.059 62；w4=0.002 445；w5=0.000 162 1；w6=0.002 47。

(9)

式中：p1=0.898 9；p2=0.045 65；p3=-0.085 37；p4=0.000 234 2；p5=0.001 576；p6=0.009 509；p7=0.006 188；p8=-0.010 08。

为了验证拟合计算结果的可信性，选取图7曲面中未用于方程拟合的9个点进行仿真计算，并将仿真结果与拟合方程计算结果进行对比。选取进气口面积x为15 mm2，25 mm2，35 mm2，出气口位置y为5 mm，10 mm，15 mm，获得的仿真结果为T1，将数值带入拟合方程得到计算结果为T2。将2组结果进行对比如表2所示。

表2 响应时间的仿真值与方程计算值对比

根据表2中仿真数值和方程计算结果可以得出，响应时间的平均绝对误差和均方根误差分别为0.015 s和0.019 s，表明方程拟合精度较高，求解最佳的传感器结构参数，不仅要求解目标函数式(8)的最小值，还要将传感器误差曲线拟合出的式(9)作为约束条件加以限制，最终得出传感器结构的最佳参数为进气口面积32.686 mm2，出气口位置9.798 mm，代入方程(9)中得到此时的传感器误差为2.9202 K，满足传感器精度要求[12]。

5 结论

本文提出了一种高温薄膜快响应传感器，采用流热耦合分析方法从进气口面积和出气口尺寸2个方面对高温薄膜传感器的响应时和测量误差进行了数值分析，结果表明，进气口面积和出气口位置与传感器响应时间均成正相关，但进气口面积影响较为显著，同时进气口面积与出气口尺寸也影响传感器的测量误差，进气口面积对测量误差影响较小，出气口位置在0～10 mm时对传感器测量精度影响较小，大于10 mm时，随着出气口位置的上升，传感器的测量误差急剧增大，通过粒子群算法拟合仿真数据，获得不同进气口面积和出气口位置条件下的计算结果方程，并与仿真结果进行对比，提高流热耦合仿真方法的普适性，通过方程计算出高温薄膜传感器的最佳结构尺寸。