硅微半球陀螺频率裂解修调工艺规律仿真分析

胡友旺， 钟宏民，孙小燕，段吉安，庄须叶

(1.高性能复杂制造国家重点实验室，中南大学机电工程学院，湖南长沙 410083；2.华东光电集成器件研究所，安徽蚌埠 233042)

0 引言

陀螺仪是测量角速度或角位移的传感器[1]。硅微半球谐振陀螺仪不仅具有传统半球形谐振陀螺仪结构对称性好、抗干扰、可靠性高等优点，还具有微机电系统陀螺仪体积小、功耗低、成本低等优点，同时与传统半导体加工工艺兼容性好，易批量化生产，是最具发展潜力的新型陀螺仪之一[2-3]。

频率裂解是影响陀螺性能的主要缺陷之一，它会影响陀螺的灵敏度、分辨率等重要性能指标[4]。频率裂解主要由谐振子的结构不对称、材料、应力的不均匀性等原因导致[5]。由于制造误差的存在，导致频率裂解不可避免的存在。对于未经过任何修调处理的微半球谐振子，其频率裂解大多在10 Hz以上，尤其是对于批量制造的谐振子来说，很难一致地保证所有的谐振子的频率裂解都保持在较小的值[6-7]。因此，通过后续的修调来降低频率裂解是很有意义的。

对于硅微半球陀螺来说，由于其尺寸小(厚度在μm量级，直径在mm量级)，故其模态频率对于各工艺参数都非常敏感，很小的加工量或加工误差也会造成较大的频率波动，使得修调后的频率裂解实际值与期望值相差较大。所以，为了尽可能降低硅微半球陀螺的频率裂解，需要高精度的修调方法以及合适的工艺参数，以降低各种不确定因素所引起的频率波动，使修调效果稳定。

为确定合适的修调方法和工艺参数，本文针对一种带有矩形质量块的硅微半球陀螺，采用在其质量块上进行打孔的修调方法，并利用有限元软件分析了修形孔的不同位置、不同孔径、孔深，对频率裂解的影响规律，为硅微半球陀螺的频率裂解修调实验提供参考。

1 基本工作原理

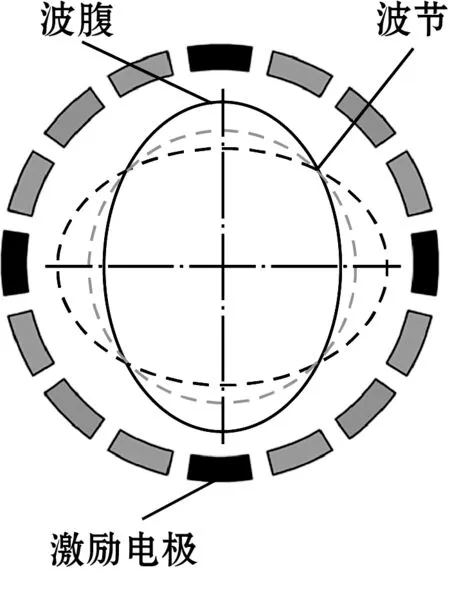
硅微半球陀螺作为一种哥氏振动陀螺，工作在四波腹四波节的模态下[8]。如图1所示，陀螺工作时，由激励电极激励出谐振子的初始振型，当陀螺存在角速度输入时，由于哥氏力的存在，振型发生环向的进动，进动的速率和输入角速度成正比[9]。由检测电极检测出此进动角，即可解算出陀螺的旋转角度和角速度。

(a)初始振型

对于理想的谐振子，任意环向偏角下的振型固有频率相等。但由于制造误差等因素导致谐振子质量、刚度分布不均匀的偏差，偏差的四次谐波导致2个互45°角的固有轴系，称为刚性轴，振型在这2个固有轴系下的频率分别达到最大值和最小值，它们的频率差即为频率裂解[10]。

2 有限元模型

本文所分析的硅微半球陀螺使用材料为多晶硅，密度2 330 kg/m3，杨氏模量160 GPa，泊松比0.23。谐振子模型是一个厚度均匀的半球壳，顶部均布16个矩形质量块。模型如图 2所示，(图2中R=600 μm，H=305 μm，ra=110 μm，rc=160 μm，ha=5 μm，t=2 μm，φm=11.25°，wm=40 μm)，网格采用20节点的六面体单元，通常，同样的网格尺寸下，六面体网格比四面体网格质量较高，数量少，计算时间较短[11]。对于理想的模型，仿真得到的频率裂解为4.2×10-4Hz(其中，模态A：15 075.634 29 Hz，模态B：15 075.633 87 Hz)。

图2 模型与尺寸

频率裂解的修调通常在2个刚性轴方向进行，通过改变刚性轴0°及90°方向上的等效刚度或质量可以改变频率裂解，其原理可用式(1)简要表示[12]：

(1)

式中：ω′为修调后的谐振子的固有频率；k*为修调前谐振子的等效刚度；Δk为修调引起的等效刚度的减小；m*为修调前谐振子的等效质量；Δm为修调引起的等效质量的减小。

通过在谐振子唇边加工微孔、微槽，去除微小的质量是某些结构的MEMS陀螺常用的频率裂解修调方法之一[6，13]。为了简化计算，使用矩形微孔来量化此方法所加工的微孔或微槽，如图 3所示。在频率的修调前，会将刚性轴与电极对齐，而每个电极与一个矩形质量块对齐。故频率修调时，为了保证刚性轴环向偏角不变，只需在某一个刚性轴对应的质量块上加工出对称的4个孔即可，如图3所示。孔的周向位置位于质量块的中间，其径向位置通过其中心与壳体内壁的距离d来表示，通过改变不同的孔径、孔深和孔的径向位置可以适用于不同大小的频率裂解。

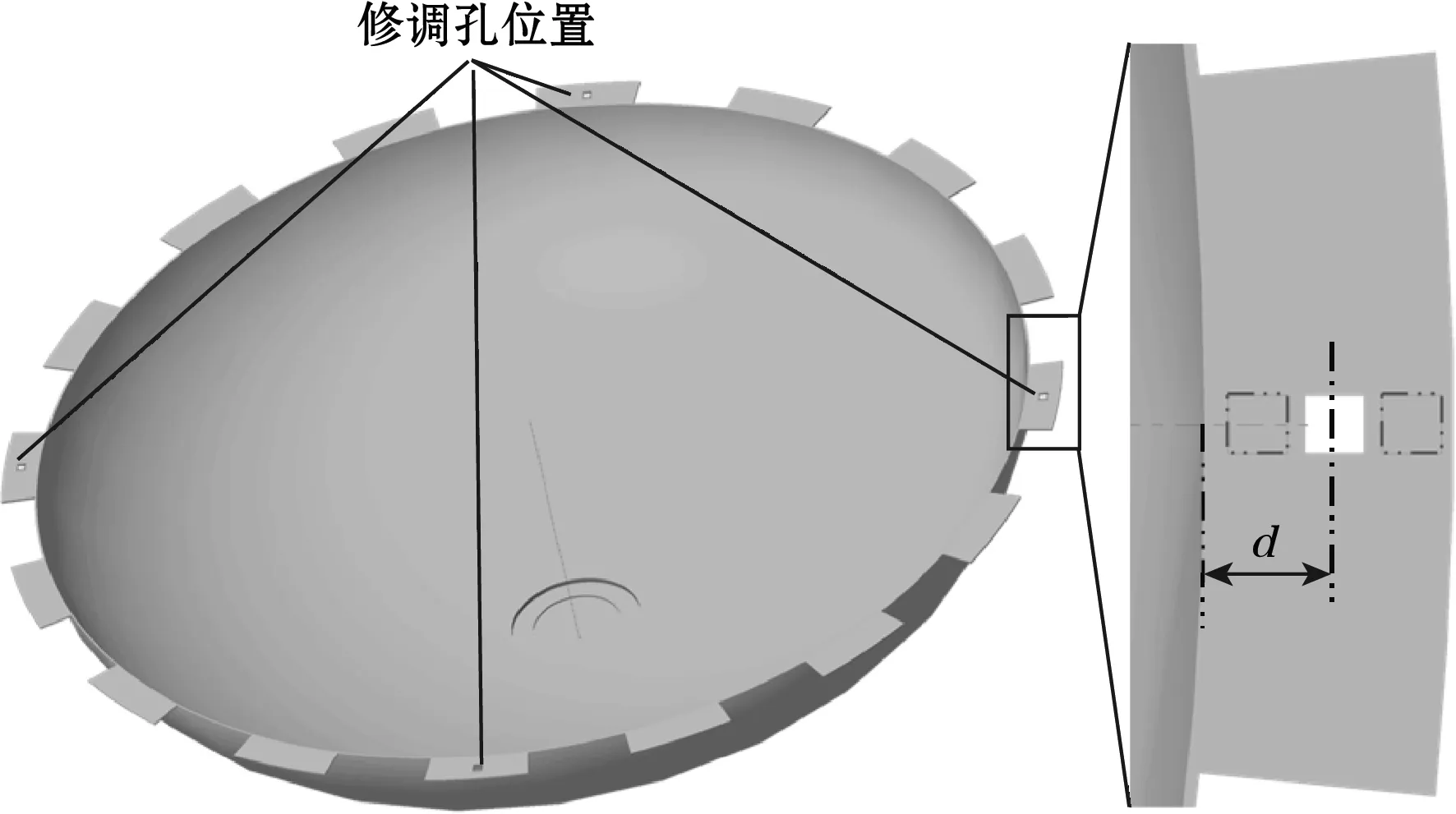
图3 修调孔位置

3 工艺规律仿真分析

3.1 孔径对频率裂解的影响

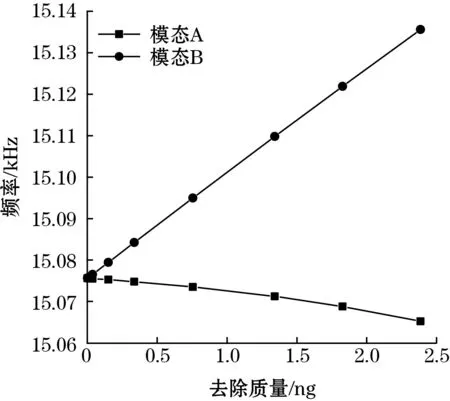
首先，为了研究修调孔的孔径对频率及频率裂解的影响，设置如下实验：孔深为常数1 μm，孔边长由1～32 μm逐渐变大，位于模态B方向上的质量块的中间。得到的仿真结果如图4所示。

如图4(a)所示，随着孔径的变大，孔的去除质量逐渐增加，模态B(修调孔对应方向)的频率逐渐上升，而模态A频率逐渐下降，并且模态A的频率变化量远小于模态B。这导致了频率裂解逐渐增加，并且，频率裂解的变化与修调孔的去除质量有着较好的线性关系，如图4(b)所示。所以，实际修调过程中，应在低频模态上打孔以增大低频模态的频率同时减小高频模态的频率，来减小频率裂解。

(a)孔边长对模态频率的影响规律

由式(1)可知，模态方向上的等效刚度减小时，模态频率将下降，而等效质量减小时，模态频率将上升。这说明修调孔对于修调轴来说，质量变化是影响频率的主要因素，而对于未修调轴，刚度变化是影响频率主要因素。

随着孔尺寸的变化，频率裂解的变化范围是0.067 9～70.412 7 Hz，这说明了打孔式修调方法的有效性。同时，孔径只在μm尺度上变化，频率裂解就已经有较大的改变，陀螺的频率裂解对于孔径的变化较敏感，需要很高的修调加工精度。为了衡量频率裂解对于加工参数的敏感程度，本文给出一个衡量频率裂解修调效果的物理参数，修调效率η，即：单位去除质量带来的频率裂解变化量，可以用式(2)表示：

(2)

式中：η为修调效率，Hz/ng；Δf为修调前后频率裂解的变化量；m为修调孔的质量，ng。

对图4(b)中的数据线性拟合得到其频率裂解修调效率为29.31 Hz/ng。若要使得频率裂解变化0.1 Hz，则由式(2)可得孔的去除质量为0.1/29.31=3.412×10-3ng，对应体积则为1.464 μm3，加工精度需要达到μm级，而若要使得频率裂解降至0.01 Hz以下，则修调的加工误差不能超过0.146 4 μm3，这需要非常精密的修调方法。

3.2 孔深对频率裂解的影响

为进一步研究孔深对频率裂解及修调效率的影响，现进行以下仿真实验：孔边长8 μm × 8 μm并保持不变，孔深逐渐增加，位于模态B方向上的质量块的中间。其仿真结果如图5所示。

(a)孔深对模态频率的影响规律

由图5(a)可知，与只增加孔径的情况类似，随着孔深的增加，孔的去除质量逐渐增大，模态B的频率逐渐上升，而模态A的频率基本不变，这使得频率裂解的变化逐渐增加，如图5(b)所示。对图5(b)中的数据进行线性拟合得到这种情况下的频率裂解修调效率为25.76 Hz/ng，略小于上一节中的增大孔径的情况，但依然比较大，频率裂解对于孔深的变化也很敏感。

修调效率的大小体现出陀螺的频率裂解对于该参数的敏感程度，效率越大，则频率对于该参数的变化越敏感，加工难度也越大。所以对于较小的频率裂解修调需求，较小的修调效率对于减小加工难度是有利的。由于只增加孔深时的修调效率小于增加孔径的方法，所以对于小的频率裂解修调，应优先考虑增加孔深来达到修调需要。

3.3 孔的深宽比对频率裂解的影响

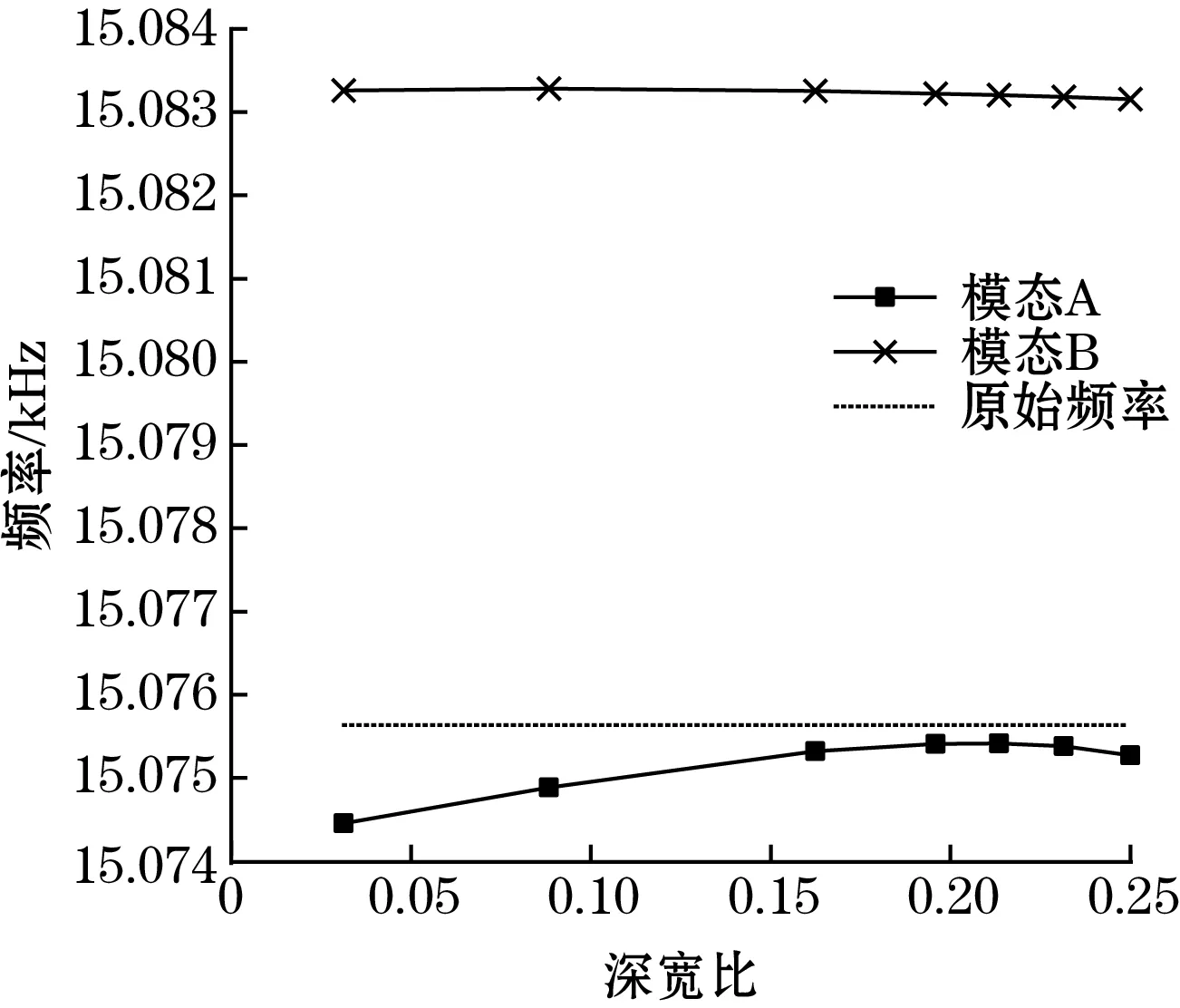
为了进一步研究修调孔的不同孔径及孔深对频率裂解的影响，进行以下仿真实验：孔的体积始终为128 μm3，孔的深宽比(孔深度/孔边长)逐渐增加，位于模态B方向上的质量块的中间，具体实验参数如表1所示。仿真结果如图6所示。

表1 实验参数

(a)频率

由图6(b)可见，虽然孔的去除质量相同，但其深度、宽度不同时，对频率裂解的影响也不尽相同，孔深在1.8 μm时，频率裂解达到最小值7.81 Hz，频率裂解的最大值为8.81 Hz，变化幅度在12.8%左右，修调效率在26～30 Hz/ng之间。

图6(a)中，模态B(修调轴)的频率始终大于初始频率，而模态A的频率始终小于初始频率。由式(1)可知，模态B方向上等效质量的减小使得其频率的增加，而模态A方向上等效刚度的减小导致了模态A频率的减小。随着深宽比的增大，模态B的频率略有下降，但相对于模态A变化幅度很小。这说明孔深宽比增大过程中，由于孔的去除质量保持不变使得模态B方向上的等效质量基本不变，孔的结构上的改变引起了模态A方向上等效刚度的变化，所以模态A的变化幅度大于模态B。所以孔去除质量不变，深度、宽度改变时，刚度的变化是造成图6中频率裂解不同的主要原因。

随着深宽比的增大，孔深逐渐增大而孔边长逐渐减小，使得模态A的频率逐渐增加，频率裂解逐渐减小，说明孔宽度的减小使得修调孔对等效刚度的影响(即式(1)中的Δk)减小。而在质量块即将被孔打穿时，由于质量块结构上的破坏使得Δk的增大，使得等效刚度的减小，从而使得模态A的频率下降以及频率裂解的上升。但由于上升幅度较小，所以基本上可以认为大深宽比的孔的修调效率较小，对于较小的频率裂解修调需求，应使用深宽比较大的修调孔。

3.4 孔的径向位置对频率裂解的影响

为了研究修调孔的不同位置对频率裂解的影响，进行以下仿真实验：孔的体积始终为8 μm3，按孔深分为不同的5组：0.5 μm，1 μm，1.5 μm，1.8 μm，2 μm，每一组孔的径向位置从里向外移动。仿真结果如图7所示。

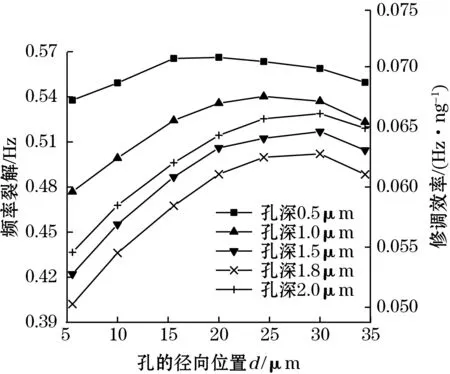
图7 孔的径向位置对修调效率的影响规律

如图7所示，体积相同情况下，随着孔的深度、宽度和径向位置的不同，所引起的频率裂解变化不同，频率裂解在0.40～0.57 Hz之间，修调效率大约在21～30 Hz/ng之间，变化幅度在40%左右。另外，深度为1.8 μm的孔，其频率裂解及修调效率始终小于其他深度的孔，这与上一节的结果相似。

孔的径向位置从里向外移动时，其频率裂解和修调效率先增大后减小，但频率裂解和修调效率的最小值始终在靠近球壳处。所以，对于小的频率解裂，可以靠近陀螺内侧打孔修调，以使得同样的频率裂解下去除的质量更多，加工较容易；对于大的频率裂解，可以靠近外侧打孔修调，以使更小的去除质量就能达到修调要求，修调效率更高。

4 结束语

硅微半球陀螺小而脆弱的谐振子导致修调难度大，为确定需要合适的修调方法和工艺参数，本文介绍了硅微半球陀螺频率裂解微孔修调方法。并通过仿真分析了其工艺参数对频率裂解的影响规律。

结果表明应该在低频模态上打孔以减小频率裂解。该方法下每去除1 ng质量改变的频率裂解在21～30 Hz/ng之间。频率裂解对于各工艺参数变化较敏感，若要使得频率裂解减小到理想值，修调的加工精度需要在微米级甚至是亚微米级。

当需要修调的频率裂解较小时，即修调孔的体积较小时，应优先使用深宽比较大的孔，并且孔的位置应尽量靠近内壁。对于大的频率裂解，可以靠近外侧打孔修调，以使更小的去除质量就能达到修调要求，修调效率更高。