柱脚铰接的常规多层钢框架静动力分析

虞爱平， 章艺耀， 王翠红， 尹 霞， 包恩和

(广西建筑新能源与节能重点实验室, 桂林 541004)

为实现强震作用时钢框架结构能够形成整体破坏机制，各国抗震规范出台了关于钢框架结构强柱系数的相关规定。中国的《建筑设计抗震规范》(GB 50011—2010)[1]和美国钢铁结构协会(American Institute of Steel Construction，AISC)SpecificationsforStructuralSteelBuildings[2]都按钢框架柱梁节点设计强柱系数，其中中国规定结构抗震等级一级、二级和三级时对应的节点强柱系数分别是1.15、1.10和1.05；美国规定H型钢柱抵抗弯矩大的强轴方向上的节点强柱系数大于1.1；与中美规范不同，日本规范[3]中强柱系数按结构层设计，规定结构层的强柱系数要求大于1.5。

中外学者对于取不同的强柱系数，对强震作用下的钢框架结构破坏机制产生何种影响展开了一系列研究。基于简化结构体系，综合评价超强柱弱梁型钢框架结构体系的抗震效果[4-5]；研究实现钢框架整体机制时地震输入能量与结构强柱系数之间的关系[6-7]。基于静力非线性分析的结构顶层位移与首层剪力关系，研究强柱弱梁型钢框架结构的地震响应修正系数[8-9]。以结构形式、柱脚形式及强柱系数等为研究参量，研究常规低层钢框架结构动力损伤分布机理[10-12]。对柱脚刚接的强柱弱梁型多高层钢框架进行弹塑性分析，研究结构静力和动力的层间位移角之间的关系[13]。然而值得注意的是少有常规多层钢框架结构抗震性能方面的相关报道。

基于以上，为研究常规多层钢框架抗震性能，以及根据多层钢框架结构的特点：首层层高大于其他层层高；柱截面沿层高每3层左右一变；柱通过垫板和螺栓与基础连接，柱脚一般按铰接计算。现以强柱系数的不同设计方式(层设计、柱梁节点设计)和强柱系数的大小为主要研究参量，建立柱脚铰接的6个常规多层钢框架结构模型。每个模型的柱脚按铰接考虑、首层层高均大于其他层层高以及柱截面沿层高每3层左右一变；运用平面框架组合非线性分析(combined non-linear analysis for plane frame，CLAP)平台对模型进行弹塑性静动力分析，以研究其抗震性能。

1 分析模型

1.1 模型结构方案

钢框架模型采用规则的三跨四榀结构，总层数为8层。模型的平立面构件布置如图1所示；因此结构不考虑扭转作用的影响，则采用图1(b)所示的刚性梁铰接Y0框架与Y1框架的平面结构模型计算。模型的柱脚采用铰接，梁柱节点采用刚接；模型每榀跨度为7.2 m，首层和2～8层层高为4.5、4 m，楼层总高为32.5 m；首层、2～7层、8层的竖向荷载分别为3 554、3 477、3 342 kN。模型柱、梁分别采用矩形截面型钢、H型钢，选用Q355级钢材。模型的梁和柱共同承受水平、竖向荷载，损伤分散于结构各层各构件，其普遍应用于中国、日本、韩国等。

G1为Y0榀框架中跨梁；iG1为第i层Y0榀框架中跨梁；C2为角柱；C2-1为一角柱编号图1 模型平立面构件布置Fig.1 Floor plan and elevation of prototype building and component configuration

1.2 模型命名

依据模型的强柱系数的定义和结构1～7层的强柱系数大小以命名模型，并用M-①～M-⑥表示，其中层用f表示、节点用j表示，如表1所示。

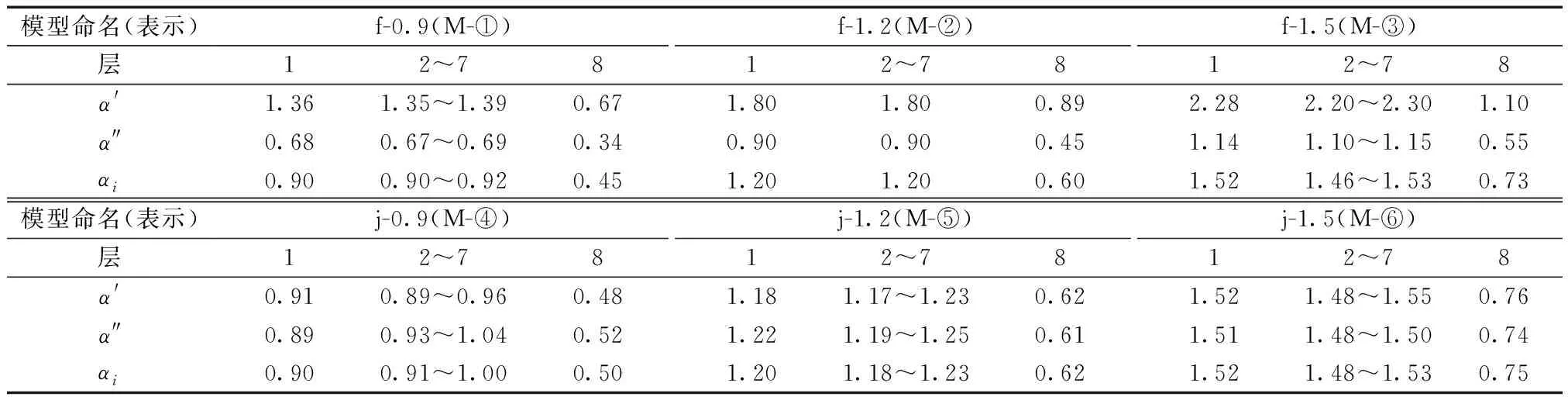
表1 各模型命名及强柱系数Table 1 Model name and the strong column coefficient

1.3 模型的首层剪重比和强柱系数

首层剪重比(CB)计算公式为

CB=Vu1/W

(1)

式(1)中：Vu1为模型弹塑性极限状态下的首层剪力；W为模型的总重量。

强柱系数α按不同定义建立分析模型，其中按照节点定义模型边柱强柱系数(α′i)和中柱强柱系数(α″i)时的计算简图，如图2所示。

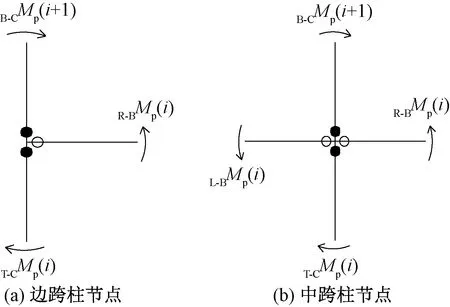
B-CMp(i+1)为第i+1层柱底的全截面塑性弯矩；T-CMp(i)为第i层柱顶的全截面塑性弯矩；L-BMp(i)为第i层梁左端的全截面塑性弯矩；R-BMp(i)为第i层梁右端的全截面塑性弯矩图2 强柱系数的节点计算简图Fig.2 Joint calculation diagram of the strong column coefficient

由地震输入能量与结构的重量W和基本周期T有关，模型的W相同及T相近，说明输入各模型的地震能量相同，另外模型T1为1.7～1.9 s，故以α的大小及其定义形式作为主要研究参量，分析模型的损伤分布规律。

模型M-①～M-③按层定义α，第i层的强柱系数αi[14]按层定义的计算公式为

(2)

式(2)中：累加范围为第i层所有梁、柱的全截面塑性弯矩。

模型M-④～M-⑥按节点定义α，α′i和α″i计算公式为

(3)

(4)

各模型的首层剪重比CB=0.25，模型1～7层的αi基本一致，另外模型M-④～M-⑥的α′i和α″i相同，模型M-①、M-②和M-③的αi依次为0.9、1.2、1.5；模型M-④、M-⑤、M-⑥的α′i和α″i依次为0.9、1.2、1.5。

一般情况下，低多层钢结构框架首层柱底端与基础通过锚栓和垫板连接，设计中按铰接简化计算；因此，各模型的柱脚形式按铰接考虑。

2 静力分析

2.1 分析方法

各模型的计算模型按照图1(b)所示，在静力推覆分析过程中的荷载布置为：竖向荷载集中作用于每层柱顶及梁跨中；根据拟静力法得到的地震水平等效力作用于各层柱顶。竖向荷载布置如图3所示。通过CLAP平台[15]对各模型进行二阶非线性位移增份分析，计算100增份，每增份的顶层位移Δ=7 mm。同时，假设构件材料屈服后的刚度为初始刚度的 1/100。

图3 模型的竖向荷载布置Fig.3 Vertical load arrangement of each model

2.2 层剪力与层间位移的关系及塑性铰的形成情况

图4分别表示M-②、M-③、M-⑤及M-⑥模型的层剪力(V)与层间位移(Δ)关系及Y1榀框架塑性铰的形成情况，并在各模型的层剪力和层间位移曲线图中绘出达到弹性层间位移角限值1/250和弹塑性层间位移角限值1/50时各层剪力与位移关系曲线。图4中塑性铰分布图中梁柱节点及支座处数字为增份的次数。由图4可知，因柱脚铰接，首层反弯点移至柱脚处，首层柱计算长度增大，首层柱线刚度减小，首层刚度也减小；而结构变形向首层集中。

图4 模型M-②～M-⑥层剪力与层间位移的关系及塑性铰形成情况Fig.4 Story-shear-force to inter-story displacement relationship and its plastic hinge mechanism of the model M-②～M-⑥

强柱系数为1.2的M-②、M-⑤模型，强柱系数按层定义的M-②模型的塑性铰主要分布于中柱和边跨梁端部，边柱基本保持弹性，没形成结构局部破坏机制；而强柱系数按节点定义的M-⑤模型的塑性铰主要分布于1～3层柱梁端部，首层形成结构局部破坏机制。

强柱系数为1.5的M-③、M-⑥模型，强柱系数按层定义的M-③模型的塑性铰主要分布于1～6层中柱端部和梁端部，边柱保持弹性；强柱系数按节点定义的M-⑥模型的塑性铰主要分布于1～6层梁端部，柱基本保持弹性状态；模型M-③、M-⑥的结构均形成整体破坏机制。

3 动力分析

3.1 分析方法

假定构件的恢复力模型是双线型，屈服后刚度为初始刚度的1/100，框架阻尼矩阵为阻尼系数2%的刚度比例型。分析模型、分析平台和竖向荷载布置同2.1节。

地震波选用1995年日本阪神地震人工波(JMA Kobe Art，JKA)、1995年日本阪神地震天然波(JMA Kobe NS，JKN)和1952年美国加利福尼亚州地震天然波(Taft EW，TE)。按不同的地动最大速度值将地震波强度等级分为两个等级：地动最大速度值为50 cm/s对应设防烈度地震(等级2)，分别用JKA-2、JKN-2、TE-2表示；地动最大速度值为75 cm/s对应罕遇地震(等级3)，分别用JKA-3、JKN-3、TE-3表示。具体如表2所示。

表2 模型分析用地震波的详情Table 2 Details ofearthquake wave parameters of each model

在JKA-2、JKN-2、TE-2地震波作用下，等效速度-周期关系曲线(阻尼比h=0.02)及M-①～M-⑥模型的第一周期(T1)、第二周期(T2)范围，如图5所示。

由图5可知，JKA波和TE波在M-①～M-⑥模型的T1范围时的等效速度值比在T2范围时等效速度值大，可知在JKA波和TE波作用下，结构地震响应主要由第一振型控制；而JKN波的等效速度在T2范围时比在T1范围时稍大，说明JKN波作用下结构第一、第二振型同时影响结构的地震响应。

图5 地震波的等效速度-周期关系曲线Fig.5 Equivalent velocity-fundamental period curves of earthquake waves

3.2 分析结果

3.2.1 层间位移角关系

在两种等级的6条地震波作用下，各模型各层最大层间位移角(θ)的关系曲线如图6(a)～图6(f)，图中加入1/100和1/50的层间位移角作为参考线。

分析图6(a)～图6(c)，在设防烈度地震作用下，各模型的最大层间位移角基本在位移角1/100～1/50，其中首层位移角和6层层间位移角相对大，整体分布较均匀；模型的首层位移角有随强柱系数降低而增大的趋势，另外，按节点设计强柱系数的模型首层位移角大。

参考图5可知，JKA、TE波作用时，结构第一振型的影响突出，而JKN波作用时，结构第二振型响应反而相对明显。因此在图6(d)～图6(f)中得到，在JKA-3、TE-3波作用下，各模型的最大层间位移角出现在首层；而在JKN-3波作用下，各模型的最大层间位移角则出现在6层。各模型变形有随强柱系数减小向首层集中的趋势；同时，M-④～M-⑤模型的首层位移角明显比其他模型的首层位移角大，即强柱系数按结构柱梁节点设计的模型首层位移角相对更大。

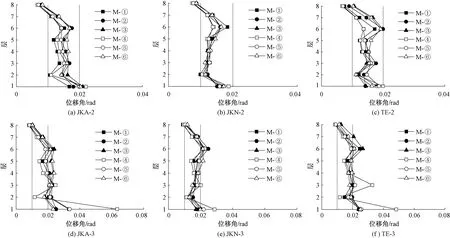
图6 各模型最大层间位移角分布Fig.6 Maximum inter-story displacement angle distribution of each floor for analysis model

在多层钢框架结构中，当强柱系数≤1.2时，按层设计可使变形向首层集中的趋势得到缓和；当强柱系数≥1.5时，按不同设计方式对其最大层间位移角影响不明显；这与静力弹塑性分析结果较好吻合。

3.2.2 最大层间位移角的集中率

最大层间位移角集中率(dR)的计算公式为

dR=θmax/θave

(4)

式(4)中：θmax为模型各层最大层间位移角；θave为建筑物顶部位移与建筑高度之比。

在等级3的3条地震波作用下，M-①～M-⑥的各层最大层间位移角的最大值对应各模型的dR，如图7所示。

分析图7，模型M-①～M-⑥的dR值随着强柱系数的增大(从0.9增大至1.5)而减小；按层设计的模型M-①～M-③的强柱系数依次为0.9、1.2、1.5，其dR从1.7减小至1.3左右，其中模型M-②和M-③的dR接近。按节点设计的模型M-④～ M-⑥的强柱系数依次为0.9、1.2、1.5，其dR从2.9减小至1.35左右；其中模型M-⑤和M-①的dR接近，模型M-⑥的dR与模型M-②～ M-③接近。表明，强柱系数≤1.2时，多层钢框架结构的强柱系数按层设计可缓和变形集中状况。

图7 各模型的dRFig.7 ThedRvalue of each model

3.2.3 各层柱梁的塑性变形能量需求性能

在等级3地震波作用下，各模型各层柱梁最大塑性变形能量(Ep)总合值的各层分布情况，如图8所示。

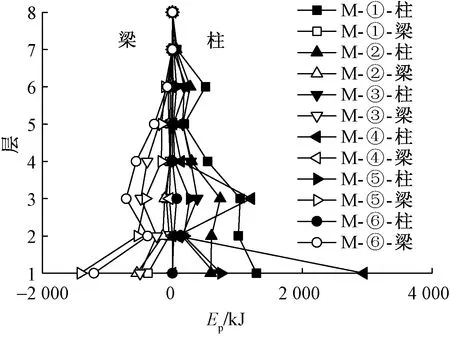
图8 各模型各层柱梁最大塑性变形能量的总合Fig.8 The total maximum plastic deformation energy of beams and columns of each floor for analysis models

由图8可知，模型M-①～M-⑥的Ep主要集中首层的柱和梁，首层的Ep越大，2层的Ep越小，其中模型M-④～M-⑥的Ep集中于首层柱端的现象尤为明显。模型M-①～M-⑥首层柱的Ep值随强柱系数减小而增大，在3～6层梁端的Ep随强柱系数的增大而增大，柱端的Ep随强柱系数的增大而递减，而7、8层则保持弹性状态。另外模型M-③和M-⑥的强柱系数均为1.5，Ep都基本分布在梁端。

由图8可知，各模型的各层柱梁Ep的总合值在结构1～3层相对大。图9所示为M-①～M-③和M-⑤的1～3层的柱端、梁端及柱脚处Ep分布和各模型的Ep最大处(框内)的滞回曲线(除柱脚)。

图9 模型M-①～M-③、M-⑤的1～3层塑性变形能量分布Fig.9 The plastic deformation energy distribution of 1 to 3 layers of the model M-①～M-③ and M-⑤

由图9可知，强柱系数为0.9(按层设计)的模型M-①，形成首层层破坏的局部机制；同时，模型的Ep最大处为首层柱顶。强柱系数为1.3(按层设计)的模型M-②的中柱两端都形成了塑性铰，但边柱始终保持了弹性状态，模型M-②的Ep最大处也是柱端。强柱系数为1.5(按层设计)的模型M-③的塑性铰，基本上分布于梁端，Ep最大处为梁端。强柱系数为1.3(按节点设计)的模型M-⑤，首层柱顶发生塑性变形，首层形成层破坏的局部机制；但M-⑤的Ep最大处也是梁端。

4 结论

(1)静力推覆分析，强柱系数为1.2的模型，按柱梁节点设计时结构形成局部破坏机制，按层设计时结构形成整体破坏机制；而强柱系数为1.5的模型结构均形成整体破坏机制。

(2)强柱系数≤1.2时，多层钢框架结构的强柱系数按层设计可缓和变形向首层集中及减小最大层间位移角集中率；而强柱系数≥1.5时，多层钢框架结构的强柱系数按不同设计方式(层设计、节点设计)，对最大层间位移角和最大层间位移角集中率的影响不大。

(3)结构基本周期与输入地震波等效速度之间对应关系对各模型的最大层间位移角产生影响。

(4)各模型的柱端塑性变形能量随强柱系数增大而减小，梁端塑性变形能量随强柱系数增大而增大；当强柱系数≥1.5时，塑性变形能量基本分布在梁端。