基于磁流变液的球形磁控机器人设计及实验

华德正 刘新华,† 赵欣 路和 李增强 刘晓帆

(1.中国矿业大学 机电工程学院，江苏 徐州 221116；2.姜堰经济开发区科创中心,江苏 泰州 225500；3.中国煤炭教育协会,北京 100713)

随着学科交叉和信息融合，机器人技术不仅广泛应用于制造业、资源勘探、救灾排险、家庭娱乐、军事和航天等领域，在医疗服务方向也取得了较快的发展和显著的成果[1- 3]。近年来，医疗机器人可以辅助医生诊断并开展复杂的手术，具有成功率高、创伤小的优势。然而，人体胃肠道空间狭小且环境复杂，传统医疗机器人的应用受到限制。毫米甚至微米尺度的医疗机器人却可以轻松地在这种空间环境中工作，这将在生物工程和医疗等领域发挥巨大的应用优势[4- 7]。由于这种医疗机器人体型微小，能量的供给成为重要的研究问题[8- 10]。目前，微型机器人的供能分为有缆和无缆两种方式。如果机器人要进入人体器官内作业，有缆供能将会带来极大的不便。因此，无缆供能成为研究的热点。常用的机器人无缆供能方式有静电驱动、电磁驱动、微生物驱动等[11- 14]。其中，外磁场对人体危害较小，且磁控机器人响应迅速，驱动效率高，可以通过改变外界磁场的方向和大小来控制机器人的运动。Bradley J.Nelson及其研究团队多年来一直致力于生物医学领域的磁驱动机器人技术，搭建了基于圆环形电磁线圈的微型机器人驱动系统，能够产生均匀磁场和梯度磁场[15- 18]。通过单独控制线圈上电流的幅值和频率来产生期望的空间磁场，进而完成对钕铁硼材质的微型机器人控制。Shuhei等[19]研发了一种基于折纸方式的机器人，它可以在人体胃部移动，到达期望的位置进行修补伤口、移除异物、运送药物等操作，且机器人本身具有生物相容性和可降解性。Lee等[20]提出了一种用于血管疾病的磁控旋转机器人，主体结构为柱状的永磁体，前后分别安装了柔性的旋转叶片。利用亥姆霍兹线圈产生空间磁场，实现机器人在血管内的精确运动。Guo等[21]研究了多个胶囊机器人模块在狭窄空间内的联合运动模式，通过前后两端的永磁体，这种具有螺旋结构的微型机器人可实现多个模块之间的自动组合运动。Son等[22]研究了一种软体胶囊胃镜机器人，通过尾端增加一种额外的轴向运动，可实现靶向送药和活体采样等医学应用。目前，医疗微型磁控机器人普遍采用磁场强度较高的钕铁硼驱动材料，但是这种永磁体密度大、脆性高，加工制作小体积或者复杂结构时成型困难且容易断裂。本研究采用磁流变液作为机器人的驱动材料，设计一种用于人体胃部靶向送药的球形磁控机器人。针对这种磁控机器人的结构模型，开展了动力学特性分析；通过搭建空间磁场及测试平台，开展速度测试实验，并验证该机器人运动的有效性和可靠性。

1 球形磁控机器人设计

1.1 结构设计

传统的永磁体材料磁化方向恒定、质地坚硬、形状固定；然而，磁流变液作为一种功能材料，常态下为无磁性的胶体，外加磁场时具有固体材料的磁性，且撤销磁场后该磁性消失。如图1(a)所示，本研究设计一种具有矩形空腔的球形磁控机器人，内部填充磁流变液。该球形磁控机器人拥有较强的环境适应能力，可以翻越坡度较小的斜面；同时具有灵活的转弯能力，如图1(c)所示。该机器人的球体直径为4 mm，矩形腔体的长、宽、高分别为2.7、2.0、1.3 mm。

如图1(a)所示，将磁流变液注入该球形磁控机器人的矩形空腔中，外加磁场时，磁流变液的磁性颗粒沿磁场强度H方向瞬间成链，其成链机理会在下一节具体介绍。若球形磁控机器人矩形腔体的长边与磁场方向不一致，则会产生自动的定向运动，使得矩形腔体的长边与磁场方向平行，如图1(b)所示。磁流变液的磁性颗粒沿磁场方向结链时，随着磁场的增强，颗粒链不断强化且与腔体长边的夹角越来越小，最终颗粒链饱和且夹角为零。由于磁性颗粒最终的成链方向与腔体长边趋于平行，所以该球形磁控机器人具有初始的定向运动。当空间磁场开始旋转时，机器人矩形腔内磁流变液的颗粒链与外部磁场方向产生偏差，颗粒链在磁矩作用下转动。进一步地，颗粒链将自身受到的磁矩作用到腔体壁面上，驱动球形壳体跟随磁场的旋转而滚动。因此，该球形磁控机器人通过外部旋转磁场产生的磁矩实现滚动运动，磁场的旋转频率控制该机器人的运动速度，而旋转方向决定机器人的运动方向。另外，该球形磁控机器人在磁场环境中能够被瞬间磁化，在恒定的梯度磁场中同样会受到磁吸引力的作用，保持位置稳定。

图1 球形磁控机器人设计方案及运动示意图

1.2 磁流变液驱动机理

磁流变液是一种形态和性能受外部磁场控制的智能材料,具有高磁导率和低磁滞性[23]。磁流变液主要由磁性颗粒、基载液以及表面活性剂组成[24]，在零磁场时呈现出低黏度的牛顿流体特性；而在强磁场作用下具有高黏度、低流动性的Binghan体特性。如图2所示，磁流变液在磁场作用下的流变效应是毫秒级的、可逆的，磁性粒子的成链情况与磁场强度具有稳定的对应关系。

图2 磁流变液流变效应

从微观角度利用磁畴理论对磁流变液的流变效应加以解释。首先，磁流变液中的磁性颗粒可被划分为众多小型磁化区域，称为磁畴，不同磁畴间的分界面称为磁畴壁。每个磁畴具有自己的磁矩方向，但相邻磁畴的磁矩方向各不相同。因此，各磁畴的磁矩矢量和为零，磁性颗粒总体不显磁性。在磁场作用下，磁性颗粒中各个磁畴的磁矩方向发生偏转并逐渐平行于磁场方向，宏观上对外显磁性。当外界磁场增大时，磁性颗粒受到自身磁矩作用以及颗粒间的磁力作用，形成一条沿磁场方向的颗粒链。若外部磁场开始转动，颗粒链的成链方向也会跟随改变，如图3所示。当外界磁场进一步增大时，颗粒链也会进一步增粗增长直到磁饱和状态。

图3 磁流变液颗粒在磁场环境中的成链示意图

2 球形磁控机器人动力学分析

2.1 球形磁控机器人力学分析

球形磁控机器人的外观结构模型如图4(a)所示，基于以上对磁流变液驱动原理的分析，该球形磁控机器人的力学模型如图4(b)所示。

图4(b)中，FN为表面支持力，f为表面摩擦力，G为重力，δ为滚动摩擦系数，θ为矩形腔体长边与磁场方向的夹角，M为磁流变液的磁化强度，B为空间磁感应强度。当球形磁控机器人处于平衡状态时，其驱动力矩可表示为

图4 球形磁控机器人模型与受力分析

T=fr+δFN

(1)

式中，r为球形磁控机器人的半径。

磁流变液作为磁控机器人的驱动材料，在空间磁场中会受到多种作用力的影响，并共同决定驱动力矩T的变化。外加磁场时，磁流变液内的颗粒被磁化，颗粒之间相互吸引且发生转动和平移运动，进而形成颗粒链。当外部磁场偏转时，磁性颗粒的成链方向将同步趋向磁场方向。磁性颗粒在多种作用力的共同影响下，对机器人矩形腔体的壁面施加均匀的驱动作用，此驱动可以看作磁性颗粒链与基载液粘性阻力的综合作用。其中主要作用力有磁力、排斥力、粘性阻力、布朗力、重力、浮力、范德华力以及磁场和粘性阻力产生的力矩等。

1)磁力

假设磁流变液中磁性颗粒是半径为rk，体积为Vk的均匀球形颗粒。外加磁场强度为H时，磁感应强度B跟随外部磁场强度H的变化规律可用以下式子表述：

B=μ0(M+H)

(2)

(3)

(4)

磁流变液内的磁性颗粒被磁化后，任意颗粒i受到周围颗粒影响的磁力表达式为

(5)

式中，rij为颗粒i和颗粒j中心连线的单位矢量,mir和mjr为颗粒磁矩mi和mj在中心连线rij上的分量。假设θij为外加磁场方向与矢量rij之间的夹角，结合式(2)和(3)，磁力公式可表示为

(6)

式中，z为外加磁场的单位矢量。

2)排斥力

磁流变液中的磁性颗粒被磁化后，处于同一平面且拥有相同磁矩方向的颗粒间同极相斥，周围区域内其他颗粒对磁性颗粒i产生的总排斥力为

(7)

根据式(4)可知，当两个磁性颗粒的中心点无限接近，且相对位置矢量rij方向平行于外部磁场方向时，颗粒间的磁力趋于最大化。假设最大磁力为Fmax，此时rij=2rk，Fmax可表示为

(8)

3)粘性阻力

前文假设磁流变液中磁性颗粒为半径rk的球体，根据Stikes阻力公式计算可得，磁性颗粒i所受到的粘性阻力为

(9)

式中，η为基液的动力黏度,μ为颗粒的速度矢量。

4)范德华力

磁流变液中的两个磁性颗粒接近时，一个磁性颗粒的脉动轨道电子诱导另一个磁性颗粒的振荡偶极子，产生范德华力。若颗粒间的距离为其直径的3～4倍时，范德华力的影响可以忽略不计。磁性颗粒容易相互吸引并发生团聚作用，这正是受范德华力影响。磁性颗粒i受到其他颗粒的总范德华力可表示为

(10)

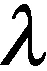
5)磁场产生的力矩

磁性颗粒被磁化后可以看作磁偶极子，外磁场作用使磁偶极子发生偏转。磁偶极子受到周围颗粒以及外部磁场的总力矩可表示为

(11)

6)粘性阻力产生的力矩

磁性颗粒转动时，因受到基载液粘性阻力的影响而承受力矩作用。磁性颗粒i受到的粘性阻力矩为

(12)

式中，ω为颗粒转动角速度，rj为垂直于旋转轴的单位向量且方向为轴心指向阻力作用点。

2.2 球形磁控机器人动力学分析

(13)

(14)

(15)

(16)

当颗粒磁化、结链后，通过单位截面内的链条数为n，可表示为

(17)

式中，V为磁流变液体积，φ为磁流变液体积百分率，s为横截面面积，L为颗粒链长度。磁场转动过程中，假设磁性颗粒链以完整的链状形态转动，颗粒间的距离会有所变化。如图5所示，单链对腔体壁面的载荷方程为

(18)

图5 磁性颗粒链变形示意图

图5中，q表示多粒子结合链对腔体壁面的载荷，rq表示双粒子结合链对腔体壁面的载荷。

通常颗粒本身不是规则的球体，颗粒链的方向并非都平行于磁场方向。但是，由于颗粒链众多，本研究假设颗粒链偏离磁场方向的规律服从正态分布，即

(19)

式中，Φ为磁性颗粒链与外部磁场方向的夹角，ζ为方差，为均值。颗粒链对腔体内壁施加的单位面积载荷为

(20)

考虑到颗粒链转动过程中会受到基载液的粘性阻力作用，磁流变液对腔体施加的单位面积总载荷为

(21)

根据球形磁控机器人矩形腔壁面受到的均匀载荷，机器人的驱动磁矩可表示为

T=(Ql2)/4=

(22)

假设夹角Φ与机器人矩形腔体和磁场方向的夹角θ近似相等，磁流变液的密度为4.5 g/mL，磁性颗粒半径rk取500 nm，磁场强度H为105A/m。结合式(1)和(22)，建立驱动力矩T与变量θ的对应关系T(θ)。将该机器人的CAD模型导入软件Maxwell(19.2)中，并利用参数化扫描逐步增大磁流变液自身磁化方向与外部磁场方向间的夹角θ，观察驱动力矩T的变化情况。

图6 磁矩随夹角θ的变化

利用外部旋转磁场驱动该球形机器人，响应速度快，且球形磁控机器人的滚动速度与外部磁场的旋转速度保持相对一致。因此，在一定磁场强度下，通过控制外部旋转磁场的频率和方向，可实现对该机器人运动速度和方向的可靠控制。

3 球形磁控机器人实验分析

3.1 球形磁控机器人速度检测系统

由于球形磁控机器人的运动参数无法利用传统接触式传感器测得，本研究通过图像处理对球形磁控机器人的运动参数进行获取，图像处理流程如图7所示。首先，利用工业相机(海康威视：MV-CA050- 11UM)连续采集球形磁控机器人运动图片，并将数据存入指定文件夹中。当文件夹中的图片数量超过2时，开始计算图片中球形磁控机器人的中心点坐标；利用相邻图片中机器人中心点坐标的变化来计算位移；根据采集两帧图片所消耗的时间，计算球形磁控机器人的运动速度。最后，随着机器人的运动，速度和位移数据也在不断更新。

图7 图像处理流程图

根据上述原理要在图片中检测到圆，首先假设圆半径r已确定，此时平面点(x,y)又已知，根据表达式(x-a)2+(y-b)2=r2，则(a,b)的轨迹变为以(x,y)为圆心，r为半径的圆；当r不确定时，(a,b,r)的轨迹变成了顶点为(x,y)的一个圆锥，参数(ai,bi,ri)、(aj,bj,rj)、(ak,bk,rk)表示的锥面的交点A为中心点，如图8所示。

通过霍夫变换圆检测算法可以获得球形磁控机器人在每帧图片中中心点的位置坐标，可用于计算机器人的运动速度和位移。另外，图像的尺寸和分辨率对霍夫变换圆检测算法的计算速度影响显著。因此，在读取图片后，需要对图片的尺寸和分辨率进行修改以提高运算速度，同时又要保留图片中的关键信息，高斯金字塔可以为这一问题提供有效帮助。高斯金字塔为图像信息的多尺度表征，利用高斯模糊对图片进行处理并进行向下取样，如图9所示。

图8 霍夫变换的圆检测原理图

图9 高斯金字塔

金字塔每一层按自下而上的顺序编号，伴随金字塔等级越高，图片尺寸越小。图像经过一次高斯金字塔的处理后，其尺寸缩减为原来的1/2。通过对原图像不断的迭代就会得到整个金字塔，OpenCV提供了pyrDown函数来实现图像的向下采样。利用高斯金字塔进行4次操作，效果如图10所示。

图10 高斯金字塔处理的图片

3.2 实验台基本构成

本节搭建了球形磁控机器人运动控制实验台，可实现机器人的运动控制和速度检测。如图11所示，实验台主要由工业相机、环形光源、三维亥姆霍兹线圈、上位机显示器、示波器、信号发生器以及OPA549功率放大器组成。信号发生器可产生不同频率的正弦信号，最高为15 MHz、最小分辨率为0.01 μHz。这种可调频率的正弦信号通过OPA549功率放大器进行放大，可连续输出8 A电流，最大峰值为10 A。当三维亥姆霍兹线圈接收到功率放大器的放大信号后，产生空间变化的磁场来实现机器人运动。该线圈内部具有40 mm×60 mm×80 mm的空间磁场，单轴线圈在8 A电流时能够产生10 mT的磁感应强度，具体结构参数如表1所示。此外，通过3D打印技术(打印机：Preform 2.0)，采用光敏树脂材料打印该磁控机器人的球形壳体。磁流变液通过注射器填充到矩形腔内，最后用胶水将注射孔密封，样机如图11所示。

图11 球形磁控机器人运动特性测试实验台

表1 三维亥姆霍兹线圈结构参数

如图11所示的三维亥姆霍兹线圈，假设在x-z平面中，当磁场方向在一个周期内偏转360°时，x轴与z轴方向上的磁感应强度B可表示为：

(23)

式中，B0为变化磁感应强度的幅值大小，mx与mz分别为x轴与z轴方向上的单位矢量。根据式(23)，若要实现平面内磁场偏转，需要在两个对应轴线方向上分别施加不同初始相位的正弦变化磁场。因此，在三维亥姆霍兹线圈中通入不同相位的正弦电流信号，可得到空间的旋转磁场，能够实现对该球形磁控机器人的运动控制。进一步地，调节正弦信号频率，改变磁场旋转速度，能够实现对该球形磁控机器人速度的调节。另外，若增大磁场幅值B0，球形磁控机器人可提高运动响应时间，但是稳定后的运动速度和运动方向不会改变，因此本研究B0取常数10 mT。

3.3 实验结果分析

首先，在工作平面内放置障碍物，测试球形磁控机器人的运动可控性和灵活性。通过控制外部旋转磁场的旋转方向，实现该机器人不同运动方向的调整。如图12所示，通过相机记录了球形磁控机器人不同时刻下的运动位置，可以看出该机器人能够越过障碍，具有较高的运动灵活性。

另外，球形磁控机器人的加速度特性也在实验中测试。设置外部磁场的旋转加速度分别为0.10、0.15、0.20、0.25和0.30 r/s2，该球形磁控机器人的平均速度变化规律如图13所示。实验结果表明：在恒定加速度下，球形磁控机器人的平均速度变化近似线性增加，与外部旋转磁场的变化规律基本吻合。

图12 球形磁控机器人运动截图

图13 不同加速度的球形磁控机器人平均速度变化情况

最后，根据第2节中对球形磁控机器人的动力学分析，通过调节空间磁场的变化频率来测试机器人的速度变化特性。本研究分别向三维亥姆霍兹线圈通入频率为0.4、0.6、0.8以及1.0 Hz的正弦信号，检测磁场在不同旋转频率下该球形磁控机器人的速度变化特性。如图14所示，在不同磁场环境下，该球形磁控机器人的运动速度存在不同程度的波动。

球形磁控机器人的直径为4 mm，在频率0.4、0.6、0.8以及1.0 Hz的旋转磁场下，理想运动速度分别为5.02、7.54、10.04和12.56 mm/s。根据图14所示的实验测试结果，在频率为0.4、0.6、0.8以及1.0 Hz的旋转磁场下，机器人运动的平均速度分别为4.77、6.62、9.48和11.40 mm/s。相较于平均运动速度，最大波动幅值分别为12.65%、12.86%、13.24%以及14.12%。

通过以上3种对球形磁控机器人运动特性的测试，结果表明：机器人运动可靠，能够绕过不同的障碍物；在匀加速变化磁场中，该机器人速度变化趋势与外部磁场变化趋势基本相同；在恒定频率的旋转磁场下，该球形磁控机器人运动速度在一定范围内波动，平均速度与理论值接近。另外，通过这些实验发现，当磁场方向变化较快时，该球形磁控机器人可能会出现运动迟滞现象；在设置匀速转动时，该机器人有一定的速度波动，且随磁场频率的增大而增大。产生这些运动误差的原因较多，一方面是由于外部磁场旋转时，磁流变液中磁性颗粒链伴随磁场方向的变化而改变，颗粒链中磁性颗粒的相对位置不断变化，颗粒链的结构处于破损和重组的动态变化中，施加于机器人壳体壁面的作用力不稳定而导致机器人整体运动迟滞或者速度波动。另一方面，是由于空间磁场分布不均匀，磁流变液的颗粒产生沉淀、物理性质下降等。

图14 不同旋转磁场下球形磁控机器人的运动速度情况

4 结论

(1)磁流变液作为一种智能材料，针对传统磁控机器人永磁体驱动材料的局限性，设计了一种基于磁流变液的球形磁控机器人。

(2)根据磁流变液的流变特性，分析了粒子链的力学模型，建立了该球形磁控机器人的动力学模型，并进行仿真分析。

(3)设计了该球形磁控机器人的速度测试系统，并开展了越障实验、加速度实验和恒速度实验。通过实验结果可以看出，该球形磁控机器人易于控制并且运动稳定、可靠。