空间圆钢管K型相贯节点刚度公式数值研究

卢栋炎，何星传，杨健生，彭林欣*

(1.广西大学 土木建筑工程学院， 广西 南宁 530004；2.工程防灾与结构安全教育部重点实验室， 广西 南宁 530004；3.广西防灾减灾与工程安全重点实验室， 广西 南宁 530004)

0 引言

钢管相贯节点因其有着良好的受力性能，维护性能，施工简便，外形美观等优越性，国内外越来越多大型管状结构采用相贯节点连接方式[1-2]。CHOO等[3- 4]考虑边界条件和主管应力对厚壁K型节点轴向承载力的影响，通过试验及有限元方法分析，得到节点承载力预测公式；李自林等[5-10]通过试验研究了圆钢管相贯节点的极限承载力、受力性能和破坏模式。支旭东等[11]通过试验与有限元分析，比较X型相贯节点有无内置加强板时对节点承载力的影响，结果表明内置加强板能显著提高节点极限承载力。《钢结构设计规范》(GB 50017—2017)[12]仅给出相贯节点支管承载力计算公式，并未对K型相贯节点的抗弯刚度进行规定。FESSLER等[13-14]根据多支杆环氧树脂管状相贯模型的试验结果回归了空间单支管节点和多支管节点的刚度参数方程。王伟等[15]采用正交试验法，通过ANSYS有限元模拟回归得到了圆钢管T、K型节点平面刚度参数公式。陈映等[16]通过有限元分析法考虑主管受轴力作用对K型弯管节点的轴向刚度进行参数化分析，得到节点轴向刚度的计算式。

以上针对圆钢管相贯节点的研究，主要包括节点的极限承载力、相贯节点刚度加强方式、破坏模式及面内刚度计算式。但由于试验加载条件限制，大多数以平面内的加载方式为主，对于空间结构，尤其是空间K型相贯节点平面外刚度计算式的研究较少。为此，文中选取“世界第一拱”主跨为575 m中承式钢管混凝土拱桥——平南三桥的K型相贯节点，在对拱肋泵送混凝土，且混凝土尚未凝固的施工阶段，进行节点弹性平面内、外刚度的数值分析和试验研究。为了较准确地描述大跨度、超大跨度钢管拱桥空间K型相贯节点的受力性能和平面内、外刚度变化规律，本文采用正交试验法确立计算模型的参数，通过ABAQUS软件建立K型节点的有限元模型并进行分析，应用多元线性归回理论拟合出空间K型相贯节点的平面内、外刚度计算式，选取平南三桥在拱肋泵送混凝土阶段受力最危险节点，进行平面内、外共同受力作用下该节点的单调弹性加载缩尺试验，拟合计算式结果与试验结果及有限元结果对比较为吻合，验证了有限元建模及拟合计算式的准确性，并为实际工程设计提供参考。

1 节点变形机理及刚度

1.1 节点变形机理

圆钢管相贯节点在支管受力作用下产生的变形由两部分组成，一部分是主管的整体位移及转角，另一部分是节点的局部位移及相对转角。如图1所示，当支管1受轴力作用时，相贯节点会产生竖向变形和平面内的转动变形；当支管1受到平面内弯矩作用时，节点会产生竖向变形和平面内的转动变形。为了描述节点的变形情况，如图1(a)所示，在相贯节点处定义参考点di(i=1,2,…,8)的位置，括号中表示背侧参考点的位置，以支管1为例，则有

Δ1=(d1+d2+d3+d4)/4,

(1)

Δ2=(d4-d2)sinθ1/(d-t),

(2)

Δ3=(d3-d1)/(d-t),

(3)

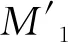
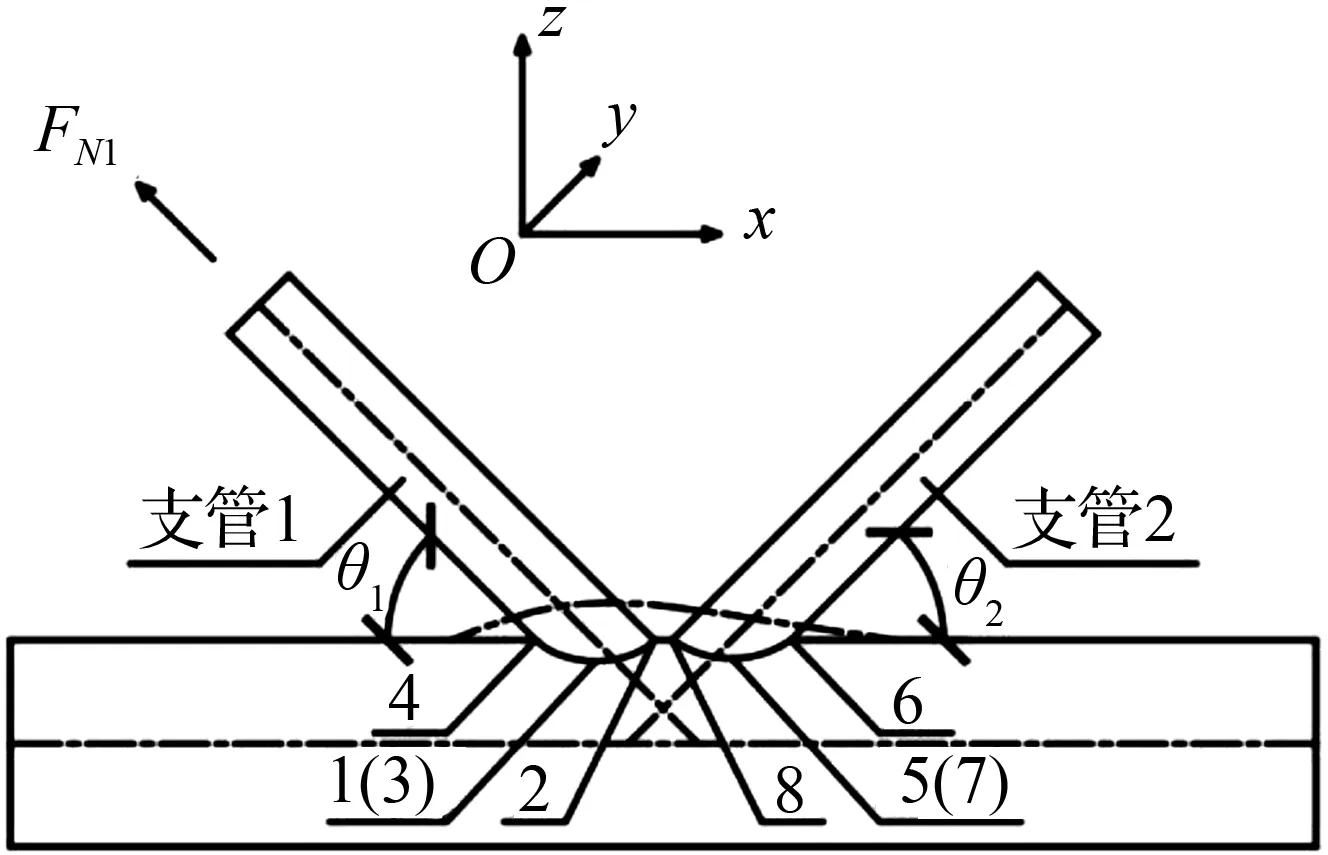
(a) 轴向拉力

1.2 节点刚度

基于1.1中相贯节点的变形机理，定义相贯节点的刚度为相贯节点发生单位变形时受到外荷载的大小，并取坐标系x轴为沿主管轴线向右为正，y轴定义为垂直纸面向里为正，z轴垂直主管轴线向上为正。

节点模型采用以下基本假定：

① 焊接对相贯节点的影响忽略不计;

② 模型始终处于弹性阶段，且处于小变形范围;

③ 主管轴向刚度远大于其径向刚度，可不考虑节点沿主管轴向的位移;

④ 节点的抗扭刚度远大于其抗弯刚度，可不考虑节点的扭转变形。

空间节点刚度计算式为:

Kij=Fi/Δj，

(4)

其中：Δj为相贯节点在节点j方向上的节点变形，Kij为相贯节点的刚度，表示该节点在j方向上发生单位位移，需在i方向上受到的荷载(i=1,2,3,4,5,6;j=1,2,3,4,5,6)。F1，F2，F3分别表示为结点1在坐标系z，y，x方向上的竖向力，平面内弯矩与平面外弯矩；F4，F5，F6表示结点2在坐标系z，y，x方向上的竖向力，平面内弯矩与平面外弯矩；Δ1，Δ2，Δ3表示结点1在坐标系z，y，x方向上位移，平面内转角与平面外转角；Δ4，Δ5，Δ6表示结点2在坐标系z，y，x方向上的位移，平面内转角与平面外转角。

在空间受力作用下，K型圆钢管相贯节点的荷载与位移的关系可以表示为

[F]6×1=[K]6×6[Δ]6×1,

(5)

其中：[K]6×6为相贯节点的刚度矩阵，Kij为该矩阵的元素。

一般而言，刚度矩阵难以通过有限元计算得到，而是通过柔度矩阵求逆得到，定义柔度矩阵

{Δ}6×1=[f]6×6{F}6×1,

(6)

其中：柔度矩阵[f]中的元素fij表示该节点在j方向上受到单位力，引起i方向上的位移。

以柔度矩阵中的元素f1j(j=1,2,3)为例，计算K型节点柔度的计算式可以根据以下公式得到

f11=Δ1/FN1sinθ1,

(7)

f12=Δ1/M1,

(8)

(9)

2 节点有限元分析

2.1 有限元相关参数

参照FESSLER等[14]的研究，如图1(a)所示，选取影响空间K型相贯节点刚度的主要参数为支管1与主管轴线夹角θ1(锐角)，支管2与主管轴向夹角θ2(锐角)，支管管径与主管管径之比β=d/D，主管管径与支管间距之比δ=D/a，主管管径与主管管壁的两倍之比γ=D/(2T)，支管管壁与主管管壁之比τ=t/T。

图2 有限元模型

如图2所示，有限元分析使用ABAQUS软件，采用S4R单元，每个模型网格划分均不少于15万个单元，材料Q345钢材，泊松比υ取0.3，弹性模量E取206 GPa，主管管长12 m，支管轴线长5 m，模拟空间K型相贯节点试验。主管两端固结，支管端部自由。

为得到K型节点拟合公式，需对6个参数，每个参数包含5种不同状态建立模型及计算并对结果拟合分析，对所有参数及其状态进行单参数分析，需建立56即15 625个模型。本文采用正交试验法确定最有代表性的25个模型及其参数取值，可以以更少的模型得到最优的结果。表1的L25(56)正交表列出了各个模型参数的取值，该取值范围涵盖了平南三桥所有的K型节点尺寸，并且符合规范的要求。

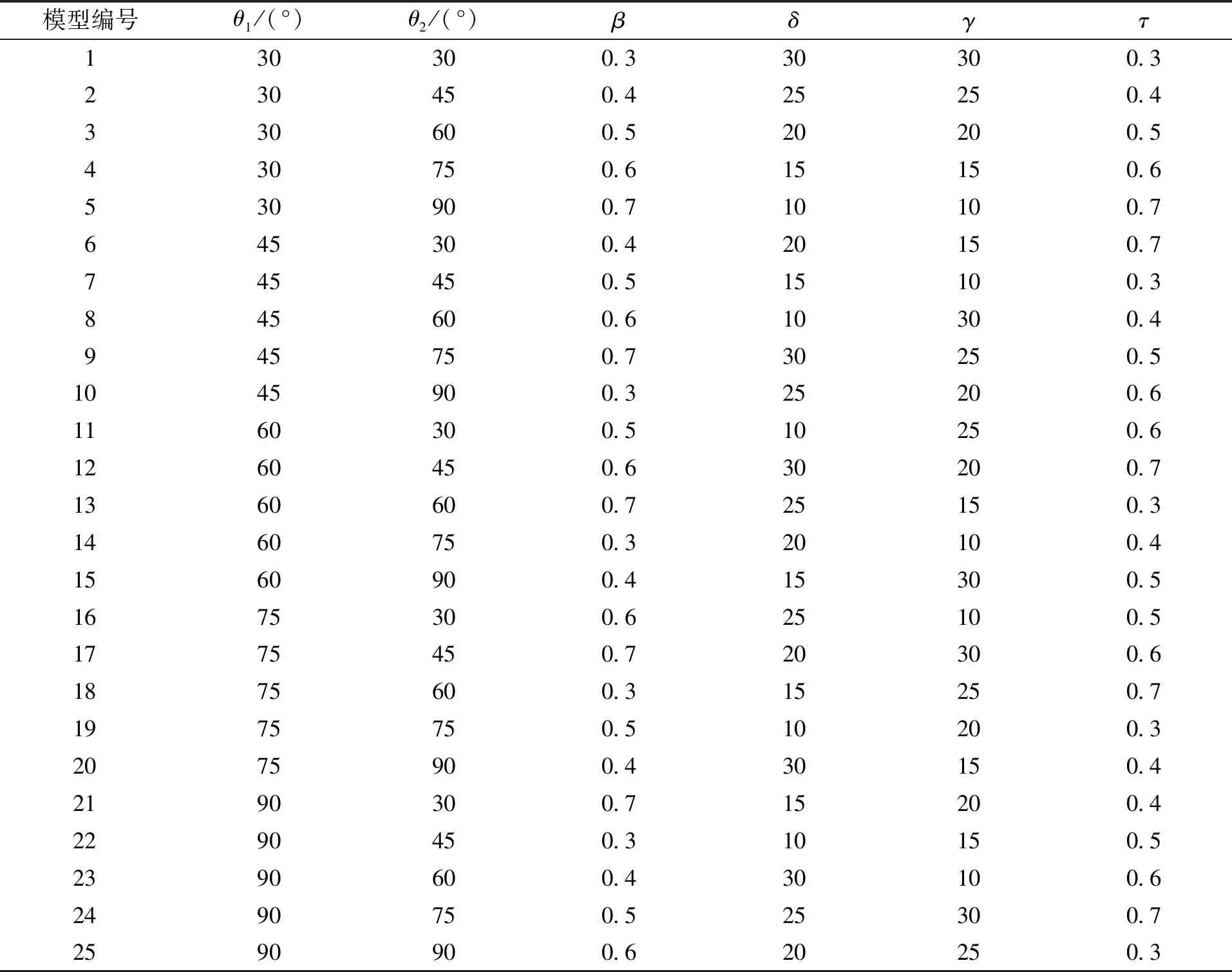
表1 K型节点正交表

2.2 节点柔度矩阵元素拟合式与有限元结果对比及分析

参照王伟等[15]的研究，θ1和θ2采用正弦函数变换可更好地拟合结果，对以上有限元模型的柔度矩阵元素计算结果使用SPSS统计软件进行多元线性回归分析，得到各相关参数的常量，采用调整后的R2作为回归公式的显著性检验。式(10)中，R2为回归平方和与总平方和的比值，该比值越大，表示拟合计算式越精确，回归效果越显著。

(10)

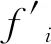
(11)

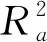
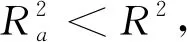
节点柔度矩阵元素拟合式结果与有限元结果对比图如图3所示。从图3中可以看出，各结点柔度矩阵元素拟合式结果与有限元结果吻合程度较高。其中，拟合式(12)～(17)的调整后R2均大于0.969，拟合式(18)的调整后R2大于0.974，拟合式(19)的调整后R2大于0.948，拟合式(20)调整后的R2大于0.945，拟合式(21)的调整后的R2大于0.902，拟合式(22)的调整后的R2大于0.984。说明各拟合式均能较好地描述节点各柔度矩阵元素的变化规律。

对比图3(a)、图3(b)、图3(c)可以看出，K型结点竖向刚度较强，平面内抗弯刚度较弱，平面外抗弯刚度较差。从图3(d)中可以看出，受力结点受轴力作用时引起受力结点平面内弯曲，可能原因是结点受轴力作用时，结点域左右两侧的刚度不同。结点域上有支管一侧，支管对该侧结点域的刚度有加强作用，结点域上无支管的一侧无刚度加强，结点受拉力作用时，受力结点向相邻结点方向弯曲。同理，结点受平面内弯曲作用时，结点不仅有平面内弯曲，也有竖向的位移。从图3(f)中可以看出，结点受轴力作用引起相邻结点的平面内弯曲和结点受平面内弯曲作用时引起相邻结点竖向位移，主要原因可能是结点受拉力作用时，相邻结点靠近受力结点的一侧变形较另一侧大，引起结点往受力结点的反方向弯曲；当结点受平面内弯曲作用时，相邻结点靠近受力结点的一侧变形较另一侧大，结点产生竖向位移。从拟合式(12)～(18)、(20)中可以看出，上述结点刚度与节点的构造形式有关，即f11和f44拟合式互为等价；f22和f55拟合式互为等价；f33和f66拟合式互为等价；f12、f21和f45、f54，f24、f42和f15、f51拟合式互为等价。

对比图3(a)和图3(e)可以发现，拉伸元素f11、f44与f14、f41的变化规律是相似的，表明结点受轴力作用时，亦会在相邻结点产生与之相似的变形。从图3(g)中可以看出，弯曲元素f25、f52为正的模型8、9、10、15、17、24、25中，参数γ取值都较大，主管的抗弯刚度较低，容易引起整体变形，而β与τ较大，支管的刚度较强。产生该现象的可能原因是支管对节点平面内抗弯刚度有较大影响，受力结点受正向平面内弯矩作用引起相邻结点的弯曲变形比引起整体弯曲变形小时，弯曲元素f25、f52可为正。从图3(h)中可以看出，结点的平面外抗弯刚度相对结点平面内抗弯刚度较弱，当支主管径比β，主管外径与支管间距之比δ，主管径厚比γ降低时，能提高节点的抗平面外刚度。

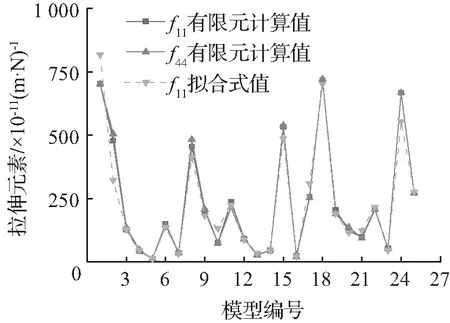
(a) 拉伸元素f11、 f44

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

f13=f16=f43=f46=f31=f34=f61=f64=0,

(23)

f23=f26=f53=f56=f32=f35=f62=f65=0,

(24)

其中：30°≤θ1≤90°；30°≤θ2≤90°；0.3≤β≤0.7；10≤δ≤30；10≤γ≤30；0.3≤τ≤0.7。

通过上述拟合式(12)～(24)及图3，从各因素的指数和常数可以看出，主管外径与主管壁厚之比γ对节点局部刚度起主要因素作用，主管外径与支管间距之比δ和支管外径与主管外径之比β对相贯节点局部刚度影响也较大，支管壁厚与主管壁厚之比τ对相贯节点的刚度影响相对较小，原因是主管壁厚增加，能够极大增加主管惯性矩，提高节点的刚度，而支管壁厚和支管外径与主管外径之比的增加能够提高节点平面内弯曲刚度，原因是节点平面内弯曲时，支管刚度提高能够有效提高主管节点的抗弯刚度，但支管壁厚对节点竖向刚度影响较小。

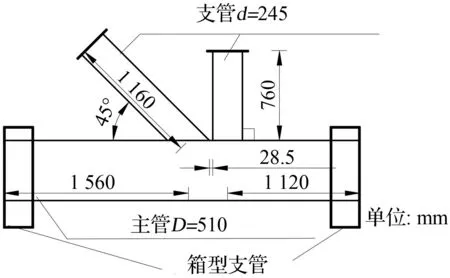
图4 试件尺寸

3 节点刚度试验研究

3.1 节点试验

本文依据平南三桥工程背景，节点采用圆钢管K型相贯节点，由于主管曲率较小，节点域内可近似按照直主管考虑。使用MIDAS有限元软件对平南三桥建立全拱模型，模拟拱肋灌注混凝土，但混凝土并未凝固形成有效承载力时，混凝土对拱肋及腹杆仅起重力荷载作用，经计算取应力最危险处的节点进行试验研究。

对平南三桥K型节点进行轴力、平面内弯矩、平面外弯矩共同作用下的单调弹性加载缩尺试验，缩尺比例为1∶2.8。如图4所示，圆钢管K型相贯节点试件的主管截面实测外径D=510 mm，壁厚t=14 mm，长度L=3 000 mm，2支管截面实测外径d=245 mm，壁厚t=6 mm，支管1长度1 160 mm，支管2长度760 mm。两支管与主管在相贯线处焊接而成，支管1轴线与主管轴线的夹角为45°角，交点距主管左端部1 560 mm；支管2轴线垂直于主管的轴线，其交点距主管右端部1 120 mm，两支管间距28.5 mm。主管两端嵌入箱型支座，相贯处采用焊接固定。主管、支管均采用Q345钢材，试验屈服强度为306 MPa。

3.2 加载方法及测试方案

如图5所示，试验前为方便测量相贯节点各参考点的竖向位移，将钢条的一端与对应点焊接在一起，另一端自由并垂直支管与主管所在的平面，通过使用千分表测量另一端的竖向位移间接获取节点上对应参考点的竖向位移，在主管与钢箱交界处布置千分表测量主管端部的竖向位移。

采用杆端加载方式，如图6所示，试验加载采用作动器1沿支管1轴线施加轴向压力，设定65 kN，采用位移控制；作动器2对支管2杆端上的偏心支座施加偏心拉力，设定50 kN，采用位移控制，施力点与支管2轴线平面内偏心227 mm，平面外偏心227 mm，作动器2与作动器1按1∶1.25同步按比例加载，当作动器2达到设定载荷以上时停止加载。边界条件设置如图6所示，主管两端采用钢箱固结，将钢箱放置于混凝土地面，使用反力梁压紧钢箱限制其上下位移，通过螺杆将反力墙与钢箱连接限制其左右位移。

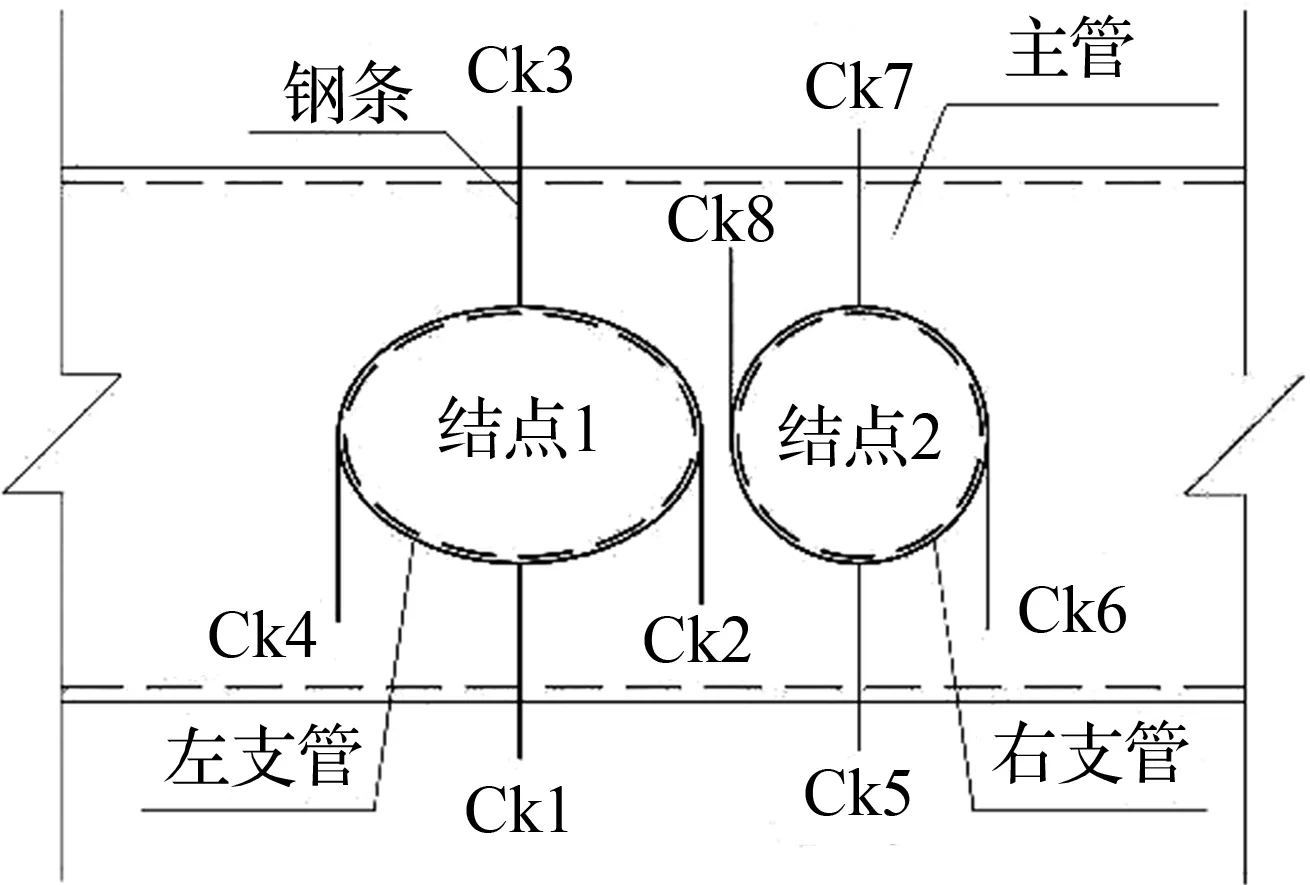
图5 测点布置

图6 试验装置

3.3 试验现象及参数公式的检验

通过对试件加载全过程观察，发现试件在外观上基本没有任何变化，偏心支座与支管端部连接处没有发出明显声音，主管两端端部千分表读数始终为零，节点区域千分表读数较为明显。

图7 有限元模型

根据节点的试验研究，如图7所示，建立与试件尺寸、几何构造、材料、边界条件以及加载方式完全相同的有限元模型，得到有限元计算结果，试验结果与有限元结果误差均小于11.1 %，说明有限元建模的合理性。为检验本文拟合的节点局部刚度参数公式的正确性，将参数公式计算值与试验值和有限元计算值进行比较。图8为公式值与试验结果对比图，图8(a)、(d)为结点1和结点2的荷载与竖向位移关系曲线。可以看出两荷载位移曲线趋势都非常接近，但结点2的竖向位移较结点1高，说明结点的竖向位移受其竖向分量的轴力影响大。拟合公式的结果与试验结果基本一致，曲线吻合较好，与有限元结果误差均小于9.0 %。图8(b)、(c)、(e)、(f)为结点1和结点2的荷载与弯曲转角的关系曲线。可以看出弯曲转角与荷载之间呈较为线性的关系。对比结点1或结点2的参数公式结果和试验结果可以发现，结点的平面内弯曲变形较平面外弯曲变形小，说明结点的平面外刚度较平面内刚度差。而从结点1与结点2的面内和面外的参数公式结果和试验结果看，结点2的变形比结点1大。拟合公式的结果与试验结果基本一致，曲线吻合较好。

产生以上误差的原因可能有以下2点：

① 拟合式是根据K型节点的主要参数(θ1,θ2,β,γ,δ,τ)，结合正交试验法，并运用多元线性回归分析拟合而得，并非节点的精确解，存在一定的误差。

② 试件是由多根钢管焊接而成，钢管各部分材料属性可能不尽相同，与通过有限元模型拟合得到的拟合式之间存在一定误差。

(a) 结点1竖向位移

4 结 论

为研究圆钢管K型相贯节点平面内、外刚度性能，本文以平南三桥为工程背景，基于正交试验法设计计算模型的参数，通过数值分析、模型试验、理论分析拟合出空间圆钢管K型相贯节点的参数公式，并得到以下结论：

① 在材料属性一定的情况下，空间圆钢管K型相贯节点的刚度与支管和主管的几何尺寸，构造形式有关。其中主管外径与壁厚之比γ对相贯节点的刚度起主要因素作用，主管外径与支管间距之比δ和支管外径与主管外径之比β对相贯节点局部刚度影响较大。

② 对K型节点进行轴力、平面内、外弯矩共同作用下得到的试验结果与K型节点刚度参数公式结果吻合较好，该参数公式与有限元结果最大误差为11.1 %，可应用于工程实际。