圆锥曲线题目的解答与延伸

曹珍玉

【摘 要】圆锥曲线这一部分的知识非常重要。虽然其属于平面解析几何，不如立体几何抽象，但是圆锥曲线题较大的计算量和较高的计算难度导致学生解答时常出现各种问题。梳理圆锥曲线题的基本解题思路，无论是对学生解题还是教师教学都有着非常重要的意义和作用。

【关键词】圆锥曲线;解答;延伸

圆锥曲线这一部分的知识非常重要，尤其是在高考试卷上经常以压轴题的方式出现，给学生带来了一定的困难。其实相较于其他部分，此部分的知识理解难度并不大，但整体的计算量却比较庞大。解读这一部分的题目，梳理整个计算流程，有助于教师更好地认识这一部分的教学。

1   圆锥曲线题目解析

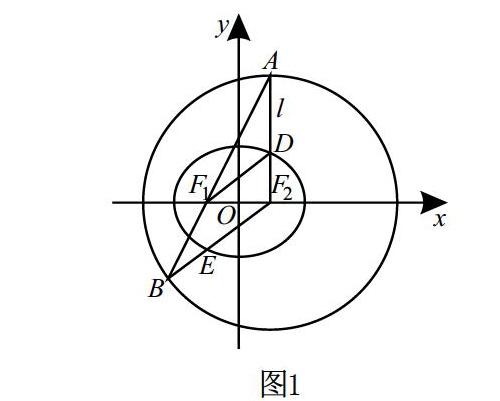
1.1  问题的提出

结合这几道题可以得出，圆锥曲线这一部分的知识非常重要，而且出题形式的变动空间相对有限。考试中主要考查椭圆、双曲线和抛物线本身的性质以及直线和这三种曲线的位置关系。直线和曲线相交的情况下，联立方程组是一個非常重要的解题点，据此可延伸出相关的斜率问题、向量问题以及角度证明问题。此部分的题目虽然不像三角函数与向量、立体几何与平面解析几何那般有着非常密切的联系，但是在出题形式上适当结合其他板块的知识也是一种创新性的表现。虽然出题形式上有所创新，但并没有抛弃教材知识的基础，圆锥曲线部分的基础知识仍然在解答题目的过程中扮演着至关重要的角色。所以，题目形式虽有所变化，但是考查的知识点却还是基础内容。基于此，学生需要具备灵活的解题思维，对知识的理解不能仅停留在表面，而要迈向更深的层次。

【参考文献】

[1]党彦平.高中生圆锥曲线学习障碍与应对策略[J].华夏教师，2019（35）.

[2]陈子航.回归定义，巧解圆锥曲线问题[J].语数外学习（高中版中旬），2019（2）.