关于交换环上保持伴随矩阵的函数

戴娇凤，谭宜家

(福州大学 数学与计算机科学学院，福建 福州 350108)

保持问题是矩阵代数中的重要研究内容之一，它在系统控制、微分方程等领域有着广泛的应用。最早的保持问题出现在1897年，G.Frobnius研究了域上矩阵空间保持行列式的线性算子，获得了n×n复矩阵空间上保持行列式的线性映射f的形式[1]。自那以后，多位学者对保持问题的相关内容进行了研究，取得了丰富的研究成果[2-10]。2011年，H.Yao等引入了保持某种矩阵性质的函数[11]，开辟了研究保持问题的一个新的方向。2017年，樊玉环和马艳芬刻画了域上四阶上三角矩阵空间保持伴随矩阵的函数形式[12],并指出任意阶上三角矩阵空间保持伴随矩阵的函数有待进一步探讨。本文在上述基础上进一步探讨交换环上全矩阵空间和上三角矩阵空间保持伴随矩阵的函数，所得结果拓广了文献[12]的结论。由于一般交换环的非零元不一定可逆，本文的证明方法与文献[12]有所不同。

1 基本概念与符号

本文中，如无特别说明，R表示一个含有单位元1的交换环。

设f是R到自身的一个映射，Mn(R)和Tn(R)分别表示R上n阶矩阵空间和n阶上三角矩阵空间。对于任意A=(aij)∈Mn(R)， 定义f(A)=(f(aij))。

定义1设f是R到自身的一个映射，如果∀a、b∈R，均有f(a+b)=f(a)+f(b)，f(ab)=f(a)f(b)， 则称f是环R的一个自同态。

定义2[13]设A=(aij)∈Mn(R)， 定义A的行列式如下

detA=∑σ∈Sn(-1)π(σ)a1σ(1)a2σ(2)…anσ(n)

这里Sn是集合{1,2,…，n}的对称群，π(σ)是置换σ的逆序数。

设A=(aij)∈Mn(R)， 将A中元素aij所在的行和列划掉，剩下的元素 (排列位置不变) 构成的n-1阶矩阵的行列式称为元素aij的余子式，记作Mij。 再设Aij=(-1)i+jMij， 称Aij为元素aij的代数余子式。

定义3[13]设A=(aij)∈Mn(R)， 记

称A*为矩阵A的伴随矩阵。

定义4设f是R到自身的一个映射，如果∀A∈Mn(R)(或∀A∈Tn(R))，均有f(A*)=(f(A))*， 则称f是R上n阶矩阵空间(或n阶上三角矩阵空间)保持伴随矩阵的函数，这里A*表示A的伴随矩阵。

2 主要结论

定理1设f∶R→R是一个映射，n(n≥3)是一个正整数，则下列条件等价：

(1)f是R上n阶矩阵空间Mn(R)的保持伴随矩阵的函数；

(2)f是R上n阶上三角矩阵空间Tn(R)的保持伴随矩阵的函数；

(3)f=f(1)δ， 其中fn-1(1)=f(1)且δ是R的非零自同态。

为了证明定理1，先引入一个引理。

引理1设R是一个交换环，δ是R的一个自同态，那么对于任意A∈Mn(R)， 均有δ(detA)=det(δ(A))。

证明因为δ是R的一个自同态，所以，对于任意a∈R， 均有δ(-a)=-δ(a)。

设A=(aij)∈Mn(R)， 则

=∑σ∈Sn(-1)π(σ)δ(a1σ(1))δ(a2σ(2))…δ(anσ(n))(根据δ的定义及δ(-a)=-δ(a))

=det(δ(A))。

证毕。

定理1的证明(1)⟹(2)显然。

(2)⟹(3)：首先证明f(0)=0及fn-1(1)=f(1)。

设A=0⨁En-1∈Tn(R)， 由伴随矩阵的定义，计算可得

另一方面，由f的定义知

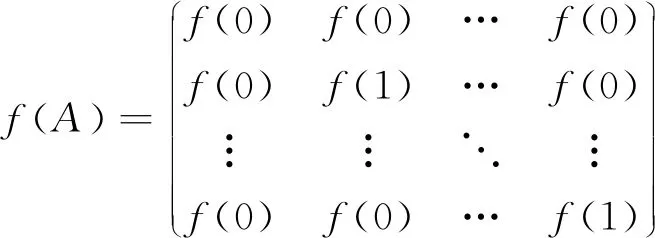
经计算，矩阵(f(A))*的(1，1)处元素是(f(1)+(n-2)f(0))(f(1)-f(0))n-2, (2，n)处元素是0。因为f保持伴随矩阵，所以f(A*)=(f(A))*。比较这2个矩阵的(2，n)处元素,得

f(0)=0

(1)

再比较这2个矩阵的(1，1)处元素，并利用(1)式，得

fn-1(1)=f(1)

(2)

进一步，对于任意的x,y,z∈R，设

另一方面，利用(1)式，有

于是利用伴随矩阵的定义和(2)式，得

f(-x)=-fn-2(1)f(x)

(3)

再比较这2个矩阵的(1，3)处元素，得

f(xz-y)=f(1)n-3(f(x)f(z)-f(1)f(y))

(4)

在(4)式中令y=0,并利用(1)式，得

f(1)n-3f(xz)=f(1)n-3f(x)f(1)n-3f(z)

(5)

在(4)式中令y=0,z=1，得

f(x)=f(1)n-2f(x)

(6)

由(3)式和(6)式，得

f(-x)=-f(x)

(7)

在(4)式中令z=-1,得

f(-x-y)=f(1)n-3(f(x)f(-1)-f(1)f(y))

(8)

利用(2)式和(7)式，整理(8)式，得

fn-3(1)f(x+y)=fn-3(1)f(x)+fn-3(1)f(y)

(9)

如果f(1)≠0， 令δ=f(1)n-3f， 则由(6)式知f(x)=f(1)(f(1)n-3f(x))=f(1)δ(x),即f=f(1)δ， 因此δ(1)≠0。进一步，由(5)式和(9)式，得

δ(xz)=δ(x)δ(z),δ(x+y)=δ(x)+δ(y)

所以，δ是R环的一个非零自同态。

如果f(1)=0， 则对于任意x∈R， 均有f(x)=f(1)n-2f(x)=0， 此时任取R的一个非零自同态δ， 均有f=f(1)δ。

(3)⟹(1)：对于任意i,j∈{1,2,…,n}，用A(i,j)表示矩阵A中去掉第i行和第j列后剩下的元素构成的n-1阶矩阵,则伴随矩阵A*中(i,j)处的元素为(-1)i+jdet(A(j,i))，所以，f(A*)中(i,j)处的元素为

f((-1)i+jdet(A(j,i)))=f(1)δ((-1)i+jdet(A(j,i)))

=f(1)(-1)i+jδ(det(A(j,i)))=f(1)(-1)i+jdet(δ(A(j,i)))(根据引理1)。

另一方面，因为f(A)=(f(aij))=(f(1)δ(aij))， 所以矩阵f(A)*中(i,j)处的元素为

(-1)i+jdet(f(1)δ(A(j,i)))=(-1)i+jf(1)n-1det(δ(A(j,i)))

=f(1)(-1)i+jdet(δ(A(j,i)))(根据(2)式)。

即对于任意i,j∈{1,2,…,n}， 矩阵f(A*)和矩阵(f(A))*中的(i,j)处的元素相同， 于是f(A*)=(f(A))*。

证毕。

由于任何域是交换环，并且域上任何非零自同态均为单自同态，所以在定理1中取n=4时，可由定理1的(2)和(3)得

推论设F是任意域，f是F到自身的一个映射，T4(F)表示F上所有四阶上三角矩阵全体，则f是T4(F)保持伴随矩阵的函数的充要条件是f=f(1)δ， 其中f3(1)=f(1)，δ是域F的单自同态。