一种基于小波变换的边缘检测算法

孙 青 锋

(1.安徽机电职业技术学院 电气工程学院，安徽 芜湖 241002；2.天津职业技术师范大学 自动化与电气工程学院，天津 300222)

0 引 言

图像是一个复杂的信息集合体，要快速准确地识别物体，关键是把握图像的典型特征。图像的边缘就是一个能概括图像的存在。图像的本质是像素点，而在边缘部分，有些点灰度变化明显。将这样一系列突出的点连接起来，能够表征物体的轮廓特征。此时，对于物体的认知，就转化为对于物体边缘的概括。边缘检测，就是基于引起图像灰度变化的物理过程，来描述图像灰度的变化[1]。图像的边缘检测，能实现以较少的关键特征信息提取来概括目标物体的目的，从而将图像间的运算由这些边缘特征来替代，提高运算效率。

1 经典边缘检测算法

边缘是描述图像局部特征的基础。像素邻域灰度变化的阶跃性，是标定边缘的基础。图像是一种二维信号，其定义边缘特征的方式，与一维连续信号不同。对一维信号，我们可以一阶导数最大或者二阶导数为零来定义边缘；而对于二维图像，常用图像灰度分布的梯度信息来表征边缘。通常，边缘检测包含滤波、增强、检测、定位四个主要步骤[2]。基于对原始图像的平滑处理和对变化的凸显，定位边缘点，进而明确图像边缘。

边缘检测理论自应用于图像处理以来，各国学者提出了很多算法。诸多算法里，微分法(如Roberts算子、Sobel算子和Laplacian算子等[3])和最优算子法(如LOG算子和Canny算子[4])较有代表性。

描述、表征图像的边缘特征，常用到幅度和方向这2个参数。对连续函数I(x,y)，在点(x,y)处，其梯度为一个矢量，定义为

(1)

梯度的幅值和方向分别为

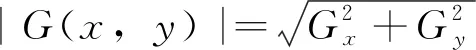
(2)

(3)

上述各类边缘检测算子，都经过实践的检验。其性能的判定，取决于应用场景的考量。总体而言，各具特色。一阶微分算子中，Roberts算子较容易实现，定位精度高，但抗噪性能较差。Sobel算子增强了对噪声的抗性，但增加了计算量和误定位率。二阶微分算子中，Laplacian算子能有效去除伪边缘，定位较准确，但受噪声的影响增大[5]。LOG算子是Laplacian算子的改良，通过函数滤波，抗噪性能改善。同理，Canny算子引入高斯滤波，增强了抗噪性，但边缘丢失率增加[6]。可以看出，传统边缘检测算法因图像多样性和自身局限性，在不同应用中都多少存在一定的问题，不断改进已有算法，融入新的特征，或者引入新的理念，提出新的算法，一直是众多研究者努力的两大方向。当前，随着模糊数学、神经网络、多尺度理论等的深入应用，不断推动着边缘检测算法的发展。

2 小波变换及其边缘检测算法研究

小波变换作为多尺度理论的代表，因其数学描述的完备性，广泛应用于图像处理领域。其中，在图像边缘检测方面，其具备的多尺度性能够很好地与传统算子结合，取得了较好效果，具有较大研究价值。

2.1 小波变换

在时域和频域都具有较好性能的小波变换，能够通过尺度函数和平移运算，将图像的高频成分和低频成分分离出来，后续再通过图像重构重新建构图像。这为图像处理的速度和多样化提供了重要基础。在各不同尺度对图像进行小波分解，将形成由高低频信息构造的金字塔结构。通过将低频细节与高频信息分别存放，方便对目标信息进行处理与利用。

在小波多分辨率理论发展历史中，MALLAT的快速小波分解算法[7]举足轻重，直接推动了小波变换理论应用进程。如图1所示，图1(a)简单表征了小波变换的二层分解情况。图像的二层分解，每层都通过不同的4个位置存放相应的图像信息。分别为低频信息、高频信息、水平和垂直分量(第一层以LL1、HH1、LH1和HL1来表示)。其中，下一层的分解，基于上一层的低频信息(例如，若是第二层分解，则基于第一层的LL1，依次类推)。图1(b)为实际分解效果。

图1 图像的小波分解

2.2 基于小波变换的边缘检测算法研究

边缘是图像中灰度发生不连续变化的地方。边缘与噪声均为高频信号。因此，在噪声环境中准确检测边缘特征比较困难。基于传统微分运算的边缘检测方法，难以准确区分高频的边缘和噪声。然而，抗噪性是图像处理及相关环节的重要性能保障，对噪声的适应性直接影响算法最终效果。正是基于这样的现实考量，利用小波变换对图像细节与高频的分解，具有重要意义。小波变换的时频特性，有利于边缘检测。

自从小波变换应用于边缘检测以来，大致有改良和改造两种思路。一是结合小波变换改良已有边缘检测算子，另一种是改造、提炼新的边缘检测算子。通过融入新性能或构建新的小波结构改善边缘检测。文献[6]、[8]属于改良型。文献[6]首先通过双边滤波代替传统高斯滤波改进Canny算子，然后通过小波变换增强图像高频细节而实现边缘检测。文献[8]中，用Canny算子和小波法分别提取边缘，然后融合优化，确定最终边缘。文献[9]、[10]中，通过结合插值小波采样理论和构建全向小波的方法，改进了传统MALLAT方法，提炼出新的边缘检测算法。

2.3 本文算法

利用小波变换的多尺度特性及其在图像分解后得到近似部分和概括部分的特点，将其应用于图像的边缘检测，在不同尺度上应用小波变换，对大尺度分解下的高频信息做抑制噪声处理，依据梯度方向模极大值和阈值筛选，获得各尺度上的边缘，充分把握细节和概貌，进而获得边缘图像。步骤如下：

1)对图像应用小波变换分解，将在不同尺度上获得四类系数，分别用Ai、HLi、HVi、HDi表示。其中，i表示尺度因子，A为近似系数，HL、HV、HD为水平、垂直、对角线方向高频系数。

2)对各尺度下的水平、垂直方向高频系数(HLi、HLi)进行运算处理。构建模值图像MZ(:,:,i)和幅角图像FJ(:,:,i)。

(4)

(5)

3)求模值图像和幅角图像的局部最大值，选定阈值，得到边缘点。

4)连接边缘点，获得不同尺度下边缘特征。重构确定最终图像边缘。

3 实验结果

本文实验结果在MATLAB R2018b环境下仿真得出。首先选用屋顶图像并分别叠加了椒盐噪声与高斯白噪声的图像作为实验图像，分别用Roberts算子、Sobel算子、Canny算子、LOG算子与本文提出的算法进行实验，并对比分析检测结果；然后将算法应用于其他图像，实验其适应性。图2为实验图像以及各方法比较结果。图2(a)左、中、右三幅图分别为待测原图、添加椒盐噪声(δ=0.01)图、添加高斯噪声(δ=0.01)图。后面各图分别为对应方法在对应情况下的结果。图2(b)为Roberts算子检测结果，其对噪声较敏感，且有些边缘缺失。图2(c)中Sobel算子在边缘位置和方向的检测有一些改进，有更好的抗噪性。但其边缘缺失较多，定位精度不够。图2(d)中，Canny算子受噪声干扰明显。图2(e)中，LOG算子能够平滑掉一部分噪声，但边缘仍有缺失。图2(f)为本文提出的基于小波变换的边缘检测算法，充分利用小波的多尺度特性，在抗噪性与精确定位方面取得了比较好的效果。

图2 屋顶测试图像及其边缘检测结果

图3 其他测试图像及其边缘检测结果

图3为本文小波检测算法适应性实验结果。在图3(a)和图3(e)两张测试图上，分别添加高斯噪声(δ=0.02),如图3(b)和图3(f)所示。对两张测试原图和添加噪声后的图用本文方法检测图像边缘，对应结果如图(c)、(d)、(g)、(h)所示，可以看出，本文提出的小波变换边缘检测算法，具有较好适应性。在两幅不同的图像上，均能较清晰、准确地检测出图像边缘。另外，在添加噪声后，具有较好的抗噪性。

4 结 论

利用小波图像分解对细节和概貌信息的分别存放，提取边缘特征，有效解决了边缘定位与噪声之间的矛盾。后续可在尺度空间理论、自适应阈值等方面作进一步研究，并结合实际应用，将图像边缘检测用于生产实践中。