G-SVD:一种基于高斯卷积和SVD的暗通道去雾算法

王诗毅，姚信威，姚 远

(浙江工业大学 计算机科学与技术学院，杭州 310023)

1 引 言

近年来，我国出现雾霾天气的几率大大增加，在雾霾条件下采集图像，原本较低的像素值被增大，而原本较高的像素值被降低，造成图像对比度的退化，给自动驾驶、目标检测等领域带来了极大的困难.因此，图像去雾技术具有重要的应用价值，已经成为图像视频处理[1]、计算机视觉和计算机图形学等领域的热点问题.

基于先验的暗通道去雾算法[2]是当前主流去雾算法模型之一，有大量学者对该算法进行了改进.面对暗通道去雾效果在特殊情况下能见度低的缺陷，Pal等人[3]使用三边滤波器(Trilateral filter)增强图像能见度，再使用S型(Sigmoid)传递函数增强图像对比度.Halmaoui[4]和Li[5]使用直方图均衡化增强图像可视化效果，其中前者使用模拟退火算法优化参数，而后者利用雾霾的呈现淡黄色原理，采用自适应直方图信道均衡自动调整参数.上述直方图方法仅仅关注图像亮度及对比度，不能得到图像的深度信息，因此往往会导致图像颜色发生畸变.He[6]等人使用收缩邻域的保边约束，使输出图像保持最大的平滑度，再通过HSI颜色通道上对图像进行处理，从而提高图像的有效性和可靠性.而对于暗通道的场景通透率和全局环境光的预估，Huang等人[7]利用导频滤波器获得非天空模糊图形的大气通透率，再利用天空、白云或者别的明亮区域的各类图像分类分析，预估天空各个部分的大气通透率，然而这类融合滤波方法难以保留图像细节.Zeng等人[8]提出了一种有效的正则化方法，通过增加场景辐射约束来求场景通透率.Cheng等人[9]则通过暗通道去雾模型，提出了一种处理时变消光系数性质的变分框架，并通过对观测到的亮度曲线分段函数拟合来估计全局环境光.Zhu[10]则提出了一种融合亮度和暗通道先验(Fusion of Luminance and Dark Channel Prior,F-LDCP)的算法，该算法将基于亮度模型和暗通道先验模型的传输值融合在一起，从而得到场景通透率.Chen等人[11]在暗通道的基础上引入局部暗通道，并对其进行映射处理，得到大气光强度粗值，再用导向滤波优化粗值，最后使用全变差正则化方法对初始图像优化，增强图像清晰度.秦等人[12]首先使用原暗通道模型预估全局环境光，在计算场景通透率过程中引入自适应优化计算以实现去雾.谭等人[13]在预估场景通透率后联合中值滤波和双边滤波对其细化，以满足天空区域的去雾处理.黄等人[14]使用深度学习方法去雾，利用自编码网络得到雾特征序列，再使用深度神经网络通过序列获得场景通透率，最后使用大气散射模型恢复无雾图像，然而使用深度学习方法往往需要大算力处理器和GPU，且往往耗费时间较长.

暗通道去雾算法所有推导都建立在全局环境大气光A已知的基础上，通常采用亮度大小前0.1%的像素点作为全局环境光，然而这仅仅对环境较亮的情况下结果有效，而在雾浓且雾不均匀的情况下，去雾效果往往不尽人意.其次，由于暗通道去雾算法存在景深变化，会在该变化边缘处产生一条较为明显的过渡带，出现块状效应[6].为解决块状效应和浓雾效果差这两个问题，本文提出了一种基于高斯卷积和SVD的暗通道去雾算法，即G-SVD，提升图像质量和能见度.实验结果表明，该算法可以较好的抑制块状效应，保留图像的边缘细节.通过与其他主流算法相比，本文算法在各个性能指标上的平均值均高于其他算法，说明该算法具有稳定性强，不易失真和不易产生颜色畸变的优点.

2 暗通道去雾算法

He[2]等人对大量户外有雾和无雾环境分析，提出了暗通道去雾算法.通用模型为科希米德公式(Koschmieder′s Law)[15]：

L(u,v)=L0(u,v)e-kd(u,v)+Ls(1-e-kd(u,v))

(1)

其中，L(u,v)为肉眼或者相机观测到的对象亮度，L0(u,v)为对象的原本固有亮度，(u,v)为各个像素点的坐标，Ls为大气光强，e-kd(u,v)为原本固有亮度的随着距离d(u,v)的增加而产生的指数衰减[2].在计算机图像和图形学中，公式(1)简化为：

I(x,y)=J(x,y)t(x,y)+A(1-t(x,y))

(2)

其中，I(x,y)为肉眼和相机看到的图像，J(x,y)为无雾图像，t(x,y)为场景通透率，A为全局环境大气光.

根据暗通道去雾算法原理，在彩色图像的RGB 3个通道中，大量统计表明，存在一些像素点值特别低，即该像素点的光强度较低：

(3)

公式(3)中C为RGB 3个通道，(x,y)为像素点坐标，因此暗通道即为在3个通道中像素点的最小值.

将公式(2)变形为：

(4)

对公式(4)两边同时取最小值：

(5)

根据暗通道理论，将公式(3)带入公式(5)，得到：

(6)

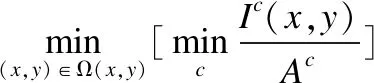
(7)

最终得到复原原图的公式为：

(8)

由于t(x,y)过小，则会造成图像失真，因此引入t0保证图像的可显示性.在公式(8)中，I(x,y)是已知的，要获得J(x,y)，则必须估计场景通透率t(x,y)和全局环境大气光A.

3 G-SVD去雾模型

3.1 估计环境大气光A

由于采用单一值作为全局环境光A，未考虑到局部环境下的环境大气光仍可能不同，因此本文采用了滑动窗口的模式预估每个像素点的环境大气光，滑动窗口大小3×3，每次滑动距离为1，如图1所示.

定义该滑动窗口中心点的环境大气光A为：

A=A0+Am

=min(AR,AG,AB)+Am

=min(IR⊗GK,IG⊗GK,IB⊗GK)+Am

(9)

公式(9)中，A0为通过高斯卷积方法预估的环境光，Am为偏差系数，IR，IG，IB分别为3×3的RGB图像块，⊗表示为卷积操作，GK表示为高斯卷积核(Gaussian convolution kernel).具体操作如图2所示，将3×3的滑动窗口分解为R、G、B 3个通道，并分别与高斯卷积核卷积相乘再求和，根据3×3滑动窗口的位置坐标，带入高斯距离公式：

(10)

最后进行归一化处理，使得9个坐标值和为1，得到最终的高斯卷积核.由于使用该方法预估环境大气光A偏小，会导致图像整体亮度偏低，因此引入偏差系数Am(公式(9))，通过大量实验验证，Am范围在0.2-0.28区间效果最好.

图2 高斯卷积预估环境光示意图Fig.2 Schematic diagram of Gaussian convolution estimation of ambient light

3.2 奇异值分解重构图像

基于暗通道模型去雾后会整体颜色较暗，且存在大量冗余信息和噪声，降低了图像含有的信息量，因此使用奇异值分解(Singular Value Decomposition)以用于图像去噪和图像重构.

假设矩阵A维度为m*n(m>n)，根据SVD原理得到：

(11)

其中U和V分别是AAT和ATA的特征矩阵，而

(12)

σ1≥σ2≥σ3≥σ4≥…>0

(13)

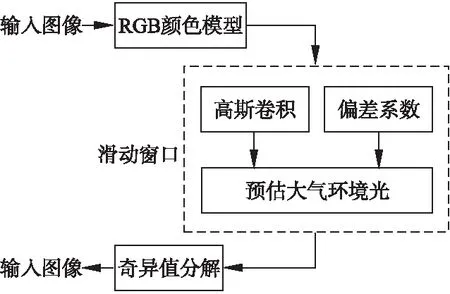
图3 G-SVD算法流程图Fig.3 G-SVD algorithm flowchart

根据公式(11)，我们可以使用前k个奇异值重构图像，减少图像噪声，提高清晰度.若k取值较大，则会导致图像去噪效果较差，保留过多冗余信息，而k取值较小，则会丢失原本的图像细节和原有信息，大量试验后，本实验中k均取值为图像宽的60%，此时图像有效信息保留最完善.整个G-SVD去雾算法流程如图3所示.

4 实验结果

4.1 实验环境

为验证本文所提方法的可靠性和有效性，本文实验在Intel(R)Core(TM)i5-4288u CPU，主频为2.6GHz，运行内存为8GB的PC机上运行，实验使用Matlab 2015a用于仿真.

4.2 主观视觉评价

为验证该算法的普适性，选取多种环境下的有雾图像(森林、小河、城市、天空和鹿)进行实验，此外，有雾图像的雾强度等级分别为：清雾、雾、大雾、浓雾和强浓雾，以丰富实验对象.目前去雾主流算法为基于去雾物理模型和基于图像增强算法两种.其中He算法[2]为基于去雾物理模型的去雾算法代表，通过提出暗通道去雾模型提升图像可见度；而Wang算法[16]为基于图像增强算法的去雾代表，其采用多尺度Retinex图像增强以去雾.为验证本文算法性能，将G-SVD与He算法[2]、Wang算法[16]对比，结果如图4所示.其中图4(a)为原图，图4(b)为采用本文算法G-SVD的去雾效果图，图4(c)为He算法[2]效果图，图4(d)为Wang算法[16]的去雾效果图.如图4所示，利用He[2]去雾算法处理后，整体色彩清晰度不足，局部区域甚至出现了块状效应(见图5)，通过局部放大图可以发现，第1行森林图像块状效应明显，导致视觉效果欠佳，并且在第2行小河图中，也出现了明显块状效应，颜色偏暗，细节保留不明显.而本文算法G-SVD在同一位置并未出现块状效应，且有效地改善了景深发生突变地方的色彩失真.此外，Wang算法[16]在第2行和第3行在天空区域出现了明显失真，并出现了色带，使得能见度不足.在第5行鹿图像中，本文方法对于图像中央远处树木的保留效果较好，而He算法[2]远处细节则完全消失.总体来说，本文算法相比较于其他两种算法，局部细节保留更好，并未出现明显失真现象，有效解决了He算法[2]中的块状效应.

图4 主观分析去雾效果Fig.4 Subjective analysis of defogging effect

图5 改进算法和原算法局部放大图对比Fig.5 Comparison of local magnification of two algorithms

4.3 客观指标评价

本节从信息熵[17]、峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)[18]和结构相似性(Structural Similarity,SSIM)[19]3方面对下面9张浓雾图像进行定量分析，实验结果如图6所示.从上至下每一行的雾浓度呈递增趋势，以丰富该算法对不同的实验条件的效果和影响,验证该算法的适应程度.

图6 定量分析去雾效果Fig.6 Quantitative analysis of defogging effect

信息熵[17]是对图像信息量的度量，来评价图像质量的好坏，信息熵越大，则说明图像包含信息量越高，图像复原质量越好，信息熵公式为：

(14)

其中，pi是像素值i出现的概率.图6的信息熵值如表1所示，G-SVD得到的复原图像信息熵平均值最高，相比较于原暗通道去雾算法[2]信息熵提升了0.26，而和Wang算法[16]相比高出约0.07.

峰值信噪比[18]是通过对比纯净图像I和噪声图像K，衡量纯净图像的重建质量方法，如公式(15)所示：

(15)

其中MSE表示为均方误差：

(16)

MSE越小，PSNR越大，则图像失真越小，图像质量越高，如表2所示，图6的测试图像在本文算法中PSNR平均值高于其他两种算法.其中，本文算法相较于He算法和Wang算法PSNR值提高了近4.4，大大的提升了去雾图像的能见度，且去除了冗余噪声.

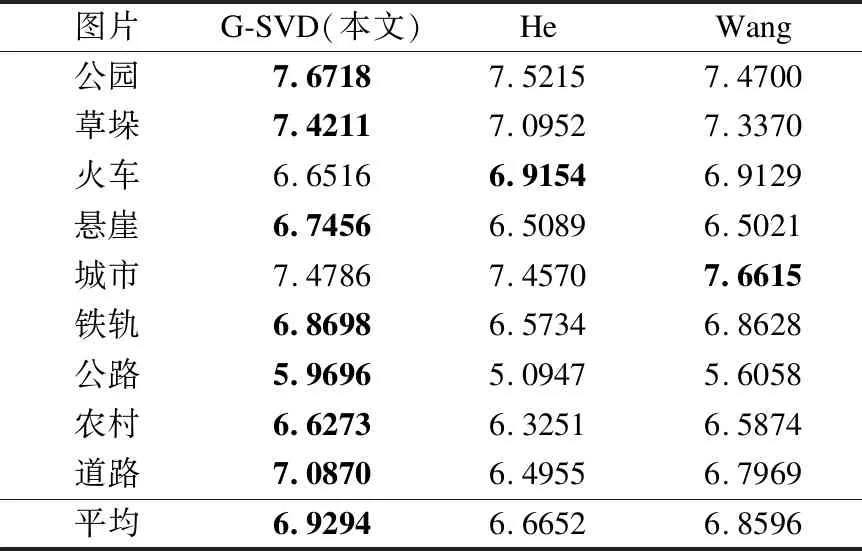
表1 不同算法的信息熵Table 1 Information entropy of different algorithms

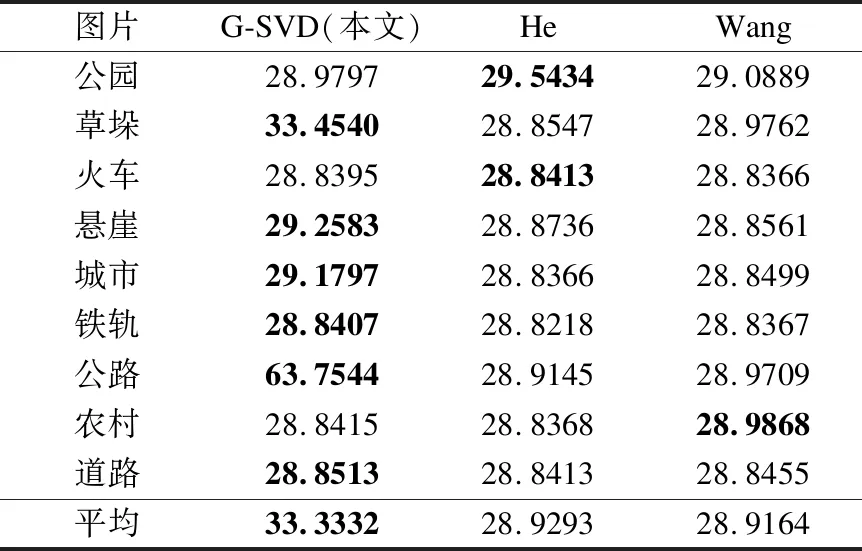
表2 不同算法的峰值信噪比(PSNR)Table 2 PSNR of different algorithms

结构相似性[19]用于评价图像结构信息的保留程度，可以解决PSNR和MSE无法衡量图像结构相似的问题，如公式(17)所示：

(17)

其中μx和μy表示图像的X和Y的亮度均值，而σx和σy表示图像X和Y的标准差，C1和C2为常量.SSIM越大表示图像去雾效果越好，原图重要信息保留程度越高.结果如表3所示,本文算法的SSIM平均值分别高于其他两种算法0.15和0.3.

综合上述3项指标，可以认为提出的算法在信息保留、重建图像质量和结构信息的保留程度上，比其他两种方法效果更优秀，适应性更强，同时，在处理浓雾效果中，也仍保留了较多的细节，并有效的避免了He算法中的块状效应以及Wang算法中的图像失真和颜色畸变.

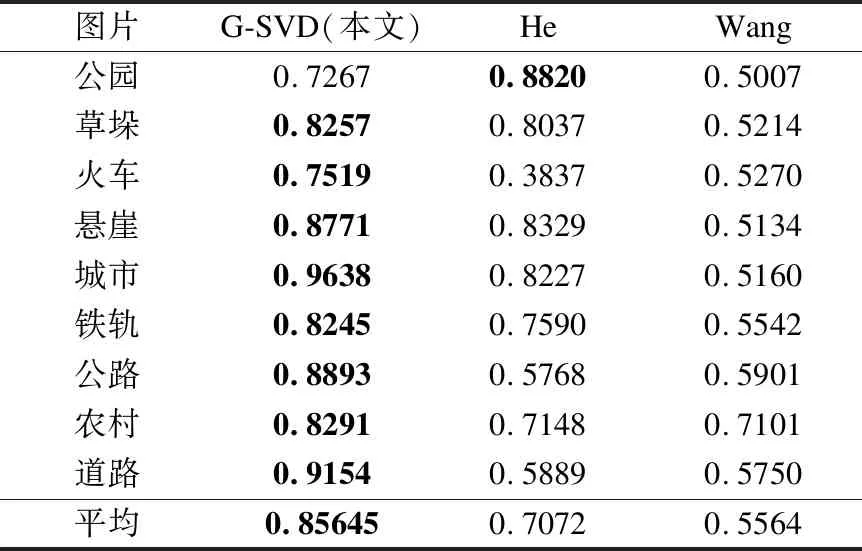
表3 不同算法的结构相似性(SSIM)Table 3 SSIM of different algorithms

4.4 算法速率分析

表4给出不同去雾算法对各个尺寸的所耗费时间对比.从各算法执行时间可以看出，本文算法G-SVD在像素范围为240×210-600×450的图像处理效率均高于其他3种算法(Chen[11]、Tarel[20]和Meng[21])，但是随着尺寸的增大至800×600时，本算法的耗时则高于Chen和Meng算法.分析其原因在于本文算法需要对图像进行滑动窗口处理，遍历图像所有像素点，因此导致算法时间复杂度高于其他两种算法.此外，由于本文算法还需对图像进行SVD矩阵运算，这也间接导致算法耗时的增长量高于其他算法.简化矩阵运算，降低算法的时间复杂度，这也将成为下一阶段的研究方向及重点，以应用在视频处理中[22].

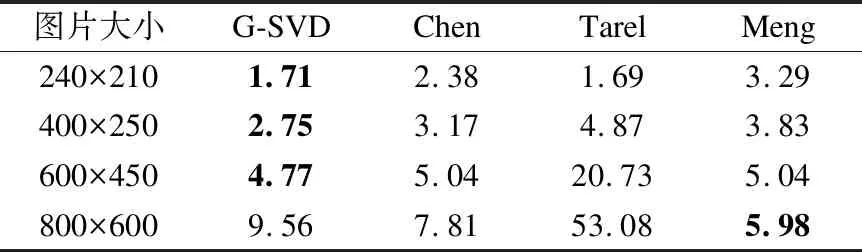
表4 不同算法的耗时对比(时间单位：秒)Table 4 Time consuming comparison of different algorithms(time unit：s)

5 总 结

本文提出了G-SVD去雾算法，它采用基于滑动窗口的高斯卷积来预估各个像素点的环境大气光，并引入偏差系数提高去雾图像亮度，再采用奇异值分解去除冗余噪声，从而有效的去除原暗通道去雾算法的块状效应，并通过信息熵、PSNR和SSIM3个方面定量分析该算法的提升.实验结果表明，G-SVD算法可以有效去除块状效应且浓雾处理效果较为理想.但是该算法的去雾结果仍然存在着细节模糊、部分色彩失真等缺陷，此外，随着图像尺寸增大，算法时间复杂度较大等弊端也显现出来，这将成为未来研究的主要方向.而随着人工智能、5G通信等技术的发展，下一步也将去雾算法进一步改进，融合实时视频传输[23]等技术，实现实时去雾.