搜索空间自适应量子搜索算法

谢旭明，段隆振，邱桃荣，康小丽

1(南昌大学 信息工程学院，南昌 330031) 2(南昌大学 图书馆，南昌 330031)

1 引 言

量子计算最早由Feynman[1]提出，此后不少学者提出了不同的量子算法.其中Shor[2]提出的大数质分解量子算法和Grover[3]提出的无序数据库量子搜索算法是最为经典的两个量子算法.Shor提出的大数质分解量子算法相对于经典算法实现了多项式级别的加速，但这个算法目前看来只能针对这类特定的问题；而Grover算法，因其解决的搜索问题可应用于许多机器学习算法中，得到了更为广泛的关注和研究.

Grover算法是由L.K.Grover于1996年提出的.自提出以来，许多学者对其进行了进一步的研究，主要方面有：经典计算下的难点问题、与机器学习相结合、以及算法自身的改进等.

Grover算法能够处理以前难以解决的或加速需要大量计算的问题.孙国栋等人[4]将Grover算法应用到求根问题上，将求根问题的计算复杂度降低到原来的平方根.朱皖宁等[5]用Grover算法来识别Weblog中的用户，相较于经典计算，改进策略将搜索的查询复杂度进行了二次加速.Indranil等[6]先将Grover算法的黑盒添加上动态选择的功能，然后将改进算法用在推荐系统上.杨婕等[7]先将Grover算法与量子计数相结合，提出一种量子黑箱线路设计方案，然后将提出的方案应用于BLAKE算法的安全性分析中.

Grover算法，因其适用性，也可以用来改进很多机器学习算法的一些子程序，进而达到对原机器学习加速的效果.阮越等[8]将Grover算法引入到主成分分析算法中，设计了一种人脸编码方案，进一步压缩了降维处理后的特征空间.Yu等[9]，通过改进Grover算法来求解频繁项集，实现了关联规则挖掘的量子化.He等人[10]将经典量子搜索黑盒改进为可以同时接受候选特征集及特征索引的黑盒，实现了特征抽取的量子化.周晓彦等人[11]借助量子搜索的思想对k-means算法进行量子化处理.

为了提高Grover算法的成功概率，不少学者也进行了相关的研究.这方面的研究主要集中在改进算子的相位旋转角度.Li等[12]将相位角度改为0.1π，Zhong等[13]将相位角度改为1.018，Younes等[14]将相位角度改为1.92684π.这些改进策略使成功概率均获得了提升.

在已见的Grover算法改进策略中，大多数是围绕着改变算子的相位角度来进行的，但这些策略的一个致命缺点就是迭代次数不好确定.为解决这个问题，本文提出一种搜索空间自适应的量子搜索算法，拟在不改变迭代次数计算方法的基础上，提高算法的成功概率.

2 Grover算法及其缺陷

2.1 Grover算法

Grover算法首先要准备n个|0>态的量子位，并通过n个Hadamard门构造一个n量子位的等权重叠加态，然后以一定的次数将U算子作用于n量子位，最后测量这n个量子位.U算子包含两个子算子Ua和Us：Ua算子又称为量子黑盒，用于实现目标分量的相位取反；Us算子用于实现目标分量取反后叠加态的均值翻转.

Grover算法的运算过程在Hilbert空间中的表示如图1所示.

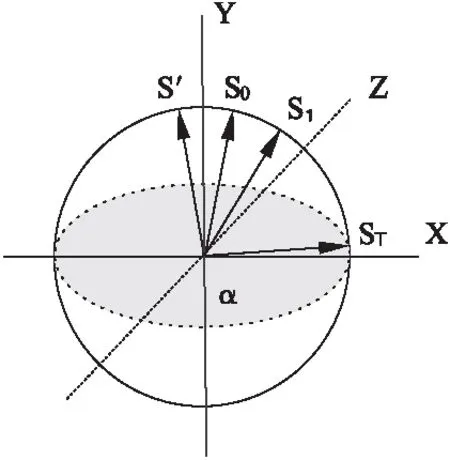
图1 Grover算法在Hilbert空间的表示Fig.1 Grover algorithm in Hilbert space

图1中，目标分量值平面α由X轴与Z轴确定.Y轴表示α的垂直分量.s0是初始的等权重叠加态，s′为经过Ua算子作用后的叠加态，s1为s′经过Us算子作用后的叠加态，sT为T次迭代后的叠加态.Grover算法的基本思想就是将与目标分量值平面α夹角较大的叠加态s0经过一系列的幺正变换转变为与α夹角较小的sT，此时目标分量的概率幅值较大.

设Tpft是理论上算子的迭代次数，这个值大部分情况下是小数，在现实中是不可能出现小数次的迭代次数的.而T是算法的实际迭代次数，是一个正整数，是对Tpft四舍五入取整后的值.T的表达式如公式(1)所示，其中round()为四舍五入取整函数.Tpft的表达式如式(2)所示.

T=round(Tpft)

(1)

(2)

(3)

2.2 Grover算法的缺陷

结合式(1)-式(3)，成功概率P与目标分量λ的关系可以绘出图2.

2005年，“北京DRC工业设计创意产业基地”规划投建，为中国工业设计带来全新的元素与升级。基地中搭建起“逆向工程实验室”“3D打印体验馆”“设计博物馆”等一系列创意空间；同年，“光华龙腾奖.中国设计十大杰出青年”评选启动，为中国设计行业发掘中国力量；2006年，“中国设计红星奖”设立，助力中国设计走出国门，在国际化征途中完成设计服务业和制造业的融合与蜕变；2008年，以北京奥运为契机，“奥运设计”的理念走进社区，走进人们生活，这一年，深圳成为全球第六个世界“设计之都”。

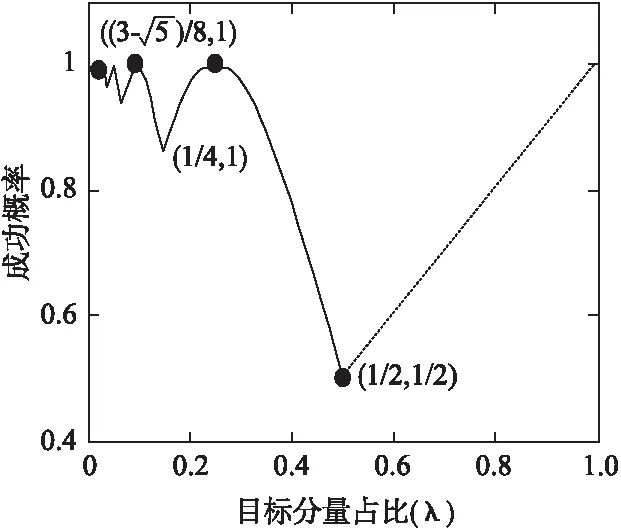
图2 经典Grover算法成功概率Fig.2 Success rate of the classic Grover algorithm

3 改进的量子搜索算法

当目标分量占比很小的时候，量子搜索算法总能以较高的概率得到目标分量；当目标分量占比较大的时候，算法得到目标分量的概率就不那么高.因此，该研究只需要改进目标分量占比较大的情况.本文拟采用扩大搜索空间的方式来提升目标分量的概率幅.但随着搜索空间的增大，算法的计算复杂度也会提升，因此，我们必须将搜索空间在合适的范围内扩大.下面我们先提出几个定理，再给出具体的改进策略.

3.1 定理证明

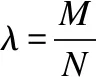
证毕.

证毕.

证明：结合定理1和定理2，很容易得出.

证毕.

定理3.当T越大时，目标分量概率的极小值越大.

证毕.

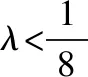
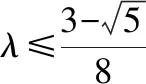
证毕.

3.2 改进策略

(4)

4 算法效率分析

该研究将提出算法与经典Grover算法的效率进行了比较.比较结果如图3所示.

图3 成功概率比较图Fig.3 Comparison of success rates

5 结 语

通过自适应地改变不同目标分量占比时的搜索空间，本文整体上实现了成功概率的提升.该策略可以沿用经典Grover算法的思路来求解算子的迭代次数，避免了以往通过改变算子旋转相位策略的缺陷，在实施方面有更好的可操作性.