预制钻孔煤样冲击倾向性及能量耗散规律

王爱文，高乾书，潘一山，宋义敏，李 岚

(1.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000; 2.辽宁工程技术大学 冲击地压研究院，辽宁 阜新 123000; 3.北方工业大学 土木工程学院，北京 100144; 4.中煤科工集团沈阳设计研究院有限公司，辽宁 沈阳 110015)

钻孔卸压由于具有操作便捷、成本低廉、可快速解危等优点，被视为防治冲击地压常用措施[1-2]。钻孔卸压的防冲效果受到煤岩力学特性、钻孔孔径、钻孔深度、钻孔布置等参数影响，确定合理的钻孔卸压参数是冲击地压防治的关键。

长期以来，国内外学者对钻孔煤岩体应力分布、位移演化规律、钻孔卸压参数优化、钻孔卸压效果评估等进行了大量研究[3-15]。ZHAO等[3]应用物理模型及声发射技术研究预制圆形孔洞岩石的断裂演化，得知在平行于加载方向产生拉伸劈裂裂纹，在孔两侧产生压缩裂纹。QIAN等[4]研究预制不同裂隙角度、岩桥长度的砂岩破裂特征，得到力学参数随预制缺陷变化规律，初始裂纹类型和裂纹扩展模式。WU等[5]使用DIC方法对5种形状的预制钻孔试样进行监测，得到不同类型试样的裂隙发育扩展及应力分布规律。LIN等[6]针对不同类型孔径、分布、间距的预制孔花岗岩试样的裂纹萌生、聚结机理及破坏行为进行了研究。刘金海等[7]采用室内实验方法，给出确定钻孔间距、钻孔直径的方法，提出强排煤粉的主要作用是“降模增变”和“耗能增阻”。贾传洋等[8]通过对孔径、孔间距及孔深等参数进行实验研究，指出裂纹扩展贯通导致的应力释放是钻孔产生卸压作用的根本原因。易恩兵等[9]通过采用数值模拟对软及硬煤层的大直径钻孔卸压效果进行了研究，发现软煤层中实施钻孔卸压效果较好。齐燕军等[10]开展含预制卸压孔煤柱相似试验，发现卸压孔孔径对卸压效果具有显著的尺寸效应。张强等[11]采用数值计算方法，得到了深部高应力花岗岩钻孔卸荷后形成的应力集中区沿深度变化的规律。

上述研究，一方面从裂隙发育角度研究不同类型预制钻孔煤岩样的表面变形破坏规律，另一方面从应力的角度研究钻孔对煤岩体应力的改变规律。实际上，卸压钻孔不仅会改变煤岩体的变形规律、应力分布状态，同时也会改变煤岩体结构及其冲击倾向性，因此研究含孔洞煤样的冲击倾向性及能量耗散规律对分析卸压钻孔防治冲击地压机制具有重要意义。

煤岩受载破坏实际上是能量输入与耗散的过程，文献[16-20]基于能量理论对各类煤岩受载状态时的能量演化规律进行了大量研究，但未考虑卸压钻孔对能量演化规律的影响。对于钻孔煤岩样，受载破碎后的破碎颗粒分布特征除了与其属性、受载类型相关还与钻孔数量以及布置方式有关，分形维数可以用于反映煤岩受载破碎程度[21-24]。笔者引入分形理论研究预制钻孔煤样受载破碎颗粒的分布特征，进而讨论钻孔卸压对煤样能量演化规律的影响。

笔者通过对4种钻孔布置方式的煤样进行单轴抗压强度、动态破坏时间、冲击能量指数、弹性能量指数的测试试验，分析试样的宏观破坏特征及其冲击倾向性的变化规律。利用分形理论进行试样的破碎程度分析，寻求破碎颗粒表面积与分形维数的相关关系及破碎颗粒新增表面积与峰后能量释放和能量耗散之间的相关性，进一步揭示钻孔卸压作用原理，期望为优化钻孔卸压参数提供基础理论依据。

1 试样制备及试验方案

1.1 试样制备

鉴于真实煤样自身具有丰富的裂隙、层理等结构特征，选用原煤制备的试样进行钻孔卸压试验，试验结果离散性较大，为了排除钻孔因素外的其他因素影响及保证试验结果的可重复性，试验样品制备采用相似材料。

以大同矿区某矿所取的具有弱冲击倾向性煤样为原样，根据相似理论，采用水、石英砂和水泥比例为1∶1.4∶2的均质混合物制成50 mm×50 mm ×100 mm尺寸的标准试样进行煤样的模拟[12]。

根据现场环境及煤体力学性能，确定几何相似常数为20。试样分为完整无钻孔(VIII)，单列单排钻孔(C3)，单列双排钻孔(C4)和单列三排钻孔(A5)4种类型(后文中分别称为完整试样、单孔试样、双孔试样、三孔试样或用字母表述)。钻孔布置以试样表面形心为中心点，垂直布置2列钻孔间的距离为50 mm，水平布置2排钻孔间的距离为30 mm。选用8 mm直径的不锈钢圆柱按照钻孔布置图(图1(a))在试样分层压实后插入其中，并在固化过程中移除圆柱来模拟现场使用150 mm直径钻头形成的大直径卸压钻孔。养护结束后将试样表面打磨平整，完成试样的制备。测量记录各试样尺寸、质量、密度后进行试验。

典型应力应变(ε-σ)、时间载荷(t-P)曲线对比如图2所示，原煤与配比完整煤样的单轴抗压试验所得力学参数见表1。结合图2、表1中2类曲线可知2种材料应力峰前压密变形阶段具有较好的一致性，峰值强度相近，峰后应力跌落过程较为一致，因此可认为选用的相似材料能较好地体现出煤样的力学性能，进而可用于钻孔卸压煤岩体的力学特性研究。

图1 钻孔布置及试样示意Fig.1 Drillhole layout and sample schematic diagram

图2 原煤与相似材料试样应力应变、时间载荷曲线对比Fig.2 Comparison of stress-strain and time-load curves between coal sample and similar materials sample

表1 试样力学参数Table 1 Mechanical parameters of sandstone samples

1.2 试验方案

试验系统如图3所示，加载过程中使用相机采集试样变形破坏图像。将压力传感器与动态应变仪连接进行动态破坏时间的测量，动态应变仪的采样频率设置为1 kHz。通过事先对各系统时间的校准统一以及试验开始同时进行采集，保证各采集系统在时间上的对应。各个试样加载结束后收集加载台上的破碎颗粒，以便后续的计算处理。

图3 试验、监测系统Fig.3 Test and monitoring system

4种钻孔布置方式的煤样按照国家标准[13]中的规范进行冲击倾向性4项指数的测试试验并对每个指数均取至少3个有效数据。笔者在进行冲击能量指数(KE)测试时采用0.01 mm/min的加载速率，进行单轴抗压强度(RC)、动态破坏时间(DT)和弹性能量指数(WET)的测试，均采用0.5 MPa/s的加载速率，其中进行弹性能量指数测试时采用循环加卸载、逐级增加载荷直至破坏的形式。

2 试验结果

2.1 冲击倾向性变化规律

典型4种钻孔布置方式的煤样，破坏前后形态如图4所示。可以看出，完整试样以剪切劈裂破坏为主，在平行加载方向形成贯穿裂纹，裂纹较为单一;单孔试样在钻孔附近起裂扩展，沿剪切面产生贯穿裂纹，并产生次生裂隙;双孔试样裂隙发育融合集中在钻孔间的岩桥内，多形成垂直贯穿裂纹，并出现塌孔;三孔试样岩桥间的裂隙较为发育，塌孔现象较显著。

图4 典型试样破坏特征Fig.4 Typical sample failure characteristics

4种钻孔布置类型煤样的4项冲击倾向指数完整测试结果见表2，典型测试曲线如图5所示。图5(a)为典型单轴抗压强度RC测试曲线，完整试样峰值应力、应变最大，分别为22.30 MPa,0.009 3，三孔试样峰值应力、应变最低，分别为12.82 MPa,0.001 9。较完整试样，随钻孔排数增多峰值应力、应变逐渐降低，说明钻孔试样抵御变形、积聚弹性应变能的能力逐渐减弱。

表2 冲击倾向性指数测试结果Table 2 Test results of bursting liability index

图5 冲击倾向指数典型测试曲线Fig.5 Typical curves of bursting tendency index test

图5(b)为典型动态破坏时间DT测试曲线，DT表示从极限强度至完全破坏所历经时长。DT与RC是同一试样测试时由动态应变仪和伺服压力机系统分别记录的时间、载荷等数据经计算后得到的。由图5(b)可知完整试样应力峰前的耗时最长、峰后的耗时最短，分别为56 566，1 231 ms，三孔试样峰前的耗时最短、峰后的耗时最长，分别为30 400，2 423 ms。结合图5(a)可知，随钻孔排数增多，钻孔试样的应力峰前塑性增强，峰后裂隙扩展速率降低，脆性减弱，动态破坏耗时延长。

图5(c)为典型冲击能量指数KE测试曲线，KE表示试样应力峰前积聚变形能与峰后耗散能量的比值。对比图5(a)可知，二者加载方式虽有差异，但均体现出随钻孔增多峰值强度逐渐降低的规律。由于KE测试加载速率慢，微裂隙发育更为充分，致使图5(c)更显著地体现出弹性模量逐渐降低的趋势。试样峰后阶段变形逐渐增大，说明低加载速率时，钻孔试样的塑性增强更为显著，这与文献[14-15]研究结果相符。随钻孔排数增多，应力峰前积聚弹性能逐渐降低、峰后耗能升高，冲击能量指数降低。

图5(d)为典型弹性能量指数WET测试曲线，图中为加卸载的应力应变曲线，WET表示加卸载应力-应变曲线下积聚弹性变形能与塑性耗散能的比值，WET越大表示单次加卸载后储存的弹性变形能远大于在此过程中耗散的能量[16-20]。图5(d)中完整试样WET值最大为3.91，随钻孔增多，WET值逐渐降低，三孔试样最低为1.85。这表明随钻孔增多，钻孔试样加卸载后塑性增强，且循环加卸载使得钻孔周围裂隙发育丰富、损伤增强、耗散能量提升、储存能量降低，弹性能量指数逐渐降低。

冲击倾向性4项指数测试结果、均值变化曲线分别如表2、图6所示。较完整试样，钻孔试样的单轴抗压强度RC、冲击能量指数KE、弹性能量指数WET均逐渐降低，动态破坏时间DT逐渐升高，其中三孔试样较完整试样的4项指数分别降低21.6%，49.5%，46.1%，提升152.8%。参照鉴定标准[13]，体现出钻孔试样的冲击倾向性逐渐降低，说明卸压钻孔能够降低煤体冲击倾向性。

图6 冲击倾向指数均值变化曲线Fig.6 Average change curves of bursting liability index

由图6可知，RC，KE，WET之间呈正相关性，3者与DT呈负相关性，其中表征弹塑性变化的KE,WET变化趋势较为一致，体现出试样随钻孔增多塑性增强，同时说明弹塑性的变化是影响煤样发生突然破坏的重要因素，而钻孔卸压对于弹性变形能力的削弱，塑性变形能力的提升均与裂隙发育程度相关。裂隙的发育程度同时决定了岩样破坏后的颗粒破碎程度，因此破碎颗粒特征同样能够反映出钻孔卸压的作用效果。

2.2 破碎颗粒分形特征

岩石破碎颗粒具有丰富的信息，被常用于研究岩石受载特性，其中应用较广泛的是破碎颗粒分形维数及破碎颗粒表面积。利用破碎颗粒的质量-等效粒径进行分形维数D的计算，计算公式[21-24]为

D=3-α

(1)

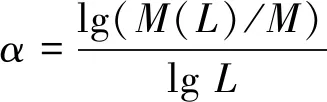
(2)

式中，α为lg(M(L)/M)-lgL双对数坐标下的斜率值;L为统计区间等效粒径特征尺寸;M为破碎颗粒总质量;M(L)为等效粒径小于L的破碎颗粒质量。

对收集的试样破碎颗粒进行筛分、称重测量，并按式(1)，(2)计算。选用的分级筛孔径从小到大依次为:0.075，0.250，0.50，1.00，2.50，5.00，10.00 mm，而尺寸>50 mm的颗粒，则使用游标卡尺多次测量取均值并称重记录。

图7为典型双孔试样破碎颗粒多粒径筛分分布图，由图可以看出粒径>10 mm的破碎颗粒数量较少，尤其是粒径>50 mm的破碎颗粒仅有3块。表3为典型4类试样破碎颗粒筛分后在各特征尺寸区间内的质量分布，图8为表3对应的分形曲线。图8(a)为整体特征尺寸分形维数拟合曲线，图8(b)为去除0.075 mm特征尺寸及10 mm以上特征尺寸破碎颗粒分形维数拟合曲线。

图7 典型筛分颗粒分布Fig.7 Distribution of typical sieved particles

对比图8可知:4种钻孔布置类型煤样在整体范围内的分形维数D分别由2.10，1.98，1.86，1.97升高为局部区域中的2.46，2.42，2.39，2.21，相关系数R2分别由0.903，0.866，0.787，0.914升高为0.996，0.988，0.984，0.970。局部区域中分形维数D、相关系数R2均有所升高且R2均大于0.96，故可认为局部范围内破碎颗粒分形特性更为显著。

结合图7，8与表3可知粒径>50 mm的碎块个数少、质量大，粒径<0.075 mm的颗粒质量小、误差大。局部范围内的分形维数D均大于整体范围且局部范围内的相关系数R2更高，说明上述两个区间内碎块对分形维数影响较大，这与许多学者[16-17]观测到的岩石碎块分布具有多重尺度下的自相似性，且自相似性不一定在整个块度范围内存在相符。为了统一计算分形维数，将分形上阈值设为30 mm，分形下阈值设为0.075 mm。

表3 冲击能量指数测试典型试样破碎颗粒质量分布Table 3 Mass distribution of broken particles in bursting energy index test

图8 典型试样lg(M(L)/M)-lg L曲线Fig.8 lg(M(L)/M)-lg L curves of typical sample

4种钻孔布置类型煤样进行冲击倾向性指标测试后的破碎颗粒，依上述计算方法，计算所得分形维数D的均值变化如图9所示。由于动态破坏时间和单轴抗压强度试验加载试样相同，故其分形维数D相同。

图9 各类型试验分形维数曲线Fig.9 Fractal dimension curve of various types of tests

分析图9可知:

(1)单轴抗压强度试验时，随钻孔排数增多，分形维数D整体呈现先上升后下降趋势，双孔试样D值最大、破碎程度最低。这可能与采取较快的加载速率以及钻孔垂直布置共同作用下，致使宏观主裂纹的分布形态差异相关。

(2)进行冲击能量指数、弹性能量指数试验时，由于加载缓慢或循环加卸载使试样内部裂隙发育充分，致使试样破坏后小粒径颗粒质量占比升高，体现出随钻孔排数增多，D值逐渐减小，破碎程度升高。由于裂隙发育多发生在岩桥之间，三孔试样岩桥数目多，导致三孔试样D值最小，破碎程度最高。

(3)结合图8，9可知，在选取的分形特征阈值范围内计算所得分形维数均大于2，说明在此区间内的大特征尺寸颗粒占比较少，试样破碎程度较高，破碎颗粒具有较好的自相似性，故可认为在此区间内不同等效粒径L的颗粒几何形状高度相似。

2.3 破碎颗粒比表面积及表面积

岩石破碎颗粒的分形特性表明:在一定分形特征尺寸阈值内具有较好的分形特征，则在此区间内的破碎颗粒具有较好的几何相似性，可将在该范围内破碎颗粒的几何形状视为相同类型。

假设破碎颗粒密度ρ均匀一致，则可利用规则几何体比表面积计算公式[25]，进行小尺寸颗粒比表面积的计算(表4)。由于0.075 mm粒径的破碎颗粒尺寸较小，产生误差大且质量较少，故其可忽略不计。对于特征尺寸>10 mm的破碎颗粒由于形状不规则，其表面积只能逐个测量得到，笔者采用图像测量方法[26-29]。假设破碎颗粒密度ρ均匀一致，将特征尺寸小于30 mm的颗粒视为规则几何体，则试样初始表面积、各特征尺寸破碎颗粒总表面积、新增表面积计算为

(3)

式中，ΔSa，Sa，So分别为试样新增表面积、破碎颗粒总表面积、初始表面积;SL，SR，ML，VL分别为特征尺寸为L的颗粒总表面积、比表面积、总质量、总体积。

表4 规则几何颗粒比表面积表达式Table 4 Calculation formula of specific surface area of regular geometric particles

由2.2节所述，特征尺寸在分形上阈值30 mm、分形下阈值0.075 mm之间的破碎颗粒具有良好的自相似性，则可将特征尺寸为0.25，0.5，1.0，2.5，5.0，10.0 mm的破碎颗粒视为同类型规则几何体，如球体、椭球体、正四面体、正立方体等，进而对颗粒比表面积、表面积进行计算，图10为规则几何体示意图。

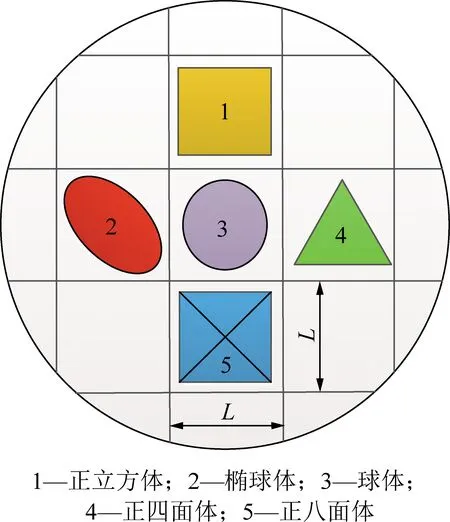
图10 规则几何体颗粒示意Fig.10 Schematic diagram of regular geometric particles

破碎颗粒的特征尺寸L与规则几何体棱长L1的关系及化简后的比表面积计算公式见表4。由表4中各类比表面积计算公式分析可知:各类型颗粒的比表面积只与材料密度、颗粒粒径相关。同一形状颗粒的材料密度相同时，颗粒粒径越大其比表面积越小。不同形状颗粒在具有相同材料密度、颗粒粒径时，比表面积大小关系为:椭球体<球体=正立方体<正八面体<正四面体。在质量M相同时，由于不同形状的颗粒计算结果差异较大，为降低误差，本文选用比表面积最小的椭球模型用于特征尺寸小于30 mm颗粒的表面积计算[25]。

笔者采用图像测量法[28-29]对特征尺寸大于10 mm的破碎颗粒进行表面积测量。图像测量法是基于定量体视学原理，将破碎颗粒视为不规则柱体，采用图像二值化方法得到破碎颗粒的投影柱面面积、投影面周长，并结合其柱体厚度计算其表面积，见公式(4)。图11为典型双孔试样大粒径破碎颗粒，图12为部分破碎颗粒运用Matlab程序进行黑白二值化处理前后的对比图。

(4)

式中,Si,hi,SP,Sk,CP,Ck分别表示各个颗粒的表面积(mm2)、厚度(mm)、投影面积(mm2)、投影二值化像素面积(dpi2)、投影周长(mm)、投影二值化像素周长(dpi);k为面积换算系数(mm2/dpi2);l为长度换算系数，mm/dpi;hi由游标卡尺多次测量取均值，k,l由多个已知尺寸的标尺依据式(4)计算并取均值。

图11 典型试样大粒径破碎颗粒Fig.11 Large diameter broken particles of typical sample

图12 图像测量示意Fig.12 Schematic diagram of image measurement

图13为使用椭球形模型计算小粒径颗粒表面积及使用图像测量法计算大粒径颗粒表面积得到的典型四类钻孔布置煤样的各特征尺寸破碎颗粒累计表面积柱状图。由图13可知:① 大粒径颗粒表面积占据80%以上，不同特征尺寸的破碎颗粒表面积分布规律相近，在特征尺寸小于10 mm时尤为显著。② 特征尺寸大于10 mm的颗粒表面积占比较大，而大粒径颗粒的形成一般在峰后伴随宏观主裂隙的扩展，说明应力峰后阶段耗散大量能量，这与单轴抗压试验应力峰后破裂加剧，耗能突增相符。

图13 钻孔卸压典型破坏试样各粒径颗粒表面积Fig.13 Surface area of particles with different diameters of typical failure samples

2.4 钻孔卸压试样破碎颗粒特征

岩石加载直至破坏过程中能量耗散伴随着微裂隙的萌发、扩展、连通及宏观裂纹的产生，随之形成不同粒径的破碎颗粒，产生新的自由表面。因此，破碎颗粒表面积与分形维数对于岩石破碎分析具有相同作用，但新增表面积对研究能量耗散更具价值。

钻孔排数对破碎颗粒的质量分布、分形维数与表面积均有不同程度影响。本文以进行单轴抗压强度测试的试样为破碎颗粒特征分析对象。图14(a)为特征尺寸为L的颗粒质量mi与破碎颗粒总质量M的百分比Wi，以及在区间0.25～10 mm破碎颗粒总质量mt与破碎颗粒总质量M的百分比Wt的变化曲线，图中纵坐标W表示Wi或Wt。图14(b)为分形维数散点及均值曲线。图14(c)为大粒径颗粒表面积、小粒径颗粒表面积、破碎颗粒新增表面积及均值曲线。图14(d)为4种钻孔布置煤样破碎颗粒的分形维数均值与图14(c)中3类面积均值之间的线性拟合。分析可知进行单轴抗压强度测试时:

(1)随破碎颗粒特征尺寸减小，其Wi值逐渐降低。特征尺寸相同时，4类试样的Wi值的大小排序为三孔试样>完整试样>单孔试样>双孔试样，同时Wt值与Wi值变化规律相同，说明双孔试样在粒径为0.25～10 mm区间内的破碎颗粒质量占比最小，这与表3中颗粒质量分布占比相符。

(2)破碎颗粒分形维数D的均值呈现出先增大后降低的趋势，即三孔试样<完整试样<单孔试样<双孔试样。双孔试样D均值最大为2.45，三孔试样D均值最小为2.33，说明单轴抗压强度测试时三孔试样破碎程度最高，双孔试样破碎程度最低，这与图14(a)中三孔试样Wt值最大、双孔试样Wt值最小的结果相符。结合典型试样破坏图4进行分析可知，出现这种现象的原因可能与加载速率较大以及钻孔垂直布置共同作用下产生的宏观主裂纹分布形态差异相关。完整试样形成贯穿主裂纹后由于裂纹间的啮合作用，仍会保持一定的承载能力，直到次生裂纹不断发育，导致试样最终承载失效。次生裂纹发育过程中会产生一定数目的小粒径颗粒。单孔试样在钻孔因素作用下，由钻孔上下两侧起裂并形成贯穿主裂纹，随着加载持续，同样会产生次生裂隙，直至失去承载能力。双孔试样在钻孔上下均形成起裂裂纹，当两钻孔间的微裂隙汇合形成宏观裂纹后试样破坏，这种孔间贯穿裂纹往往和钻孔周围形成的裂纹产生组合效应，即在从钻孔至试样端部的区域内产生U形破裂。这种破裂形式往往会形成较大的楔形破碎块(图11)，导致双孔试样破裂后基本失去了承载能力，进而减少了小粒径破碎颗粒数目。较双孔试样，由于三孔试样上下钻孔边缘至试样端部距离更短，导致在该区域裂隙更为发育，破碎严重，甚至产生塌孔现象。且由于钻孔数目增多，三孔试样钻孔间的裂隙更为发育，这导致三孔试样小粒径破碎颗粒质量占比最大[14-15]。

图14 试样破碎颗粒特征Fig.14 Broken particle characteristics of samples

(3)将特征尺寸>10 mm颗粒的表面积称为大粒径颗粒表面积，其余称为小粒径颗粒表面积，表面积增大表示试样破碎程度升高。由图14(c)可知较完整试样，3种颗粒总表面积随钻孔排数增大均呈现出先减小后增大的趋势，双孔试样均为最小值，三孔试样均为最大值。表明双孔试样破碎程度低，三孔试样破碎程度高,这与分形维数描述的破碎规律相符。

(4)由图14(b)，(c)中均值数据可得到图14(d)中颗粒表面积与分形维数的相关曲线。所得3项拟合关系的相关性系数R2均>0.8且斜率均为负值，可知分形维数与三种颗粒表面积均具有较好的负相关性。其中分形维数与大颗粒面积相关性系数R2最大为0.934，说明二者相关性更为密切。分形维数越小则3种颗粒表面积越大、试样破碎程度越高，与实际相符。

3 新增表面积与能量耗散相关性

3.1 能量耗散计算方法

图15(a)为单轴压缩试验时，典型试样的应力-应变曲线。图15中，σc为峰值应力;σr为残余应力;E为峰前弹性模量;λ为峰后软化模量[30]。若全程外力做功大小由加载曲线和横坐标轴所围不规则图形面积确定，即为Φe+Φd+Φe1+Φd1。Φe为应力峰前阶段储存的弹性应变能(由E计算)；Φe1为峰后阶段残余弹性应变能(由λ计算)；Φd为峰前耗散能，Φd1为部分峰后耗散能；Φe+Φd1为累计峰后耗散能。则任意时刻能量可由公式(5)求得。

(5)

其中,Ut，Uet，Udt，Et分别为任意t时刻的总应变能密度、弹性能密度、耗散能密度和弹性模量。t1时刻分别记为Ut1，Uet1，Udt1，Et1;t2时刻分别记为Ut2，Uet2，Udt2，Et2;峰前弹性模量用Et表示，峰后弹性模量用λt表示。

图15 岩石破坏过程能量演化规律Fig.15 Energy evolution law of rock failure process

图15(b)中为单轴抗压试验典型应力-应变曲线，及由式(5)中能量计算方法得到的Ut∝ε与Et∝ε曲线，分别表示各点弹性模量Et曲线、弹性能密度Uet曲线，其中A，B，C，D分别代表4个典型时刻的应力状态，各状态参数值见表5。

结合图15(b)及表5可知:A点为Et峰值点，可认为A点之前为岩石原生裂隙不断压密的线弹性阶段，在A点后岩体开始出现塑性区域;在A～B状态之间岩石局部塑性软化，使得弹性模量逐渐降低;B点为应力峰值点也为Uet峰值点，同时Et位于0值附近，说明此时塑性区已充分扩展，微裂隙充分发育;较B点，C点处应力降低0.32 MPa，但Et及Uet大幅度降低，表示在B～C阶段大量裂隙汇合扩展，消耗大量弹性应变能，岩石进入微裂隙快速扩展、汇合阶段，

表5 4种应力状态参数Table 5 Four stress state parameters

导致C点后快速的应力跌落，形成宏观裂纹。随着不断加载部分裂隙逐渐被压密，岩石恢复部分弹性，最终处于D点残余应力状态。

文献[31]给出了冲击地压发生的能量判据

δπ=0，δ2π≤0

(6)

U+A1+E1-R>0

(7)

式中,π为系统势能泛函;δ为一次变分;δ2为二次变分;U为应变势能;A1为外力功;E1为流动势能;R为破坏耗能。

图15结合式(6)，(7)可知:图15(b)中ε-σ曲线应力峰值(B点)储存的弹性应变能最大，对应于式(6)中的临界状态，即该点前不会引起破坏，该点后若任一点(C点)能量状态若满足式(7)则会引起破坏。

根据热力学原理，能量耗散是单向不可逆，能量释放是一定条件下双向可逆的。因此，忽略流动势能，根据式(5)可知:从峰值t1时刻到峰后任一时刻t2区间内，式(7)中各能量可由式(8)表示，式(8)中取t2为残余应力状态时(图15(b)中D点)得到的能量变化则可用式(9)表达。由能量判据及上述公式可知:降低应力峰前储存的弹性应变能Uet1、降低峰后能量ΔU、提升耗散能量ΔUd对防止引发动力响应均具有重要作用。

(8)

(9)

实际现场环境中的围岩系统受载主要为长期静态载荷及瞬时动态载荷，但能量大都源于岩层势能做功。当岩层瞬间释放大量能量ΔU时，若围岩系统静态破坏所能消耗的极限能量UR>ΔU时，则会避免引发动力破坏。由于瞬时动态载荷释放的能量难以预知，因此如何降低围岩系统应力峰前储存的弹性应变能Uet1或是提升峰后耗散的能量ΔUd具有实际应用价值。

降低Uet1即削弱岩体抵御变形的能力。提升ΔUd如式(10)所示:ΔUd主要包括裂隙发育扩展产生的表面能Ua，塑性变形能UP，动能Uk，热能Un，声电磁辐射Us。热能、声电磁辐射能量较小，塑性变形能与岩体原始构造相关，且为了降低动能Uk，故提升表面能Ua较为关键。由断裂力学可知表面能Ua计算方法如式(10)[32]：

(10)

其中，GIC为单位表面能;ΔSa为新增自由表面面积;KIC为断裂韧性。GIC由岩体自身性质决定，故提升新增自由表面面积ΔSa与升高表面能Ua呈正相关性，同时也与提升耗散能量密度ΔUd呈正相关性。

3.2 新增表面积与能量状态

单轴压缩试验的应力峰值时刻具有最大弹性应变能，随后裂隙扩展融合形成宏观裂纹，增大自由表面能同时消耗大量能量，并削弱岩石抵御变形能力，直至残余应力阶段恢复部分弹性。图16为单轴抗压强度测试时4种钻孔布置方式的煤样在峰值应力、残余应力时刻各项能量密度及该过程中能量演化差值与新增表面积的相关性曲线，各项能量密度计算方法由3.1节中所述。由图16分析可知:

图16 破坏前后能量演化曲线Fig.16 Energy evolution curve before and after failure

(1)较完整试样，随钻孔排数增多，应力峰值时刻的输入能量密度U1、耗散能量密度Ud1、储存弹性能密度Ue1均逐渐降低且趋于稳定，三孔试样能量密度降幅均最大，分别为36.7%，43.2%，27.9%。说明增多钻孔可以降低峰前积聚的能量Uet1，这证实了3.1节中提出如何避免引发动力破坏的方法是可行的，即钻孔卸压能够有效降低煤岩中储存的弹性能密度，但双孔、三孔试样能量密度差值不大，说明钻孔排数增加到一定程度后不会持续降低能量。

(2)与能量降低趋势不同，试样新增表面积ΔSa出现先减小后增大的“U”形变化趋势。其中三孔试样各类能量均最小，但其ΔSa较完整试样增大17.8%，表示应力峰前能量的输入、耗散与新增表面积无明显正相关关系。

(3)残余应力阶段，残余弹性能密度Ue2均较小，输入能量密度U2，耗散能量密度Ud2呈先减小后增大的“U”形变化趋势，与ΔSa变化趋势相近。其中三孔试样应力峰后阶段耗能与ΔSa陡增，说明峰后阶段能量输入、耗散与新增表面积呈正相关性。

(4)图16(c)中应变能密度为峰值应力状态与残余应力状态期间3类能量密度的变化差值。图中ΔU,ΔUd均为正值，ΔUe为负值，说明外力做功持续增加的输入能与峰值积聚的弹性能均转化为耗散能。ΔU,ΔUd与ΔSa均呈现“U”形变化趋势，且三孔试样均具最大值。ΔSa-ΔU,ΔSa-ΔUd关系如图16(d)中所示，分别呈幂次型、线性型关系，且相关系数R2均大于0.96，说明能量耗散与新增表面积具有良好的正相关性，这与式(10)中推论表达相符。结合2.4节中关于试样破碎颗粒特征论述，可知图16(c)中“U”形变化趋势和钻孔垂直布置及加载速率相关。

3.3 峰后能量释放、耗散速率

为了更好地对比应力峰后能量的变化规律，引入应力峰后能量释放速率Wer、能量耗散速率Wed两个指标，其计算公式为

(11)

其中，Wer为从峰值应力状态到残余应力状态，累积外力做功Ut2和峰前耗能Udt1的差值ΔUde与历经时间Δt的比值;Wed为峰后累积耗散能量ΔUd与历经时间Δt的比值。当试样残余应力为0，即残余应变能Uet2为0时，Wer，Wed二者数值相等。

应力峰值时刻单位时间内释放、耗散的能量越多，此时能量越易转化为动能，即引发动力破坏。由图17可知完整试样的Wer,Wed值均为最大，分别为125.4,122.9 kJ/(m3·s)，三孔试样均为最小，分别为36.6,36.0 kJ/(m3·s)。较完整试样，随钻孔排数增多，钻孔试样的Wer,Wed值均逐渐减低，二者降低幅值较为相近。单孔试样均降低约17.0%;双孔试样降低幅值更为显著，约为68.3%;三孔试样均降低约70.8%，但较双排钻孔并无显著提升。即可得知当钻孔排数为一定值时钻孔卸压对于降低能量释放速率及能量耗散速率会有显著效果，从而能够起到防治冲击地压的作用。

图17 峰后能量释放、耗散速率Fig.17 Energy release and dissipation rate after peak

4 结 论

(1)钻孔使试样以剪切劈裂破坏转变为在孔洞两侧孕育、融合裂隙形成贯穿裂纹的破坏形式，并伴随塌孔现象。较完整试样，钻孔试样随钻孔排数增多，其单轴抗压强度、冲击能量指数、弹性能量指数均逐渐降低，动态破坏时间逐渐升高，表现随钻孔排数增多，钻孔试样的冲击倾向性逐渐降低。

(2)破碎颗粒分形维数D与新增表面积ΔSa具有良好的负相关性:试样破碎程度越低，分形维数越高，新增表面积越小。新增表面积与能量耗散呈正相关性，且峰后能量差值与新增表面积呈“U”形变化规律是受单轴加载速率、钻孔垂直布置影响。

(3)降低应力峰前储存弹性应变能Uet1、峰后能量ΔU和提升耗散能量ΔUd对防止煤岩体发生动力破坏均具有重要作用。较完整试样，钻孔试样随钻孔排数增多，其峰前弹性应变能密度Uet1逐渐降低，峰后耗能ΔUd与新增表面积ΔSa均先降低后升高，且二者呈正相关性。表明钻孔卸压不仅可以降低峰前积聚的弹性应变能，还能提升峰后破碎耗散的能量，从而降低引发动力破坏的可能性。

(4)钻孔增多使得应力峰后阶段的能量释放、耗散速率逐渐减缓，单孔试样降低约 17.0%，双孔试样降低约68.3%，三孔试样降低约 70.8%。单位时间内释放的能量降低，会降低动力破坏的剧烈程度。综上可知钻孔卸压可以有效地作用于降低应力峰前积聚的能量、减缓峰后能量的释放，从而起到防治冲击地压的作用。