动车组车轮多边形磨耗形成与发展过程仿真研究

胡晓依，任海星，成 棣，侯茂锐，孙丽霞

（1.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081；2.北京交通大学 机械与电子控制工程学院，北京 100044）

车轮多边形磨耗即车轮半径沿着车轮整个圆周呈周期性或非周期性的变化，广泛存在于轨道车辆中[1-2]。2014年以来，我国部分高铁线路上运行的动车组出现明显高阶车轮多边形磨耗。一方面，车轮多边形磨耗会造成轮轨系统振动响应明显增大，降低动车组运行品质，导致部分动车组轴箱温度传感器电缆线卡支座裂纹等问题，车轮多边形磨耗严重时还可能导致轴端螺栓松脱、折断以及钢轨扣件弹条断裂，危及行车安全。另一方面，车轮多边形磨耗会使得车轮镟修里程缩短，车轮寿命减少，从而增加高速铁路养护维修成本[3]。因此，当前开展动车组车轮多边形磨耗相关问题研究，对于延长车轮使用寿命，降低高速铁路养护维修成本、提升动车组运行安全可靠性具有重要意义。

对于动车组车轮多边形磨耗的成因，目前业界还未达成共识。一些学者认为其主要是由转向架共振导致，在某特定速度条件下，共振的波长能够整分车轮的周长时车轮多边形磨耗进入高发期[4]。另有一些学者则认为是由轨道部件的共振、车辆与轨道的动力学相互作用导致了车轮多边形磨耗[5-6]。以上观点均未得到完整的仿真和试验数据证实，仍存在较大的争议和质疑，对该问题的研究有待进一步深入。弄清车轮多边形磨耗形成和发展机理，明确车轮多边形磨耗形成和发展的主要影响因素，应是当前车轮多边形磨耗问题研究的重点。

在车轮多边形问题仿真研究方面，Johansson[7]和Zobory[8]对车轮和钢轨磨耗问题进行全面的研究，对车轮磨耗预测的数值方法进行文献综述，总结出长期磨耗迭代模型。Morys 等[9]建立ICE-1型高速列车动力学模型，将车轮和制动盘视为刚体，为表征轮对的弯曲和扭转特性，采用三维旋转弹簧-阻尼单元连接各刚体，研究车轮多边形磨耗的成因和发展规律。Meywerk 等[10]为研究车轮多边形的形成过程，建立单个柔性轮对在弹性轨道上运行的动力学模型，同时考虑车轮材料硬化对磨损率的影响。Johansson 等根据FASTSIM算法，基于滚动接触力学理论建立三维瞬时轮轨动力学模型，其中轮对模型由刚性车轮和柔性车轴组成，轨道模型中钢轨采用离散支承的Timoshenko梁单元，以实测车轮初始多边形作为输入，使仿真结果更接近实际情况。Wu 等[11-12]研究发现钢轨3阶弯曲振动对轮轨力的周期性波动具有重要影响，认为其是导致我国高速动车组车轮多边形磨耗产生的主要因素。

通过仿真手段研究车轮多边形磨耗成因问题的关键和主要难点之一，在于如何真实地模拟车轮多边形磨耗的整个发展过程。如能突破这一难点，就可定量分析车轮的多边形化过程，并清楚地揭示其发生机理。由于动车组车轮高阶多边形的激励频率已覆盖到轮对、钢轨弹性振动的范围，采用传统的基于多刚体的车辆动力学模型无法考虑轮对、钢轨弹性振动对轮轨接触行为和车轮磨耗的影响，难以满足车轮多边形磨耗问题仿真要求。

本文通过建立基于柔性钢轨和柔性轮对的车辆-轨道耦合动力学模型[13-14]，分析轮对、钢轨弹性振动对轮轨接触行为和车轮磨耗的影响；使用Hertz接触理论以及FASTSIM算法[15-16]得到接触区域内的压应力、切应力等参数，结合Archard 磨耗模型构建车轮多边形磨耗的长期磨损迭代模型，研究我国高速动车组车轮多边形磨耗的成因及影响其发展的主要因素。

1 车轮多边形磨耗数值模拟

1.1 长期磨损迭代模型

构建车轮多边形磨耗长期磨损迭代模型基于3个假设。第1个假设，车轮和钢轨的材料属性和型面在短时间内是恒定的，因此在1次短期计算中轮轨型面的变化可以忽略不计。第2个假设，称为多个时间尺度假设，将尺度系数用于短期动态模拟，其结果可用于模拟在更长的时间尺度上发生的磨耗效果。第3个假设，是在计算过程中车轮踏面型面不会发生改变。

长期磨损迭代模型主要由以下4个部分组成。

（1）车辆-轨道耦合动力学模型：输入初始车轮多边形数据，设置合适的采样频率，计算得出车辆稳定运行时各个接触斑的大小、法向力、蠕滑率、kalker系数等参数。

（2）轮轨接触模型：利用车辆-轨道耦合动力学模型计算得出的上述参数，结合FASTSIM算法和库伦摩擦定律计算接触斑内黏着区和蠕滑区的法向力分布，以及蠕滑区内的滑动量分布。

（3）车轮磨耗模型：利用轮轨接触模型计算得出的数据，结合Archard 磨耗模型计算得到接触斑内的车轮磨耗量分布，将车轮磨耗量进行纵向叠加，选取平均值作为该采样点在车轮旋转1 周产生的磨耗量，使用傅里叶级数对滚动圆上的磨耗量进行拟合，用以表示车轮整个滚动圆上的磨耗量分布。

（4）循环迭代模型：在初始车轮多边形的基础上，减去车轮磨耗模型计算出的车轮滚动圆磨耗，得出新的车轮多边形，并将其代入到新一轮的计算当中。

1.2 车辆-轨道耦合动力学模型

以某型高速动车组为研究对象，根据多体动力学理论，结合该型高速动车组的结构和悬挂参数，在多体动力学软件SIMPACK 中建立包括1个车体、2个构架、4个轮对、8个轴箱共50个自由度的多刚体动力学模型，其中车体、构架、轮对均考虑横向、垂向、纵向、点头、摇头和侧滚6个方向的自由度、轴箱只考虑其相对轮对点头方向的自由度[17]。

该型高速动车组车轮型面为LMB型，车轮初始直径为920 mm。先利用CAD软件建立该型车轮的三维模型，在该模型中将2个车轮和1个车轴考虑为1个整体，不考虑车轮与车轴的过盈配合关系，忽略车轴过渡圆弧和倒角等。再在Hypermesh软件中对轮对进行网格划分，整个轮对采用六面体网格进行划分，单元属性为3D 实体单元solid45。然后在车轴轴肩、车轴与轴箱的铰接位置以及车轮滚动圆等处选择主自由度点，使用有限元分析软件ANSYS 对轮对进行模态缩减计算，如图1所示。最后通过多体动力学软件SIMPACK 中的FLXBODY模块，将原有的刚性轮对替换成柔性轮对。

在SIMPACK 软件中建立柔性轨道时，不仅需要建立钢轨（型号为TB60）的3D 有限元模型，还需要编写柔性轨道的配置文件，通过SIMPACK软件中的FLEXTRACK 模块读取配置文件，从而将柔性轨道导入。其中，轨枕间距为0.63 m，钢轨的密度为7 850 kg·m-3，弹性模量为210 GPa，泊松比为0.3。轨道端部利用力元进行固定，横向、垂向和纵向3个方向的刚度均为104MN·m-1，阻尼为104kN·s·m-1。扣件、轨枕、道床等轨下部分统一采用弹簧阻尼元件模拟，垂向刚度为20 MN·m-1，垂向阻尼为30 kN·s·m-1。

1.3 车轮磨耗模型

轮轨接触模型是联系车辆和轨道子系统中的重要纽带。现场测试表明，我国动车组车轮多边形磨耗的波长范围为100～150 mm，约为轮轨接触斑纵向轴长的10倍，因此仍然可以使用Hertz接触理论计算接触斑内的压应力分布，再结合FASTSIM算法和Archard 磨耗模型就可得出接触斑内的磨耗分布情况。

图1 轮对柔性化建模

通常认为在FASTSIM算法中将接触区域划分为（10×10）个单元，就可以比较合理地区分出黏着区和蠕滑区以及法向力在接触区域的分布情况[18]。而Johansson的研究表明，预测精度随单元格划分数量的增加而增加，密集的离散化可以提供连续的磨耗分布[19]。因此，将接触区域划分为100×100个单元，单元的纵向、横向长度分别为Δx和Δy。

在众多计算磨耗的模型中，Archard 磨耗模型因为其较快的计算速度和较好的计算精度被广泛采用，Archard磨耗模型的定义为

式中：Vwear为磨耗材料体积；Kw为磨耗系数；FN为法向接触力；d为滑动距离；H为轮轨接触时较软材料的硬度。

在研究时仅模拟了直线轨道，轮轨之间滑动量相对较小，因此假设磨耗系数为10-4，车轮表面硬度为3 GPa[20]。对于接触区域某一中心坐标为（x，y）的离散单元，其磨耗Δz可以根据Archard磨耗模型得出，即

式中：a，b分别为接触斑的纵向、横向半轴长；ξ1，ξ2，ξ3分别为纵向、横向以及自旋蠕滑率；τx，τy分别为纵向和横向的切应力；C11为轮轨纵向蠕滑系数；C22为轮轨横向蠕滑系数；G为车轮材料的剪切模量。

因在仿真中仅考虑直线轨道，则轮轨间的相对滑动较小，车轮的横向位移很小，可假定接触斑的中心位置始终位于车轮滚动圆上。为保证计算精度和计算速度，仅研究车轮滚动圆上不同位置处的磨耗情况。仿真研究时，将车轮滚动圆离散为3 600个采样点。对计算出的接触斑内各采样点车轮磨耗进行纵向叠加，并选取其平均值作为该采样点在滚动圆上的磨耗，即

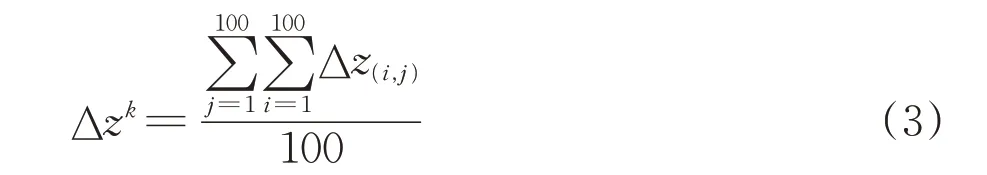
式中：Δzk为滚动圆上第k个离散点的磨耗；Δz(i，j)为接触斑内上纵向第i，横向第j个网格的磨耗。

计算出车轮旋转1 周离散点的磨耗后，使用傅里叶级数对整个滚动圆上的磨耗情况进行拟合，得

式中：z0为拟合后的磨耗量；a0为车轮旋转1 周磨耗的平均值；at和bt分别为第t阶傅里叶级数的正弦和余弦函数的系数；一般来说有意义的车轮多边形阶次不超过30阶，因此最大阶次n取40 即可满足拟合准确性的要求。

2 车轮多边形发展过程

假设车辆在较短运行距离内的车轮磨耗累积量与行驶距离呈线性增长，则可以将车轮旋转1周产生的磨耗乘以1个尺度系数表示车轮在运行一段距离后的磨耗累积量，将这个磨耗累积量与初始多边形相结合即得到车辆运行一段距离后的车轮多边形。假设磨耗累积量随运行距离的增加呈分段线性增加，因此不断重复上述过程就可以获取车辆长距离运行下车轮多边形的发展过程。

仅考虑直线轨道，车速设置为300 km·h-1，忽略轨道不平顺的影响，以实测初始车轮多边形作为输入，当车辆稳定运行时提取车轮旋转1 周的动力学计算结果，提取轮轨接触区域的轮轨力、接触斑大小、蠕滑率等参数，计算得到车轮旋转1 周的磨耗情况。尺度系数取2×105时，车轮旋转1 周的磨耗就可以表示车轮运行578 km的磨耗累积量。

仿真研究1个镟修周期内车轮多边形磨耗发展的演变过程时，迭代次数设置为60次，若出现跳轨现象则停止迭代。1位轮对左右车轮周向磨耗累积深度发展演变过程的极坐标如图2所示，对应的以阶次谱形式表示如图3所示。

图2 车轮周向磨耗累积量发展演变过程（极坐标）

由图2和图3可知：使用长期磨损迭代模型经过60次迭代后，车轮滚动圆由最初的无明显高阶多边形，发展到最后20阶占据主导；这一现象与该动车组实际运行产生车轮多边形的阶次特征一致，验证了长期磨损迭代模型的正确性。

图3 车轮多边形发展演变过程（阶次谱）

3 车轮多边形产生原因

车轮多边形磨耗的形成和发展是一个复杂而长期的过程，影响因素非常多，现场试验和实验室试验均存在较大的局限性，无法对这些影响因素进行一一识别。采用长期磨损迭代模型模拟车辆以300 km·h-1速度运行一段距离车轮多边形的发展情况，结果与实际情况相吻合。因此，可采用该模型深入研究车辆运行速度、轮轨模态振动特性及轨道参数等因素对车轮多边形发展过程的影响，进而找出导致车轮多边形产生的原因。

3.1 车辆运行速度的影响

如前文所述，对于车轮多边形磨耗，学术界还没有给出被普遍认可的完整清晰的产生机理。目前，用“频率固定”机理解释动车组车轮多边形磨耗的发生发展机理的认可度较高。在我国，动车组的运行速度一般在200～350 km·h-1之间，因此下文使用长期磨损迭代模型研究动车组运行速度v分别为200，250，300 和350 km·h-1时车轮的磨耗情况，结果如图4所示。由图4可知：车轮多边形主导阶数分别为30，24，20和17阶。

图4 不同速度等级下车轮磨耗情况

车轮多边形阶数与激励频率的关系为

式中：f为车轮多边形产生的激励频率；n为车轮多边形的阶数；r为名义滚动圆半径。

根据图4和式（5）发现，这些车轮多边形导致的激励频率分别为576，577，577 和572 Hz，均在550～600 Hz 之间，仿真结果进一步验证了“频率固定”机理。尽管车辆在实际运行过程中受到的外部激励（例如车轮表面损伤、轨道不平顺等）是随机且不可控的，然而运行一段时期之后车轮产生的周期性磨耗遵循“频率固定”机理，因此可以认定车辆在运行过程中轮对与钢轨之间存在1个固定频率的振动激扰，该频率应是某一结构模态频率，存在于钢轨与轮对的二者其一或同时存在。

3.2 轮轨模态振动特性的影响

由前文分析可知，车辆在运行时轮对与钢轨之间存在1个固定频率的振动激扰，这个振动频率在550～600 Hz 之间，与车轮多边形磨耗导致的激扰频率吻合。因此，可以认为正是由于这个固定频率的存在导致车轮多边形的产生。前文证实了“频率固定”现象，但对固定频率的来源还需进一步研究。长期磨损迭代模型使用刚柔耦合动力学模型，结合Archard 磨损模型，仿真出车轮多边形的产生、发展的全过程。由于建立的车辆-轨道耦合动力学模型中同时考虑轮对和钢轨的柔性，保留轮对和钢轨的模态振动特性，该模型能够研究钢轨和轮对模态特征对车轮多边形磨耗仿真结果的影响。下文分别研究柔性轮轨、刚性轮柔性轨、柔性轮刚性轨、刚性轮轨这4种工况下车轮多边形磨耗的发展演化过程。车辆运行速度为300 km·h-1，以阶次图表示的车轮多边形发展演变过程如图5所示。

由图5可知：当钢轨为柔性时，轮对无论是被考虑成柔性还是刚性，车轮多边形最终均演化成以20阶占主导；当考虑钢轨为刚性时，轮对无论是被考虑成柔性还是刚性，车轮多边形最终均未演化成以20阶为主导；当采用柔性轮刚性轨进行计算时，车轮多边形最终演化成以3阶占主导；当采用刚性轮轨进行计算时，车轮多边形最终演化成以8阶占主导。以上仿真结果表明，钢轨的模态振动特性对车轮多边形发展演变具有较大的促进作用，而车轮的模态振动特性对车轮多边形发展演变的促进作用相对较小。

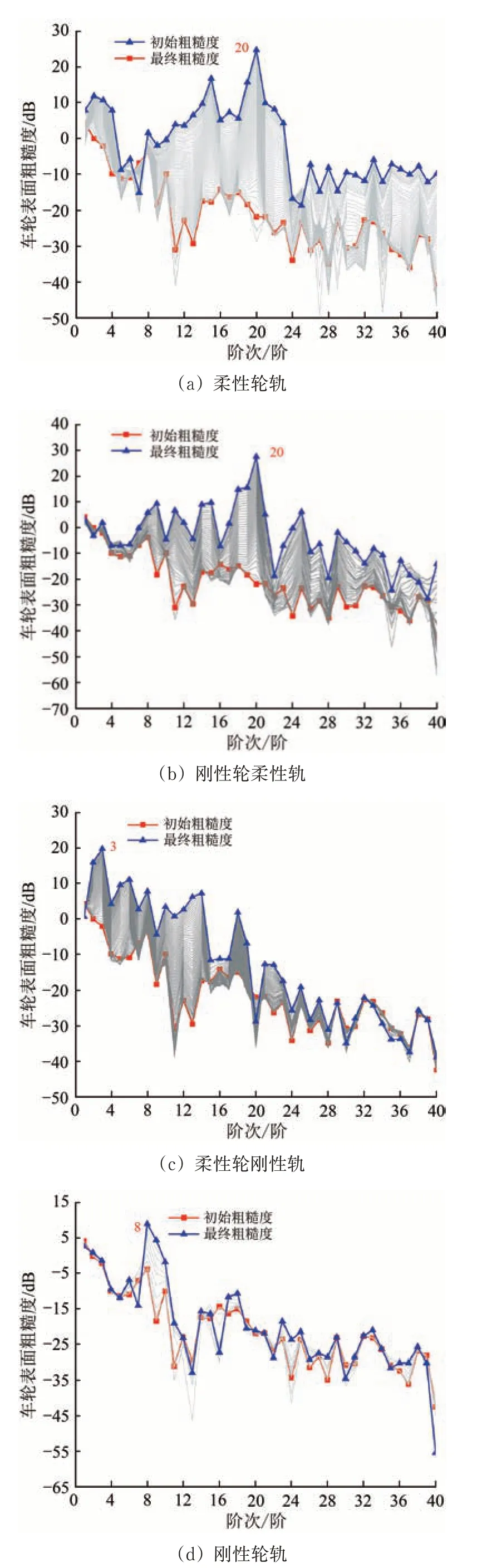
图5 4种工况下车轮多边形发展演变过程

3.3 轨道参数的影响

通过上述研究已经得知，钢轨的模态振动特性对车轮多边形的产生与发展具有较大的促进作用，而2个轮对间钢轨的局部弯曲模态与扣件的刚度阻尼特性相关，因此扣件刚度、阻尼的变化可能将影响钢轨的振动状态，进而影响车轮多边形的发展。扣件垂向刚度分别取20，40，80，120 MN·m-1，和扣件垂向阻尼取30 kN·s·m-1时采用长期磨损迭代模型计算得出车轮多边形磨耗的发展演化情况如图6所示。

由图6可知：当扣件垂向刚度小于80 MN·m-1时，随着刚度的增大，低阶（2阶和3阶）车轮多边形所占比例逐渐增高，但此时20阶车轮多边形仍然占据主导，车轮表面粗糙度水平在20 dB以上；当扣件刚度达到80 MN·m-1时，2阶车轮多边形占据主导，此时20阶多边形的粗糙度水平在15 dB 左右；随着扣件刚度的进一步增大至120 MN·m-1时，3阶多边形占据主导地位，此时20阶车轮多边形的粗糙度水平降至10 dB以下。产生这种现象是由于扣件垂向刚度过大，抑制了钢轨的高频振动，从而导致车轮多边形由高阶转变为低阶。

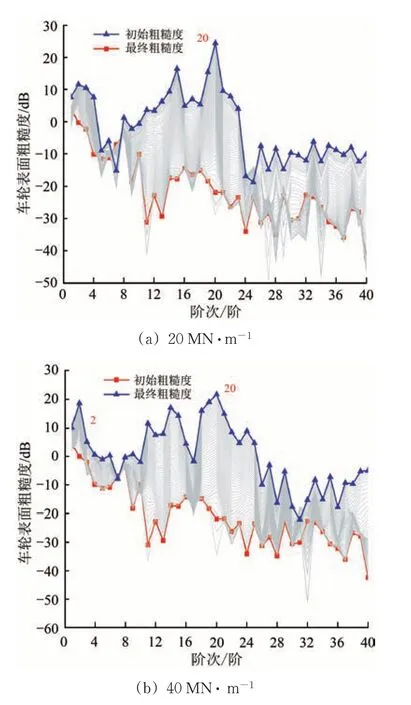
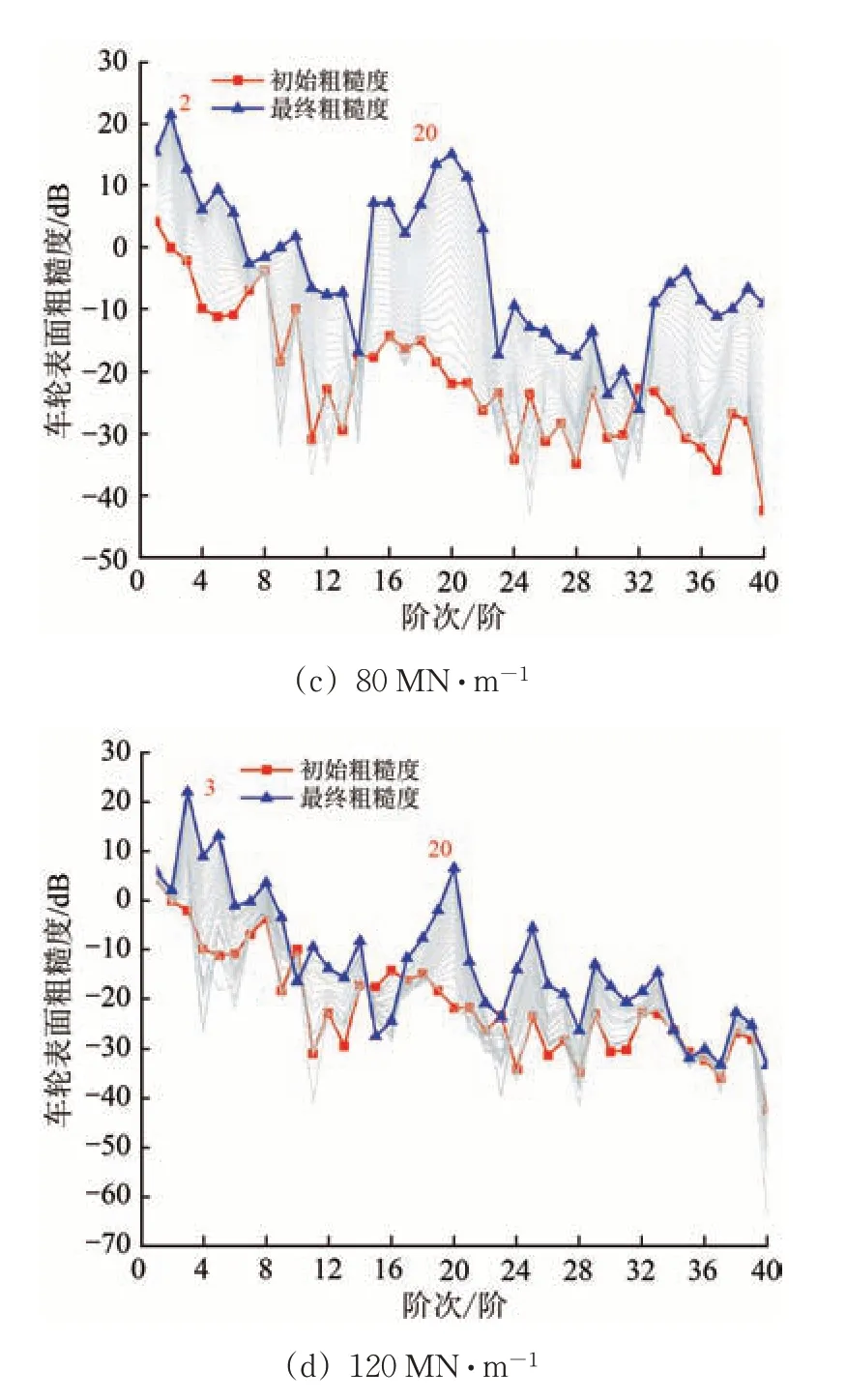
图6 扣件刚度对车轮多边形发展过程的影响

扣件垂向刚度均取20 MN·m-1，扣件垂向阻尼分别取30，60和100 kN·s·m-1对车轮多边形发展的影响由图7所示。由图7可知：当扣件阻尼从30 kN·s·m-1增大至60 kN·s·m-1时，高阶车轮多边形的表面粗糙度由25 dB降至0 dB以下，但仍然存在较大的低阶多边形，其中1～3阶车轮表面粗糙度均在20 dB以上；随着阻尼继续增大至100 kN·s·m-1，车轮已不存在明显多边形现象，最大车轮表面粗糙度约为10 dB，由此可见，增大扣件阻尼可抑制车轮多边形的发展速度。

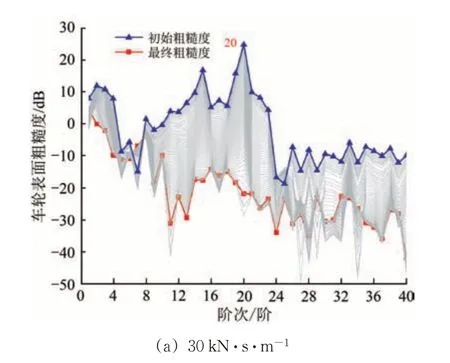
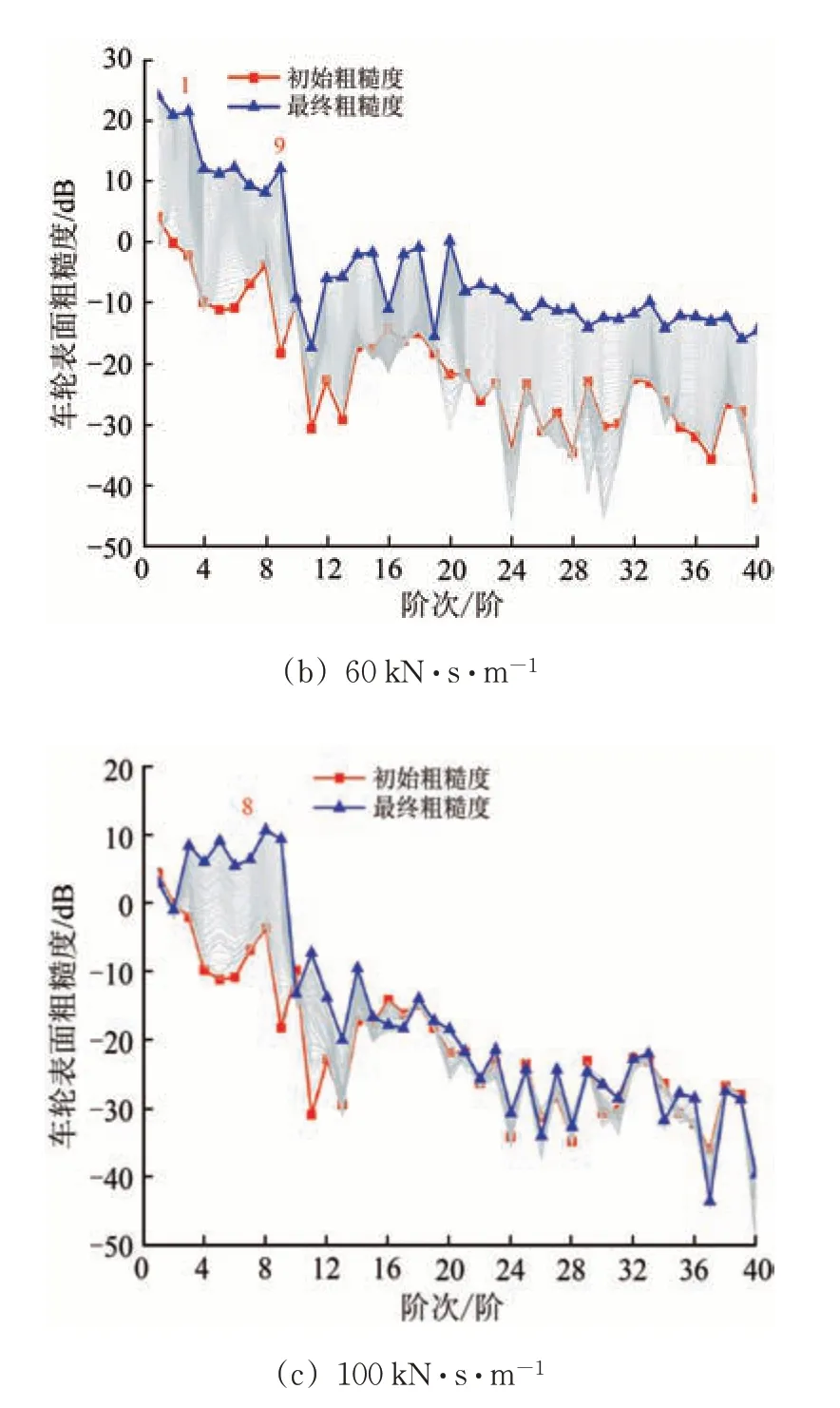
图7 扣件阻尼对车轮多边形发展过程的影响

4 结 论

（1）使用长期磨损迭代模型模拟我国某型高速动车组以300 km·m-1速度长距离运行后车轮多边形的发展情况，结果与实际情况吻合，验证了长期磨损迭代模型的准确性。

（2）研究动车组运行速度分别为200，250，300 和350 km·m-1时车轮多边形的发展过程，结果显示车轮多边形激励频率均在550～600 Hz 之间，符合“频率固定”机理，进一步验证了长期磨损迭代模型的准确性。

（3）通过对比分析柔性轮轨、刚性轮柔性轨、柔性轮刚性轨、刚性轮轨4种工况下车轮多边形的发展过程，发现轮对的模态振动特性对高阶车轮多边形成的促进作用很小，而钢轨的模态振动特性对于高阶车轮多边形的产生有一定的促进作用。

（4）增大扣件刚度可以使车轮多边形由高阶转变为低阶，增大扣件阻尼可以抑制车轮多边形的发展速度。