基于强迫振动的列车-轨道-轨下结构垂向耦合动力分析方法及工程应用

（中国铁道科学研究院集团有限公司 基础设施检测研究所，北京100081）

我国高速铁路开通已逾十年，在大运量、高速度以及长期运营条件下，基础设施服役状态已与建成初期有所不同，桥梁徐变上拱[1-2]引起轨道状态劣化，轨道板温度变形[3]导致轨道板与砂浆层出现离缝[4-5]、沉降[6]持续发展超出规范限值、大跨度桥梁温度变形[7]显著、梁端伸缩装置工作状态不良等现象相继出现，病害机理分析、动力性能评估以及评价标准制定的需求日益迫切，传统的列车-轨道-桥梁动力分析模型更侧重于设计阶段的动力性能评估，对局部轨道或轨下结构的参数变化难以准确模拟。因此，需要针对线路结构提出更为精细化和高效率的动力分析模型，同时也需要对列车-线路-桥梁的动力分析算法作出相应的改变。

线路动力分析模型中，钢轨是连接车辆与线路的纽带，对钢轨的处理直接影响计算效率和精度，本文在分析传统线路模型及其局限性的基础上，提出优化的线路结构处理方案和列车-线路-轨下结构的动力分析方法，将路基、桥梁、隧道等基础设施统一处理为轨下结构，不仅能够实现对局部病害的准确模拟，也简化了不同类型基础设施组合结构的动力分析。

1 传统线路结构模型及其局限性

较早的车桥振动研究工作大都以桥梁为主体，未考虑（或简单考虑）轨道结构参振影响，常常是将整个钢轨-轨枕-道床质量体系作为二期恒载加到梁体上，以梁体位移和轨道随机不平顺之和作为钢轨位移计算轮轨作用，随着各种无砟轨道结构的广泛采用，轨道与桥面之间的随动性明显受到轨道结构的影响，轨道结构参振就成为不应忽视的因素。

陈松、雷晓燕、朱志辉等[8-9]采用有限元法建立钢轨-桥梁整体模型，通过直接刚度法求解钢轨和桥梁的动力响应。由于桥梁和线路在材质、质量、刚度上存在明显差异，在单元尺寸、线路布置上需要互相协调，因此建模难度较线、桥分离模型大，且线桥一体会导致结构的求解规模显著增长，也在一定程度上影响了计算效率。

目前更为普遍的是线-桥分离模型，以板式无砟轨道为例说明，图1为典型的板式轨道动力学模型侧视图（为方便说明，未画出桥梁结构）。图中：Er为钢轨材料弹性模量；Jr为钢轨截面抗弯惯性矩；ρr为钢轨材料容重；kpv和cpv分别为轨下胶垫的刚度和阻尼；ksv和csv分别为CA砂浆的刚度和阻尼。

图1 板式轨道动力学模型

板式轨道由钢轨、扣件、轨道板、凸形挡台、CA砂浆及混凝土底座等组成，轨道的振动主要体现在钢轨和轨道板的振动上，钢轨与轨道板以及轨道板与混凝土底座之间分别由轨下胶垫和CA砂浆提供弹性，左右2 股钢轨均视为离散弹性点支承基础上的无限长Euler 梁，在考虑钢轨振动的边界条件影响后，翟婉明[10]、高芒芒[11]、张健[12]等人将线路模型中的钢轨与轨下结构分别考虑，钢轨的无限长Euler 梁模型简化为有限长简支梁模型，引入钢轨的正则坐标，采用振型叠加法[13-14]建立钢轨运动方程，列车荷载以及轨下胶垫的支承均为简支梁所受的外荷载，此时钢轨的力学模型及受荷状态如图2所示。图中：x0为车辆最后1个轮对距钢轨端部的距离；l为车辆定距之半；l1为车辆轴距之半；Fp1，Fp2，Fp3和Fp4为车辆作用于钢轨的轮轨垂向力；Frs1，Frs2，Frsi和Frsn为轨下结构作用于钢轨的垂向力；zr为钢轨垂向位移；L为钢轨计算长度；xi（i=1，2，…，n）为各扣件x坐标；v为列车速度。

图2 传统线桥结构中钢轨受力

尽管实际振动过程中钢轨在扣件位置处所受的支承力随荷载增加而同步增大，但在动力分析过程中需要确定性荷载才能进行位移计算，因此实际的计算流程如下。

（1）计算轮轨垂向力作用下的钢轨位移；

（2）根据计算出的钢轨位移，计算各扣件位置处的支承反力；

（3）计算支承反力与轮轨力共同作用下的钢轨位移；

（4）如果此时钢轨位移与计算轮轨力时采用的钢轨位移之差超过允许误差，则重新计算轮轨力；

（5）重复上述步骤（1）—步骤（4），直至前后2次计算的钢轨位移差满足迭代精度。

上述钢轨的动力分析模型计算精度显然受到计算长度的影响，当计算长度较长时，将钢轨处理成简支梁会造成钢轨位移的反复动荡，通过理论推演，如不考虑惯性力和阻尼力的影响，只考虑静力情况，则计算结果的收敛性要求由轨下胶垫提供的支承刚度不大于钢轨作为简支梁提供的刚度值的2倍，尽管引入正则坐标后通过限制截止模态的阶数可以解决这一矛盾，但限制模态阶数同时也导致钢轨的局部高频振动无从反映[15]，因而计算得到的钢轨动力分析结果较实际情况偏小。

2 优化后线路结构模型及其特点

为实现对局部轨道病害的模拟，同时避免将钢轨处理为简支梁后可能产生的计算发散，需要建立钢轨子系统和轨下结构子系统的三维有限元模型，并采用直接刚度法计算动力响应，但同时为降低建模难度和减小求解规模，又需要将线-桥结构适当分离。图3为优化后轨道系统和轨下结构垂向耦合动力学模型。

图3 轨道系统和轨下结构垂向耦合动力学模型

用弹簧-阻尼单元模拟轨下胶垫，将由钢轨和扣件组成的钢轨子系统和由轨道板、桥梁、隧道等组成的轨下结构子系统分别处理，列车荷载仍为钢轨子系统的外荷载，但轨道板对钢轨子系统的作用则以扣件处强迫位移和强迫速度的形式施加给钢轨子系统，这样可以更好地体现出钢轨和轨下结构各自的振动情况，消除了采用力的边界条件模拟轨下胶垫对钢轨的约束引起的不收敛的可能性，且轨下结构与钢轨子系统的建模各自独立，可较为方便地适应多种轨道形式及特殊工况，如轨道板脱空，扣件失效、过渡段、桥梁、隧道等。此时钢轨的力学模型及受荷状态如图4所示。图中：zsi，vsi分别为轨道板各扣件位置处的垂向位移和垂向速度。

图4 优化后线桥结构中的钢轨受力

3 车辆、钢轨系统、轨下结构模型及其运动方程

采用优化后的线路结构时，车辆-轨道-轨下耦合系统包括3个子系统：车辆子系统、钢轨子系统和轨下结构子系统。基于多刚体理论建立车辆模型，基于有限元建立钢轨子系统和轨下结构子系统模型，其中轨下结构对钢轨子系统的作用以扣件处强迫位移和强迫速度的形式施加，而钢轨子系统对轨下结构的作用则以荷载的形式表现，各子系统均采用直接刚度法求解动力响应。

3.1 车辆模型及运动方程

列车含有多节车辆，每节车辆包含1个车体、2个转向架和4个轮对。以二系悬挂客车为例，考虑列车的垂向振动，每节车包括车体、构架的沉浮和点头以及轮对的沉浮共10个独立自由度。车辆动力分析模型如图5所示，其中各变量对应的物理意义见表1。

图5 车辆动力分析模型

表1 车辆模型中各变量的物理意义

假定车辆的位移向量为Xv，速度向量为加速度向量为根据多刚体理论和D’Alembert原理，形成车辆运动方程，即

式中：Mv，Cv和Kv分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵；FV为振动过程中作用于车辆各自由度的荷载向量。

车辆的质量、阻尼和刚度阵构成如下。

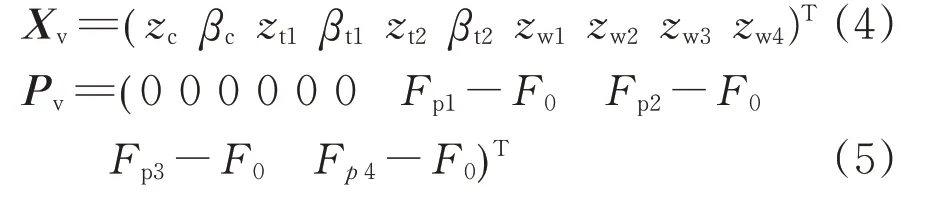
式中：F0是轮对的平均静轴重。

阻尼矩阵Cv与刚度矩阵Kv形式类似，不再赘述。

3.2 钢轨和轨下结构动力分析模型及运动方程

如图3所示，采用上下对应的2层节点建立钢轨子系统模型，钢轨为具有弹性离散点支承的连续Euler梁，下层节点表征扣件，上下节点间用弹簧-阻尼单元表述轨下胶垫的弹性约束。

假定钢轨子系统的位移向量为Xr，速度向量为，加速度向量为由钢轨刚度矩阵、质量矩阵及荷载向量可得出钢轨的动力平衡方程如下。

式中：Mr，Cr和Kr分别为钢轨的质量矩阵、阻尼矩阵和刚度矩阵；Fr为振动过程中作用于钢轨各自由度的荷载向量。

轨下结构模型可采用板单元、梁单元、弹簧-阻尼单元等形式模拟包括有砟或无砟轨道、路基、桥梁和隧道等结构。

假定轨下结构的位移向量为Xb，速度向量为加速度向量为则轨下结构运动方程可写成矩阵形式，即

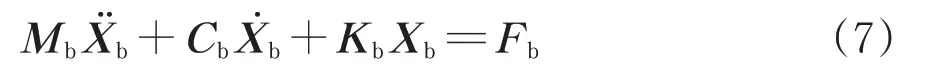
式中：Mb，Cb和Kb分别为轨下结构的质量矩阵、阻尼矩阵和刚度矩阵；Fb为轨下结构的广义荷载向量。

3.3 车辆-轨道-轨下结构耦合方程及分析方法

分别建立了车辆、钢轨和轨下结构的动力平衡方程后，完整的列车-轨道-轨下结构就被分解为3个子系统、2个作用界面的耦合系统，其中列车与钢轨间的相互作用体现为轮轨力，钢轨与轨下结构间的相互作用则体现为轨道板以扣件处强迫位移和强迫速度作用于钢轨，同时钢轨以扣件位置处的弹簧力和阻尼力反作用于轨道板，3个子系统间通过力的平衡条件和变形协调条件进行耦合。耦合系统的运动方程可表示为

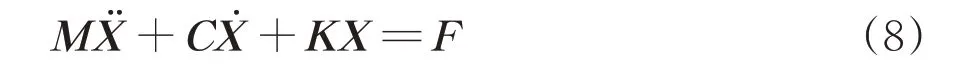
其中，

式中：X，分别为耦合系统的位移、速度、加速度及荷载列向量；M，C和K分别为耦合系统的质量矩阵、阻尼矩阵和刚度矩阵。

在确定轮轨力时，采用Hertz 非线性弹性接触理论，允许轮轨脱离，即发生跳轨，计算轮轨力时考虑轨道几何不平顺的影响。

在计算轨下结构对钢轨子系统的作用时，扣件处的强迫振动采用常见的“主1 赋0 法”[16]对钢轨系统的刚度矩阵和阻尼矩阵进行处理，由于轨下胶垫在模型中视为无质量的弹簧-阻尼单元，因此不考虑轨下结构振动加速度对钢轨子系统的影响；在计算钢轨子系统对轨下结构的作用时，则依据钢轨与轨道板间的相对位移和相对速度直接计算。

确定列车、轨道和轨下结构的动力方程后，采用Newmark-β方法进行求解。由于每时间步各子系统之间的相互作用均与该时刻的系统响应有关，因此需要反复迭代。在计算各子系统间的相互作用时已经采用了力的平衡条件，因此以车辆、钢轨与轨下结构在每时间步的相邻2次迭代间的位移差满足精度要求作为收敛条件，选取的位移精度限值为0.1 μm。计算流程如图6所示。

图6 动力分析流程

4 模型验证

为了验证方法的正确性和实用性，建立路基+10跨32 m 简支梁桥+路基的线桥结构模型，铺设无砟轨道，10跨32 m 简支梁桥和桥上轨道有限元模型分别如图7和图8所示。为充分考虑线路随机不平顺和桥梁徐变上拱的影响，选取图9所示实测轨道静态高程数据作为输入不平顺。可见，桥梁徐变上拱引起的轨道高低峰峰值最大可达5.02 mm。车型为中国高速综合检测列车CRH380A型车，行驶速度为300 km·h-1，考虑进、出桥和车辆自身长度的影响，线桥模型总长度为1 000 m。进行车辆-轨道-桥梁动力仿真分析。

图7 10跨32 m简支梁桥有限元模型

图8 桥上轨道有限元模型

图9 实测轨道静态高程数据

图10给出了车体垂向振动加速度的实测及仿真分析结果。实测车体垂向振动加速度最大值为0.540 m·s-2，计算值为0.566 m·s-2。实测值与计算值吻合良好。

图10 车体垂向振动加速度

图11给出了仿真分析得到的路基段和桥梁跨中的垂向位移时程曲线。由图11可见：路基段和桥梁跨中钢轨、桥梁的最大垂向位移分别为0.825，1.248 和0.440 mm，计算结果与中国某高速铁路联调联试实测结果基本吻合。

图11 钢轨和桥梁垂向位移

通过分析结果与实测数据的对比分析，可确认本文模型能够充分反映车辆、线路和桥梁的振动响应，计算精度达到工程应用的要求。

5 应 用

本文所建立的车辆-轨道-轨下结构动力分析模型可以考虑线路、桥梁等基础设施局部病害对系统动力响应的影响，以扣件失效为例，分析长100 m的CRTS I型板式无砟轨道线路，考虑到边界效应、列车长度和运行稳定性等问题，无砟轨道总长为700 m，如图12所示。

图12 无砟轨道局部有限元模型

参考现场调研结果，选取线路中部352.836 和353.465 m处连续2个扣件失效的病害工况，详见图13，进行扣件失效与扣件正常服役条件下，车辆、钢轨、轨道板动力响应对比仿真分析。

扣件失效可以采用2种方法进行模拟，一种是将对应扣件提供的刚度和阻尼赋值为0，另一种是取消强迫振动传递，即不考虑此位置轨下结构与钢轨之间的相互作用，本文采用后一种。模型中轨下弹性垫层垂向静刚度为25 MN·m-1，阻尼为70 kN·s·m-1。列车编组为4 动4 拖，计算车速分别为300，320，340，350 和385 km·h-1，选取的不平顺如图14所示。

图13 扣件失效位置图

图14 高速铁路路基段轨道几何不平顺

表2给出了扣件失效以及扣件正常服役情况下车辆及352.836 和353.465 m处钢轨、轨道板的动力响应最大值，图15—图19给出了在350 km·h-1速度条件下，352.836 和353.465 m处的钢轨位移和振动加速度、轮对振动加速度及轮轨力时程曲线。

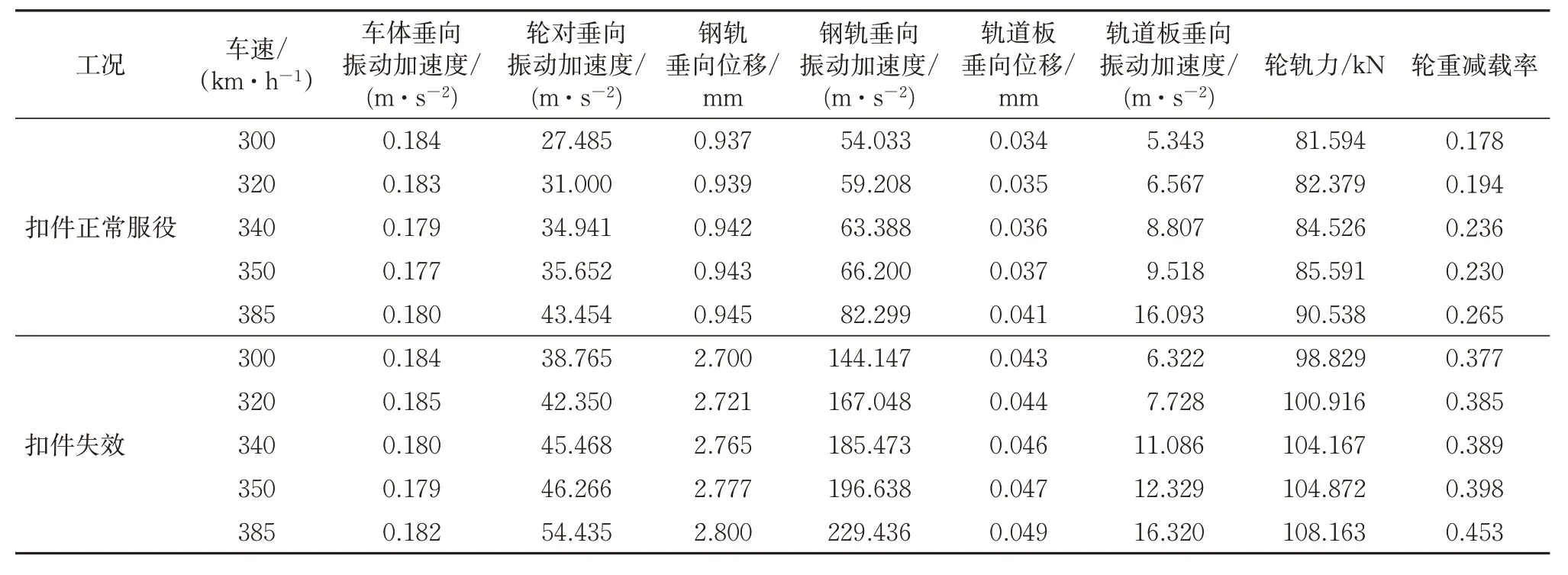
表2 车辆、轨道动力响应最大值

图15 350 km·h-1车速时扣件失效和正常服役情况下钢轨垂向位移时程

图16 350 km·h-1车速时扣件失效和正常服役情况下不同扣件位置处钢轨垂向位移

图17 350 km·h-1车速时扣件失效和正常服役情况下轮对垂向振动加速度时程

图18 350 km·h-1车速时扣件失效和正常服役情况下钢轨垂向振动加速度时程

图19 350 km·h-1车速时扣件失效和正常服役情况下轮轨垂向力时程曲线

由分析结果可知，由于轮轨接触和车辆的二系悬挂特性，扣件失效对乘车舒适性和轨下结构的影响较小，但对钢轨振动影响较大，轮轨振动加剧，轮轨力和轮重减载率均明显增大。扣件正常服役时，350 km·h-1的速度下轮对最大垂向振动加速度为35.652 m·s-2，钢轨最大垂向位移为0.943 mm，钢轨最大垂向加速度为66.20 m·s-2，最大轮轨垂向力和最大轮重减载率分别为85.951 kN 和0.265，当扣件失效时，轮对最大垂向振动加速度为46.266 m·s-2，钢轨最大垂向位移2.777 mm，为正常值的2.94倍，钢轨最大垂向加速度为196.638 m·s-2，为正常值的2.97倍，最大轮轨力和轮重减载率分别为104.872 kN 和0.398，比正常服役状态分别增大了22.0%和50.2%。

在列车荷载作用下，局部扣件失效会造成此区域内的钢轨垂向位移增大，加剧对此范围附近钢轨和扣件的破坏程度，严重时可能影响行车安全。

6 结 语

将钢轨和轨下结构处理为分离的2个子系统，分别建立有限元模型，轨下结构子系统考虑路基、桥梁、隧道等基础设施，钢轨子系统采用2层节点，上层钢轨视为弹性离散点支承的连续梁，下层节点表征扣件，钢轨与扣件间以弹簧-阻尼单元形式连接，在此基础上采用强迫位移和强迫速度的方法处理轨下结构对钢轨的作用。该方法可以更好地反映钢轨的局部振动状态，并可以方便地模拟各类病害对耦合系统动力响应的影响。

应用本文模型对局部扣件失效条件下的列车-轨道-轨下结构动力响应分析表明，扣件缺失将引起轮轨间的局部高频振动，车速350 km·h-1时钢轨最大垂向位移为正常值的2.94倍，钢轨最大垂向加速度为正常值的2.97倍，最大轮轨力和轮重减载率分别较正常值增大了22.0%和50.2%。