Belousov-Zhabotinsky 反应斑图形成的图灵不稳定分析

戴金东， 艾佳莉， 孙 巍

（北京化工大学化学工程学院，北京 100029）

Belousov-Zhabotinsky（BZ）反应是一个非常经典的非线性化学动力学系统。由于反应与扩散的耦合，BZ 反应有着丰富的化学自组织现象，例如时间维度的化学振荡和时空维度的化学斑图等。对于反应扩散系统中化学斑图的研究，艾佳莉等[1]、李才伟等[2]采用偏微分（PDE）模型与元胞自动机模型对BZ 反应进行了模拟，得到了BZ 反应形成的螺旋波等化学波图像。

在丰富的化学斑图中，有一种与动态的化学波有所不同的特殊图像−图灵斑图。图灵斑图是一种逐步产生的定态条纹，前人已经证明了图灵斑图在化学系统中的存在性[3]，并讨论了Brusselator 这一理想化学反应系统产生图灵斑图的数学机理[4]，但是对于实际存在并且在非线性化学动力学中最为经典的BZ 反应，鲜有人讨论图灵斑图产生的条件。

理论上，在一个体系中只要同时存在反应与扩散两种机制，就可以通过反应速率方程和扩散系数写出该体系对应的数学模型，而图灵斑图就是对应的反应扩散方程的平衡解经历了“由扩散引起的不稳定性”之后，产生的稳定的、非一致的空间结构。图灵斑图的现象存在于化学与生物体系中，比如铝在酸性电解液中作为阳极被氧化时形成的多孔氧化铝，就是一种图灵斑图[5]，其过程实质上是一个反应扩散过程，其形成机理可以用斑图动力学来解释；再比如浮游生物在水中的分布，也可以用反应扩散模型来表示，进而以斑图的形式呈现出浮游生物在水中的分布规律[6]。本文对BZ 反应进行了图灵不稳定分析，用图像展示了BZ 反应中图灵斑图的可能形态。BZ 反应是一种简单的反应扩散体系，对BZ 反应中图灵不稳定的研究可以为其他复杂的反应扩散体系提供参考。

1 BZ 反应及其图灵不稳定分析

1.1 BZ 反应模型的建立

BZ 反应的机理非常复杂，经过不断简化最终得到了五步三变量的俄勒冈机理模型[7]。俄勒冈机理模型认为BZ 反应丰富的时空有序现象是由HBrO2、Br−、Ce4+这三种关键物质的不断相互转化实现的，通过写出这三种物质的反应速率方程，以及经过量纲为一处理可以得到现在普遍使用的Tyson模型：

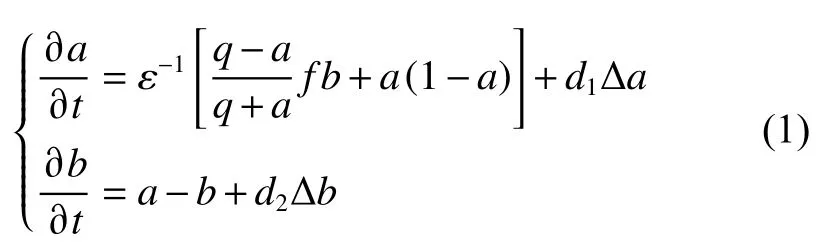
其中 ∆a 与 ∆b 为扩散项：

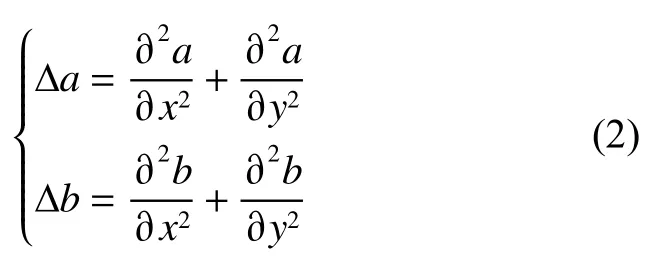
方程组（1）包含2 个变量与5 个参数，且变量与参数均在化简过程中经过了量纲为一化，其中a 代表HBrO2的浓度，b 代表Ce4+的浓度（但a、b 并不等同于浓度）。ε、f、q 是反应动力学参数，其中ε 是与初始浓度以及温度相关的参数，其取值一般在0～1 之间；q 是只与温度相关的参数，其取值一般也在0～1 之间，并根据经验其值一般远小于1；f 是一个可调参数，其取值一般在0～5 之间。d1、d2为两种物质的扩散系数。t 为时间，x、y 分别表示横、纵坐标。

这里只考虑物质在二维平面上的扩散，因此可以规定 x ∈[0,L] 和 y ∈[0,L] ，其中L 为x 和y 所能取得的最大长度。L 的长度在模拟时取400 个空间步长（h），可以模拟出完整的图灵斑图或化学波图案，并通过多次模拟试验得到结论：当 h ≤1 时可以得到较为连续、不失真的模拟图像。空间步长也就是单位步长，使用有限差分法进行模拟时会对每单位步长采用拉格朗日公式处理以近似替代对应点的导数值。为方便计算，后文在验证计算结果时取h=1，L=400进行模拟。

可以看出，当Tyson 模型不考虑扩散项时，系统是一个常微分（ODE）系统，物质浓度仅随时间的变化而变化；当Tyson 模型考虑扩散项时，系统是一个偏微分（PDE）系统，物质浓度同时随时间和位置的变化而变化。

图灵不稳定是指平衡解在不考虑扩散项的ODE 系统中稳定，在考虑扩散项的PDE 系统中变得不稳定的一种情况[8]，因此图灵不稳定分析要分别在两个系统下讨论平衡解的稳定性。

1.2 BZ 反应ODE 模型及其平衡解的稳定性分析

首先写出不考虑扩散项的Tyson 模型：

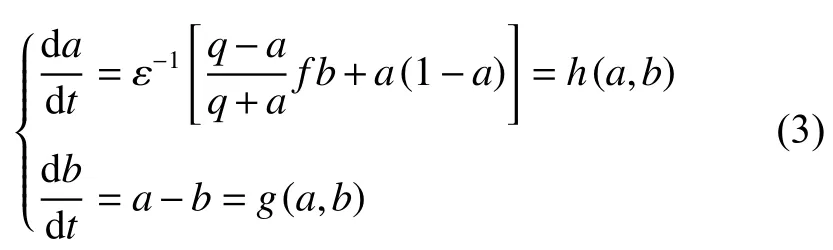
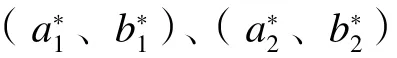
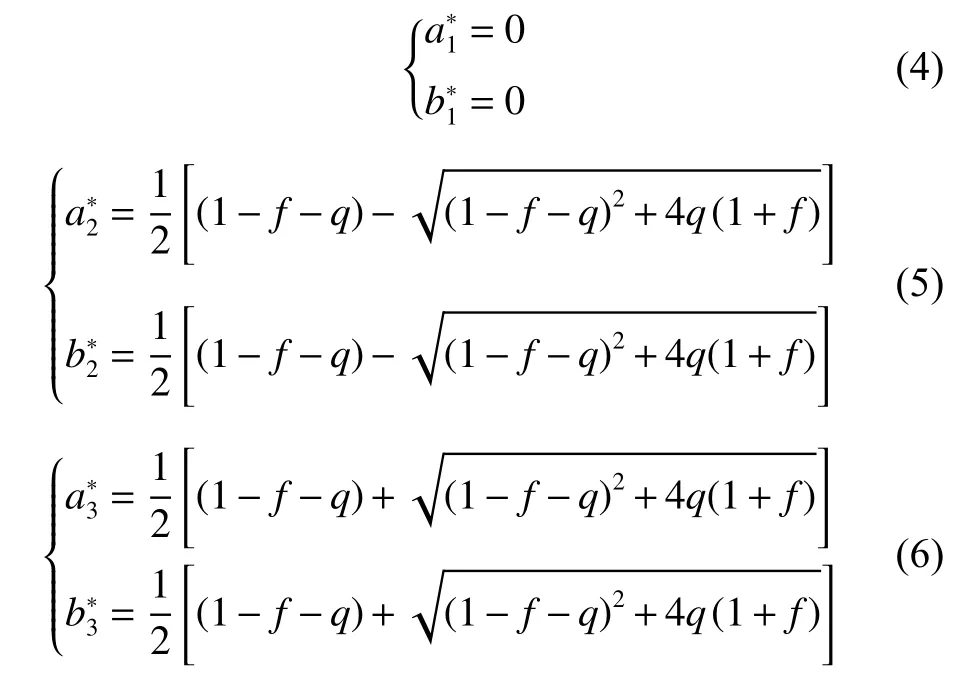
系统在平衡点附近受到的扰动同样可以写为式(3)的形式，只不过需要再将平衡解代入到系数中，以表示是在平衡点附近受到的扰动：

其中系数矩阵为：

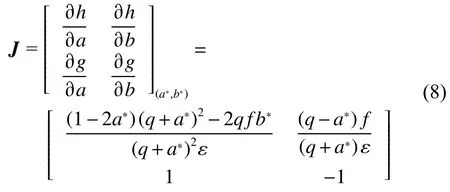
至此就将对微分方程的分析转化为对系数矩阵的分析，系数矩阵的特征方程为

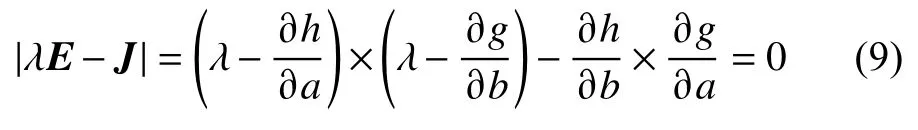
式（9）可以表示为：

其中T 为矩阵的迹，即矩阵对角线之和，D 为矩阵行列式的值，分别如式（11）和式（12）所示。

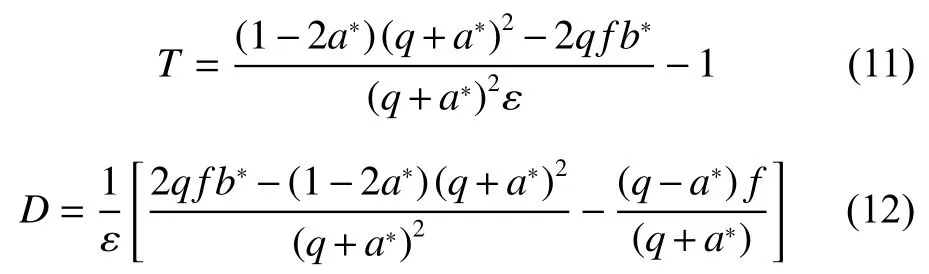
当系数矩阵的特征值均为负数时，对应的平衡解在系统中是稳定的[6]，而通过判断矩阵的迹与行列式值的正负，就可以得到特征方程对应的二次函数曲线图，将3 组平衡解分别代入到T 与D 之中，观察对应的特征方程可以得到结论：第1 组平衡解（a1*，b1*)的特征值为一正一负，不管参数取何值，该平衡解均不能在ODE 系统中保持稳定；第2 组平衡解（a2*，b2*)对应的物质浓度出现了负值，不符合常理；而第3 组平衡解（a3*，b3*)的稳定性与参数的取值相关，接下来详细讨论第3 组平衡解。

根据特征方程，使特征值均为负数的条件可以等价于使矩阵的迹小于零、矩阵的行列式的值大于零，即只需要让各参数满足 T <0 、 D>0 这两个条件，就可以说明此平衡解是稳定的。

为计算使第3 组平衡解在ODE 系统中保持稳定的参数范围，首先计算使 D>0 的参数范围，将第3 组解代入到D 的表达式中可以得到：

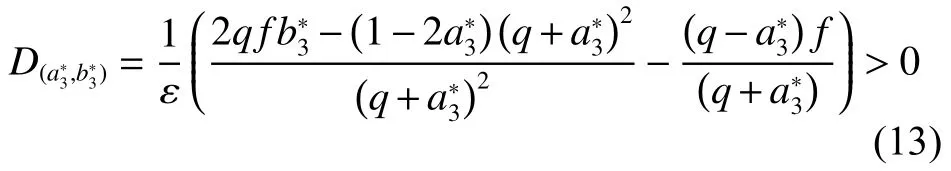
显然对于该式，当q>0 且q ≪1时，f 在0～5 之间取任何数都可以保持 D>0 。接下来计算使 T <0 的参数范围，将第三组解代入到T 的表达式中可以得到：

化简该不等式便可以得到BZ 反应图灵不稳定分析的第1 个参数限制条件：

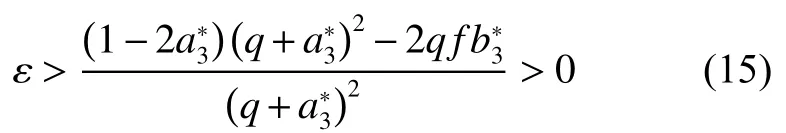
对于第3 组平衡解，只要参数的取值满足式(15)，则该平衡解在ODE 系统中是保持稳定的。

1.3 BZ 反应PDE 模型及其等价转化

对于Tyson 模型，在考虑扩散项之后，系统会变为更加复杂的偏微分方程组。为了应用Routh-Hurwitz判据对平衡解的稳定性进行分析，必须先对偏微分方程组进行转化。

Routh-Hurwitz 判据[9]给出了一种判断数学模型解的稳定性的方法，对于两变量的常系数常微分方程组，其解的形式固定为 C1eλ1t+C2eλ2t，即系统受到的扰动可以写为这种解的形式，其中C1与C2为常数，由初始条件确定，t 为时间， λ1与 λ2为方程组对应系数矩阵的特征值。当两个特征值均为负实数时，系统受到扰动之后，只要经过足够长的时间（t→∞）总会使扰动对状态的影响变为0，即系统总会回到原来的状态，这时该状态是稳定的；若两个特征值不全为负数，则该平衡状态是不稳定的。

对于考虑扩散项的BZ 反应Tyson 模型，需将其向两变量常系数常微分方程组转化。首先将系统在平衡点附近受到的扰动写为微分方程组的形式，然后将平衡解代入到该方程组的系数中，使原来的方程组变为一个常系数偏微分方程组，并写出考虑扩散项的Tyson 模型：

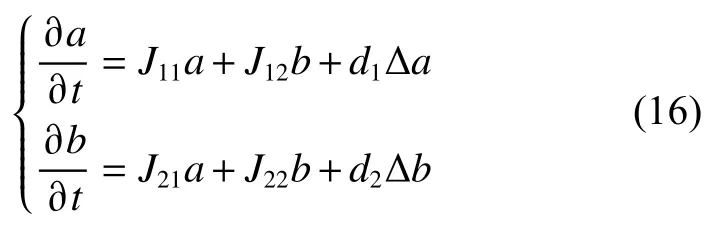
与1.2 节的处理方法相似，此处认为a 与b 为系统在平衡点附近受到的扰动，其中 J11、 J12、 J21、J22均与ODE 系统中的系数相等。

为了使用Routh-Hurwitz 判据，需要继续将方程组向两变量常系数常微分方程组的形式进行等价转化，为此将方程组的解写为傅里叶级数的形式：

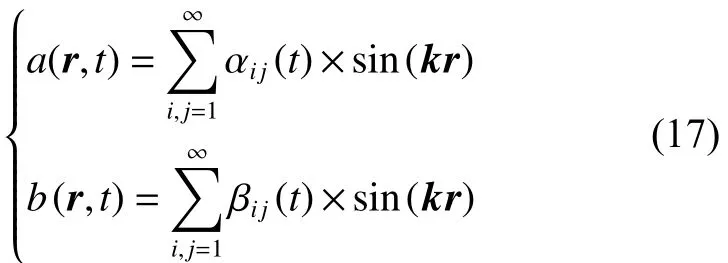
其中k 与r 均为矩阵， k=kikj， r=[x y]T，其中 ki、kj称为波数，且 ki=iπ/L ， kj= jπ/L ，这里只考虑物质在二维平面上的扩散，因此可以规定 x ∈[0,L] 和y ∈[0,L]。将方程组的解代入式(16)中可以得到：

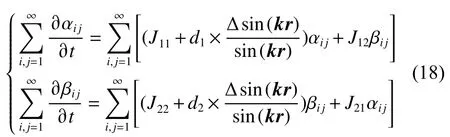
其中 αij和 βij表示对应项的变量。

再对 ∆sin(kr) 做一个处理：

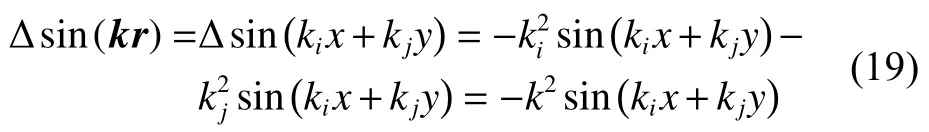
最终可以得到一个与式(16)等价的方程组：

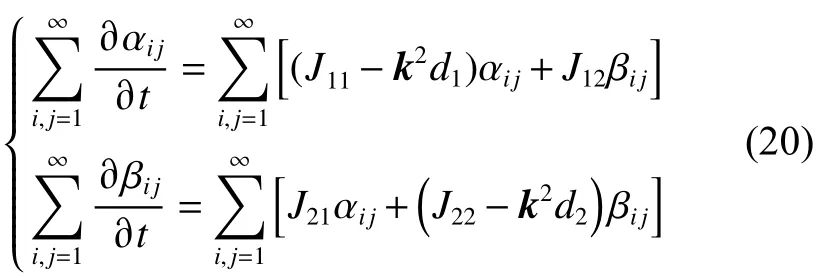
该方法称为分离变量法，通过傅里叶级数展开的方法将偏微分方程组转化为多个常微分方程组求和的形式，再将该方程组对应的新的系数矩阵提取出来：

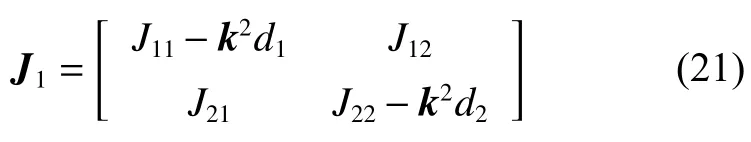
至此就完成了从偏微分方程到常微分方程、从常微分方程到系数矩阵的转化，之后再进行与1.2 节相似的处理就可以得到使平衡解在考虑扩散项的PDE系统中变得不稳定的参数范围，并且BZ 反应模型用傅里叶级数变换得到的系数矩阵与文献[10]中Lotka-Volterra 混合离散反应扩散模型使用不同的处理方法得到的系数矩阵具有相同的形式，由此可以证明该系数矩阵的正确性。

1.4 平衡解在PDE 系统中的稳定性分析

新的系数矩阵的迹 T1与新的系数矩阵的行列式的值 D1为：

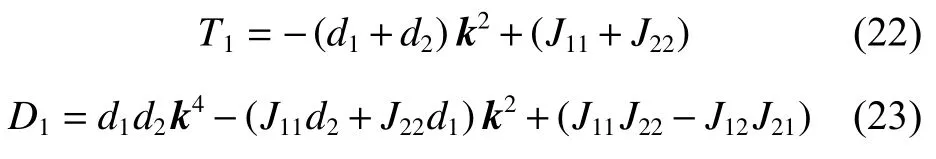
与第1.2 节的处理方式相同，当系数矩阵的两个特征值均具有负实部时，系统是稳定的，而目前计算的是由于扩散项的加入使平衡解变得不稳定的参数范围，因此 T1<0 与 D1>0 这两个条件中至少有一个条件不满足。首先对 T1进行处理：

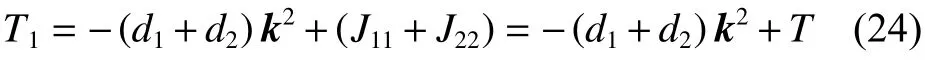
保持平衡解在常微分系统中稳定时，满足T <0，因此 T1<0 依然成立。即若产生图灵不稳定，则参数的取值一定要满足 D1≤0 ，这也是保持平衡解在常微分系统稳定的基础上偏微分系统唯一需要满足的条件。对 D1进行处理：

其中 J11J22−J12J21=D ，D 为1.2 节中常微分方程对应系数矩阵的行列式的值，保持平衡解在常微分系统中稳定时满足 D>0 ，即 H(k2) 对应的二次函数曲线的截距为正值，此时要使 H(k2) 对应的二次函数曲线在 (0,+∞) 上存在低于x 轴的部分，需满足两个条件：（1）二次函数曲线的对称轴在y 轴右边；（2）二次函数存在两个实根，即判别式大于或等于零，这两个条件写为数学表达式即为

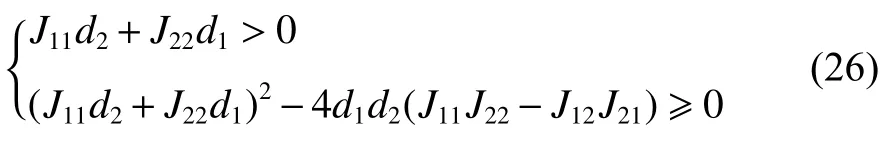
该不等式组表明了使BZ 反应产生图灵不稳定的5 个参数之间的限制条件，只要一组参数符合以上3 个条件，则系统将会发生图灵不稳定。在验证该条件时，需要取出一组满足不等式组的参数值，可以采用固定参数的方法，即首先固定q，再在计算出的f 的取值范围中取一个f 值，然后根据式(15)化简出ε 的取值范围，比如q=0.000 8，f=0.9，ε=0.77 就是一组满足第1 个不等式的可选参数。再根据已选参数对式(26)进行化简，最后选择一个d1的值，则对应一个d2的边界条件。为使计算结果更加直观，可以通过作三维图像的方法，固定q、f、ε 这3 个参数，得到由扩散系数d1与d2组成的图灵不稳定参数范围图像，如图（1）所示。

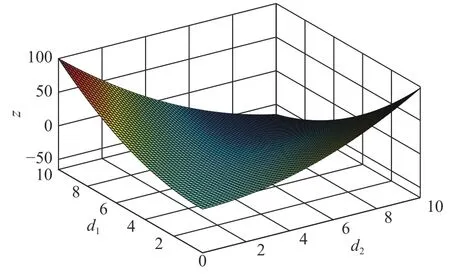
图1d1 与 d2 的取值范围Fi g.1Value range of d1 andd2

图1 中纵坐标表达式为z=(J11d2+J22d1)2−4d1d2(J11J22−J12J21)，即式(27)中第3 个不等式，在此三维界面上如果取一组d1与d2使函数值z >0 ，且满足 d1< 0.989 6d2，则系统产生图灵不稳定，此时系统对应产生的图像应为图灵斑图，即自发产生空间定态条纹。需要说明的是，这一套计算方法与计算结果有待验证。

2 对BZ 反应图灵不稳定的模拟验证

采用数值模拟的方法对BZ 反应进行模拟，首先对设置条件进行说明。初始条件中除了区域中心点（中心点 a 与 b 为任意值）外，区域中其他处a 与b 的值均为零，边界条件采用循环的边界条件，最后对数学模型采用区域离散化与有限差分法，区域离散化将连续的区域近似替代为离散的区域，有限差分法则通过拉格朗日公式将两点间函数的导数近似为两点间的斜率，从而将微分方程组近似替代为代数方程组，以便于求出方程组的近似解。模拟时取空间步长h=1，在400×400 的网格区域进行模拟。

基于以上思路在Matlab 中编写出BZ 反应的模拟程序，进而对不同参数下的BZ 反应现象进行模拟。这里只对b(r, t)的变化进行模拟，即可呈现出不同参数下BZ 反应所产生的图像。因为b 是量纲为一变量，所以在模拟时没有对应的单位。模拟时用颜色表示物质浓度，浓度越高越接近黄色，浓度越低越接近蓝色。

根据1.4 节的计算结果，在固定q=0.000 8，f=0.9，ε=0.77， d1=2 的情况下， d2∈(4.457,+∞) 时系统产生图灵不稳定。图2 所示是在固定q、f、ε、d1这4 个参数下取 d2=5 时的模拟结果。可以看出，当参数取值在图灵不稳定范围内时，反应系统从中心开始缓慢出现一圈又一圈的环形定态条纹，模拟结果验证了计算结果的正确性。

为完善模拟结果，固定q=0.000 8，f=0.9，ε=0.77，d1=2，取 d2=7 进行模拟，结果如图3 所示。发现同样在图灵不稳定参数范围内，当固定的4 个参数取值相等时，两个扩散系数d1、d2相差越大，则系统出现斑图的速度越快。

固定q=0.000 8，f=0.9，ε=0.77， d1=2 ，取d2=2进行模拟，结果如图4 所示。可以看出与前两组不同，系统并没有产生空间定态斑图，而是出现了物质浓度由内向外的动态扩散现象。因此认为只有当参数取值在图灵不稳定参数范围内时，系统才会产生定态斑图，反之则不会产生。

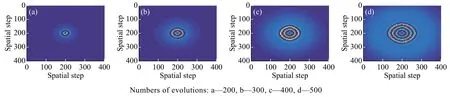
d1=2 d2=5Fig.2Simulation result when and图2、 时的模拟结果d1=2d2=5

图3d1=2 、 d2=7 时的模拟结果Fig.3Simulation result when d1=2 andd2=7

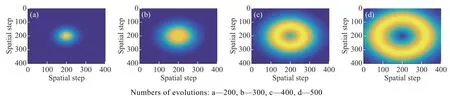
图4d1=2 、 d2=2 时的模拟结果Fig.4Simulation result when d1=2 andd2=2

3 结 论

（1）以BZ 反应扩散系统为研究对象，对反应的数学模型进行了图灵不稳定分析，计算了使BZ 反应产生图灵不稳定的参数限制条件，并作出三维图像以直观表现出计算结果。

（2）使用Routh-Hurwitz 判据对平衡解的稳定性进行判断，使用傅里叶级数展开对偏微分方程进行处理，最后通过数值模拟对计算结果进行了验证，得到了BZ 反应产生图灵不稳定时所呈现出的定态斑图图像。

（3）模拟结果证明了所使用的计算方法与得到的参数范围是正确的。