基于Tri-training MPLS 的半监督软测量模型

李 东， 刘乙奇， 黄道平

（华南理工大学自动化科学与工程学院，广州 510641）

在工业生产领域，由于生产过程的复杂性，存在大量的难以测量或不易检测的重要参数。针对这一问题，软测量技术提供了一个有效的解决方案[1-3]。近年来，软测量技术广泛应用于单输出系统的预测，对多输出预测模型的研究极少[4]。然而，在复杂的生产过程中，急需对多个难以测量的重要参数进行同时预测[5-6]。在众多的软测量建模方法中，目前常用的软测量建模方法有基于机理建模的方法、基于数据驱动建模的方法以及两者相结合的混合建模方法[7]。基于机理建模的方法需要掌握生产过程的详细信息和生化反应原理，对于复杂的工业生产过程而言获取较为困难，使得建立相应的机理模型变得极为不易。基于数据驱动建模的方法则只需要通过一些已知的数据以及这些数据的内在联系构建软测量模型，因此，基于数据驱动的建模方法得到了广泛的关注[8-9]。

在实际的工业过程中，受到现有技术和生产环境的束缚，很多情况下已标记样本数量有限，如何充分使用未标记样本来提升模型质量成为当务之急。为解决这一难题，Shahshahani 等[10]首次提出了半监督学习的思想，并成功应用于软测量建模[11-13]。半监督学习方法利用少量的标记样本构建模型，然后通过未标记样本训练模型，提高模型质量。然而，在训练过程中，由于无法剔除错误的未标记数据，导致错误累积，影响模型的预测能力。为挑选合适的未标记数据训练模型，Blum 等[14]提出了协同训练算法，通过两个相互独立的回归模型，采用交叉验证的方法挑选数据，训练模型。

为了提高多输出模型中数据选择的正确性，本文提出了一种新的软测量模型——Tri-training MPLS模型。该模型通过3 个具有不同特征的回归模型对未标记数据进行验证，挑选出置信度最高的未标记数据训练模型，建立更准确的软测量模型。此外，该模型能够对多个难测量变量进行同步预测，提高了预测效率。通过污水处理仿真模型BSM1 平台验证，结果表明，当标记样本的比例较少时，Tri-training M PLS 模型具有更好的预测性能。

1 预备知识

1.1 多输出偏最小二乘算法（MPLS）

MPLS 算法是在PLS 算法框架上的多数扩展，不同之处在于输出数据Y 由原来的单列向量转化成了多输出矩阵。数学过程如下：

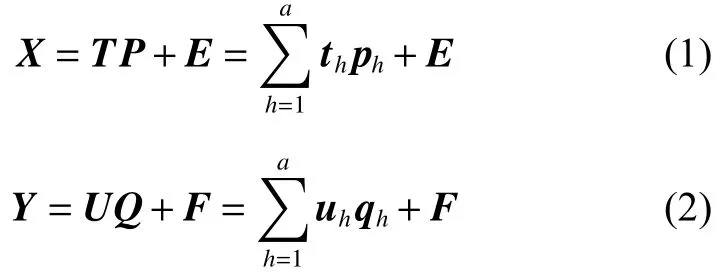
其中： X ∈Rn×m和 Y ∈Rn×l分别为输入和输出矩阵， n为数据集的个数， m 为输入变量的个数， l 为输出变量的个数； T ∈Rn×a和 U ∈Rn×a分别是X 和Y 的得分矩阵，a 表示潜在的变量个数； th为T 的第 h 行； uh为 U 的第 h 行； P(a×m) 和 Q(a×l) 为加载矩阵； ph是 P 的第 h 行； qh是Q 的第h 行；E 和F 为噪声矩阵 。 uh和 th之间的关系如下：

其中： bh为X 空间主元t 和Y 空间主元u 的内部相关 关 系的回归 系 数； U=TB , B ∈Ra×a表示回 归 矩阵。因此，X 和Y 之间的关系可以表示为 Y=TBQ+F 。

MPLS 是一种常见的多元统计分析方法，不仅可以减少数据的维度，还可以建立预测模型，是解决工业 过程中数据预测问题的有力工具[15-16]。

1.2 协同训练回归

其中： xi∈L 为标记输入数据； yi∈L 为标记输出数据；L 为标记样本集， | L| 为样本集大小； h 为原始回归 模型； h′为 加 入 新的 标记 数据 xu后产 生的 回归模型。

协同训练回归根据协同训练的思想建立两个相互独立的初始模型，在验证过程中，采用交叉验证的方式，减少对错误数据的选择。当达到最大迭代次数时，由最终的标记样本集建立模型 h1和 h2，预测值由两者的均值决定：

2 Tri-training MPLS 模型

2.1 Tri-training 回归

式中： hi、 hj、 hk是3 个独立的回归模型。

在多输出系统下，输出数据 y 由原来的单列向量变为多列矩阵，均方根误差（RMSSD）的求解公式如 下：

式中：trace 是矩阵的迹。

当达到最大迭代次数时，由最终的标记样本集建 立模型 h1、 h2、 h3，预测值由三者的均值决定：

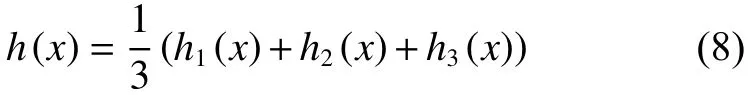
2.2 Tri-training MPLS 应用于软测量建模

Tri-training MPLS 模 型 的 核 心 是 将Tri-training算法和MPLS 算法相结合生成对多输出系统的软测量模型。其优势在于，首先，由上述的置信度判断依据选择正确性更高的未标记数据，模型的预测效果更好；其次，通过标记数据集建立3 个相互独立的回归模型，使得预测模型具有广泛性；最后，Tri-training MPLS 模型能够同时对多个输出变量预测，极大地提高了预测的效率和模型的整体性。

Tri-training PLS 模 型 的 具 体 过 程 如 下：设L={X,Y}={(x1,y1),(x2,y2),···,(x|L|,y|L|)} 表 示 标 记 数据集， | L| 表示标记数据集个数， U 是未标记数据集，|U| 表示未标记数据集个数。首先，将L 平均分成3 部分，记为L1、L2、L3，将L1、L2、L3与传统的偏最小二乘算法结合生成相互独立的3 个回归模型P1、P2、P3。然后，取未标记数据集U 中的数据 xu，分别代入到P1、P2、P3中计算回归量。在学习过程中，用其中两个回归量的均值来更新另一个标记样本集。随着迭代的进行，该过程不仅不断地建立3 个相互独立的回归模型，而且在差异越来越大的回归量上更新标记数据集。为了选取合适的未标记数据，利用上述方法估计未标记数据的置信度，然后对满足置信条件的未标记数据计算回归量，将两个回归量的均值作为新的标记数据放入另一个标记样本集中。最后，由新的标记样本集L1、L2、L3建立新的模型h1、h2、h3，通过求取3 者均值作为最终的预测值。Tritraining MPLS 的详细流程如下：

输入: 标记样本集L (包含输入变量 xl和输出变量 y )，未标记样本集U（仅包含输入 xu），测试样本集P，最大迭代次数T

过程：

进行T 次迭代:

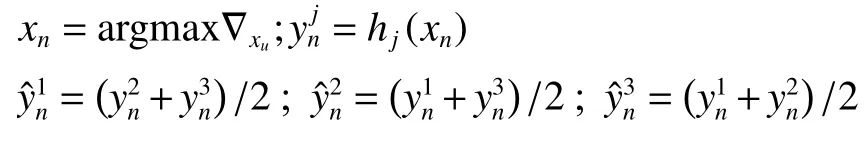
然后 U=U −xn

U=U

否则

πj=∅

End of for

Lj=Lj∪πj

达到最高迭代次数，结束迭代

输出新的标记样本集 L1、 L2and L3

for j ∈{1,2,3} do

hj=pls(Lj)

end of for

验证模型预测能力：

为比较Co-training MPLS 模型和Tri-training MPLS模型算法的复杂性，图1 示出了两种模型的流程图。由图1 可知，两种模型的算法都被分为训练环节和测试环节两部分，不同之处在于训练环节中，Cotraining MPLS 模型将标记数据均分为两部分，由两组标记数据子集同时评价未标记数据的置信度。而Tri-training MPLS 算法是将标记数据三等分，有3 组标记数据子集同时评价未标记数据的置信度，并选择置信度较高的未标记数据加入到标记数据集中。3 个相互独立的标记样本子集同时训练，避免了因单个数据级判断错误而影响选择的质量，致使错误累积，最终导致预测结果较差。从算法复杂度的角度分析，无论是2 组标记子集还是3 组标记子集，训练过程是一致的，只是Tri-training MPLS 算法的训练时间会相对较长。

为了评价Tri-training MPLS 模型的预测性能，采用传统的均方根误差（RMSE）和D 值指标评价，定义如下：

3 仿真实例

污水处理仿真模型BSM1 平台的设备布局如图2 所示，由一个生物反应器(5999m3)和一个二次沉淀池(深4 m,10 层,6000 m3)组成。生物反应器包含5 个混合小单元，前2 个单元（每个1000m3）为非曝气的，后3 个单元（每个1333m3）为曝气的。处理污水的平均流量为20000m3/d，可生物降解的化学需氧量(COD)的平均质量浓度为300 mg / L。为了去除有机物，需要进行硝化和反硝化反应[20-21]。

图1Co-training MPLS（a）和Tri-training MPLS（b）模型的流程图Fig.1Flow chart of Co-training MPLS (a) and Tri-training MPLS (b) models

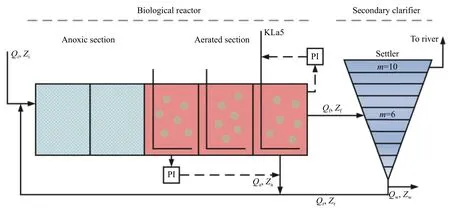
图2BSM1 平台设备布局示意图Fig.2Schematic diagram of BSM1 platform equipment layout

仿真过程中，共纳入了15 个输入变量和5 个输出变量，详细的变量信息如表1 所示。本案例的研究目的是验证Tri-training MPLS 模型对SS-E、SNH-E、SNO-E、COD-E 和BOD5-E 等不易测量变量的预测性能。每隔15 min 对各个变量采样一次，模拟14 d，共1344组数据。分别将第1 天、第2 天、…、第7 天的样本作为已标记数据集，剩余部分作为未标记数据集，最大学习次数设置为5 次。最后，用剩余7 d的数据作为测试样本集，对模型进行测试。

图3 示出了标记样本为4 d 时两种模型的预测曲线和D 值。可以看出，Co-training MPLS 模型和Tri-training MPLS 模型均能够同时对多个输出变量进行预测，且预测效果良好，尤其是对污水排放指标中的重要参数BOD5-E 的预测，RMSE 值分别达到了0.08 和0.07，预测曲线与真实值基本一致，其他具体参数见表2。MPLS 算法作为一种线性建模方法，显然对于波动较大的输出数据的预测性能较差，特别是预测曲线中的峰值点和谷值点，都没有达到良好的预测结果。

图4 示出了输出变量RMSE 值的变化曲线图。通过表2 和图4分析，当标记数据所占天数仅为1 d时，Tri-training MPLS 模型中的SS-E、SNO-E、COD-E和BOD5-E 的RSME 值 均 小于Co-training MPLS 模型的RSME 值。因此，在标记数据极少的情况下，Tri-training MPLS 模型对于污水处理过程中的重要指标参数的预测能力优于Co-training MPLS 模型。但观察发现，在标记数据为1 d 时COD-E 的Cotraining MPLS模 型 和 Tri-training MPLS 模 型 的RSME 值分别为257.12 和64.37，明显偏大。随着标记数据所占天数的增加，各个输出变量的RMSE 值均在减小，尤其是COD-E 的RSME 值由257.12 和64.37 迅速减小到2.49 和2.50。这说明当标记样本较少时，对于波动较大的输出变量，Co-training MPLS 模型和Tri-training MPLS 模型需要通过少量的标记数据将建立2 个或者3 个回归模型，导致模型不准确，预测表现不佳。当标记数据充足时，两个模型均能通过标记数据建立更准确的预测模型，并且通过未标记数据训练模型，对多个输出变量进行精

准的预测。综上所述，在仅仅具有少量的标记数据情况下，Tri-training MPLS模型对多个输出变量的预测效果优于Co-training MPLS 模型；当标记数据增多时，两种模型的预测表现差别不大。

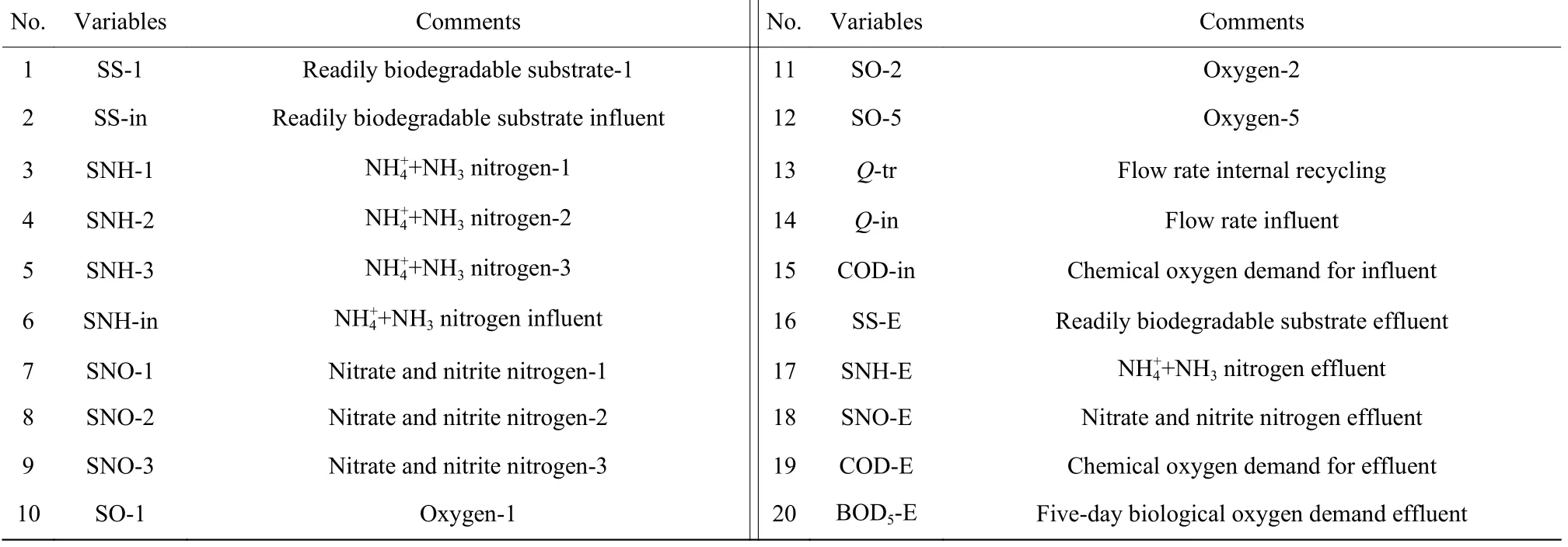
表1BSM1 平台中的变量Table1Variables of the BSM1 platform

图3两种模型的预测曲线和DFig.3Prediction curves and D of two models

表2输出变量的RSME 值Table2RMSE values of output variables

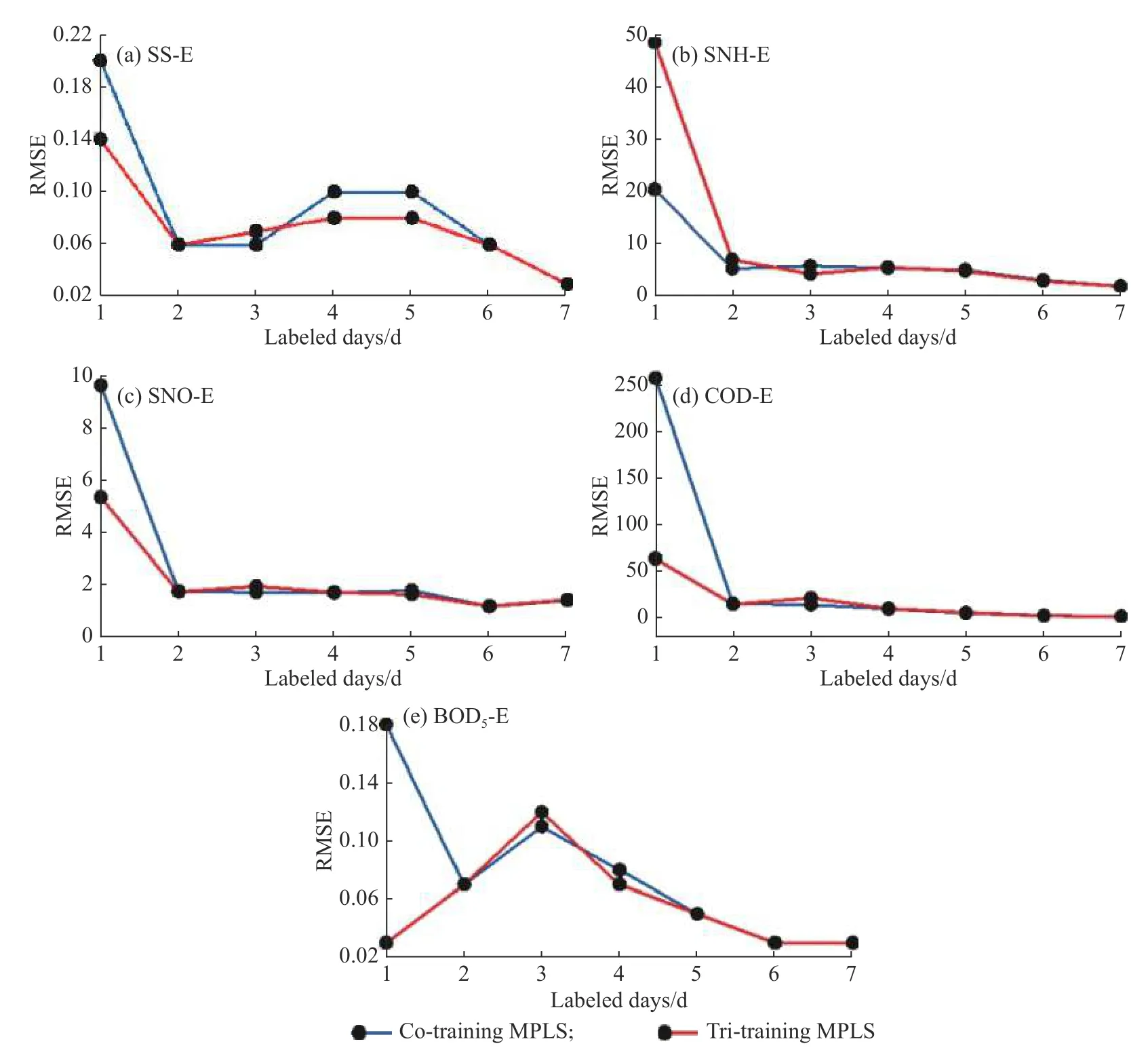
图4不同标记样本率下的RMSE 变化曲线Fig.4RMSE curves under different labeled data rates

表3 列出了两种模型在不同标记样本率下的时间消耗对比结果。无论是Co-training MPLS 模型还是Tri-training MPLS 模型，随着标记样本率的增加，时间消耗也在增加。在相同的标记样本率下，Tri-training MPLS 模 型的 时间 消耗 相对 于Co-training MPLS 模型有所增长，这主要是因为3 组标记数据子集的训练要比2 组费时，但是Tri-training MPLS 模型的预测结果较好。

表3不同的标记样本率下的时间消耗Table3Time consumption under different labeled data rate

4 结 论

针对多输出系统中的软测量建模问题，当输入和输出数据严重不平衡时，本文提出了一种新的软测量模型−Tri-training MPLS 模型。通过污水处理仿真模型BSM1 平台的仿真研究，验证了模型的有效性。仿真结果表明，虽然Tri-training MPLS 模型在预测时间上相较于Co-training MPLS 模型有一定的滞后，但在预测效果上却有明显的提升，尤其是对重要的出水指标COD-E，其RSME 值比Co-training MPLS 模型平均减小26.46。该模型为多输出系统中难以测量的变量预测问题提供了一个有效的解决方法。然而，不难发现，模型对于峰值点和谷值点的预测效果不佳。在实际的工业生产过程中，也会存在着正常波动和离群点，影响模型的预测表现。针对这一问题，下一步的研究会将Tri-training 算法与非线性的多输出回归算法结合，并且，在建模之前对数据进行标准化处理，以降低因数据波动对预测表现造成的影响。