考虑视场角约束的三维时间控制制导律

阮 聪，温求遒，张文杰

(北京理工大学 宇航学院，北京 100081)

0 引 言

随着现代武器防御系统的快速发展，制导弹药的战场生存能力以及毁伤能力面临严峻挑战[1]。为了减小作战消耗，提高制导弹药的突防能力，饱和齐射攻击的作战方式越来越受到重视，而实现饱和攻击的一个关键技术就是时间控制制导技术[2]。

自从饱和攻击作战方式被提出以来，国内外研究者提出了许多不同形式的时间控制制导律。Jeon等人[3]针对非线性运动模型，提出了一种平面内基于广义比例导引的时间控制制导律。Tekin等人[4]基于前置角成型技术，提出了一种需要迭代求解菲涅尔积分的时间控制制导律。文献[5]基于剩余飞行时间估计，给出了一种构造时间控制制导律的通用设计方法，并应用到考虑落角约束的时间控制制导律的设计中。Kim等人[6]利用李雅普诺夫稳定性理论，提出了一种平面内的非线性攻击时间控制制导律，并推广到三维空间中。He等人[7]考虑误差收敛的最优动力学，提出了一种三维最优时间控制制导律，避免了平面时间控制制导律由于空间耦合引起的末端制导指令抖振问题。考虑到导引头实际视场的限制，为避免由于制导弹药机动引起的目标丢失问题，文献[8]提出了平面内满足视场角约束的时间控制制导律，但是存在控制指令奇异问题。陈升富等人[9]基于滑模控制技术，提出了一种考虑视场角约束的无奇异点攻击时间控制制导律。杨哲等人[10]基于多项式函数推导了不依赖剩余飞行时间估计的时间控制制导律，通过引入视场角函数反馈项实现视场角约束。文献[11]针对地面固定目标，提出一种考虑视场角约束的两阶段复合时间控制制导律，并且分析了攻击时间可达域。Chen等人[12]设计切换滑模面，通过终端滑模控制技术实现了视场角受限的切换时间控制制导律。上述大多数同时考虑攻击时间和视场角约束的制导律都只是针对平面制导问题，没有考虑到空间角度耦合问题，而针对三维空间的时间控制制导律又没有考虑视场角约束。因此，现有的时间控制制导律很难直接应用到三维饱和式攻击场景中。

基于以上研究，针对制导弹药饱和式攻击问题，基于经典三维比例导引，考虑偏航和俯仰通道的耦合，提出一种考虑空间视场角约束的三维时间控制制导律。

1 制导弹药三维拦截模型建立

假设制导弹药是一个速度恒定的可控质点，图1给出制导弹药三维空间内攻击静止目标的几何示意图。坐标系OXIYIZI和MXVYVZV分别为惯性坐标系和弹道坐标系，M和T分别为制导弹药和静止目标，V为制导弹药速度，az和ay分别为制导弹药的俯仰和偏航加速度，R为弹目相对距离，θL和φL分别为弹目视线俯仰和偏航视线角，θm和φm分别为制导弹药速度在俯仰和偏航方向的前置角，σ为总的速度前置角。

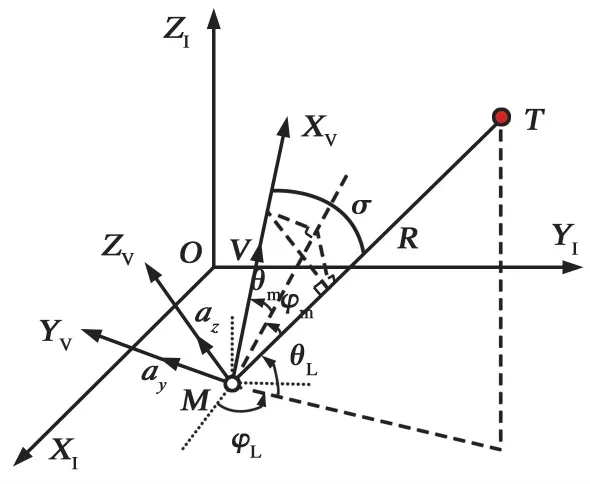
图1 三维攻击几何关系Fig.1 Three dimensional interception geometry

根据制导拦截几何关系，三维空间内攻击固定目标的弹目相对运动数学模型[13]为

(1)

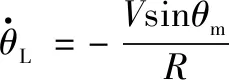
(2)

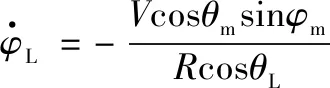
(3)

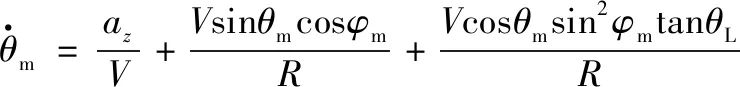
(4)

(5)

cosσ=cosθmcosφm

(6)

通常情况下制导弹药的攻角和侧滑角相对较小，可以直接忽略，则导引头的视场角约束可以近似等效为总的速度前置角约束[8,14]。假设σmax为导引头视场范围决定的视场角边界值，则导引头视场角约束可以描述为

|σ|≤σmax

(7)

因此，本文所研究的满足视场角约束的三维时间控制制导律可以描述为设计满足式(8)的俯仰和偏航通道加速度指令，使得制导弹药在满足视场角约束的情况下能以指定攻击时间命中目标：

(8)

式中：td为指定攻击时间。

2 三维时间控制制导律设计

2.1 考虑视场角约束的时间控制制导律设计

为了实现考虑视场角约束的攻击时间控制制导要求，制导弹药必须同时满足命中目标约束、视场角约束以及攻击时间约束。

基于三维比例导引弹道的剩余飞行时间估计为[7]

(9)

式中：N为比例导引系数，一般取值在3～6之间。

考虑剩余飞行时间估计精度对制导律攻击时间控制精度的影响，下面在三维比例导引律的基础上，考虑一种新的满足视场角约束和攻击时间控制的偏置比例导引律：

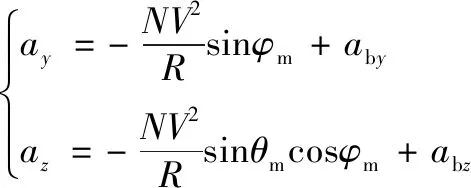
(10)

式中：aby，abz分别为满足视场角约束以及攻击时间的偏航和俯仰加速度指令偏置项。

对式(6)求导，并联立式(4)～(5)，(10) 得

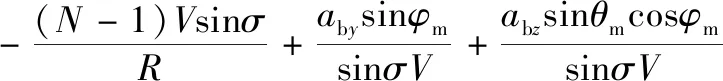
(11)

基于式(9)，定义攻击时间误差滑模面：

s=td-t-tgo

(12)

对式(12)求导，并联立式(11)得

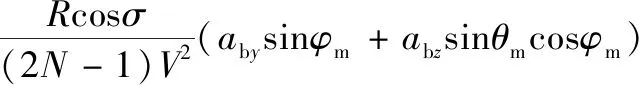
(13)

由于导引头视场角约束，速度前置角σ通常较小，因此，基于小角假设：

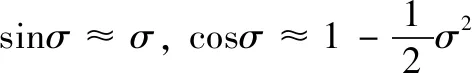
(14)

将式(14)代入式(13)中，并忽略高阶小项得

(15)

结合式(15)，基于滑模控制理论，偏航和俯仰加速度指令偏置项设计为

(16)

式中：k>0为偏置项控制增益，符号函数为

结合式(10)和式(16)，考虑视场角约束的三维时间控制制导律为

(17)

值得注意的是，当攻击时间误差s≠0时，即使制导弹药指向目标(σ=0)，aby和abz均不为0，即俯仰和偏航偏置项依旧可以起到攻击时间调节作用。考虑到比例导引常数一般取值为3，则制导律的调节参数只有一个，有利于工程中制导控制增益调节。

2.2 稳定性分析

假设末制导初始时刻导引头捕获目标，制导弹药的速度前置角满足视场角约束，即：|σ0|≤σmax。采用式(17)所示的制导律能使制导弹药在末制导过程中满足视场角约束，并且攻击时间误差是收敛的。

为了证明制导弹药末制导过程中满足视场角约束，定义集合Ψ={σ:|σ|≤σmax}，选取李雅普诺夫函数：

(18)

对式(18)求导，并联立式(11)得

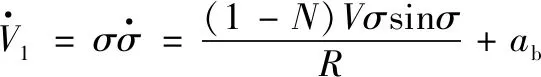
(19)

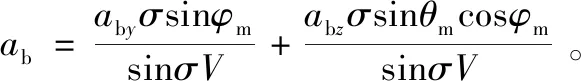
当σ→0 时，φm→0 且θm→0，有

(20)

由式(20)知，σ→0不会使式(19)引起奇异问题。考虑集合Ψ边界上的点：当|σ|=σmax，有ab=0。则当比例导引系数N>2时，以下不等式恒成立：

(21)

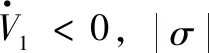
下面证明制导律能够使剩余飞行时间误差收敛。选取李雅普诺夫函数如下：

(22)

对式(22)求导，并联立式(15)～(16)得

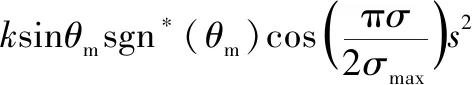
(23)

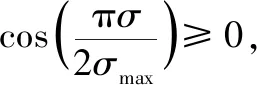
当增益k取值足够大时，s会在有限时间ts收敛到0，记ts时刻弹目距离和前置角分别为Rs,σs。联立式(1)、式(6)和式(11)有

(24)

(25)

综上所述，所提出的制导律式(17)能够使制导弹药同时满足视场角约束、命中约束以及攻击时间约束。并且，当末制导初始时刻制导弹药直指目标时，该制导律仍能对攻击时间起到调节作用。

3 仿真分析

针对制导弹药在三维空间中攻击固定目标的场景，进行了仿真验证。目标位置为(5 000,5 000,0) m，制导弹药初始位置为(0,0,0) m，速度为250 m/s，初始俯仰和偏航前置角分别为10°和-15°。导弹俯仰和偏航方向可提供的最大加速度均为8g，其中g=9.8 m/s2。制导律设计参数为：N=3，k=20，仿真步长选为0.01 s。为了减小符号函数在末制导末端引起的抖振现象，当剩余飞行时间误差小于0.2 s时，采用tanh函数来代替符号函数，其函数表达式为

其中，a为设计参数，取值为0.1。

设定制导时间分别为30 s和35 s，视场角约束分别为40°和45°，仿真结果如图2所示。

以上仿真条件下，攻击时间控制误差不超过0.001 s，脱靶量不超过0.01 m。结合图2(a)所示的弹道曲线表明，不同视场角约束下，制导弹药均能以指定攻击时间精确命中目标，并且指定攻击时间越大，弹道越弯曲。图2(b)～(c)所示的剩余飞行时间误差曲线和视场角曲线表明，制导弹药末制导段能满足视场角约束，剩余飞行时间误差逐渐收敛，并且指定攻击时间越长，最大视场角约束越小，则制导弹药以最大视场角飞行时间越长，剩余飞行时间误差收敛越慢。结合图2(d)～(e)所示的过载曲线，制导弹药弹道主要分三段：初始阶段攻击时间误差大，制导弹药以最大过载调节弹道；随后触碰最大视场角约束，过载迅速减小，制导弹药以最大视场角飞行；最后由于剩余飞行时间误差收敛，制导律退化为三维比例导引，视场角和过载逐渐收敛到0，增强末端抗干扰能力。

图2 不同约束下仿真结果Fig.2 Simulation results of different constraints

针对不同制导时间和视场角约束条件，图3给出了分析不同偏置项控制增益k对剩余飞行时间误差收敛速度的影响。仿真结果表明：对于不同的制导时间和视场角约束条件，偏置项控制增益k越大，剩余飞行时间误差收敛速度越快；同时，随着k的增加，剩余飞行时间误差收敛速度的增长速率逐渐变缓。

图3 不同增益下剩余时间误差Fig.3 Time-to-go errors of different gains

图4表明，采用两种制导律，制导弹药均能以指定攻击时间精确命中目标，并且当指定攻击时间小时，两种制导律弹道性能差异不大。图4(b)～(c)表明，随着攻击时间增加，尽管文献[6]中制导律攻击时间误差收敛较快，但是其最大视场角接近90°，远远超过导引头的视场范围，容易导致制导弹药丢失目标。图4(d)～(e)所示的过载曲线表明，两种制导律末端过载均收敛到0，随着指定攻击时间增大，尽管文献[6]快于本文所提出的制导律过载收敛速度，但是其过载饱和时间也明显较长。从表1所示的控制能量对比结果可以看出，当攻击时间较小时，两种制导律控制能量接近，但是随着攻击时间增加，本文所提出的制导律控制能量明显小于文献[6]中制导律控制能量。

表1 控制能量对比Table 1 Control effort comparison

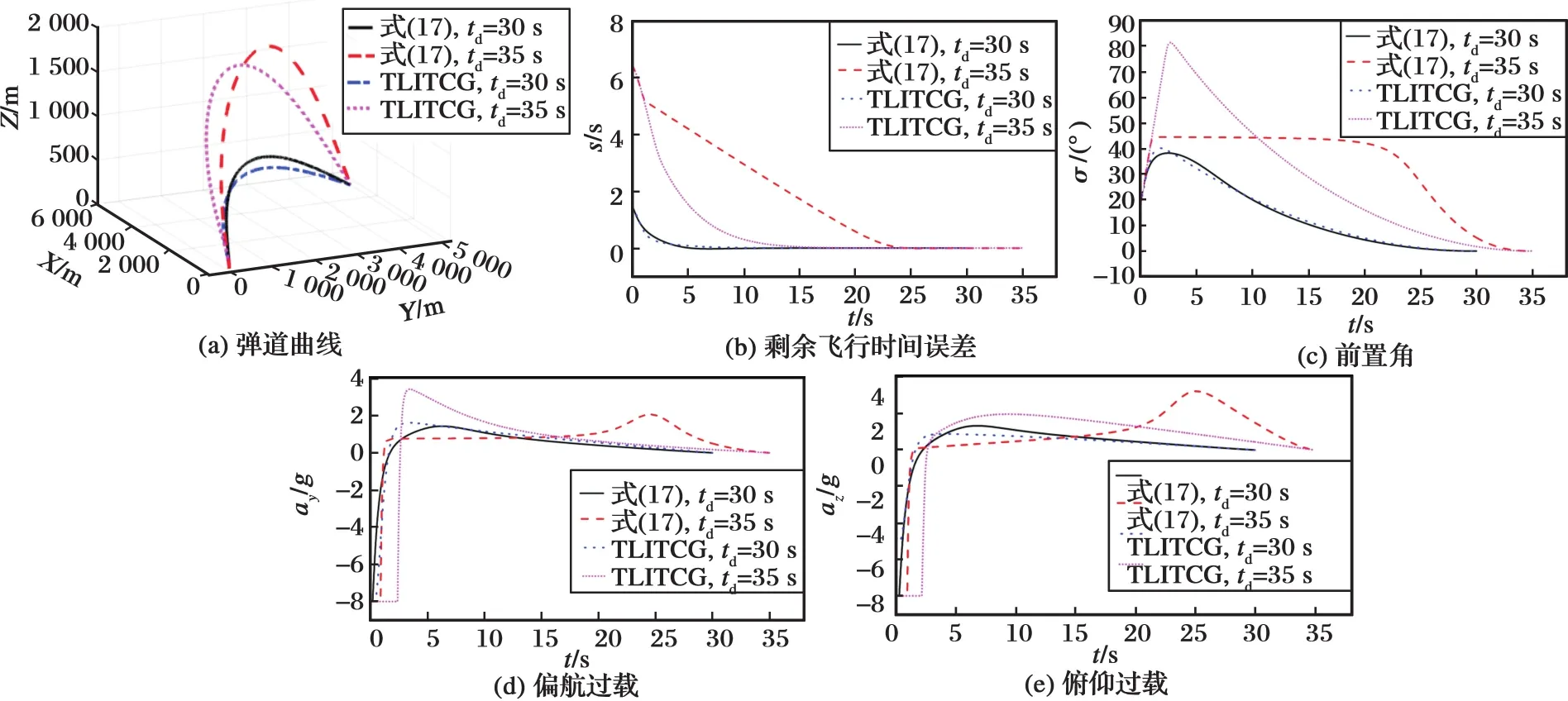
图4 制导律对比Fig.4 Comparison of guidance laws

4 结 论

针对制导弹药在三维空间中的饱和式攻击问题，基于经典三维比例导引律，提出了一种考虑空间视场角约束的三维攻击时间控制制导律。该制导律由比例导引项和满足空间视场角约束的攻击时间误差反馈附加项组成，通过理论分析和仿真对比可得出如下结论：

(1) 基于李雅普诺夫理论，本文给出了满足视场角约束和攻击时间误差收敛的严格稳定性证明；

(2) 本文所提出的制导律在不同仿真条件下，能够满足空间视场角约束，并且实现了以期望攻击时间对固定目标的精确打击，末端过载逐渐收敛，控制能量消耗较小。