航班流时空分布不均衡程度评价方法

王剑辉，李翰之

(中国民用航空飞行学院，四川 广汉 618307)

航班流是指航空器在空域内连续飞行形成的交通流。在航班流的航班数量一定的情况下，航班流在空域内时空分布的不均衡，会造成管制员的负荷增加、空域利用率低等结果。对航班流的分布科学分析研究，制定一系列的战略和战术管理措施，可以有效地降低管制员负荷，提高空域利用率并且增加航班流运行的安全性。而航班流的时空分布均衡性是航班流分布的重要特征，定量评价航班流时空分布的不均衡程度是分析研究航班流时空分布特征的第一步。

戴文雯等[1]运用智能仿真工具对终端区空中交通特性进行了定性分析。袁立罡[2]对终端区动态的交通特征进行分析，并且对其运行态势进行了研究。许炎等[3]研究了空中交通流的时空特性，揭示了交通流内在联系以及拥堵的机理。岳仁田等[4]对扇区繁忙时段交通流的不均衡度进行了量化研究，但只对空间分布进行了研究，没有涉及时间分布上的不均衡分析。因此，提出利用基尼系数和泰尔指数量化评价航班流时空分布均衡程度的方法，考虑时间分布和空间分布的均衡性，对航班流的时空分布不均衡程度分析，以实际运行数据为例进行分析论证。

1 不均衡指标概述

1.1 泰尔指数概述

泰尔指数(Theil index)来源于物理学，又称泰尔熵指标，是由经济学家Theil利用信息理论中熵的概念于1976年提出的评价收入公平性的指标[5]。泰尔指数作为广义均衡性评价工具，其使用范围已经远超出经济领域，近年来被广泛应用在医疗卫生、资源配置、道路建设和城市轨道交通等领域[6]。

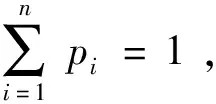
(1)

将信息论中的熵理论用于评价收入差距时，可解释为将人口份额转化为收入份额时消息所包含的信息量，泰尔指数T的数学表达式为

(2)

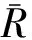
1.2 基尼系数概述

1921年意大利经济学家基尼(CorradoGini)在洛伦兹曲线的基础上提出的基尼系数(Gini coefficient)作为广义均衡分析的工具,不但国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标,而且可以用于描述财产、资本、产 品、市场等资源分配的均衡程度[8]。

洛伦兹曲线以家庭或者人口的累积百分比为横轴，相应分组家庭或者人口的收入累积百分比为纵轴,构成一个面积为1的正方形图形,其对角线 被称为“绝对平均直线”，如图1所示。洛伦兹曲线下凹程度越大,收入分配越不平均;反之,下凹程度越小,实际分配的平均程度越高[9]。基尼系数G表示为洛伦兹曲线与绝对平均线包围面积A占绝对平均线与绝对不平均线包围面积A+B的比重[10]，即

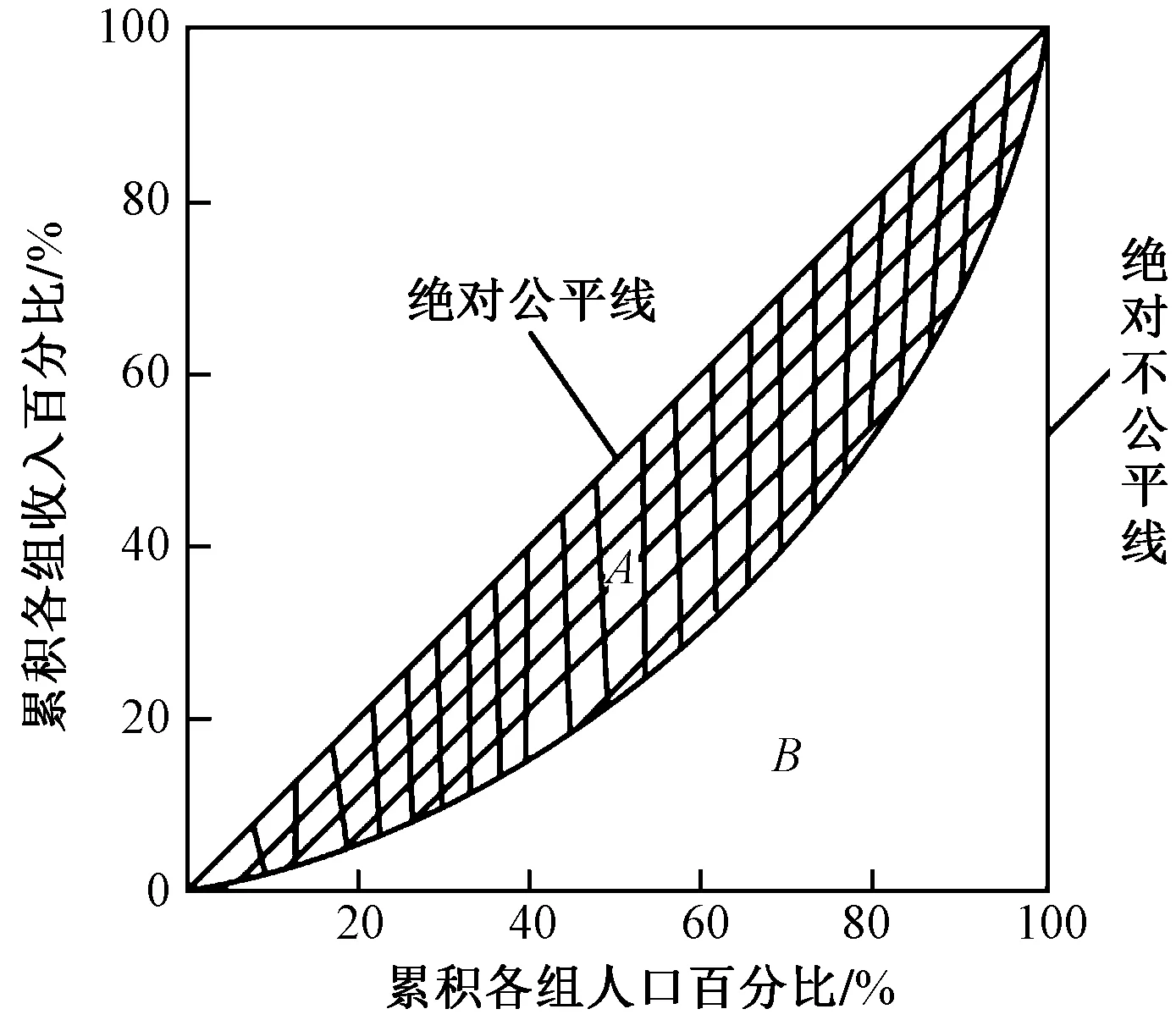
图1 洛伦兹曲线

(3)

式中，G为基尼系数；A为实际洛伦兹曲线与绝对平均线所包围的面积；B为洛伦兹曲线与绝对不公平线之间的面积。

G∈[0,1]，G越大表示越不平均，联合国制定了基尼系数表1所示的评价标准。

表1 国际基尼系数评价标准

2 航班流时空分布不均衡程度评价

对航班流在时间t内在空域x时空分布的不均衡程度评价。假设航班流在时间t内分布在空域x的航班数量是F。把时间段t分为m段，终端区由n个扇区组成；xi为第i个扇区，i=1,2,…,n；tj为第j个时间段,j=1,2,…,m；F为航班流t内在A的分布数量；Fxit为航班流t内在xi的分布数量，i=1,2,…,n；Fxtj为航班流tj内在x的分布数量，j=1,2,…,m;Fxitj为航班流tj内在xi的分布数量，i=1,2,…,n；j=1,2,…,m。

2.1 空间分布不均衡度计算方法

计算tj时间段内，航班流在空域x内各扇区xi的分布数量间的泰尔指数Ts，把Ts定义为航班流时空分布的泰尔空间不均衡度，可以用Ts来表征航班流空间分布的不均衡程度。

根据泰尔指数的计算公式可得各个tj时间段内的Ts，即

(4)

计算tj时间段内，航班流在空域x内各扇区xi的分布数量间的基尼系数Gs，把Gs定义为航班流时空分布的基尼空间不均衡度，可以用Gs来表征航班流空间分布的不均衡程度。

步骤1把Fxitj从小到大排列，得到新的样本集合。

步骤2依次计算各个扇区xi(i=1,2,…,n)内Fxitj的累计百分比φk。从小到大第k个扇区的累计百分比φk计算公式为

(5)

步骤3以tj(j为定值)各个扇区xi(i=1,2,…,n)内Fxitj的累计百分比φ为纵轴，以扇区编号i(i=1,2,…,n)为横轴，每组数据(k,φk)在坐标轴中用一个点表示，做n组数据形成的散点图。

步骤4利用最小二乘法拟合曲线φk=f(k,a)，其中a=(a0,a1,a2,…,an)是拟合参数，误差平方和ε2为

(6)

步骤5计算tj时间段内，航班流在终端区x的空间分布均衡程度也即基尼系数Gs。利用微积分求面积的方法求出tj时间段内的Gs。

(7)

2.2 时间分布不均衡度计算方法

计算航班流在某扇区xi(i为定值)各时间段的分布数量间的泰尔指数Tt，把Tt定义为航班流时空分布的泰尔时间不均衡度，可以用Tt来表征航班流在扇区xi内各个时间段分布数量的不均衡程度。扇区xi的Tt计算公式为

(8)

计算航班流在扇区xi内，各时间段分布数量之间的基尼系数Gt，把Gt定义为航班流时空分布的基尼时间不均衡度，可以用Gt来表征航班流在扇区xi内各个时间段分布数量的不均衡程度。

步骤1把Fxitk从小到大排列，得到新的样本集合。

步骤2依次计算各个时间段tj(j=1,2,…,m)内Fxitj的累计百分比φk。那么从小到大第k个时间段的累计百分比φk计算公式为

(9)

步骤3以xi内各个时间段tj(j=1,2,…,m)的Fxitj的累计百分比φ为纵轴，以时间段编号j(j=1,2,…,m)为横轴，每组数据(k,φk)在坐标轴中用一个点表示，做m组数据形成的散点图。

步骤4利用最小二乘法拟合曲线φk=f(k,a)，其中a=(a0,a1,a2,…,an)是拟合参数，误差平方和ε2为

(10)

步骤5计算基尼系数Gt。利用微积分求面积的方法求出扇区xi各时间段之间的Gt。

(11)

3 实例分析

以国内某飞行情报区为例，该飞行情报区共有9个扇区，以1 h为时间片，将一天分为24个时间片，采集航班流在每个扇区每个时间片的分布数量数据。从空间和时间两个角度对航班流的时空分布的均衡程度进行评价。具体数据如表2所示。t1表示0:00—1:00，t2表示1:00—2:00，以此类推，t24表示23:00—24:00。

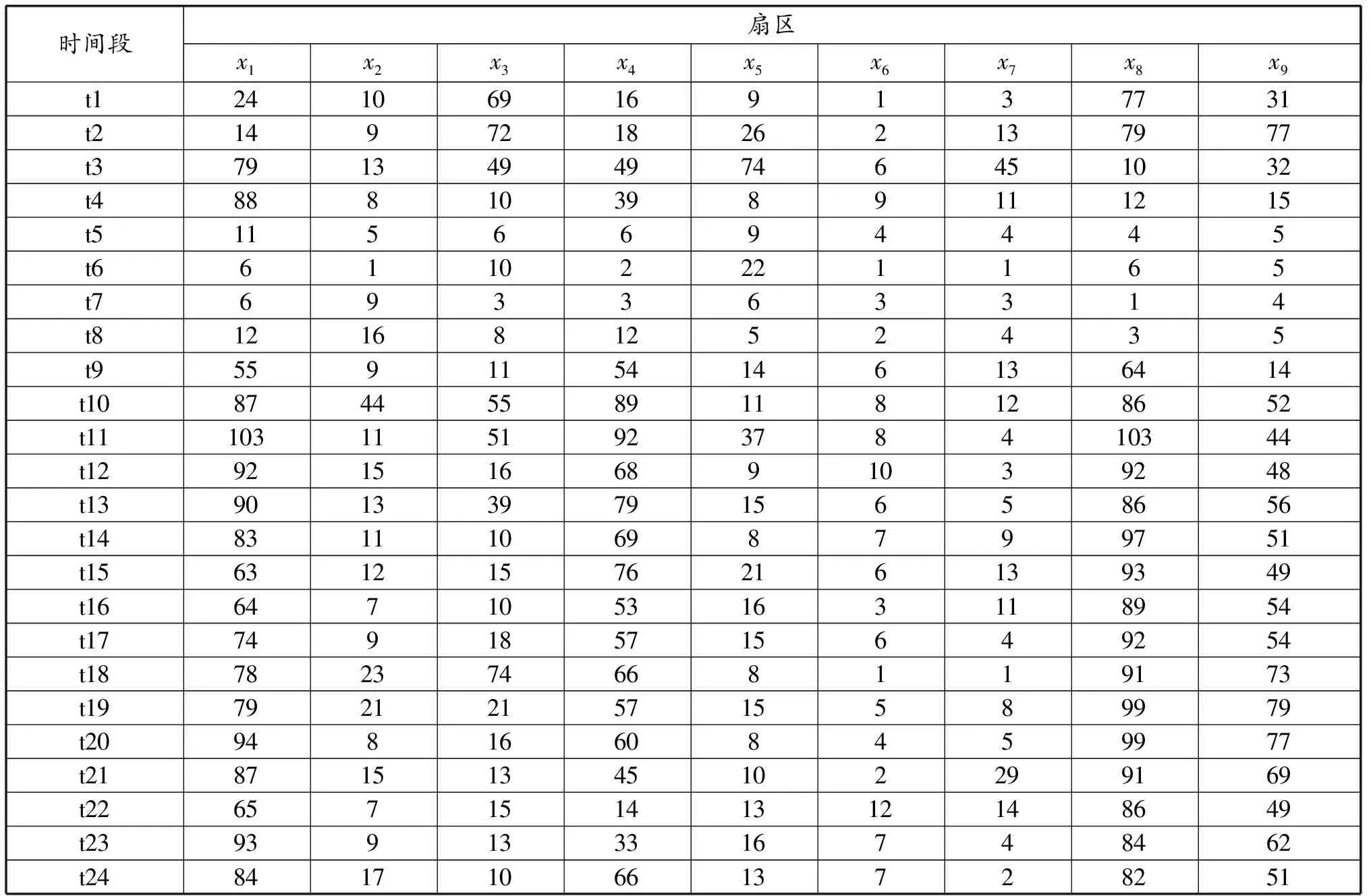
表2 航班流在各扇区各时间段的分布数量

3.1 计算空间分布不均衡度

按照上文叙述的方法，利用MATLAB编程计算该空域内泰尔空间分布不均衡度Ts和基尼空间分布不均衡度Gs。结果如表3所示。将其结果可视化，如图2所示。

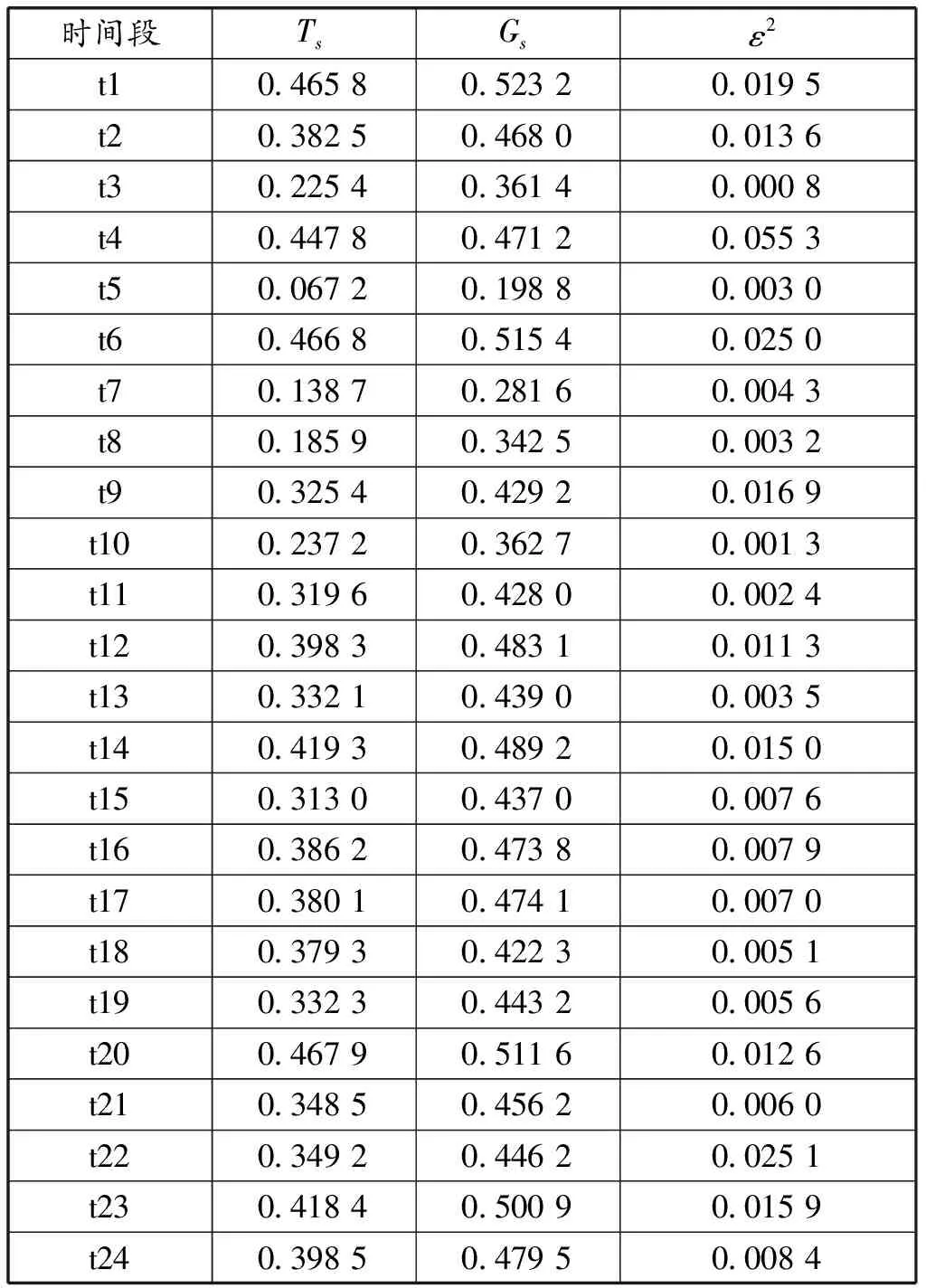
表3 泰尔空间不均衡度Ts和基尼空间不均衡度Gs的计算结果

图2 泰尔空间分布不均衡度Ts和基尼空间分布不均衡度Gs的计算结果

由图2可以清晰看出，0:00—1:00、5:00—6:00、19:00—20:00、22:00—23:00这4个时间段的基尼空间分布不均衡度Gs>0.5，因此结合表1的评价标准可以判定航班流在这4个时间段的空间分布极不均匀，结合表2确实可以看出航班流在这几个时间段内的空间分布不均匀。此外从图中还可以看出航班流在4:00—5:00时间段内，空域的空间分布比较均衡，从表2中可以看出4:00—5:00航班流在各扇区的分布数量都很少，因此它的空间分布也比较均匀。

从图2可以看出泰尔空间分布不均衡度Ts和基尼空间分布不均衡度Gs具有很强的相关性，计算Ts和Gs两组数据的相关系数。两个变量间的相关系数r的计算公式为

(12)

计算得Ts和Gs的相关系数为0.973 4。因此可以判定两组数据极高相关。说明两种计算方式判定的结果是一致的，因此，可以通过计算泰尔空间分布不均衡度Ts和基尼空间分布不均衡度Gs来量化评价航班流空间分布均衡程度。

3.2 计算时间分布不均衡度

按照上文叙述的方法，利用MATLAB编程计算24 h内泰尔时间分布不均衡度Tt和基尼时间分布不均衡度Gt。结果如表4所示。将其结果可视化，如图3所示。

表4 泰尔时间不均衡度Tt和基尼时间不均衡度Gt的计算结果

图3 泰尔时间分布不均衡度Tt和基尼时间分布不均衡度Gt的计算结果

从图3可以看出，0.4≤Gt≤0.5，结合表1国际基尼系数评价标准可知差距较大，即航班流在第3扇和第7扇的各个时间段之间分布比较不均衡。此外从图3还可以看出第6扇的不均衡度较小，通过表2可以发现航班流各个时间段分布在第6扇的数量都比较少，各个时间段的分布数量都比较均衡，因此第6扇的泰尔时间分布不均衡度Tt和基尼时间分布不均衡度Gt都较小。

根据式(12)计算Tt和Gt两组数据的相关系数，可得Tt和Gt的相关系数为0.810 1,可以判断Tt和Gt高度相关，说明两种计算方式判定的结果是一致的，因此，可以通过计算泰尔时间分布不均衡度Tt和基尼时间分布不均衡度Gt来量化评价航班流时间分布不均衡程度。

4 结论

利用泰尔指数和基尼系数评价航班流时间分布和空间分布的不均衡程度。泰尔指数和基尼系数作为广义衡量均衡性的工具，具有深厚的理论基础，应用十分广泛。从空间和时间两个角度来衡量航班流时空分布的均衡性，计算各个时间段空域的空间分布不均衡程度和各个扇区的时间分布不均衡程度，通过论证得到以下结论：

1)泰尔指数和基尼系数计算得到的结果具有很强的相关性，得到的评价结果是一致的；

2)利用泰尔指数和基尼系数可以客观地量化评价航班流时间分布和空间分布的不均衡程度。

3)通过该方法量化得到的航班流在空域内的空间分布和时间分布的不均衡程度，可以为决策者掌握空域内航班流的状态提供参考。