事故树-层次分析法在预防公路爆破飞石中的应用
陈善江
(国家电投集团 广西兴安风电有限公司,广西 桂林 541000)
爆破作为一种高效、便捷的生产手段,被广泛地应用于矿山采掘、土石方开挖、水利航道疏浚等工程。根据相关资料表明,在中国仅就露天矿山爆破飞石事故在整个所有爆破飞石事故中的比例就已达到27%[1],而爆破飞石事故在全国所有爆破施工作业中所产生的事故中占20%左右[2],由此给相关人员和单位造成了巨大的财产损失和人员伤亡。因此,运用安全系统工程中的事故树方法结合层次分析法对影响爆破飞石事故各因素进行分析,得出其中的关键因素,对预防爆破飞石具有重要的现实意义。
事故树分析法(fault accident tree,FAT)是一种应用数理逻辑的方法,从顶上事件开始,结合布尔逻辑门方法,逐步向下找出可能引起顶上事件发生的直接以及间接原因,并分析这些原因之间的关系。事故树分析法是一种以图形作为介质的演绎推理法,具有很大的灵活性,为改善和评价系统的安全性提供了定性依据[3]。
层次分析法(analytic hierarchy process,AHP)是美国匹兹堡大学教授Saaty于1960年左右提出的一种系统分析方法。AHP先分析系统中各个元素之间的相互关系,建立目标层、准则层、指标层结构,继而对同一层次中的各元素关于上一层中的准则的重要性进行两两互相比较。构造判断矩阵,并求出每个元素对应的权重。再通过一致性检验CR<0.1才认为构造的判断矩阵符合一致性要求。符合一致性要求的元素权重就可以进行单项权重排序或者总权重排序[4]。
事故树分析法将需要分析的事件作为顶上事件,逐层寻找引起顶上事件发生的原因,也就是基本事件。随后利用最小割集或最小径集计算各基本事件之间的排序,即结构重要度系数,表征基本事件对顶上事件的影响程度。层次分析法用指标层中各基本因素的合成权重来表示基本元素对目标层的重要程度。但是传统的层次分析法在利用判断矩阵计算权重时,是采用的专家打分法,这样的分析结果完全取决于专家对于整个事件的认知程度,主观意识作用太过于强烈,很多情况下都不满足一致性检验,需要不断地对两两比较的结果进行调整,程序较为繁琐。而层次分析法结合事故树的方法,即事故树分析法中的基本事件与层次分析法中的指标层因素一一对应,利用事故树分析法中的结构重要度来进行两两比较,摒弃专家打分,具有相比于传统层次分析法的客观性与优良性,且一致性检验很容易通过,计算程序也相对简单[5]。
现以某工程作为实例,采用事故树结合层次分析法进行引起爆破飞石事故的基本因素分析,计算出各个因素的权重并进行排序,找出关键的因素并提出相应的预防措施,避免该工程发生爆破飞石事故。
1 工程概况
广西路桥工程集团有限公司承建的融水至河池高速公路二分部路线起于罗城县小长安镇守善村附近,接一分部施工图设计桩号K25+057,终于罗城县四把镇大新村附近,接三分部施工图设计桩号K55+113,项目跨越1县3镇和数个村屯,沿线地方关系和情况错综复杂,主线全长28 km。
1.1 地质条件
该区地层主要由石炭系、泥盆系碳酸盐岩灰岩、白云岩、硅质灰岩组成,除洼地及谷地中有薄薄的黏土覆盖外,其余基岩裸露,厚度随基岩变化。爆区为石炭系大埔阶白云岩,中风化为主,局部表面有薄层强风化层,厚层-块状,与边坡关系为顺向斜交。该边坡为岩质路基,为峰林谷地工程地质区。具体爆破位置如图1所示。

图1 爆破区域位置
1.2 工程难点
此次爆破区域为K53+950~ K54+50地段,该地段为山体土石方爆破开挖,爆破区域山体净高20~34 m,爆破周边区域环境较为复杂,北偏东侧110 m左右有一个村庄,有大量古老破旧的土坯房,且这些土坯房正在使用,距离爆破区域65 m左右有一座村民祠堂,该祠堂为砖结构,北偏西方向 320 m 左右有一正在运营的省道,其他方向为使用的田地和荒山。且工程工期较为紧凑严密,在上次爆破作业方向还有大量施工人员进行施工。
爆破作业产生的有害效应包括爆破振动、爆破飞石、爆破冲击波都会影响周边村民的建筑设施。因为作业区域位于山体上,高度相对于村民建筑教高,爆破产生的振动会相应减小,且本工程爆破采用延时爆破,振动和冲击波影响不大。但是一旦发生飞石事故则会造成很严重的影响,如何保证正在使用的老旧土坯房和距离过近的村民祠堂以及该村人民、现场机械设备以及施工人员不受到爆破飞石、滚石的影响,是本工程的一大难点。
利用爆破事故树-层次分析法进行爆破飞石事故的建模,分析造成飞石事故的基本因素,找出权重并进行排序,以此来预防该工程爆破飞石事故的产生。
2 事故树分析
2.1 爆破飞石事故树建立
本工程周边环境错综复杂,且需要保护的建筑和农田以及人员较多,确保不产生爆破飞石飞落破坏民房或农田以及伤害村民是首要任务。将爆破飞石作为顶上事件[6],产生爆破飞石伤害事故一般分为两种情况:一是正常起爆引起的飞石事故,二是非正常起爆引起的飞石事故,分别继续对每一种情况产生的原因层层分析,结合逻辑推理能力,找出引起顶上事件产生的所有最基本事件,绘制相应的事故树,如图2所示。基本事件的含义如表1所示。

图2 爆破飞石事故树
2.2 爆破飞石事故树结构函数
由图2可知,事故树的顶上事件的结构函数为
T=M1+M2=M3+M4+M5+M6=M7+M8+M9×M10+X21+X22+M11+X25+X26+X27=X1+X2+X3+X4+X5+X6+X7+(M12+M13+M14)×(X19+X20)+X21+X22+X23+X24+X25+X26+X27=X1+X2+X3+X4+X5+X6+X7+[X8×(X9+X10+X11)+X12+X13+X14+X15×(X16+X17+X18)]×[(X19+X20)]+X21+X22+X23+X24+X25+X26+X27。
2.3 事故树结构重要度分析
事故树的结构重要度表征基本事件对顶上事件的影响程度,是事故树分析的重要步骤。利用事故树最小割集或最小径集计算结构重要度[7],具体公式为
(1)
式中:k为最小割(径)集数目;m为包含第i个基本事件的最小割(径)集数目;nj为第i个基本事件所属的第j个最小割(径)集中基本事件的数目。
经过计算,本事故树最小割集较为繁多,共有32个割集,为了方便分析,将事故树转换为成功树,利用最小径集计算结构重要度。最小径集共有5个,分别为
P1=(X1,X2,X3,X4,X5,X6,X7,X8,X12,X13,X14,X15,X21,X22,X23,X24,X25,X26,X27);P2=(X1,X2,X3,X4,X5,X6,X7,X8,X12,X13,X14,X16,X17,X18,X21,X22,X23,X24,X25,X26,X27);P3=(X1,X2,X3,X4,X5,X6,X7,X9,X10,X11,X12,X13,X14,X15,X21,X22,X23,X24,X25,X26,X27);P4=(X1,X2,X3,X4,X5,X6,X7,X9,X10,X11,X12,X13,X14,X16,X17,X18,X21,X22,X23,X24,X25,X26,X27);P5=(X1,X2,X3,X4,X5,X6,X7,X19,X20,X21,X22,X23,X24,X25,X26,X27)。
根据式(1)计算各基本事件的结构重要度为
Iφ(1)=Iφ(2)=Iφ(3)=Iφ(4)=Iφ(5)=Iφ(6)=Iφ(7)=Iφ(21)=Iφ(22)=Iφ(23)=Iφ(24)=Iφ(25)=Iφ(26)=Iφ(27)=0.050 8;
Iφ(12)=Iφ(13)=Iφ(14)=0.038 3;
Iφ(8)=Iφ(15)=0.020 1;
Iφ(9)=Iφ(10)=Iφ(11)=Iφ(16)=Iφ(17)=Iφ(18)=0.018 2;
Iφ(19)=Iφ(20)=0.012 5。
3 爆破飞石事故层次分析模型
构建爆破飞石事故层次分析模型,将爆破飞石事故A作为目标层,爆破设计施工B1、地质条件B2、环境及安全管理B3作为准则层,27个基本事件C按照从属关系依次归类到各准则层下作为指标层。层次分析模型如图3所示。
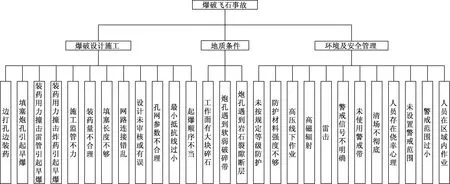
图3 爆破飞石事故层次分析模型
3.1 构造与分析判断矩阵
事故树中的结构重要度表示基本事件对顶上事件的影响程度,层次分析法判断矩阵中的合成权重,也同样表示为对目标层的影响大小,区别就是事故树是基于逻辑演绎原理计算出结构重要度,而层次分析法则只是利用专家主观判断打分作为判断因子而得出合成权重,具有一定的局限性。因此基于结构重要度和判断因子的一致性原则,利用结构重要度构建判断矩阵。目标层下层含有3个准则层B,每个准则层中的结构重要度为各自基本事件的结构重要度的和,利用准则层各自的结构重要度进行两两比较,可以得到目标层A与3个准则层之间的判断矩阵。指标层C中的27个事件的判断因子均利用各自结构重要度进行两两比较表示,并构建准则层B与各自对应的指标层的判断矩阵。判断矩阵中的各判断因子大小按照1-9标度法[8]进行选取,对本例为小数的结构重要度而言,由于1-9标度法中的判断因子需要为整数,所以本模型需要将两两比较前的结构重要度采取四舍五入法进行确定[9]。则目标层A与准则层的判断矩阵如表2所示,同理可得准则层与指标层之间的构造矩阵(由于其中两个准则层下所属的指标层均有12个基本事件,构造判断矩阵比较庞大,限于篇幅,本文省略),并计算各自判断矩阵的最大特征值λmax、权重W、一致性指标CI、平均随机一致性指标RI以及随机一致性比例CR。

表2 目标层-准则层判断矩阵
3.2 计算与检验
计算相应的最大特征值λmax,并根据式(2)、式(3)计算出一致性指标CI与随机一致性比例RI。再计算完CR之后,当CR≤0.1时,则认为所构造的判断矩阵满足一致性检验,当CR>0.1时,则认为所构造的判断矩阵不满足一致性检验,需要重新进行因素比较,直到满足一致性检验为止。
(2)
(3)
式中:λmax为判断矩阵的最大特征值;n为判断矩阵的阶数;CI为一致性指标;RI为平均随机一致性指标;CR为随机一致性比例。
目标层与准则层判断矩阵的计算结果为:λmax=3.001 2,RI=0.52,CI=0.000 6,CR=0.001 2。可以看出此时的CR=0.001 2<0.1,所以目标层与准则层的判断矩阵满足一致性检验。
同理,可以得到3个准则层与其对应的指标层的最大特征值λmax、一致性指标CI、平均随机一致性指标RI、随机一致性比例CR,以及各个基本因素对目标层的影响权重。具体如表3所示。
从表3可知,准则层与指标层判断矩阵均通过一致性检验。为了确定基本因素对目标层的影响大小,结合准则层的权重,需要计算每一个基本因素的合成权重(Xi的合成权重为Wi),计算结果为
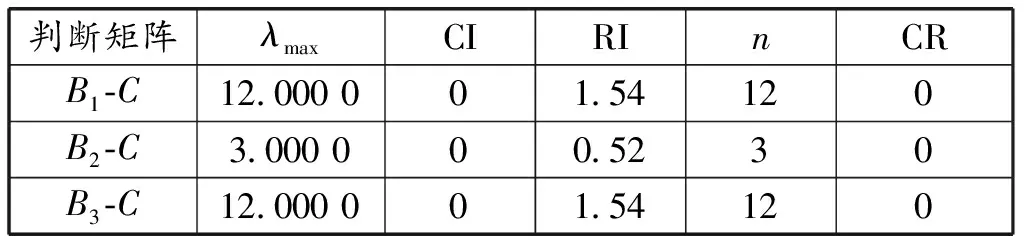
表3 准则层与指标层判断矩阵最大特征值及一致性检验结果
W1=W2=W3=W4=W5=W6=W7=W25=W26=W27=0.0514;
W21=W22=W23=W24=0.050 0;
W12=W13=W14=0.037 3;
W8=W15=0.019 9;
W9=W10=W11=W16=W17=W18=0.017 9;
W19=W20=0.012 9。
4 结果分析与比较
利用事故树分析法得到的各基本事件的重要度排序为
Iφ(1)=Iφ(2)=Iφ(3)=Iφ(4)=Iφ(5)=Iφ(6)=Iφ(7)=Iφ(21)=Iφ(22)=Iφ(23)=Iφ(24)=Iφ(25)=Iφ(26)=Iφ(27)>Iφ(12)=Iφ(13)=Iφ(14)>Iφ(8)=Iφ(15)>Iφ(9)=Iφ(10)=Iφ(11)=Iφ(16)=Iφ(17)=Iφ(18)>Iφ(19)=Iφ(20)。
事故树分析法的重要度排序表明了基本事件X1~X7、X21~X27的结构重要度最大,X12~X14的结构重要度排第二,X8、X15的结构重要度排第三,X9~X11、X16~X18的结构重要度排第四,X19、X20的结构重要度最小。
事故树结合层次分析法得出的各因素合成权重大小排序为
W1=W2=W3=W4=W5=W6=W7=W25=W26=W27>W21=W22=W23=W24>W12=W13=W14>W8=W15>W9=W10=W11=W16=W17=W18>W19=W20。
事故树结合层次分析法排序结果与单纯事故树排序结果类似,W1~W7、W25~W27为影响权重最大,W21~W24次之,W12~W14合成权重排第三,都为0.037 3,其影响也不能忽视,其余排序与事故树分析法一样。
综合现场实际情况分析,事故树结合层次分析法所得的结果更加符合实际。所以工程应该特别注重加强人员安全的管理,做好划定警戒范围以及清场彻底的措施,包括清理现场的施工人员、大型设备、附近爆破警戒范围内的所有村民。提前清理工作面大块碎石,当遇到软弱破碎带以及岩石裂隙层时应该重新设计好爆破参数,注重预防因外来杂散电流而引起早爆事故的发生,避免产生飞石造成人员伤亡事故。
5 结论
1)采用事故树结合层次分析法来分析爆破飞石事故,利用事故树的结构重要度来构建层次分析法的判断矩阵,能够避免专家打分的主观意识作用,更加具有科学性和客观性。
2)利用逐层递进的关系,找出飞石事故的27个基本事件,建立了事故树模型和层次分析法模型,利用结构重要度构建判断矩阵,对爆破飞石事故做了定性和定量分析。
3)综合基本因素的权值大小来看,影响此工程爆破飞石事故的最主要因素为爆破区内有未撤离或者误入的人员(X1~X7)。其次为因外来杂散电流和爆破员操作不当引起的早爆(X21~X27)因素。所以重点加强现场人员安全管理以及附近村民的疏散是工程预防爆破飞石事故至关重要的措施。

