深度数学教学 提升核心素养

陈素霞 尤婉清

深度数学教学，旨在引导学生在已有学习经验的基础上，进一步挖掘表层知识所蕴含的内在含义与数学逻辑。深度教学模式下，教师应引导学生通过质疑争辩、独立思考、合理迁移以及信息联结等一系列方式，提高自己思考、辨析、归纳等思维能力，从而提升核心素养。

一、基础练习精选素材，深入交流中唤醒学生思维

数学课堂承载的远非知识本身，更重要的是思维训练。学习素材是课堂教学的重要载体，是促进学生思维发展的重要平台。数学课堂中教师精选有深度的学习素材，引领学生步步深入学习，教会学生掌握知识的同时，更让他们学会深度思考，拓宽思维空间。

如在教学“三位数乘两位数练习课”时，笔者出示基础练习的题目：笑笑参加演讲比赛，演讲时的平均语速为每分钟215个字，需要演讲15分钟，笑笑准备了3000字的稿子，够吗？学生思考并解题后，生1首先回答：“我用竖式计算215×15=3225（字），3225>3000，笑笑准备3000字够了。”教师追问：“竖式计算中，每一步是怎么来的？表示什么意思？结合题目意思说说看。”（学生反馈略）生2：“215×15≈200×15=3000（字），把215估小，已经是3000字了，而准确结果一定比3000大，215×15>3000，所以我认为够。”生3：“215×15≈200×20=4000（字），4000>3000，所以够。”笔者：“看来用估算的方法也能解决问题。第三个同学的估算能说明问题吗？”生4：“不能，把215估小成200，把15估大成20，4000有可能比准确的结果大，也有可能比准确的结果小。”笔者追问：“对比第二种方法的估算和第一种方法的精算，哪种办法会更快解决问题呢？”生5：“估算比较合理，会更快捷省时，精算的办法也可以，就是需要细心计算，比较慢。”

在上述片段教学中，看似一道简单的练习，笔者让学生依据自己的思考方法去解题;同时，留给学生思考交流的时间、空间，每个学生在这样一个自主思考、深度交流、对比辨析的过程中，收获的不仅是自己的“战利品”，还有令自己意外的“果实”。在今后的学习中，他们会主动观察数字的特点，开始思量不同方法的优劣，思维得到了提升。

二、提高练习串点成线，深度学习中引发数学思考

教学中，我们不难发现，大部分数学知识是建立在已有旧知之上，多数学生会运用已知经验来学习当前的知识，懂得意会却不懂表达出来。教师在课堂中，应对学生存在的这种混沌的思维加以点拨、引领，沟通前后认知的联系，促进学生新旧知识意义同化的发生，形成有意义的学习。

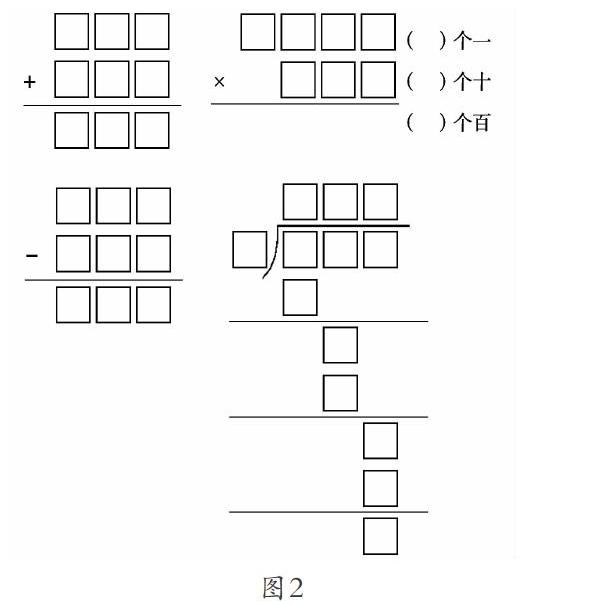
如在“三位数乘两位数练习课”的提高练习中，笔者设计了以下组串练习：13×2，13×12，138×12。这三道题，数字虽小，但数位逐渐增加。笔者先引导学生逐题地口头表达算法，如第一题中，学生列完竖式说：先算2×3得到6个一，再算2×10得到2个十，最后把6个一和2个十合并起来是 26。笔者此时结合课件适时出现横式“2×3=6，2×10=20，13×2=26”。学生以同样方法口头表达出第二题和第三题的算法，在充分完整表达算法的过程中，深度理解整数乘法的算理。笔者顺势追问：“同学们猜想一下，接下去会是几位数乘几位数呢？”学生纷纷举手，有说三位数乘三位数的，也有说四位数乘三位数的，还有说五位数乘四位数的。笔者趁热打铁，借助课件适时出现没有数字、只有方框的四位数乘三位数的乘法算式（图1），追问：“这样的四位数乘三位数会算吗？”学生略微思考后，再一次完整表达算法：先算个位得到几个一，再算十位得到几个十，再算百位得到几个百，最后全部合起来。

以上练习，笔者用三道计算题引导学生完整表达算法，让学生对原本零碎的计算方法建立起联系。一节课，不应只局限于本节课、本单元的知识，更应让学生懂得建立以前、现在、未来知识间的纵向联系，揭示乘法计算的本质。这样的教学，学生学会举一反三，眼光放得更远，也培养了终身学习的能力。

三、拓展练习串线成网，意义建联中构筑知识体系

深度学习应是教师教会学生透过表面和浅层的现象，看到更深层次的规律，以寻求数学本质，让数学越学越简单。四则运算，即加、减、乘、除各有其不同运算算理，在二年级学习“表内乘除法”时，加与乘、减与除之间的联系进行了第一次沟通，学生初步感知四种运算两两间的连接点。而加、减、乘、除这四者在计算时，其算法又有何联系呢？课堂上，笔者借助拓展环节，引导学生探究分析它们各自在计算中每一步的意义，发现其本质是一样的，构筑完整的计算体系图。

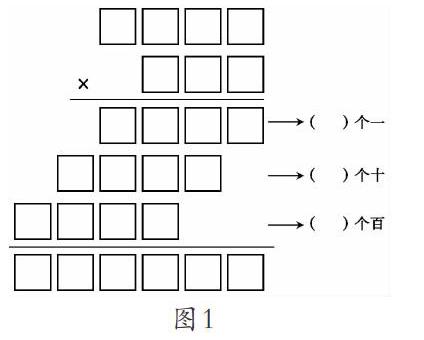
在拓展练习中，笔者借助课件展示方框图（图2），并引导学生想一想：整数乘法计算有“先分后合”的原理，加法呢，减法呢，除法呢？

有学生观察后回答：“加法，先分开算，个位得到几个一，十位得到几个十，百位得到几个百，再全部合起来。”随后，又有学生迫不及待地说：“减法，也是先分开算，得到几个一、几个十、几个百，再全部合起来。”笔者追问：“除法呢？”学生面面相觑，有个学生低声说：“除法是从最高位算起的。”笔者接着说：“咱们一起来看一下，除法从高位起，先算百位上除以一个数得到什么，接着呢？”学生回答道：“再算十位上除以一个数得到几个十，个位上除以一个数得到几个一，最后把百位、十位、个位上的数全部合起来。”此时教室里响起热烈的掌声。笔者随之引导学生看看四个列式，看有什么发现。学生讨论后得出：加、减、乘、除计算写法不同，但本质是统一的，都是先分开算，得到几个一、几个十、几个百，最后全部合起来。笔者再引导学生比较：“哪种运算比较特殊一点？”學生发现：“除法，得从高位算起。”笔者最后总结：“瞧，四则运算原来有如此密切的联系，它们的本质是相同的。有人总结说‘计算计算，就是记一记、算一算，一共有多少个计数单位，有道理吧！”

在这样逐步递进、层层深入的交流中，教师带领学生深入理解四则运算的意义，进行一一剖析，通过对比发现，形成完整的四则运算知识体系，揭示数学本质，让书本越学越薄。

总之，深度学习涉及学生的多层次、多感官和多维度思考，是一种系统性的学习，是提高学生数学核心素养和推进教育变革的有效策略。教师应不断对自身的教学加以思考，从学生的知识结构出发，从而让深度学习真正发生。

（作者单位：福建省永春县第三实验小学）