课程视野下的整体思维建构
胡倩云

【摘要】在新型冠状病毒肺炎疫情期间,教师给学生提供了形式多样、内容丰富的课程资源包。但在这些资源包里,知识点大多是独立且分散的,学生难以对不同知识进行整体的把握。本文以苏教版小学《数学》四年级(下册)《常见的数量关系》一课为例,采用解读教材、把握实质、整体视角、紧扣核心等策略帮助学生理解教材,提升思维水平。
【关键词】整体思维 数量关系 课程
整体思维又称系统思维,它认为整体是由各个局部按照一定的秩序组织起来的,要求以整体和全面的视角把握对象。布鲁纳认为,学习的实质是一个人把同类事物联系起来,并把它们组织成赋予了一定意义的结构,亦即学习者主动通过感知、领会和推理,促进类目及编码系统的形成。布鲁纳的观点从认知结构的角度阐明了整体思维是认识世界的有效方式。
去年在新型冠状病毒肺炎疫情的影响下,复学前基础教育教学采用了线上教学的形式。线上教学时,教师给学生提供了形式多样、内容丰富的课程资源包。但在这些资源包里,知识点大多是独立且分散的,学生难以对不同知识进行整体的把握。复学后,学校教学也面临许多挑战,如:学生的两极分化更为严重;学生一直在进行机械式学习,对知识的理解不透彻;教师的教学时间相对更少,教学压力变大。面对这种情况,如何进行整体思维教学,建立知识之间的本质联系呢?下面笔者以三组数量关系教学为例,谈谈自己的思考与实践。
一、解读教材,把握实质
常见的数量关系是人们对客观世界中纷繁复杂的数量关系的概括和总结,具有高度的抽象性和普遍适用性。学生在平时的学习中已经积累了丰富的数量关系知识,在整数四则运算教学的结束阶段,教师安排常见数量关系的学习内容,引导学生对已经掌握的数量关系进行抽象与概括,进而从更抽象的层面上去理解所学知识,既是培养学生分析和解决问题能力、提高数学思维水平的需要,也是学生进一步学习和生活的需要。
教学“单价、数量、总价”的关系时,考虑到学生在日常生活中经常会遇到购物的实际情况,对“单价、数量、总价”这一组数量关系较为熟悉,所以教材首先安排“单价、数量和总价”这一组关系。教师先引导学生说出每种商品的单价和数量,再试着用复合单位的形式表示练习本的单价,联系表格让学生思考“总价与单价、数量之间有什么关系”,进而概括得出“总价=单价×数量”,进一步思考怎样根据总价和单价求数量,或是根据总价和数量求单价,从而全面认识总价、单价、数量三者之间的关系。从学生熟悉的生活实例出发,引导学生经历从具体到抽象的学习过程,并在这一过程中获得对常见数量关系的认识与理解,初步积累抽象与概括的活动经验,发展数学思维能力。
在教学“速度、路程、时间”的关系时,由于学生对“速度、路程”等概念相对比较陌生,教学时,教师要结合实际问题中的数量关系,引导学生经历从具体到抽象的学习过程。那么,在教学时,如何进行整体思维培养,在归纳总结数量关系的同时建立起认知结构呢?
二、整体视角,紧扣核心
教材是众多学者思想的精华,是教学的重要课程资源,而学生永远是课堂学习的主体,如何创造性使用教材,从学生的实际需要出发,从儿童的视角再读知识的发生和发展过程,是非常必要的。在教学“速度、时间、路程”这一数量关系时,考虑到“速度”这一概念比较抽象,有教师会用很多时间来帮助学生理解“速度”。也有教师通过组织学生观看《动物世界》中猎豹追赶羚羊的视频情境来引入抽象的“速度”概念,让学生加深对“速度”的理解。
毋庸置疑,“速度”这一概念对学生来说,的确是抽象的、难以理解的,除了单纯地加深学生对“速度”的印象之外,教师还可以把“单价”和“速度”进行纵向联系,进而沟通总结这两组数量之间的关系,通过“串点成线”的方式,让学生感受到数学知识是前后联系的,从而建立整体认知结构。
1.理清概念,建立模型。
小阳:我买钢笔总共用去15元;小红:我买钢笔总共用去20元。
师:买钢笔共用去多少元,称为总价。小阳买钢笔这句话可以表示成“小阳买钢笔的总价是15元”,小红的这句话可以怎样表示?
师:两个小朋友,谁买的钢笔便宜些呢?
生1:小阳买的钢笔便宜些,因为小阳用的钱少。
生2:也可能是小红买的鋼笔便宜些,因为不知道他们各买了几支钢笔。
师:也就是说,要想知道谁买的东西便宜,不能只看总价,还要看买了几支,也就是数量。我们再来看看他们各买了几支。
教师出示课件:小阳买了3支钢笔,小红买了5支钢笔。
师:现在你知道谁买的钢笔便宜了吗?你是怎么想的?
生3:因为15÷3=5(元),20÷5=4(元),4比5小,所以小红买的钢笔更便宜。
师:说得真好!你知道这里的5元、4元分别表示什么吗?
生:表示一支钢笔的钱,也就是钢笔的单价。
师:买钢笔一共用的钱叫总价,买一支钢笔用的钱叫单价。小阳买钢笔的单价是5元,小红买钢笔的单价是4元。
师:怎么求物品的单价?
生:单价=总价÷数量。
师:数量比较好理解,单价和总价有些不太好区分,你有什么好方法吗?
生:总价是一共花的钱,单价是买一支钢笔的钱。
师:我们看看不同地区苹果的单价,它们的单价一样吗?
10元/个 10元/盒 10元/千克
生:它们的单价不一样,虽然都是10元,但是买到的数量是不一样的。
师:看来,要说清楚一件商品的单价,仅仅说清多少钱还是不够的,还要讲清楚计量的方式。
师:10元/千克,这是什么意思?这个单位和我们之前学过的单位有什么不同?
生:中间多了一条斜线。
师:是的,这里的元是总价的单位,千克是数量的单位。中间的“/”相当于“÷”。
师:这个单位有点特别,从中我们可以看出总价、数量和单价之间的关系。
师:怎么读呢?
生:10元每千克。
师:像这样的单位叫复合单位。这里的10元是每千克苹果的价钱。
设计意图:教学活动必须建立在学生已有经验的基础之上,此教学环节教师采用了学生常见的购物情境。把握学生知识的生长点,需要结合具体情境理解让学生对“单价”“总价”的概念加以区分和理解。通过复合单位和数量关系的对比,巧妙地突破了复合单位的难点,也进一步促进了学生对单价概念的理解,为学生后续学习提供了良好的思维支撑。
2.类比提升,深化思考。
师:老师开车从淮安到常州,速度是每小时100千米,时间3小时。
师:谁能试着解释一下“速度”的含义?
生:在这里速度是指每小时走的路程。
师:请你联系单价的表示方法想一想,在这里速度还可以怎么表示?
生1:可以表示为100千米/时。
生2:还可以表示成100千米/时,这样更简单。
师:老师开车从淮安到常州,速度是100千米/时, 时间是3小时,行驶的路程是多少千米?
生:100×3=300(千米)。
师:摩托车的速度50 千米/时,如果老师开摩托车要几小时?
生:300÷50=6(小时)。
师:现在开通了动车,如果动车的速度是300千米/时 ,坐动车从淮安到常州需要几小时呢?
生:300÷300=1(小时)。
师:你们都是怎么求出时间的?
生:路程÷速度=时间。
师:那如果要求速度呢?
生:路程÷时间=速度。
师:仔细观察下面這张表格,你还有什么发现?
生1:我发现:速度×时间=路程。
生2:我发现:路程相同,速度不同,所用的时间也不同。
生3:我发现:路程相同,速度越快,所用的时间越少;速度越慢,所用的时间越长。
师:是的,速度在变的时候,所用的时间也在变,但是什么一直都没有变?
生1:路程没有变。
生2:“路程=速度×时间”这个数量关系式没有变。
设计意图:与“单价”相比,“速度”这一概念比较抽象,像这样借助单价的学习经验来帮助学生理解速度,将模糊的快慢感知转化为单位时间内的路程的描述,有利于学生主动构建速度的概念。进而根据“速度×时间=路程”,求出总路程;再根据“路程÷速度=时间”,求出时间;灵活解决速度、时间、路程有关的实际问题,提高学生应用所学知识解决问题的能力。在分析图表中,学生进一步分析发现路程不变,速度越快,所用的时间越少;速度越慢,所用的时间越长。感受速度、时间、路程三者是有联系的。
3.对比分析,沟通联系。
师: 刚才提到的“单价×数量=总价”“速度×时间=路程”这两个数量关系,它们有什么联系呢?你能用一幅简单的示意图表示这种联系吗?
师:你能解释一下这个图的意思吗?
生1:我们可以把上面的两个数量关系都想成“1份的数量×份数=总数”这一个数量关系。
生2:速度就是1小时或者1分钟走了多远,单价是1支或者1本的价钱,所以这两个数量可以用图中的一小段表示,而时间和数量可以看成是几段,就是几份。最后的结果就是总数,也就是路程或者总价。
师:也就是说在单价、数量、总价中,速度和哪个比较像?时间和哪个比较像?路程呢?
生1:速度和单价比较像。单价是一件物品的价钱,速度是一小时或一分钟走的路程。
生2:而且它们都要用两个单位才能说清楚。
生3:时间和数量比较像,路程和总价比较像。
师:噢,原来它们之间还有着这样的本质联系呢,在不同的情境中,把这些数量换成不同的称呼和数据,就可以变成不同的问题,但本质是一样的。看来数学的知识不是独立的,而是有着紧密的联系啊!
设计意图:通过画线段图,让学生直观地感受“速度、时间、路程”这一组数量和“单价、数量、总价”这一组数量之间的关系,从直观感知到理性归纳,提升课程整合意识,构建整体思维,不断提高解决问题的能力。
4.拓展延伸,积累经验。
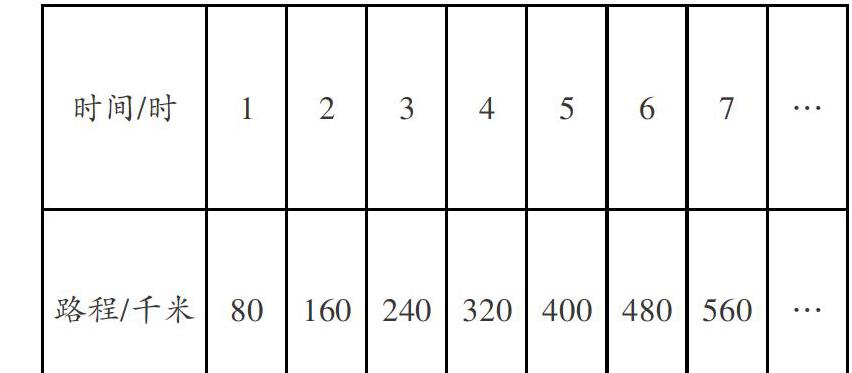
一辆汽车在公路上行驶,行驶的时间和路程如下表。
师:仔细观察上表中的数据,你又有什么发现?
生1:行驶的速度不变,都是80千米/时。
生2:速度不变时,行驶的时间越长,行驶的路程就越多;时间越短,路程就越少。
设计意图:以整体思维的方式展开教学,让学生初步感受从变化的角度分析数量关系的方法,体会数量之间总是相互依存、互相影响的。通过这样的教学设计,深化了学生对这几个量之间关系的理解,体现了数学知识发生、发展的内在逻辑,努力为学生的后续学习提供学习经验和方法。
(作者单位:江苏省常州市华润小学)

