驱动马达定向运动的随机动力学模型

杨紫贝，邱 星，陈巧妮，王海燕

(北京师范大学 物理学系，北京 100875)

分子马达既具有酶的活性又具有运动活性，能够将三磷酸腺苷(ATP)水解产生的化学能转化为机械能，负担着包括肌肉收缩、细胞活动和细胞内物质输运等几乎所有的生物活性运动[1]．为理解分子马达定向运动的物理机制，国内外学者从理论和实验方面开展深入研究[2-6]，其中基于费恩曼棘轮思想的“布朗马达”是重要的理论模型之一[7]．布朗马达是将分子马达抽象为处于非对称周期势中的布朗粒子,在热噪声和非平衡涨落的条件下，能产生定向运动的物理模型．其中，非对称周期势表示分子马达与轨道的相互作用,这一作用导致布朗马达系统的对称性破缺；热噪声反映环境对分子马达的影响,引起布朗粒子的扩散运动；非平衡涨落是由ATP水解产生的，为驱动马达定向运动提供需要的能量，使系统偏离热力学平衡状态．研究表明，布朗马达产生定向运动的物理本质在于：非对称周期势和非平衡涨落的共同作用，使得一定温度下的布朗粒子向前和向后扩散的几率不同, 从而产生定向运动．

Visscher和Block等人[8]在单分子实验中发现驱动马达以8.2nm左右的固定步长定向行走,同时也具有一定的随机性，驱动马达的速度随负载力的增加而减小，马达每行走1步催化水解1个ATP分子,说明驱动马达的机械运动和化学反应是紧密耦合的。因此，在本文中我们在非对称周期势中考虑驱动马达的机械化学耦合，基于布朗马达的工作原理，利用MATLAB数值模拟驱动马达在一定实验条件下的运动特征．本研究可以为统计物理教学提供一个有趣的实例，同时为大学生利用物理规律解决实际问题提供可以借鉴的思路和方法[9]．

1 机械化学耦合模型

1.1 ATP水解反应产生的自由能与活化能势垒E

单分子生化实验表明驱动马达每行走1步催化水解1个ATP分子，ATP水解为ADP和磷酸根Pi的化学反应方程式为[8]

(1)

水解产生自由能为

(2)

其中，ΔG0是水解平衡值，ΔG和ΔG0的单位均为(pN·nm)，[…]表示反应物和产物的浓度，实验温度为25℃(kBT～4.1pN·nm)条件下，ΔG0=55 pN·nm为一个常数，并保证溶液中[ADP]和[Pi]的浓度值为0.01μM·L-1．实验测量表明，驱动马达能够利用一半的水解自由能来产生定向运动，我们将这部分自由能称为有效自由能ΔGu，单位为(pN·nm)，有效自由能ΔGu的表达式为

ΔGu=(27.5+2.05ln(104[ATP])) pN·nm

(3)

化学反应速率常数与[ATP]之间关系的Michaelis-Menten表达式[8]：

(4)

其中，KM是米氏常数，kmax是高浓度ATP下的水解反应速率常数．化学反应的实质是旧键的断裂和新键的形成，ATP水解首先需要打开ATP分子中的共价磷酸键，这一过程需要吸收热涨落提供的能量来克服活化能势垒E．Kramers 理论给出了这个过程的反应速率常数与温度的关系[10]:

(5)

其中，k0是阿伦尼乌斯常数．那么式(4)中的kmax可以写为

(6)

其中，E0=1 pN·nm．结合式(4)、(5)、(6), 可以得到活化能势垒E与[ATP]的关系式:

(7)

1.2 非对称周期势

由于驱动马达的机械化学耦合，当行走中的驱动马达处于ATP水解反应的不同化学状态时，驱动马达与轨道相互作用势也不同，因此，我们引入中包含ATP水解反应中的活化能势垒E以及有效自由能ΔGu的非对称周期势V(x)，如图1所示．

(8)

图1 驱动马达与轨道相互作用的非对称周期势(m=0,1)

周期势以步长l0为周期，参数(1-α)表示化学反应对应的空间步长比例，即在((1-α)l0) 的步长空间里，驱动蛋白吸收热噪声提供的能量来克服活化势E，并发生化学反应, 这个过程驱动马达的速率几乎为零，因此我们称之为等待态．只有成功克服势垒的驱动马达才能产生定向运动，进入行走状态．由此可见，驱动马达与轨道相互作用的非对称周期势V(x)反映了驱动马达行走中的机械化学耦合．

1.3 驱动马达的运动模型

用过阻尼朗之万方程描述驱动马达在非对称周期势V(x)中的运动[11]：

(9)

<ξ(t)>=0，

<ξ(t)ξ(t′)>=2Pδ(t-t′)，

P=λkBT

(10)

2 结果与讨论

(11)

其中

(12)

我们选择与实验中相同参数[8]：λ=8.00×10-3pNs·nm-1、α=7.30×10-1、KM=1.02×103μM·L-1、[ATP]=2.00×103μM·L-1、F=6.50 pN、l0=8.20 nm.借助MATLAB模拟了1000个粒子的运动．首先我们得到驱动马达的位移随时间的变化图像，如图2(a)和(b)所示．

从图2(a)中能看到呈阶梯状的位移轨迹，为了仔细观察驱动马达的运动情况，我们将某一段位移-时间图像放大后得到图2(b)，可以清晰看出驱动马达的运动步长接近8.2 nm(图中标出的两组数据对应的Y轴坐标差值约为步长周期的2倍)．驱动马达每行进一步都会停留一段时间，如图2(b)中对应的平台所示，可以理解为这段时间是驱动马达吸收热噪声提供的能量来克服活化势E的过程，对应于非对称周期势(图1)中((1-α)l0) 部分的等待态．由于热涨落在这个过程中的起主导作用，马达运动具有一定的随机性．同时，可以观察到图2(b)中相邻平台之间的阶梯，为驱动马达将ATP水解产生的能量转化为机械能的过程，这一阶段驱动马达克服活化势垒后，产生了定向运动，对应非对称周期势(图1)中(αl0) 部分的行走态．模型结果表明驱动马达的运动是由等待态和行走态组成的,与Visscher和Block实验中观察到的结果吻合[8]．为进一步研究驱动马达的运动我们计算了驱动马达的速率，如图3(a)和图3(b)所示．

单个驱动马达x-t图

图示(a)的放大图2

在图3(a)中，单个驱动马达的速率随时间的变化体现了驱动马达具有行走和等待的“两态”，速率大小的涨落表明运动具有随机性．在图3(b)中，我们分别计算n个驱动马达的平均速率，即用单个驱动马达的位移除以时间，从而得到n个不同驱动马达的平均速率为150 nm/s左右，对比发现模型得到驱动马达的运动速率与实验中观察的结果一致[8]，同时还可以观察到不同驱动马达的平均速率也存在一定的随机涨落．

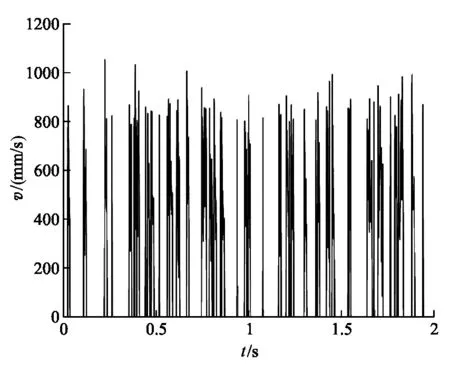
单个驱动马达v-t图

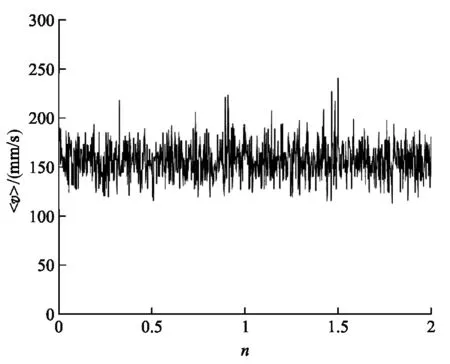
n个不同驱动马达的平均速率图图3

为了研究负载力对驱动马达运动的影响，考虑驱动马达运动的随机性，我们在不同负载力下，先分别计算n个驱动马达运动速度的时间平均，然后计算n个驱动马达运动速度的系综平均随负载力的变化图像，如图4所示．

从图4中，可以看出驱动马达运动速度的系综平均值随负载力F的增大而逐渐减小，同样与实验观察的结果[8]相吻合．

图4 驱动马达运动的系综平均速度与F关系图

3 结论

本文以非平衡态随机动力学方程和驱动马达运动的相关生化原理为基础，在非对称周期势中体现驱动马达运动过程中的机械化学耦合，并数值模拟得到相关图像．将模拟图像与实验结果进行对比，验证了驱动马达的运动具有定向性、固定步长和一定随机性的特点，表明所用模型的合理性．