低功率激光热透镜效应的模拟及研究
郭政鑫,高绮妮,范紫萍,陈清楠,郑博为,彭 力,2
(1.华南师范大学 物理与电信工程学院,广东 广州 510006;2.华南师大(清远)科技创新研究院有限公司,广东 清远 511517)
热透镜效应常见于激光照射到晶体或有机溶液上,已经成为物质微弱吸收测定的有力工具,热透镜焦距则是衡量热透镜效应的一个重要参数. 探究和认识热透镜现象也是本科生融会贯通光学与热学知识的有效途径. 然而,目前对于热透镜效应的研究主要集中在对于谐振腔介质热透镜效应的分析上,如对Nd:YAG晶体热应力的测算[1],磁流体光学特性研究[2]等. 以上工作研究的对象大都是用于工业的高功率激光器,缺少从实验教学的需求出发,对于热透镜焦距影响因素的定量研究,且验证理论对于实验条件的要求较为严苛,不适合直接引入到本科课程教学之中. 因此,探究并总结低功率激光器在介质中的光热特性可为普物实验教学提供实用的理论解释. 现代有限单元法结合有限差分法与解析变分法的优势,可高效准确地获得微分方程的数值解,本文将介绍对于低功率激光器的有限元模拟方法,展示介质内部温度场分布,从保证实验可行性的角度出发,研究低功率激光器热透镜焦距与介质厚度、吸收系数以及激光功率等参数的关系,与实验结果对比符合良好.
1 理论介绍
1.1 热透镜效应的定性分析
高斯型激光的光强表达如下式(1),当其透射到有机溶液时,溶液中的有机分子吸收了光子而被激发,再以非辐射的弛豫方式回到基态,把吸收的全部光能以热的形式释放出来[3]. 这种加热作用导致了在受辐射的溶液局部区域中产生了呈径向对称的温度分布[4].
I(r)=I0e-r2/w2
(1)
酱油介质的折射率函数与温度呈负相关[5]. 中心温度高,四周温度低的温度场,使得在酱油中在光束轴心处的光程较边缘短一些(见式(2)),对光束的作用等效于凹透镜.
ΔD(x,y)=knl(x,y)
(2)
高斯光束经凸透镜汇聚形成焦点,当酱油薄片放在光斑焦点后,对高斯光束起发散作用,远场高斯光斑增大.
1.2 激光照射下介质内热场分布
我们模拟的系统可由图1所示,高斯激光经过凸透镜会聚在装有介质的样品薄片中,主要对介质内部热场分布进行模拟,借此探究热透镜效应.
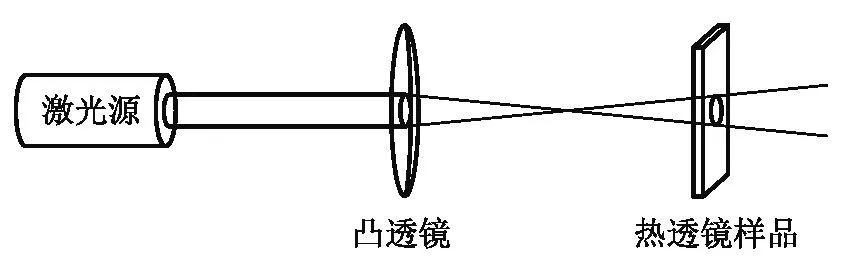
图1 系统示意图
根据热学分析,稳定后介质中的温度分布满足稳态热传导方程[6],由于激光具有轴对称性,故可以将其化为二维形式:
(3)
其中,T为温度,r为与光束中心在径向上的距离,z为光束传播方向上的距离,λ为介质的热传导系数.q=q(r,z)为介质中的热源分布,该分布受到激光光强分布影响,高斯光束光强分布可表示为
(4)
以此我们可以写出激光加热介质时,介质内部的产热分布
(5)
其中Pin为激光功率,a和η分别为介质的吸收系数以及热转化率,l为介质厚度.ω(z)为距激光束腰距离为z处的光束半径,其表达式为
(6)
其中ω0为光腰处半径,另外,温度场还满足以下边界条件:
(7)
(8)
其中,h1和h2分别是空气和酱油的对流换热系数,Ta和Tb分别是酱油与空气的初始温度.
1.3 热透镜焦距的计算
介质不同径向距离处与中心的光程差可以表示为[7,8]
(9)
其中,n为介质的折射率分布,它与温度分布有关,表达式为[9]
(10)
T0为介质所处的室温,n0为室温下的介质折射率,β为膨胀系数. 从几何光学的角度来说,光程差又可以表示为
(11)
其中f为热透镜的等效焦距,联立式(10)、(11)就可以得到根据温度分布以及折射率分布求解热透镜焦距的表达式:
(12)
由于最终产生的等效透镜不是完美的球透镜,不同径向位置会将光汇聚在不同焦距处(数值解析都可以证明),我们将取焦距的平均值作为有效热透镜焦距,后文都直接简称为热透镜焦距.
1.4 有限元法求解温度场
对于求解微分方程,古典近似计算分为有限差分法与解析变分法两大门类[10],有限差分法的特点是引入了离散化的思想,而解析变分法是引入试探函数并对整个区域积分的方法. 而现代有限单元法则结合两者的优势,能够高效准确地获得微分方程的数值解,本文就是根据文献[10]中的方法,在软件中编写有限元法程序求解1.2中热传导方程.
为了更加清晰地说明,将列出数值模型中所有的参数,如表1所示.

表1 物理量和符号列表
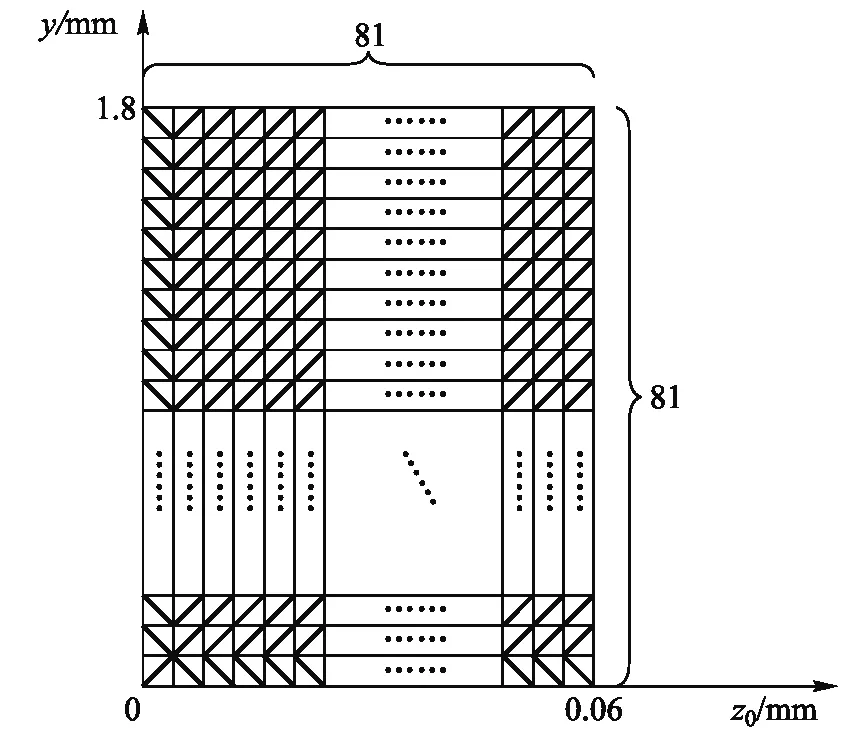
图2 求解区域的选择与离散化
为了方便处理,这里将温度场求解区域设为过光束圆形直径的矩形截面,矩形的长和宽分别是光束的光斑直径以及介质的厚度. 根据有限元法的要求,先将求解区域的长和宽分别81等分并记录每一个节点的坐标,再按照规则将每个小矩形单元划分成两个三角形单元,如图2所示.
有限元法求解温度场分布的核心是求解(13)式所示的线性代数方程组,其中系数矩阵[K]称为温度刚度矩阵,[N]称为非稳态变温矩阵,矢量{p}是等式右端组成的列向量,而矢量{T}便是由我们要求解的各个节点的温度值组成. 由于我们只关心温度场稳态时的温度分布,故[N]项可以不用考虑.
(13)
对于第三类边界条件的温度场,根据有限元法理论有如下关系,i,j,m分别代表每个三角形单元的3个节点标号,热源分布q可以通过将节点坐标代入式(5)获得:

kij=kji=φ(bibj+cicj),
kim=kmi=φ(bibm+cmci),
kjm=kmj=φ(bjbm+cjcm)+hsi/6,
(14)
另外,bi,j,m和ci,j,m是也是节点坐标的函数,满足以下关系:
bi=yj-ym,ci=xm-xj,
bj=ym-yi,cj=xi-xm,
bm=yi-yj,cm=xj-xi
(15)
确定了每个单元的情况就可以合成温度场的温度刚度矩阵[K]以及矢量{p},通过矩阵除法运算求解出温度场矢量{T}.
2 仿真模拟及实验结果分析
2.1 介质中的温度场分布
建立好模型后,将:Pin=5.0×10-3W,α=1.0 m-1,η=0.50,T0=300 K,λ=0.30W/(m·K),ω0=1.0×10-4m,h=200W/(m·K),r=0.90×10-3m,z0=6.0×10-4m,代入模型可解得介质中的温度分布,如下图所示.

图3 介质中的温度分布
从图中可以看出,低功率激光中心照射区域介质的温度最高,越靠近光束边缘或者越深入介质温度越低. 获得完整的温度场信息之后,接下来就可以利用温度分布来求解等效热透镜焦距.
2.2 激光功率对热透镜焦距的影响
求解出介质内的温度分布,可以利用式(10)、(12)计算介质的等效热透镜焦距. 保持其他参数不变(同2.1),探究不同激光功率Pin对热透镜效应的影响. 仿真和实验都设定将介质放置在面积固定激光光腰处,又考虑到实验室直接可以控制的是激光功率,故直接采用激光功率为自变量进行研究,为了保证实验的可操作性以及安全性,我们将最大功率定为10 mW,结果如下.
从图4可以看到,随着功率增大,介质轴线的整体温度逐渐升高,图5、6中也可以从径向截面看,随着功率增大,介质整体温度升高,介质的轴线到两侧的温度梯度越来越大. 这导致折射率梯度也越来越大,等效热透镜焦距减小. 如图7所示,热透镜效应更加明显. 图8显示,100~110 mw下热透镜焦距变化平缓. 图7、8相比较,相同功率变化范围下低功率激光热透镜焦距的变化更明显,推荐选择10 mW 以下的激光器进行实验.
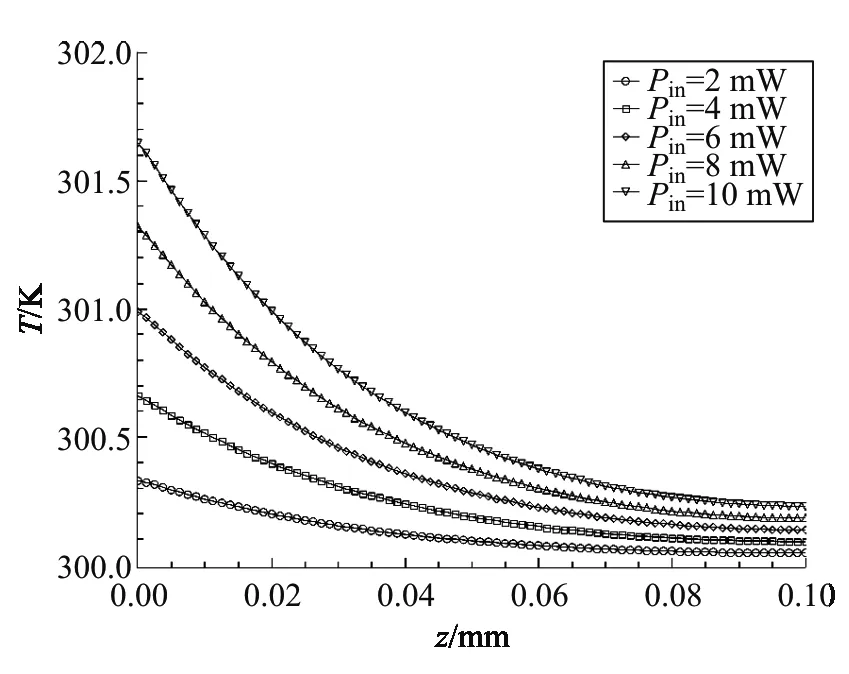
图4 不同功率下光束中轴线上介质的温度分布

图5 不同功率下介质中径向的的温度分布
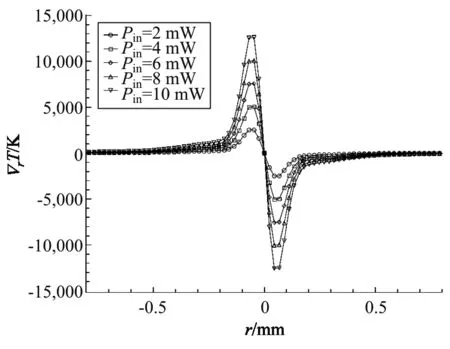
图6 不同功率下介质中径向的的温度梯度
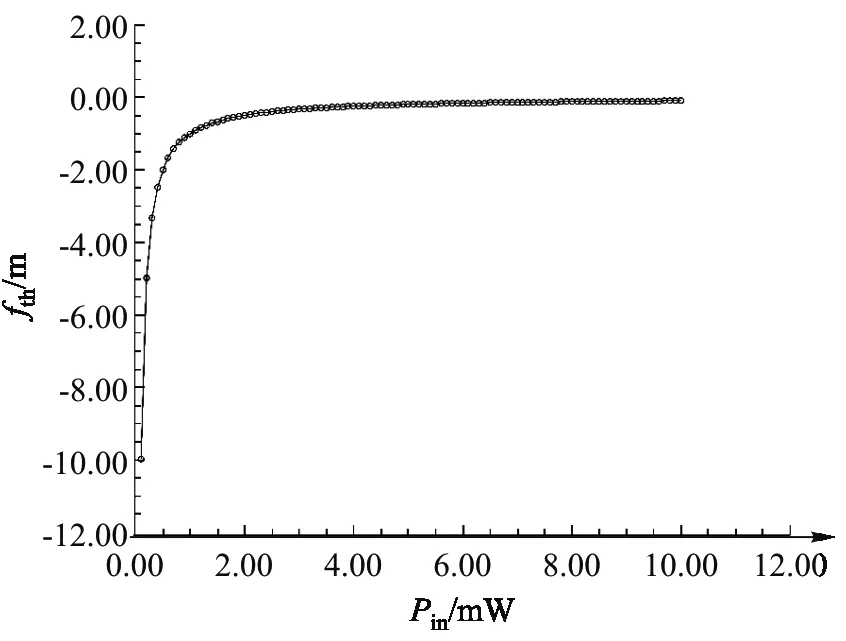
图7 不同功率热透镜焦距

图8 功率100~110mW下热透镜焦距变化参考
2.3 不同介质特性对热透镜焦距的影响
除了激光功率以外,介质的种类也是影响热透镜效应的关键因素之一. 我们选择不同介质,进行以下讨论.
2.3.1 吸收系数对热透镜焦距的影响
保持其他条件不变,取不同的吸收系数,以模拟不同的液体介质浓度对于热透镜焦距的影响,结果如图9所示.
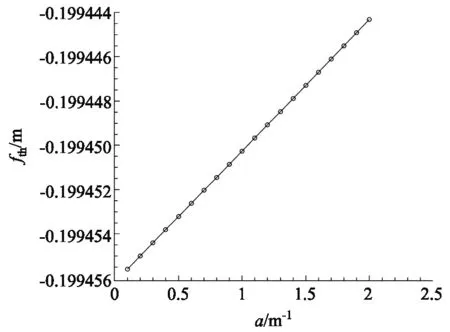
图9 热透镜焦距与热吸收率的关系
模拟结果显示,在低功率激光作用下,随着介质吸收率的升高,热透镜焦距绝对值呈现线性降低趋势.
2.3.2 厚度对热透镜焦距的影响
探究不同介质厚度对于低功率激光热透镜效应的影响,同样保持其他条件不变,将从0.01 mm开始逐渐增加介质厚度,模拟出对应的热透镜焦距如图10. 另外需对厚度进行限制,因为模型难以考虑介质散射及吸收对热透镜效应的影响,不一定对厚的液体介质适用.
从结果中可以发现一个有趣的现象,介质厚度逐渐增加的过程中,热透镜焦距并没有呈现一个单调变化的趋势,而是在一个厚度处出现了一个极值. 从图10中极值点附近取三个厚度的介质,分别绘制光束中心线上的温度分布,如图11所示.
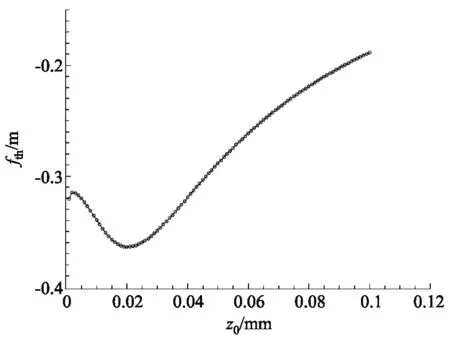
图10 热透镜焦距与厚度的关系
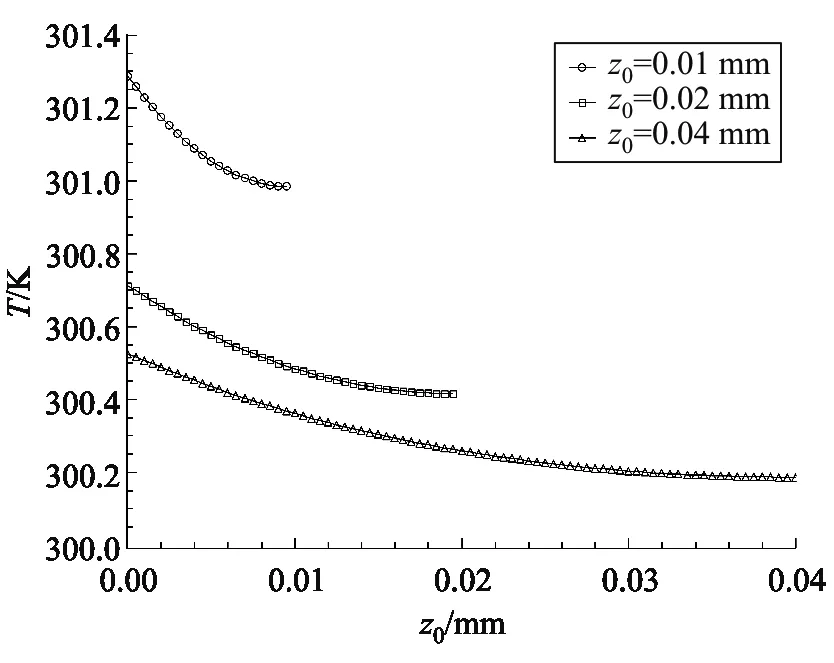
图11 不同厚度介质光束中轴线上的温度分布
可见厚度为0.01 mm的介质虽然比厚度为0.02 mm的介质与激光作用的距离短,但是由于厚度较小,介质可被激光充分加热,同时在边界散热较快,故具有更大的温度梯度,导致热透镜焦距绝对值更小. 而厚度超过0.02 mm的介质,虽然激光功率不足以充分加热整块介质,但随着厚度的增加,因等效热透镜的累计效应,热透镜焦距绝对值也会呈现减小趋势.
因此,若出现热透镜效应较不明显的情况,可以适当减小或者增加介质厚度. 但介质厚度不宜过厚,过厚的介质会对激光产生较强的吸收和散射,导致透过介质的光线很弱,不易观察和测量.
3 实验验证
为了验证仿真结果的可靠性,设计并搭建可以测量介质等效热透镜实验平台,使用不同浓度及厚度的介质进行验证实验.
3.1 热透镜焦距的测量
实验过程为,首先利用刀口法[11]测量激光透射介质后在光屏留下的光斑半径,再测量各光学器件之间的距离,利用光学矩阵法[12]就可以根据以上参数计算出热透镜的等效焦距. 实验流程如图12所示.
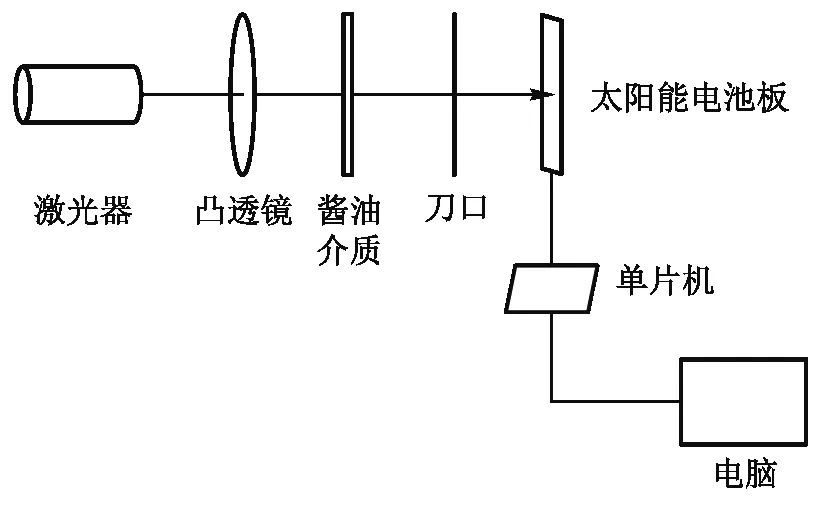
图12 实验装置示意图
3.2 介质参数的控制
为了能够验证热透镜焦距与介质热吸收率以及厚度的关系,制作不同浓度以及厚度的介质样品. 容纳介质的容器是由两片薄玻片间夹U型薄膜制成,介质选用商业酱油[12],如图13所示. 调节介质的浓度便可调控热吸收率,调控U型薄膜的层数便可控制介质厚度.

图13 不同参数的介质样品
3.3 实验结果
3.3.1 热吸收率对热透镜焦距的影响
采用一组等浓度梯度变化的介质溶液进行实验,得到热透镜焦距变化如图14, 其中介质厚度均为0.1 mm,各组介质占与纯水混合溶液的浓度分别为20%~100%. 实验结果大致与理论分析符合,焦距呈线性变化. 由于实验时容器玻片会对入射激光产生一定反射,损失部分能量,故热透镜焦距会与理论值存在一定的差距.
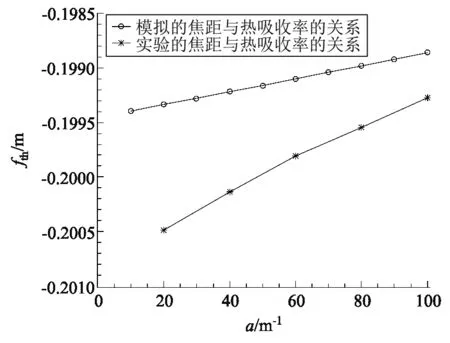
图14 热透镜焦距与热吸收率的关系
3.3.2 厚度对热透镜焦距的影响
取介质浓度均为100%,制作厚度分别为0.01、0.02、0.03、0.05、0.07 mm的介质样品进行多次测量热透镜焦距,结果与模拟值趋势大致相同,误差同样主要来自玻片对光束的反射.

图15 热透镜焦距与厚度的关系
3.4 研究结论
根据以上讨论,对于搭建低功率激光热透镜实验系统,可以给出一些建议. 首先在激光功率的选择方面,在保证安全范围内尽量选择更大功率,建议选用10 mW以下的低功率激光器. 在介质选择上,选择热吸收系数较高的介质会有更好的效果,在热透镜效应不明显时可适当增加介质厚度. 目前已知在低功率激光热透镜特性良好的介质有聚吡咯甲烯-聚乙烯醇复合材料[5]、镍合金薄膜[13],2-(5-溴-2-吡啶偶氮)-5-二甲氨基苯胺[14]等.
4 总结
本文介绍了利用有限元法模拟低功率激光器热透镜效应的方法,并且利用该方法获得了介质内的温度场分布. 除此之外,本文还探讨了介质热吸收率、厚度以及激光功率对于低功率激光器热透镜效应的影响,得出了热透镜焦距随激光功率增加绝对值减小,随着介质热吸收率上升绝对值减小,不随介质厚度变化而单调变化的结论,实验与模拟符合良好. 为采用不同激光器以及介质进行实验教学设计提供了理论参考.

