从简单模型入手探究陀螺仪在磁场中的减速问题
冯 鑫,范弘杰,程玉锟,赵 伟,陶小平,浦其荣,赵 霞,张增明
(中国科学技术大学 物理学院,安徽 合肥 230026)
近年来基于IYPT(International Young Physicists’ Tournament)题目的中国大学生物理学术竞赛活动在国内高校中开展的越来越广泛.这些具有很强开放性和可探索性的题目每年吸引了很多同学投入到相关学习和研究工作中,激发了同学们学习物理知识的热情,通过开展相关的教学和比赛活动有效提升了高校普通物理的教学质量.
2019年的IYPT题目中的第12题是一道关于磁致减速的问题. 一个由非铁磁性的导电材料制成的旋转的陀螺仪,被置于磁场中时会减速,要求研究相关参数对于减速的影响.
对于这个磁场中导体材料陀螺的减速问题可以用电磁学知识来初步定性分析,导电材料在磁场中运动时切割磁感线会产生动生电动势,产生的感应电流在磁场中会受到安培力,安培力矩作为阻碍陀螺仪旋转的阻力矩会导致陀螺减速.
一般磁场下陀螺仪的减速问题可以用麦克斯韦方程组求解,但过程较为复杂,也难以设计实验方案进行可重复性的定量验证. 本文以磁场中的无限长导体圆柱模型为基础,分析了陀螺仪转轴与磁场方向间不同角度下磁场导致陀螺仪减速的机理,得到了该模型下电磁阻力矩的近似表达式,并进行了量纲分析. 实验上为了能相对直接评估电磁阻力矩的大小,将力学量测量转换为电动机驱动电流测量,以直流永磁电动机驱动陀螺仪,验证了所建立模型的理论分析结果,归纳出陀螺仪减速过程中电磁阻力矩所满足的一般关系.
1 理论分析
减速问题中的磁场分布,在理论和实验中都只考虑均匀磁场情况,并不影响分析该问题的主要物理图像. 对于非均匀磁场,需要在分析中加入磁场梯度的影响[1],或者简单的选择一个特定位置的磁感应强度值[2],作为整个磁场代表值. 对于这个问题中磁场方向和陀螺仪转轴方向的相对取向,先考虑磁场方向垂直于转轴和平行于转轴两个特殊方向,再扩展考虑一般情况. 磁场方向垂直于转轴,即平行于转盘时,如图1所示,为分析方便选择区域为包含全部陀螺仪的匀强磁场;磁场方向平行于陀螺仪转轴时,若匀强磁场范围很大,包含整个陀螺仪,则显然旋转陀螺仪转盘中不会产生涡流[2],也就不会产生电磁致减速现象,这一点在实验上也可以明显观察到. 因此分析磁场方向平行于陀螺仪转轴时,假定陀螺仪圆盘上的一个小区域内施加轴向磁场.
1.1 磁场方向与陀螺转轴方向垂直
严格建模计算陀螺仪转子产生涡流的电磁阻力矩,需要根据麦克斯韦方程组,结合边界条件进行求解,过程相对复杂[2,3],考虑到陀螺仪可认为是绕定轴转动的圆盘,可以利用简单的导体圆柱模型分析电磁阻力矩的产生过程.
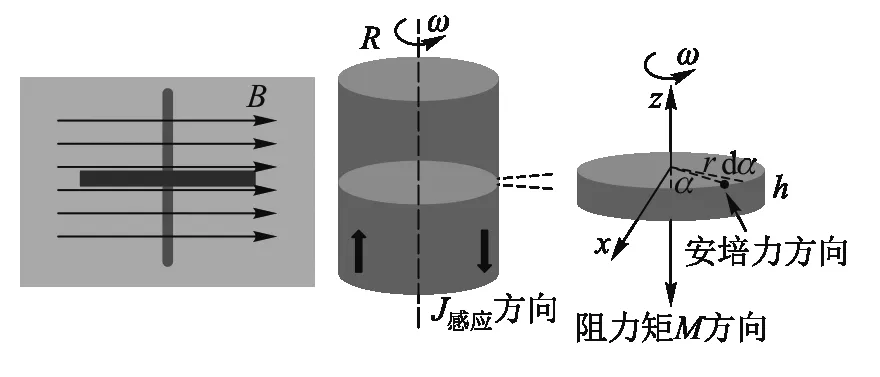
图1 磁场方向垂直转轴位形和无限长导体圆柱模型
如图1所示,若有一个无限长绕轴以角速度ω旋转的圆柱形导体,其半径为R,电导率为σ,密度为ρ,置于方向垂直于转轴的无限大匀强磁场中,磁感应强度为B. 该圆柱导体可看成距自身转轴距离不同的很多导体微元组成,如图1所示,这些导体微元切割磁感线会产生感应电流J感应. 截取该圆柱体上高度为Δh的一段圆盘进行分析,在忽略涡流产生的磁场的情况下,取与x轴夹角为α,角度为d的扇形区域,该扇形区域上距圆心r处的微元dr,其截面积为ds=rddr,如图1所示. 磁场方向水平指向右侧时,该微元所受安培力垂直纸面向外,即产生垂直向下的阻力矩,阻碍陀螺转动. 此时高度为h的微元产生的总动生电动势e可表示为
e=BΔhωrsinα
(1)
由微观欧姆定律,有
σG=j
(2)
其中G为单位长度导体切割磁感线产生感应电动势,j是电流密度. 上两式中e和G又显然满足:
e=ΔhG
(3)
联立上述式(1)-(3)可以得到
j=σBωrsinα
(4)
进而可以得出该导体棒在磁场中受到的安培力矩的表达式[6]为
dM=σωΔhB2r3(sinα)2drdα
(5)
对式(5)进行积分可以得到单位高度的导体圆柱的安培力矩表达式为
(6)
从式(6)可以看出,安培阻力矩与磁感应强度的二次方和角速度的一次方成正比. 同时考虑到虽然陀螺仪一般为厚度有限的圆盘,但由于圆盘与无限长圆柱具有相同的轴对称性,且产生减速效应的电流只是轴向电流,因而该问题中的陀螺仪圆盘受到的安培阻力矩与该理想模型应只相差一个和盘厚、半径有关的系数,若陀螺仪圆盘厚度为h,半径为R,则根据式(6)其所受的安培力矩可表示为
M垂直=λ(h,R)σhB2R4ω
(7)
对于磁场中的陀螺仪减速过程,除电磁阻力矩外,还应考虑空气阻力和摩擦等阻力的作用. 整体减速效应可以近似取到常值阻尼和与速度成一次关系的一次阻尼,忽略高次项,即

(8)
其中k为阻尼系数,对式(8)求解可得到角速度的减速过程公式为
(9)
式(9)说明,陀螺仪的角速度随时间满足指数衰减关系. 此外可以注意式(9)中的阻尼系数应包含非磁场产生的k0和磁场产生kB两部分,即
k=k0+kB
(10)
根据刚体转动定律,总阻力矩M,刚体转动惯量I,以及角加速度应满足如下关系:
(11)
式(11)中M其他为其他因素产生的阻力矩,圆盘的转动惯量I为
(12)
其中ρ为导体圆盘的密度,结合式(8)、(10)、(11)可得
M垂直=IkBω
(13)
将式(7)和(12)带入式(13),磁场的安培阻力矩产生的阻力系数为
(14)
1.2 磁场方向与陀螺转轴方向平行
当磁场方向平行于陀螺圆盘转轴时,如前所述可假定磁场只作用于转盘上一个小的矩形区域[3],如图2所示,该区域置于距圆盘中心充分远的位置,磁场垂直盘面. 稳定后在某一固定时刻,由于导体切割磁感线产生动生电动势,相当于在导体圆盘上“嵌入”一个“电池”,而流经该区域的电流将受安培力作用,这时圆盘受到一个阻碍其运动的安培力矩,因而减速. 对一般情况,可以将不规则、不均匀的磁场分割为多个小的这类均匀磁场,这时关于圆盘轴无旋转对称性的磁场也一定具有减速效应.
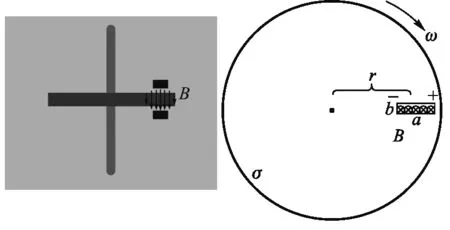
图2 磁场方向平行转轴位形和圆盘上矩形均匀磁场小区域模型
若磁场区域沿电流方向长为a,垂直电流方向宽为b,此区域距离盘心为r,圆盘电导率为σ,陀螺圆盘厚度为h. 某一时刻,圆盘的旋转角速度大小为ω,则该均匀磁场区域导体切割磁感线产生的动生电动势e为
e=Baωr
(15)
若此区域相对圆盘充分小,此时等效电池的内阻可以表示为
(16)
为得到感应电流需要计算外电阻,等效外电阻的求解需要算出整个盘面的电流分布,但若磁场位形确定时,等效外电阻阻值一定为一常量,记为R,则由欧姆定律得
I=ασBbhωr
(17)
式(17)中α是磁场位形和圆盘几何尺寸确定时的常数,其满足
(18)
于是此时安培力矩可以表示为
M平行=ασB2abhωr2
(19)
从式(19)可以看出,与磁场方向垂直转轴时的结果类似,此时安培阻力矩也与磁感应强度的二次方和角速度的一次方成正比.
1.3 直流电机转矩与阻力矩
为更方便的研究电磁阻力矩与磁场及角速度的相互依赖关系,实验中引入额定电压为6V的130式直流永磁电机辅助,利用其一定电流下的转矩来平衡电磁阻力矩,进而将力学量测量转换为电动机驱动电流测量. 一定转速范围内,直流电动机稳定时的输出转矩与其电枢电流强度平均值有非常好的线性关系[4,5],即
M=η(I-I0)
(20)
当直流电机驱动陀螺仪以稳定角速度转动时,应满足
MB+Mf=M
(21)
其中MB为电磁阻力矩,Mf为摩擦力阻力矩,结合式(10)可知Mf应满足
Mf=k0ω
(22)
由式(7)和式(20)—(22)可得,磁场方向垂直于陀螺仪转轴时,电机驱动电流和磁感应强度和角速度的依赖关系为
(23)
由式(19)-(22)可得,磁场方向平行于陀螺仪转轴时,电机驱动电流和磁感应强度和角速度的依赖关系为
(24)
1.4 量纲分析
在式(7)、(19)或式(23)、(24)中可以发现,电磁阻力矩与磁感应强度平方成正比,和角速度成正比. 对于这一点,从物理分析中的量纲分析方面也可以进行说明.
对于旋转陀螺仪在磁场中受到的磁力矩M,可能与外磁场磁感应强度B,旋转角速度ω,材料电导率σ,以及系统几何参量(不妨统一记为D)有关. 若假定长度、质量、时间、电流的量纲分别为L、M、T、I,则各物理量的量纲表示如下:
[B]=L0M1T-2I-1
(25)
[ω]=L0M0T-1I0
(26)
[σ]=L-3M-1T3I2
(27)
[D]=L1M0T0I0
(28)
若电磁力矩满足
M=λBαωβσγDδ
(29)
式(29)中λ为无量纲常数. 同时力矩M的量纲满足
[M]=L2M1T-2I0
(30)
即可解得
M=λB2ω1σ1D5
(31)
量纲分析的结果式(31)与式(7)、式(19)的结果一致,关于电磁阻力矩的推导结果可以认为是合理的.
1.5 磁场方向相对于陀螺仪转轴取向任意角度时
当磁场方向相对于陀螺仪转轴方向取向任意时,情况较为复杂,但可以在之前两种特殊情况基础上,对任意取向下的减速过程作粗略的讨论. 此时可令磁场方向始终为水平方向,陀螺仪转轴与竖直方向夹角为α.
磁场方向平行于陀螺仪转轴的部分可认为没有减速效应,故公式中只应包含垂直于转轴的减速效应,即cosα项. 同时陀螺仪自身与摩擦有关的一次阻尼系数也将发生变化,阻尼系数与作用力大小成正比,故公式应包含sinα和cosα项. 由于垂直于转轴的磁场分量激发的沿盘面的涡流会受平行于转轴(垂直于盘面)的磁场分量产生的安培阻力矩,即两方向磁场的减速效应不独立存在,故公式应包含sinαcosα交叉项[7,8].
基于上述考虑,磁场方向相对于陀螺仪转轴取向任意时减速系数k应满足如下关系
k=acosα+bsinα+ccos αsinα+d
(32)
式(32)中a、b、c、d为待定的角度无关参数.
2 实验验证
2.1 磁场方向与陀螺转轴方向垂直时的减速过程实验
在理论分析1.1中的式(9)表明陀螺仪的角速度随时间满足指数衰减关系,这种依赖关系可以在实验中进行实际检验.

图3 黄铜陀螺仪、亥姆霍兹线圈和高斯计

图4 陀螺仪角速度和时间关系曲线
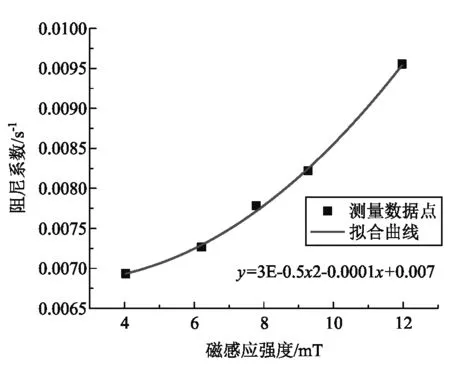
图5 阻尼系数k与磁感应强度关系曲线
实验中使用了如图3中所示黄铜制陀螺仪.先将陀螺仪加速到一定转速,之后迅速将其固定于亥姆霍兹线圈产生的匀强磁场之中,磁场方向垂直于陀螺仪转轴. 实验中使用光电门搭配挡光片测量计算旋转陀螺仪的速度,使用图3中的高斯计测量磁感应强度. 根据测量数据描绘磁场下的角速度(可转换为线速度)随时间依赖关系,并扣除无磁场时的影响.
实验中测量了多个磁感应强度下陀螺仪的减速过程,可将这些减速过程与式(9)进行比较分析. 图4是磁感应强度B=12 mT时的减速曲线,其中拟合曲线使用式(9)类型函数y=ae-bx+c进行拟合,可以看到拟合曲线和测量数据点匹配较好,陀螺仪在磁场中的减速过程可认为符合指数衰减规律. 也可将不同磁场下的减速过程数据(拟合曲线)对时间求导,研究减速过程的阻尼系数k与磁场应强度的依赖关系,从前面理论分析部分式(8)-(11)可以看出,阻尼系数与磁感应强度间应符合二次函数抛物线型依赖关系. 图5是由测量数据计算得到的阻尼系数与磁感应强度关系曲线,其变化趋势与式(14)相似的二次函数拟合曲线符合的较好.实验上佐证了前述理论部分的合理性.
2.2 直流电动机驱动实验

图6 匀强磁场中的直流电动机驱动实验仪器
通过引入直流电动机作为驱动,利用式(20)—(24)可以更直接地测量和分析特定角速度和磁感应强度下的电磁阻力矩. 实验中使用如图6中所示的130式永磁有刷直流电机,将其与陀螺仪链接后,放入匀强磁场中. 用“上行下行法”调节电流大小并记录与之对应的稳定角速度值.
固定磁场磁感应强度不变时,根据式(23),表征力矩大小的驱动电流应与陀螺仪稳定转动的角速度成线性关系,同时与外磁场磁感应强度成二次函数关系. 实验中改变磁场时难以保证陀螺仪转速稳定不变,因此只在固定外磁场条件下测量了转速稳定时陀螺仪旋转角速度和驱动电流的依赖关系. 实验中固定不同外磁场强度下进行了多组测量,驱动电流与陀螺仪稳定转动的角速度之间显示了很好的线性关系,图7中下图是磁感应强度为193.82 mT的测量数据,可以看到线性关系符合的较好.
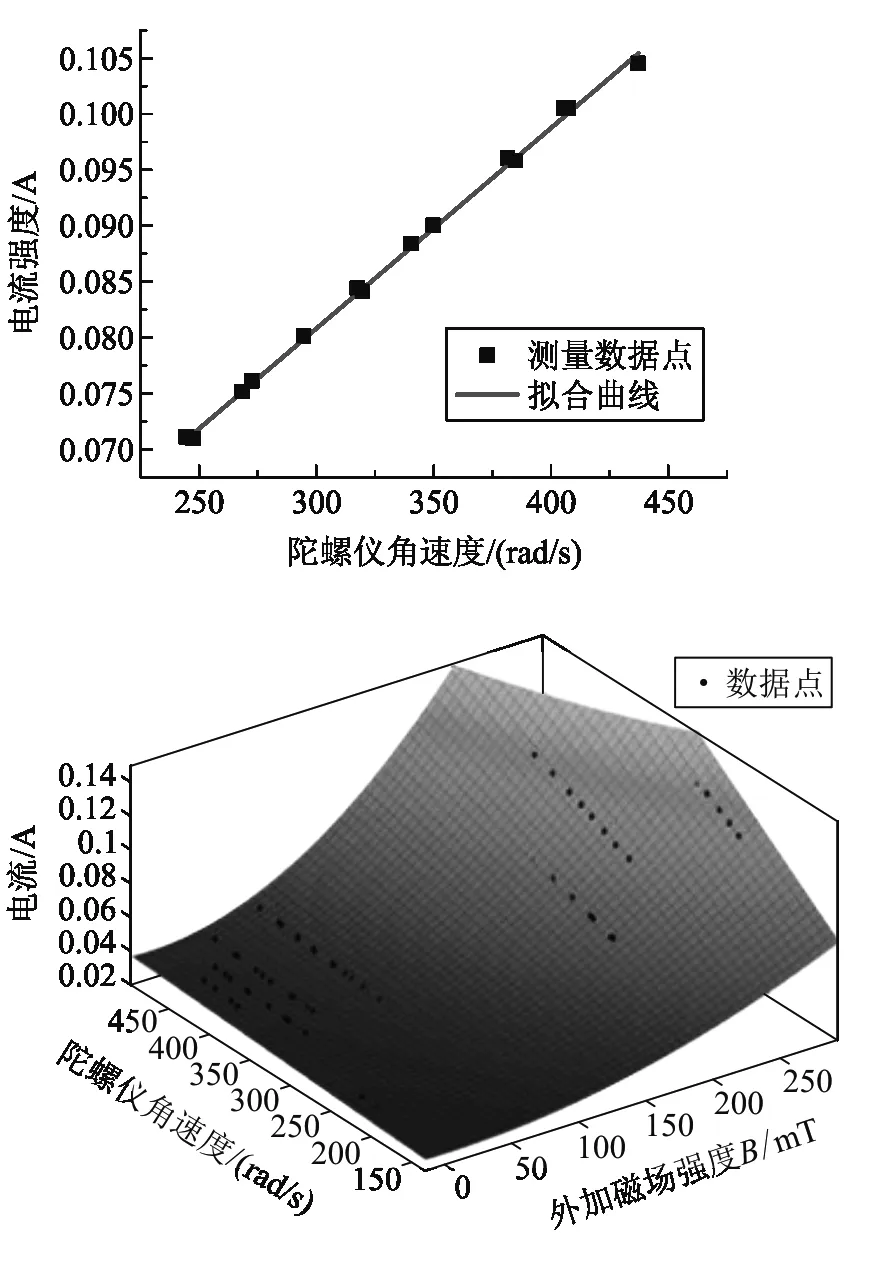
图7 直流电动机电枢电流与外加磁场和陀螺仪转速关系
将测得的电动机电枢电流、陀螺仪转速和磁感应强度在一个三维坐标中作图,数据关系用式(23)来进行拟合,从图7中右图来看,拟合曲线与实验数据点符合较好. 说明前述模型和假设条件基本合理,可用来解释陀螺仪在磁场中的减速过程.
2.3 磁场方向平行于陀螺仪转轴时的减速实验
当磁场方向与陀螺仪转轴平行时,根据前述理论分析,磁场范围限制在圆盘上的一个小区域中. 如图8所示,实验中将一个相对大且薄的铝盘作为陀螺仪圆盘,圆盘材质为6061铝,直径159.40 mm,厚度2.60 mm,直流电机提供驱动力,固定两块相同磁铁于圆盘上下两侧正对相吸,使磁感线垂直穿过圆盘上一个相对小的区域,磁铁尺寸为10 mm×10 mm×25 mm. 通过改变磁铁个数和间距以改变磁感应强度,通过改变磁场夹持装置位置以改变磁场到圆盘中心的位置. 使用光电门和挡光片测量不同磁感应强度下,圆盘稳定旋转时的角速度.

图8 磁场方向平行于陀螺仪转轴整体装置和光电门
实验中使用如图8中右图所示光电门测量稳态旋转状态的角速度平均值,利用稳定状态的电动机电枢电流和磁感应强度测量值可验证其相互依赖关系. 从测量数据可以看出,磁场大小和位置固定时陀螺仪圆盘稳态角速度和电动机电枢电流,即电磁阻力矩的依赖关系,和式(19)一致,符合线性关系,图9所示为磁感应强度B=100 mT时圆盘角速度和电动机电枢电流关系拟合结果,可认为符合线性关系.
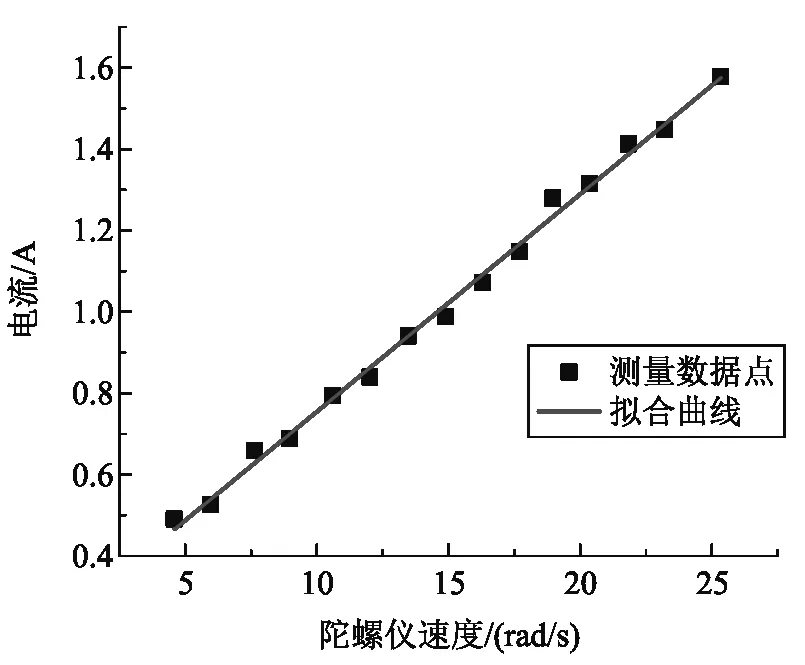
图9 磁场方向平行陀螺仪转轴且B=100 mT时角速度和电动机电流的关系
实验中通过改变盘片上下两侧永磁铁个数(保持最近两个永磁铁位置不变),改变圆盘上固定区域的磁感应强度,在不同磁感应强度下得到与图9类似的不同线性依赖关系的斜率. 图10是不同线性斜率与磁感应强度B的依赖关系,拟合曲线显示明显的二次函数特性,与式(23)和(24)的结果符合较好. 实验中高斯计存在零点漂移导致二次函数最低点有一定偏移.

图10 磁场方向平行于陀螺仪转轴时,阻尼系数与磁感应强度的依赖关系
1.2中的式(16)是以磁场区域相对陀螺圆盘无限小为基础的,根据式(19),若认为r的改变对系数α影响很小,使α几乎不变,那么有电磁阻力矩应与磁场区域距离圆盘中心距离r的二次方成正比的结论. 实验中通过改变磁场区域距离圆盘中心的距离r,得到了阻尼系数相对于r的关系,如图11所示,实验测量结果并不是明显的二次函数关系,在距离圆盘中心较近时近似线性关系,r>5 cm(圆盘半径大约7.5 cm)但仍在圆盘范围内时阻尼系数随r变化非常缓慢,趋近于饱和. 推测α应该依赖于r,在r较小时可以认为二者成反比关系,这一实验结果有待于严格的理论分析.

图11 电流和角速度的关系系数与磁场区域到圆盘中心距离r的关系
2.4 磁场方向相对陀螺仪转轴任意取向时的减速过程

图12 改变陀螺仪转轴与磁场方向夹角的减速实验装置
为了对1.5中得到的磁场方向相对于陀螺仪转轴任意取向时的减速过程满足的关系式(32)进行实验验证,实验中将陀螺仪加速后,以不同取向放入水平匀强磁场,使陀螺仪转轴与竖直方向夹角α. 如图12所示,通过自制的角度测量板可以近似测量夹角α,在不同角度下,通过光电门并配合挡光片测量陀螺仪的减速过程.
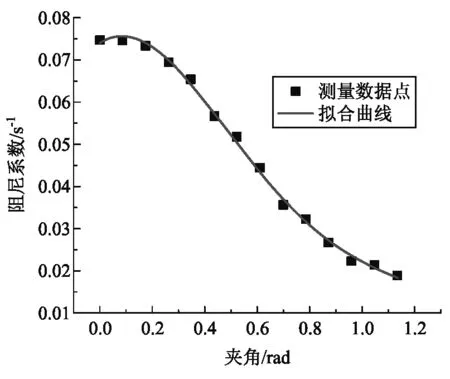
图13 陀螺仪转轴与竖直方向夹角α与阻尼系数关系
实验中保持磁感应强度在51.4 mT, 陀螺仪与竖直方向夹角α从0°到65°,每隔5°测量一次陀螺仪的减速过程,将测量计算得到的阻尼系数与陀螺仪转轴与竖直方向夹角α的关系用式(32)进行拟合,拟合结果如图13所示,可见阻尼系数与夹角α的依赖关系与式(32)符合的较好. 结合分析过程可以进一步推测若陀螺仪自身阻尼较小可忽略时,式(32)中的cosα项应可忽略[7,8].
2.5 陀螺仪减速过程与材料电阻率的关系
陀螺仪减速问题中,所用陀螺仪导体材料的电阻率涉及能量的耗散,电阻率变化时应会影响减速过程. 从前述理论分析式(23)和(24)可以看出,陀螺仪减速过程中的电磁阻力矩与电阻率成正比. 为验证这一推论,实验上需要保证在其他参数相同的状态下改变陀螺仪材料种类,这一实验还需要进一步的详细研究.
3 总结
IYPT题目普遍具有较强开放性和可研究性. 非铁磁性导体的陀螺仪在磁场中减速这个问题中,陀螺仪所用导体材料、陀螺仪尺寸、结构和磁场相关参数都是开放的,题中可变条件非常多,不易通过麦克斯韦方程组给出全面且统一的答案.
本文从无限长导体圆柱模型入手,通过合理的近似推导得到了陀螺仪转轴与磁场方向垂直和平行两种条件下电磁阻力矩与磁感应强度、角速度、电导率等参数的依赖关系的表达式,进一步分析得到了磁场方向相对陀螺仪转轴任意取向时陀螺仪减速阻尼系数的表达式. 为验证理论分析的合理性,首先使用量纲分析进行了初步验证,之后在实际实验中引入直流电动机提供驱动转矩,通过测量和数据分析比对,验证了基本模型推导得到的电磁阻力矩和减速过程的合理性. 通过理论和实验的分析可以得出,在陀螺仪转轴与磁场方向垂直和平行时,电磁阻力矩与磁感应强度的二次方和角速度的一次方成正比. 当磁场方向相对陀螺仪转轴任意取向时,阻尼系数满足式(32). 陀螺仪在磁场中受到的电磁阻力矩与陀螺仪电阻率成正比.

