基于磁梯度张量与Levenberg-Marquardt 优化的磁矩计算方法*
孙赫轩裴东兴*祗会强雒茁君
(1.中北大学仪器科学与动态测试教育部重点实验室,山西 太原030051;2.国网山西省电力公司电力科学研究院,山西 太原030051)
磁异常探测技术被广泛应用于地质勘测、变形监测、未爆炸物检测、近岸目标检测、医疗内镜定位、水下目标体定位等场景[1-5],具有极高的民用价值与军事意义。 磁性目标产生明显的磁场异常是磁异常探测的前提,而描述目标磁性特征最直观重要的物理量就是磁矩[6]。 在排雷或医疗等相关领域中应用磁异常探测技术时,磁矩计算误差引发的一系列偏差很可能会造成无法挽回的严重事故。 磁梯度张量相比于以往的磁场强度包含了更丰富的磁场信息,同时有效地克服了地磁场的影响,成为了国内外研究的热点[7-8]。
周建军[9]从磁性产生机理出发,推导了铁磁体磁矩计算公式,该方法使用起来较为繁琐,且仅适用于粗略估算。 Shutyǐ[10]对具有偶极磁矩的三球体和四球体系统进行了数值分析,研究了控制由交变磁场的幅值或频率变化引起的感应磁矩的可能性。Zhou[11]验证了感应磁矩与地磁场成正比,并设计了一种铁磁力矩的实时补偿方法,该方法可用于净化航磁测量中的磁环境。 Inamori T[12]使用地磁场信息计算磁矩,进而对卫星姿态进行磁补偿,使姿态稳定精度提高了5 倍。 Nara[13]研究了磁矩与位置矢量的夹角对磁矩的影响。 杨庆宇[6]、姜浩[14]等人优化了磁矩测量计算方法,原理上都基于磁场强度的测量,没有考虑到测量点处的磁场强度中叠加了地磁场值,这给磁矩计算带来很大误差。 周[15]提出了磁场积分法和最小二乘正则化方法反演铁磁物体的固有磁矩,初步解决了固有磁矩引起的感应磁矩问题。 Chadebec O[16]将磁矩量法与有限元法相比,认为该方法具有较高的分辨率和高精度的复杂场计算。 但使用这种方法要对物理现象和数值方法本身有良好的了解,需要较高的操作技巧。
本文提出了一种基于磁梯度张量与Levenberg-Marquardt 优化的磁矩计算方法。 该方法利用磁偶极子模型,采用磁梯度张量概念与Levenberg-Marquardt 优化算法(下文简称L-M 算法)结合的方式,有效消除地磁场的干扰与测量计算奇异点,提高磁矩计算精度与抗噪声能力,具有更高的鲁棒性。 为后期针对磁性目标的反演识别、三维重建等更深层次磁异常数据的应用提供了理论基础与经验参考。
1 磁偶极子模型与磁梯度张量理论
为简化磁场问题,可以将磁场目标抽象为一个仅具有磁性特性相关的理想化模型——磁偶极子。理论上讲,任意复杂源都可视为由一定数量偶极子组成,这为复杂源的加入及复杂环境下的瞬态场计算提供条件[17]。 测量距离约为被测物尺寸2.5 倍以上时,磁偶极子模型可用于替代形状较为规则的磁性物体[18]。 假设磁偶极子磁矩为m,则在距离偶极子r处的磁感应强度可以表示为:

式中:μ0为真空磁导率,ro为位移r的方向向量,r=|r|,mo为磁矩m的方向向量,m=|m|。
磁梯度张量是磁场矢量正交三分量在空间各个方向上的变化率构成的二阶张量[19],共九个分量,可表示如下:

地磁场强度约为50 000 nT,且会随空间时间发生变化,但短时间小区域内可认为是一个恒定磁场,其梯度值很小[20-21],约小于0.02 nT/m。 在无源静磁场下,静磁场磁感应强度的散度和旋度都等于零[22],故磁梯度张量G可视为仅含有Bxx、Bxy、Byy、Bzx、Bzy5 个独立分量。 即:
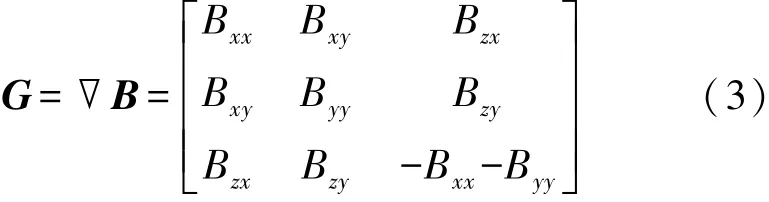
2 磁矩测量模型与优化算法
2.1 基于十字形磁传感器阵列的磁矩测量模型
磁性目标的磁矩是一个既有大小又有方向的矢量,是描述物体磁性特征最直观的物理量。 磁矩矢量可以写做磁矩模值m与磁矩方向向量mo的乘积,也可依照坐标系方向分解为正交三分量mx、my、mz。
磁偶极子磁矩测量模型示意图见图1,设磁矩为m=(mx,my,mz)的磁偶极子位于坐标系原点,则根据式(1)和式(2)可得在距离磁偶极子r=(x,y,z)处的测量点P的磁梯度张量5 个独立元素可表示为:

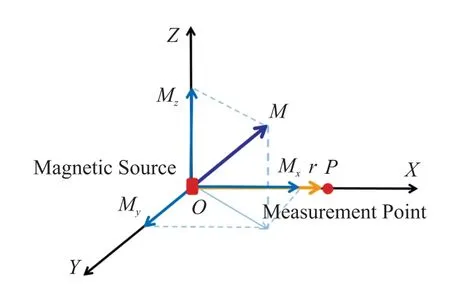
图1 磁偶极子磁矩测量模型
磁梯度张量测量系统采用十字架结构,如图2所示,测量中心位于十字架中心,XY轴分别与十字架两个轴平行,Z轴向上垂直于十字架所在平面,四个磁传感器分别位于十字架四个顶点,传感器的坐标轴与测量系统坐标轴保持一致。
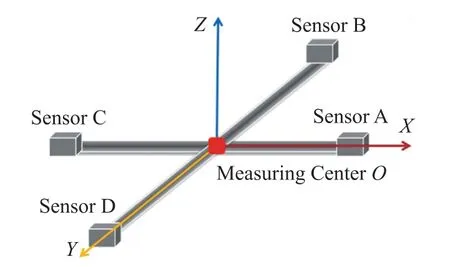
图2 十字形磁传感器阵列
利用差分代替微分的思想,可得磁场中测量中心处的磁梯度张量独立分量值为:

式中:Sij代表传感器i在j轴方向上的磁场分量,d为十字架基线长度。 将以上独立分量代入式(3)可得测量中心点处的磁梯度张量。
在同一磁场环境下联立式(4)和式(5)中任意三个分量,可以使用解析方法计算出磁矩矢量m=(mx,my,mz)的值。 之后可以解出磁矩模值m和方向矢量mo:
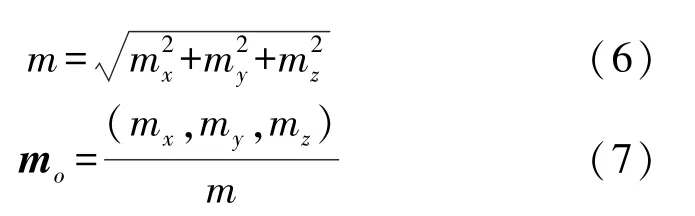
然而求解过程中发现,不管如何选取组合其中的三个分量,在某些位置都会出现方程组自由度不足的现象,导致出现奇异点。
2.2 基于Levenberg-Marquardt 算法的磁矩解算优化
针对解析方法求解会出现奇异点的问题,考虑使用L-M 优化算法对磁矩相关数据进行求解。 LM 算法是一种迭代优化算法,综合了高斯牛顿法局部收敛和梯度法全局收敛的特点,解决了梯度法收敛速度慢的问题,也优化了高斯牛顿法的Hessian矩阵不正定的问题[23-24]。
以磁梯度张量测试系统测的测量点张量数据作为范例,磁偶极子模型计算的包含磁源磁矩信息的磁梯度张量数据作为目标数据,运用L-M 优化算法进行优化处理。
令F(mx,my,mz)为目标函数,形式见下式:

利用L-M 算法对该非线性目标函数进行参数优化,求(mx,my,mz)使得输出的如下最小二乘表达式成立:

设定初值对目标函数做非线性最小乘二拟合,所得(mx,my,mz)即为磁性目标的磁矩优化计算结果。
3 仿真分析与实验验证
为验证所提方法的反演性能,本文使用MATLAB软件进行多组仿真实验,仿真对象针对可能影响反演结果的地磁背景场、测量系统所在位置、环境噪声等因素。 仿真中预设磁性目标磁矩模值为1 000 Am2,磁倾角为π/4,磁偏角为π/6。 地磁场取经验模值50 000 nT,地磁倾取-0.925,地磁偏角-0.30进行模拟。 十字架磁梯度张量测量系统基线为0.4 m,传感器精度为10 nT。 为避免偶然性,测量系统中心在Z=3 m 的平面内半径为5 m 的圆形轨迹上等间隔取64个测量点,对位于坐标系原点处的磁源点磁场信息进行测量,测量系统位置示意图见图3。
图3 测量系统位置示意图
利用测量点的磁场信息,分别使用姜浩等人提出的基于磁场强度B 的磁矩计算方法(简称MOB)、基于磁梯度张量的磁矩计算解析方法(简称MOG)、和本文所提优化方法对磁矩进行计算,比较分析其磁矩反演效果。 仿真实验中,采用计算方向向量与理论方向向量之间的夹角度数来作为衡量磁矩方向反演效果的评价指标,采用计算模值与理论模值之间的相对误差作为衡量磁矩大小反演效果的评价指标。
3.1 地磁背景场影响分析
在地球磁场背景下,磁传感器测得的磁场强度为磁异常信息与地球磁场的混叠。 由于地磁场强度的数量级远大于磁异常强度,如果不能很好的分离地磁场与目标信号,将会对磁矩反演造成困难与误差。 本组仿真对同一组传感器在同一时间测量到的磁场数据分别采用方法B 与本文所提方法进行磁矩求解。 仿真结果见图4 与图5。

图4 测量点的磁矩方向向量角度误差
由图4 和图5 可知,基于磁感应强度的磁矩求解结果与地磁场方向有明显的相关关系,地磁场方向上误差值最大,说明此方法受地磁场影响极大,无法将磁源信息从背景场中提取出来。 而利用磁梯度张量方法的结果与地磁场无明显相关关系且角度误差与相对误差都较小,有效解决了磁测环境背景地磁场干扰较大且难以分离的问题。
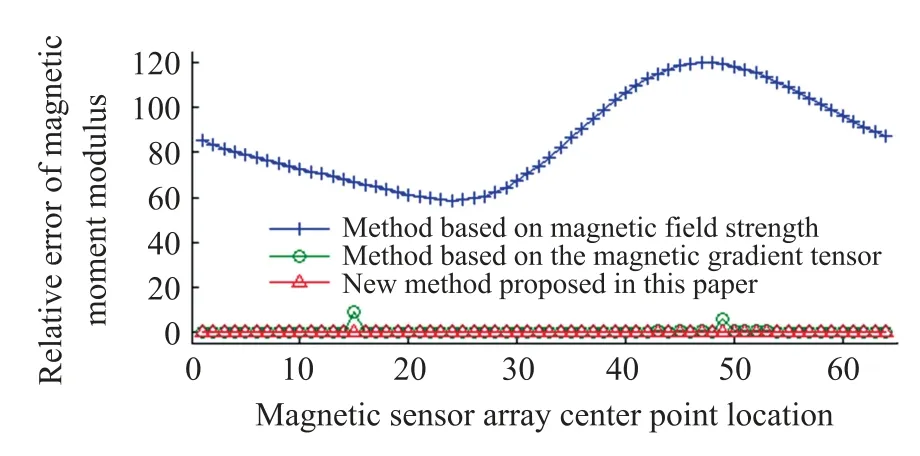
图5 测量点的磁矩模值相对误差
3.2 测量系统位置影响分析
方法应用中发现,测量系统与磁源点相对位置不同,磁矩反演效果也可能不同。 由于上一节证实方法B 存在明显缺陷,故在下文主要对基于磁梯度张量的磁矩计算方法进行探究。 本组仿真针对不同的测量系统位置,分别采用解析方法与L-M 优化算法对磁梯度张量测量系统的数据进行后续处理,分析两种方法受测量系统位置的影响情况,仿真结果见图6 与图7。
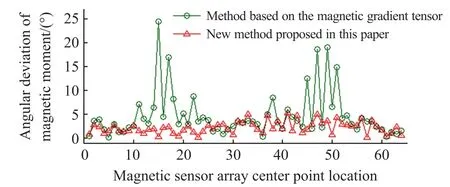
图6 测量点的磁矩方向向量角度误差

图7 测量点的磁矩模值相对误差
由图6 和图7 可知,使用解析方法处理梯度张量数据时,在特定坐标轴附近存在误差明显异于常值的现象,而采用了L-M 优化算法的方法则很好的解决了这一问题,数据波动平稳,误差分布均匀,处理结果非常理想,使磁矩在磁源点附近有效距离内全方位精准可测。
3.3 环境噪声影响分析
实际测量中存在的环境噪声会导致磁矩反演困难,因此抗噪声能力是衡量一个方法实用性的重要指标。 在传感器测量值中加入不同信噪比的高斯白噪声。 高斯白噪声存在随机性,为观测普遍规律,保持其他条件不变,每种信噪比情况下选取64 个测量点的数据,并对64 组数据求取均值以代表此信噪比下解析方法与L-M 优化方法的反演效果。 仿真结果见图8 和图9。
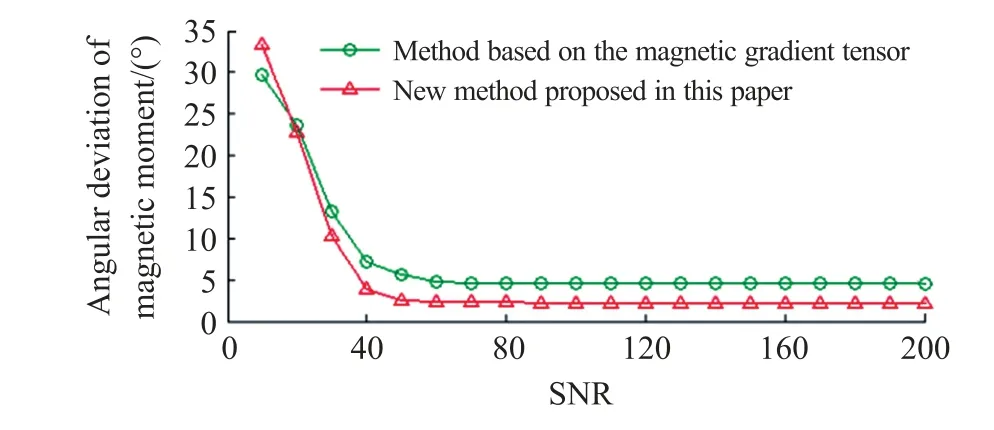
图8 不同信噪比下的磁矩方向角度误差

图9 不同信噪比下的磁矩模值相对误差
由图8 和图9 可知,随着高斯噪声信噪比的增大,磁矩计算的误差迅速减小。 综合来看,当信噪比大于等于60 dB 时,反演误差达到最小并趋于平稳。对比两种方法,所提方法的数据总是先于解析方法平稳,且总体误差更小,抗干扰能力更强。 这是由于所提方法在解算过程中使用数值法计算完成,对噪声有更强的鲁棒性。
3.4 实验验证分析
选择开阔无扰动、地磁场稳定的室外环境,划定空间坐标系,X轴方向为地理东向,Y轴方向为地理南向,Z轴垂直向下。 已知尺寸为100 mm×100 m×50 mm,出厂磁矩参数范围为510 ~525Am2,方向沿A 面垂直向上的铁磁体安装在原点处,由于本文算法基于磁偶极子模型,校准后的磁梯度张量测量系统需位于磁体0.25 m 之外的位置。 磁性目标姿态变换三次,本次实验测量系统的位置在距磁铁直线距离为1.5 m~3.4 m 的范围内,每个磁铁姿态下随机放置40 个测试系统位置,采用上位机系统实时采集测量点处的多组磁场数据。 分别使用MOB、MOG和本文所提方法计算磁矩,并与出厂磁矩参数进行对比,验证本文方法的可行性;在每一种磁性目标姿态下多次变换测量系统位置,查看磁矩计算结果的变化情况,验证所提方法的可重复性。
由表1 可知,实验结果基本与仿真情况相符。MOB 方法混叠了地磁场,误差极大。 MOG 方法测量结果处于可接受范围内,但稳定性较差,个别位置偏差较大,在少量样本情况下需慎重使用。 使用本文方法对三组姿态磁体反演得到的磁矩幅值数据稳定,且处于厂家给出的磁矩范围内,认为实测结果有效,且数据波动范围可接受,能够满足工程需要。 偏角误差的实测值比仿真值要大一些,下一步实验拟使用精度更高的磁传感器,设计更优良的测量系统,选择更理想的测试环境,预计可进一步提高所提方法的应用精度。

图10 基于磁梯度张量测量系统的磁矩反演实验
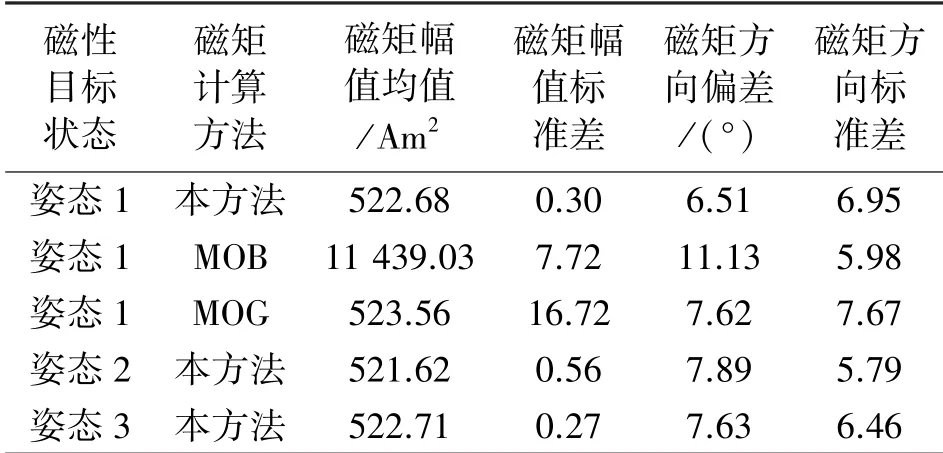
表1 磁矩计算平均相对误差与平均标准差表
4 结论
本文提出了一种基于磁梯度张量与Levenberg-Marquardt 优化的磁矩计算方法,优化了现有的磁矩计算方法使用不灵活、精度较低、受地球背景磁场影响大的问题。 该方法采用磁梯度张量概念消除了地磁背景场的干扰,采用L-M 优化算法解决了解析方法求解存在奇异点,误差相对较大的弊端。 仿真实验与现场实验的结果表明,本文所提磁矩计算方法相比于传统方法消除了地磁背景场干扰,解决了奇异点问题,可以实现地磁环境和一定信噪比的高斯环境噪声情况下的磁矩快速反演。 整体测量方案方便简单,精准易用,具有较强的可行性与可靠性。 所提方法同样适用于其他结构类型的磁梯度张量测量系统。 高精度抗噪声的磁矩计算技术为后期针对磁性目标的反演识别、三维重建等更深层次磁异常数据的应用提供了理论基础与经验参考。

