电容式力感知牙周探针设计建模与实验研究*
唐忠林杨建华雷宏伟
(1.陕西工业职业技术学院航空工程学院,陕西 咸阳712000;2.西北工业大学自动化学院,陕西 西安710072;3.西安苏茂医疗科技有限公司,陕西 西安710077)
牙周病是最普遍的口腔健康问题之一[1],牙周探诊是临床公认的牙周病检测手段,其核心工具就是牙周探针[2-3]。 牙周探针的基本结构如图1(a)所示,由工作尖和手柄组成,其工作尖形如一把以毫米为单位的勾形尺,可以用来检查牙周袋深度等牙周健康状况,如图1(b)所示。
通常把图1(a)所示的牙周探针称为第一代探针[4],其操作全凭医生的经验和手感,轻则探不到底,重则伤害牙龈,准确性和体验性都有所欠缺[5-6]。 在第一代牙周探针的基础上增加恒力装置,发展出了第二代牙周探针[4,7];进而与计算机技术相结合,诞生了第三代牙周探针,实现了牙周探诊结果的自动化读取、保存和呈现,典型产品为美国的佛罗里达探针[4,8]。

图1 牙周探针的基本应用
第二代和第三代牙周探针都采用了探诊力恒定控制技术[9-10],一般把探诊力限制在0.25 N 左右[11],减小了医生操作的主观性对探诊结果的影响,患者体验也更加友好。 但是恒定探诊力也存在缺陷,比如有的患者龈下结石多,探诊阻力大,有的患者牙龈炎症重,探诊阻力小,在施加探诊力时并不能一概而论,否则会破坏探诊准确性和结果一致性[2-3,11-13]。
在临床上,探诊力被公认为是影响牙周探诊质量的最重要因素[3,11,13]。 鉴于探诊力恒定控制存在的不足,能够实时检测探诊力的牙周探针开始受到研究人员的青睐,见诸报导的方法包括薄膜式压力传感器[14]、弹簧杠杆式探诊力传感器[15]、摩擦式探诊力传感器和气压式探诊力传感器[10]等。 这些方法的缺点在于一是结构比较复杂,二是消毒灭菌不便,到目前为止并没有转化为可用的产品。 本文研究开发电容式力感知牙周探针,利用探诊力作用下牙周探针的挠曲效应,设计差动电容式探诊力传感器,实时检测施加在探针工作尖上的探诊力,有利于医生根据患者的实际情况把探诊力控制在适当的范围内,提高牙周探诊的准确性,改善患者体验,并且结构简单,消毒灭菌方便。
1 设计建模
1.1 结构设计
虽然公认0.25 N 是合适的探诊力度,但也有研究认为,针对患者不同的龈下阻力情况,0.15 N~0.5 N 范围内的探诊力都是可以接受的[2,7,11]。 要实现探诊力的连续监测,必须采用传感器技术。 根据牙周探针的使用情况和医疗器械的消毒要求,差动式平板电容传感器是一个理想的选择。 根据我国医药行业标准YY/T 1622.1—2018 对牙周探针的通用要求,结合口腔门诊常用的第一代牙周探针的工作尖尺寸规格,设计电容式力感知牙周探针的验证结构如图2(a)所示,包括:①上下平板电极,②浮动平板电极,③探针工作尖,④上下壳体盖板,⑤上下电容隔板等,各部件按图2 所示的相对位置进行粘接固定。 其中,浮动平板电极的右端与探针工作尖刚性连接;浮动平板电极和上下平板电极之间用厚度相同的隔板隔开,构成具有对称结构的差动式电容传感器;三个平板电极的左端均设计有电气引脚。 平板电极和探针工作尖的材料均采用奥氏体不锈钢,其他零部件的材料均采用符合医用标准的ABS 工程塑料。 所设计探针各零部件的关键结构尺寸和装配尺寸如图2(b)所示。 工作时,医生握持探针尾部,将探针工作尖垂直插入牙周袋进行牙周探诊,探诊力F沿轴线施加于探针工作尖端面,引起浮动平板电极的挠曲变形,导致浮动平板电极和上下平板电极之间的极间距沿反向改变,形成上下电容的差动变化,可以据此实现探诊力的实时检测。 在此应变系统中,浮动平板电极的挠变原点位于上下隔板的夹持前端面,如图2(b)中(x,y)坐标系的零点位置处。
1.2 建模与仿真
如图2 所示,探针工作尖和浮动平板电极构成异形的单端悬臂梁结构。 根据梁的变形理论,可以得到在探诊力F作用下,浮动电极的挠曲线表达式:

式中:(x,y)坐标系如图2(b)所示,EI为浮动电极的抗弯刚度,其中E为电极材料的弹性模量,I为电极的截面惯性矩,对于浮动电极的矩形截面,有:

F′为将探诊力F折算到浮动平板电极右端面的挠曲力,方向垂直于电极平面。 根据力矩平衡公式,可得F′的计算公式为:

以上公式中,W、T、L、H、B、θ的尺寸关系如图2(b)所示;G为浮动电极和探针工作尖的重量;K1、K2、K3为修正系数,分别用于修正探针工作尖的有限刚度、探针工作尖的不规则形状、浮动电极和探针工作尖重力分布的不均匀对计算结果的影响。

图2 电容式力感知牙周探针的结构设计

表1 SolidWorks 静应力仿真参数
由于探针工作尖的不规则形状和非均匀尺寸,要精确求解K1、K2、K3的值比较困难,本文采用SolidWorks 静应力仿真的方式对以上三个参数进行估计。 对图2(b)的结构,仿真模型的参数如表1 所示。 具体方法为:在0.1 N~0.5 N 范围内,以0.05 N为步长,总共产生9 个实验探诊力,记为F0.1,F0.15,…,F0.5;将某一实验探诊力Fx作用于探针工作尖端面,记录浮动平板电极右端面挠度,再在浮动平板电极右端面施加一个使其右端面挠度与之相等的挠曲力F′x,这样可以找出与9 个实验探诊力对应的折算力F′0.1,F′0.15,…,F′0.5。 在以上9 对力中任取三对组成方程组,可得到K1、K2、K3的一组解,如式(4)所示:
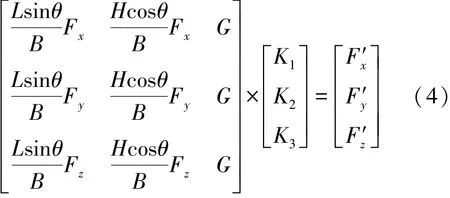
式中:(Fx,F′x),(Fy,F′y),(Fz,F′z)为从以上9 对力中任意抽取的三对,一共可求得84 组K1、K2、K3的解。 本文求取了11 组解,然后求平均,得到K1、K2、K3的的估计值为0.98,1.75 和0.95。 图3 给出了根据式(1)得到的计算挠曲线和仿真挠曲线在探诊力为0.1 N,0.3 N 和0.5 N 时的对比图。

图3 挠曲线计算值和仿真值的对比
从图3 可以看出,根据式(1)~式(4)计算得到的挠曲线和仿真结果具有较高的一致性,在浮动平板电极的整个悬臂段,最大相对误差不超过±4.5%,且误差曲线在平板电极的长度方向有正有负,在以积分方式计算差动电容时可以相互抵消。 其中,主要误差来自于计算模型并没有考虑上下电容垫板在有限刚度情况下的挤压变形。 此时,浮动平板电极和上下平板电极之间的电容C1和C2可分别由以下公式计算:

式中:D为浮动平板电极和上下平板电极之间的距离,ε为空气的介电常数。 浮动平板电极和上下平板电极之间的电容均由两部分组成:一部分来自于浮动平板电极悬臂梁的活动部分,其电容值取决于在探诊力作用下浮动电极的挠曲线,用积分式计算;另一部分来自于浮动平板电极的固定部分和电容电极引线,为探针初始固定电容,上下电容值分别用C10和C20表示。 对于上下对称的探针电极和引线结构,C10=C20,得到在探诊力F作用下牙周探针的差分电容如式(7)所示,其中挠度y与活动电极沿长度方向的x坐标的关系见式(1)。

2 实验分析
2.1 实验设置
用ABS 板材和不锈钢板材根据图2 制作了电容式力感知牙周探针的验证结构,如图4 中的嵌入式小图所示。 各平板电极和盖板、隔板之间用ergo1309 结构胶粘接,粘接后在室温下用5 kgf 力静压4 h 后使用;探针工作尖为从上海伟荣医疗器械购买的牙周探针上切割而来,针头刻度为3-6-9-12 mm,使用不锈钢焊锡焊接到浮动平板电极右端的卡槽,形成刚性连接;各电极尾部的电气引脚上分别焊接20 cm 长的导线,导线芯径1.12 mm;把开尔文夹夹在电极导线的尾部,用精密LCR 数字电桥(同惠,TH2827C)在20 kHz 频率下分别进行六次校准和测量,测得自由状态下探针的浮动平板电极和上下平板电极之间的初始电容平均值分别为C10=9.184 pF 和C20=9.307 pF,两者并不相等,制造误差主要来源于上下隔板的厚度误差和结构胶涂抹厚度误差。

图4 牙周探针的电容式力感知实验
牙周探针的电容式力感知实验设置如图4 所示。 牙周探针1 夹持到虎台钳2 上,探针工作尖垂直向下,作用在克力计3(伊莱科,ATG-50-1)的力臂测力点上。 克力计水平固定于精密三轴移动平台4(润佳气动,LD90-LM)的工作面。 调整精密三轴移动平台工作面的高度,在探针工作尖产生模拟探诊力。 在每一个测力点,用精密LCR 数字电桥5(同惠,TH2827C)先测量浮动平板电极和上平板电极之间的电容C1,再测量浮动平板电极和下平板电极之间的电容C2。
2.2 实验结果
一次实验过程包括三个实验周期,每个实验周期包括探诊力的升程和回程两个阶段。 在每个实验周期的升程阶段,探诊力从0 N 上升到0.5 N,每隔0.05 N 进行一次测量,每两个相邻测力点的时间间隔为2 min,两点之间的测试力平稳过渡;回程阶段探诊力从0.5 N 下降到0 N,测力点和测试方法与升程阶段相同。
图5(a)给出了三个实验周期中每个测力点对应的浮动平板电极和上下平板电极之间的电容C1和C2的测量值。 在三个实验周期,C1和C2的变化表现出较好的重复性和一致性,在十一个测量点,C1的最大标准差为0.007 8,C2的最大标准差为0.005 9,均不到均值的0.1%;在升程阶段,随着探诊力增加,浮动电极平板向上挠曲,与上平板电极之间的有效距离减小,与下平板电极之间的有效距离增大,表现为电容C1单调增加,电容C2单调减小;在回程阶段,随着探诊力减小,浮动电极平板向初始位置回归,C1好C2的变化方向与升程阶段相反。
图5(b)给出了电容式力感知牙周探针的理论模型计算值和验证结构测量值的对比情况。 图中不带标记点的直线为根据式(7)计算得到的探针差分电容随探诊力的变化情况;带标记点的实线分别是牙周探针的验证结构在三个升程阶段测量得到的差分电容随探诊力的变化情况,同色且带同样标记点的虚线为对应的三个回程阶段测量得到的差分电容随探诊力的变化情况,在计算时对上下平板电容的初始误差进行了修正,修正方法为:
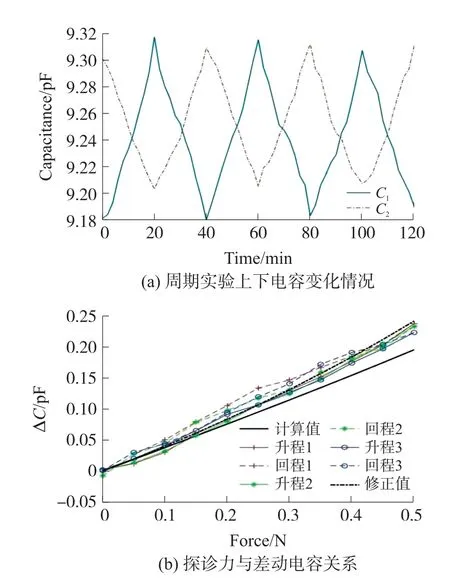
图5 探针电容与探诊力的对应关系

式中:C1和C2分别为上平板电容和下平板电容的实测值。
从图5(b)中的理论模型计算值可以看出,采用差动式平板电容传感器检测探诊力,在理想情况下差分电容和探诊力之间呈线性关系,设备结构简单,信号处理方便;实际测量值和模型计算值之间存在偏差,探诊力在0.2 N 以下时,计算值和测量值吻合较好,随着探诊力增加,测量值和计算值之间的偏差增大,全量程平均偏差为12.31%。 这是由于在建立式(1)~式(7)的理论模型时,并没有考虑探头塑料附件的有限刚度。 探针验证结构的浮动平板电极和上下平板电极之间用1 mm 厚度的ABS 塑料板和一层ergo1309 结构胶隔开,在探诊力作用下,浮动电极对隔离层产生挤压变形,浮动电极的实际挠度大于理论挠度,表现为差分电容的测量值总体上正偏离于计算值,并且随着探诊力加大偏离程度也加大,但是计算值和测量值总体上趋向一致。 不失一般性,对所设计的牙周探针验证结构,以探诊力大小为拟合权重对计算曲线进行修正,通过最小二乘法拟合,可以得到更精确的差分电容计算模型,如式(9)所示:

式中:F为探诊力,ΔC为根据式(7)得到的计算值。修正值曲线如图5(b)中不带标记点的虚线所示,与实测值吻合良好,全量程平均偏差降为2.49%,可以满足实际应用要求。
3 结束语
针对当前牙周探针在探诊力控制方面的不足,鉴于探诊力被公认为是影响牙周探诊质量的最重要因素,本文提出一种电容式力感知牙周探针的解决方案,利用探诊力作用下探针工作尖的挠曲效应引起的差动电容变化来实现探诊力感知。 设计了电容式力感知牙周探针的验证结构,建立了探诊力作用下具有不规则形状的探针工作尖的挠曲模型,导出了探诊力和差动电容之间的求解方程,并通过仿真和实验对模型和方程进行了验证。 仿真表明,所建立的探针工作尖挠曲模型与SolidWork 静应力仿真结果具有较高的一致性,在浮动平板电极的整个悬臂段,最大相对误差不超过±4.5%;实验表明,导出的探诊力和差动电容之间的求解方程的计算结果与实际实验数据之间趋向一致但存在偏差,全量程平均偏差为12.31%,以探诊力大小为拟合权重并通过最小二乘法对计算曲线进行修正后,全量程平均偏差降为2.49%,可以满足实际应用要求;多次重复实验的结果一致性较好,上平板电容C1的最大标准差为0.007 8,下平板电容C2的最大标准差为0.005 9,均不到均值的0.1%。
当前的研究工作只是电容式力感知牙周探针研发的理论和基础部分。 研究结果表明,所提出的针对牙周探诊的探诊力检测的技术方案具备可行性。 下一步还需要继续完成电容式力感知牙周探针的产品性开发,包括利用CAD 技术和3D 打印技术设计加工探针产品壳体,利用嵌入式技术开发包括无线通信和电容检测等功能在内的探针处理电路,开发与牙周探针配套的桌面或移动平台的病历管理软件等。 通过产品开发,有利于为医生提供更先进的牙周探诊工具,提高牙周探诊的准确性,改善患者体验。

