基于信道状态特征的手势动作识别技术研究*
吴哲夫邵承贤龚树凤*毛科技吕跃华
(1.浙江工业大学信息学院,浙江 杭州310023;2.浙江工业大学计算机科学与技术学院,浙江 杭州310023;3.浙江省科技信息研究院,浙江 杭州310006)
近年来,随着物联网的不断发展,以人为中心的人机交互模式成为人们生活中不可或缺的一部分。人机交互模式中,手势识别作为人与机器重要的交互手段,吸引了许多研究者的注意。 根据采集数据的方式,当前手势识别的方式可以分为三种:基于图像分类处理的手势识别、基于传感器的手势识别以及基于无线信号的手势识别。
基于图像分类处理的手势识别主要利用摄像机对人体手势进行拍摄,并通过计算机图像处理的方法将手势和背景进行分割,从而识别手势。 如Guillaume 等人[1]用Kinect 摄像机拍摄人体手势,并利用k-曲率算法以及动态时间归整对手势进行分类,准确率达到了92.4%;宋一凡[2]等人利用姿态估计和神经网络结合的方式对拍摄手势图像进行分类,识别准确率达到了98%。 基于图像分类处理的手势识别虽然能够无接触的对人体手势进行识别,但在光照不充足的室内准确率会有所下降。
基于传感器的手势识别主要是通过人手持传感器(例如加速度仪)或者将传感器安装在手上来获取相关动作信息。 如吴常铖等人[3]利用装有弯曲电阻片的数据手套获取手部动作信息并利用神经网络进行分类,识别准确率能够达到99.2%;鲍磊等人[4]提出一种融合四路表面肌电和三轴加速度传感信息的识别方法,对4 名受试者的6 种手语手势最高识别率可以达到91.2%。 谢仁强等人[5]将复杂手势看成简单手势的组合,利用加速度传感器实现了99.75%的识别准确率。 传感器能够获取到人体手部细微的动作变化,具有很高的灵敏度,然而其需要专用的传感器设备并且接触人体手部才能获得精确的动作信息,这限制了基于传感器手势识别在日常生活中的应用。
基于无线信号的手势识别主要利用手部动作引起的信号变化来识别手势[6-7]。 由于室内WiFi 信号的普及,利用WiFi 信号进行手势识别不受光照影响,能够无接触、配置简单和成本低,在日常生活中与其他方式相比具有很大的优势,已成为基于无线信号进行手势识别的一个热门方向。 如Heba Abdelnasser 等人[8]提出的WiGest 通过识别信号强度RSSI 上升沿和下降沿来判断动作,并结合多AP 提高手势识别的准确率,在三个AP 情况下提高到96%。 随着CSI-Tool 工具的开源[9],研究人员可以利用商用笔记本获取到更细粒度的WiFi 信号-信道状态信息CSI,因此越来越多的研究人员利用CSI来进行手势识别。 潘旭[10]利用一维卷积神经网络从获取到的CSI 数据中获取手势特征,准确率达到了93.03%;刘佳慧等人[11]利用LSTM 算法对采集到的CSI 数据进行分类,准确率达到了82.75%;Sheng Tan 等人[12]设计了环境噪声消除机制来减弱室内环境噪声对CSI 的影响,实现了93%的识别准确率。
上述基于WiFi 的手势识别方式,仅仅只是利用了CSI 信号中的幅度信息,没有使用其中的相位信息。 由于相位信息对周围环境的感知比幅度信息更敏感,因此引入相位信息应该能够有效提高手势识别的准确率。
为了充分利用CSI 信号特征,本文设计了一种基于CSI 幅值和相位结合的手势识别系统。 首先采集了包含30 个子载波的CSI 数据,并采用主成分分析法PCA 进行降维。 由于人体手势在一个时间段从动作起始时间到结束时间的信号曲线是需要进行分析的数据部分,为了提取这段时间的动作曲线,系统利用设计滑动窗口计算曲线的方差,根据滑动窗口内方差的峰谷值确定动作的起始时间和结束时间,从而获取动作曲线。 最后将CSI 幅值和相位结合作为动作特征进行了多种机器学习算法的训练,实现了六种手势动作的识别,并在不同距离下验证了所提算法的有效性。
1 系统原理及实现方法
人体的不同手势动作会对CSI 信号产生不同的影响,图1(a)和图1(b)分别表示人体做两次相同手势动作和不同手势动作时对CSI 信号波形产生的影响。
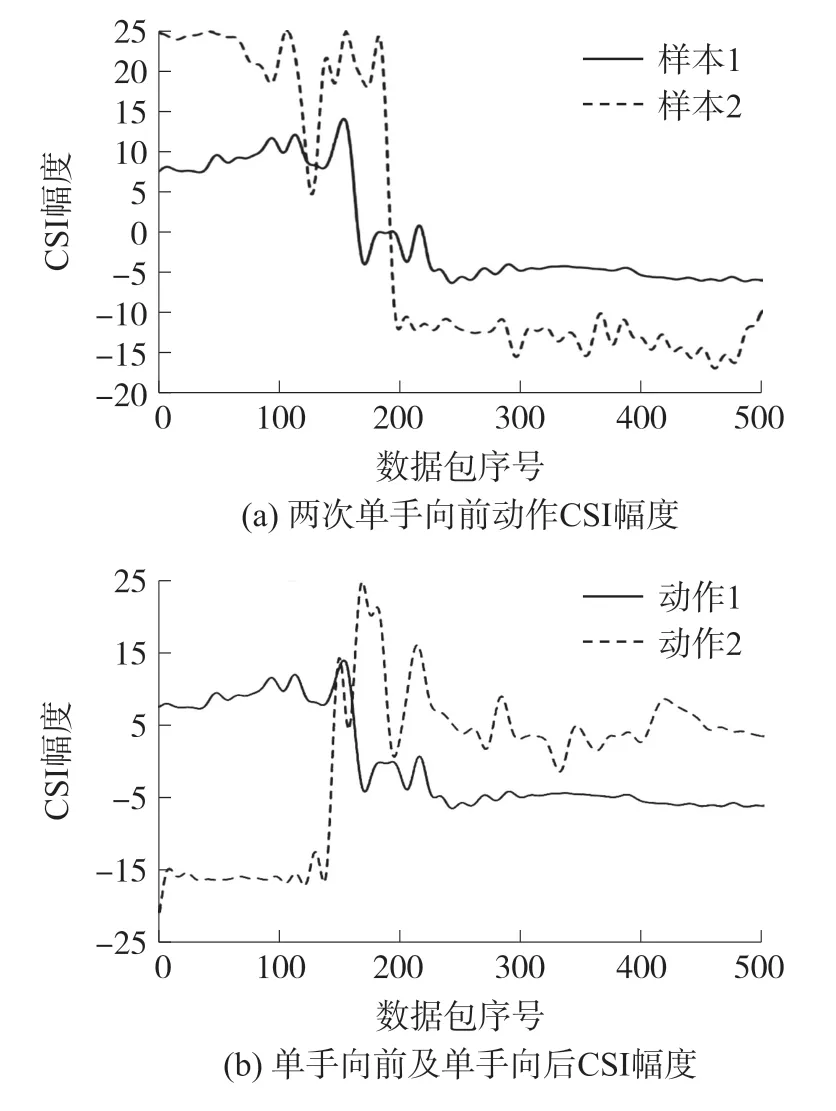
图1 手势动作对CSI 影响
从图1 中可以看到两次相同手势动作呈现的曲线具有明显的相关性,而单手向前和单手向后两个不同动作呈现的曲线具有明显差异。 因此可以根据信号曲线的波形来判断不同的手势动作。
图中还可以看出,在人体动作开始前和结束后信号会保持平稳,而这种平稳的信号无法为识别手势提供有用的信息,因此如何从一段信号中确定动作的起始点和结束点成为本文要解决的难点之一。另一个重要的问题在于CSI 包含了30 个子载波,每个子载波都有各自的幅值和相位信息。 如果对所有的子载波进行处理会导致数据的繁琐和冗余,因此本文还需要对获取的CSI 数据进行降维处理,从而简化处理数据。
为了解决上述提到的问题,并结合CSI 幅值和相位进行手势识别,本文设计了一种基于CSI 的人体手势识别系统,系统框图如图2 所示。 系统分为数据预处理阶段、离线阶段和在线阶段。 数据预处理阶段系统首先利用CSI 数据采集平台提取CSI 信号的幅值和相位,并对幅值和相位进行去噪和异常值处理。 并且,对处理后的CSI 数据进行子载波降维,从降维后的CSI 数据中提取动作曲线。 在离线阶段,系统提取预处理后的幅值和相位特征,将这两个特征合并为动作曲线的特征并利用机器学习方法训练分类器。 系统的在线阶段是利用训练完成的分类器对实时CSI 信号进行动作分类,最终完成手势识别。
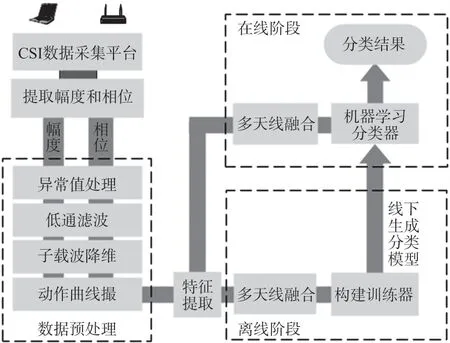
图2 人体动作识别系统框图
1.1 异常值处理
系统先对采集到的信号进行异常值处理,异常数据定义为其与全部数据均值差的绝对值大于其三倍的标准差。 检测到异常数据后,系统用全部数据的均值替换异常数据。 如式(1):

式中:Vafter为异常值处理后的数据,Vbefore为异常值处理前的数据,u为异常值处理前全部数据的均值,std为异常值处理前Vbefore的标准差。
1.2 低通滤波
低通滤波目的是对信号进行噪声处理,移除高频噪声并保留低频动作的数据。 本系统采用频率响应曲线最平滑的二阶巴特沃兹低通滤波器(Butterworth Low-pass Filter)对信号进行低通滤波。 二阶巴特沃兹滤波器的传递函数 由式(2)给出:
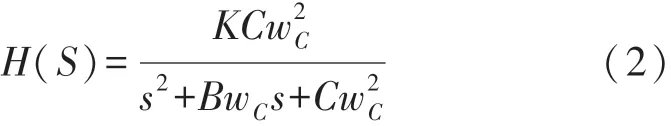
式中:K为常数,B,C为相应的系数,wC为截止频率,其中wC=2πf/FS,FS表示采样频率,即CSI 数据包发送速率。 本文采用Octave 的buttord 函数实现巴特沃兹低通滤波器,函数如式(3)所示。
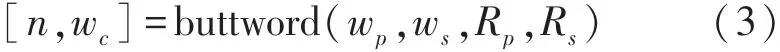
由于人体动作频率一般为0~5 Hz,所以本文设置通带截止频率wp为5 Hz,阻带截止频率ws为10 Hz,通带最大衰减Rp为3 dB,阻带最大衰减Rs为40 dB。
图3 中为一个子载波滤波前后的波形曲线,虚线表示低通滤波前的CSI 幅度,实线表示经过处理后的曲线。 由图3 可以看到滤波后曲线消除了锯齿,但保留了动作变化数据。
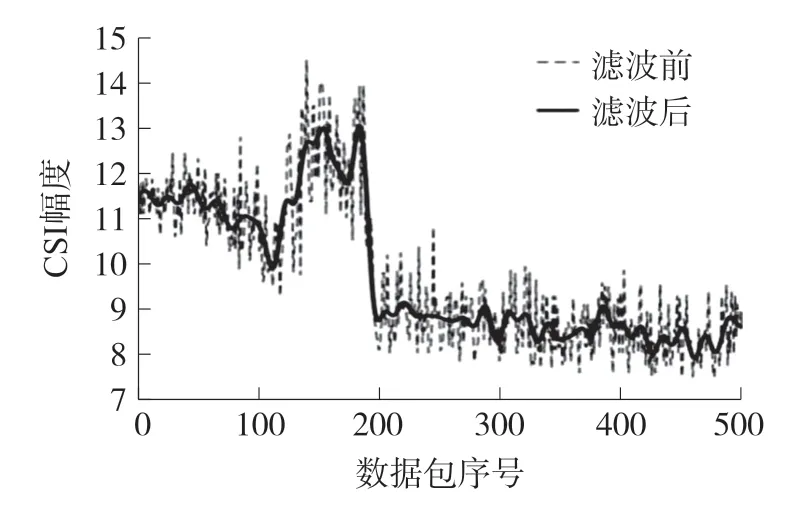
图3 低通滤波前后CSI 幅度波形对比图
1.3 子载波降维
系统采集到的CSI 数据包含有30 个子载波,如果直接使用30 个子载波的幅值和相位进行机器学习训练,会增加数据处理的复杂度和冗余度。 因此,我们首先观察同一次手势动作下5 个不同子载波呈现的波形,如图4。

图4 同一动作的不同子载波幅度波形
由图4 可以看出这五个子载波在同一次手势动作下呈现相似的变化趋势,具有极大的相关性。 因此,可以利用PCA 方法分析CSI 子载波的主要成分[12],然后选择最具有代表性的一个或者多个子载波分量。
处理结果如图5 所示,可以看到第一个特征就贡献了超过98%的数据信息,表明了30 个子载波之间确实存在极大的数据冗余。 在此选取PCA 第一个特征作为代表进行后续的处理,如图6 所示。
研究表明还有其他方法能够降低CSI 数据的复杂度,但使用PCA 有两个主要的优点:其一,使用PCA 能够明显看到每个特征分量对当前数据的贡献程度,判断数据是否存在冗余,从而选择对数据贡献大的特征作为代表;其二,PCA 可以在降维的同时消除CSI 子载波不相关的噪声分量。
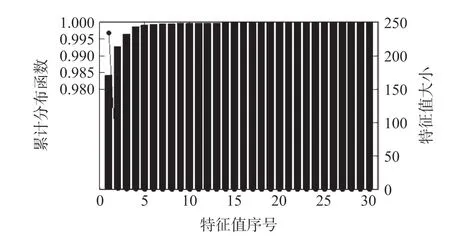
图5 主成分分析
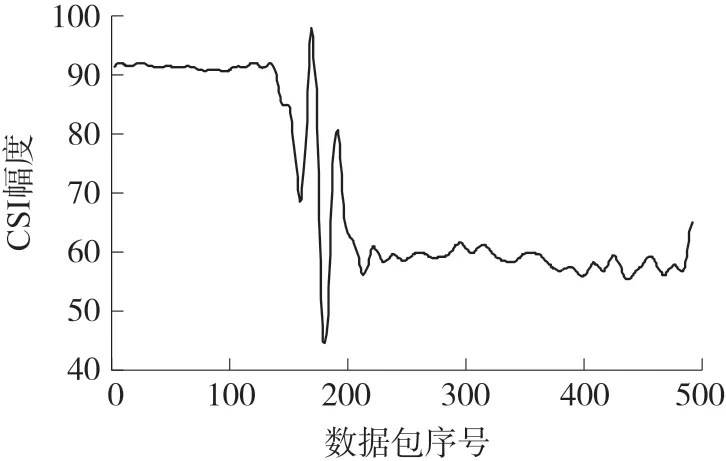
图6 经过PCA 后的CSI 数据图
1.4 动作曲线提取
对数据进行降维之后,需要从中提取动作曲线并进行离线训练,因而需要确定CSI 信号曲线中动作的起始点和结束点。 本文设计了一个从CSI 信号曲线中确定动作起点和终点的方法,主要步骤如下所示:

动作曲线提取
E为指定时间段内CSI 信号的总能量,如式(4)。
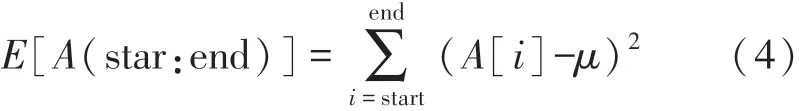
式中:μ可以由式(5)获得。
由于CSI 曲线只有在人体发生手势动作情况下才会有明显波动,因此可以利用这一点确定手势动作的起始时间和结束时间。 本文采用滑动窗口的方法计算窗口内的CSI 数据方差,作为这个时间段CSI 数据的波动程度,公式如下:

式中:A表示输入的CSI 数据,μ表示滑动窗口内数据的均值;win 为滑动窗口的长度;step 为窗口滑动步长;j为滑动窗口序号,Wj为第j个滑动窗口的方差。 滑动窗口过长、步长过大就无法体现曲线局部的方差信息,窗口过短、步长太小又会增加数据复杂度。 经过数据分析,本文在实验中设定win =10,step =1。 图7 展示了CSI 数据经过滑动窗口计算方差后的数据。
从图7 处理后的波形曲线可以看出,非动作时间段的CSI 幅度波动平缓,导致其滑动窗口内计算的方差值较小。 动作时间段的CSI 幅度波动较大,其滑动窗口内计算的方差值就较大。 通过计算滑动区间的方差有效区分了非动作时间段和动作时间段的曲线。 接下来需要更进一步确定动作时间的起始位置和结束位置,从而提取出动作曲线。
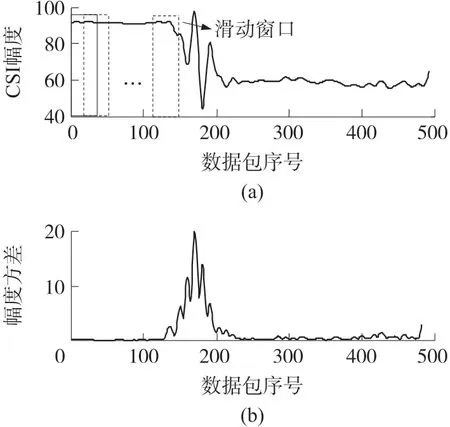
图7 滑动窗口计算CSI 幅度方差
首先获取滑动窗口处理后的CSI 方差曲线,利用差分法获取曲线的峰值点与谷值点。 然后,根据方差大小设定阈值T,将大于T的峰值点筛选出来。最后将第一个峰值点左边邻近的谷值点作为动作曲线的起始点,将最后一个峰值点右边邻近的谷值点作为动作曲线的结束点。 这样就截取到了一个动作曲线。
图8 显示了利用上述方法检测到的动作曲线的起始点和结束点。 由于实验中CSI 数据接收的速率为100 个/s,所以图8 中横坐标对应的时间范围为0~5 s。 图8 所显示的CSI 方差曲线对应本实验中只进行一次动作的情况,但从图8 的方差曲线中可以看到截取到了两个动作。 根据实际经验可知,人体手势动作的时间范围一般为0.5 s~2.0 s,而噪声的持续时间很短并且能量E很小,因此将截取到的第一个动作曲线视为实际的动作,另一个动作则为噪声曲线。 为过滤掉噪声曲线,文中设定时间阈值和能量阈值:Tmin=0.5 s,Tmax=2 s,Emin=50。 如果起始点和结束点之间的时间差为0.5 s ~2.0 s 并且曲线的能量值大于50,就认为是动作曲线,否则就判断为噪声曲线。
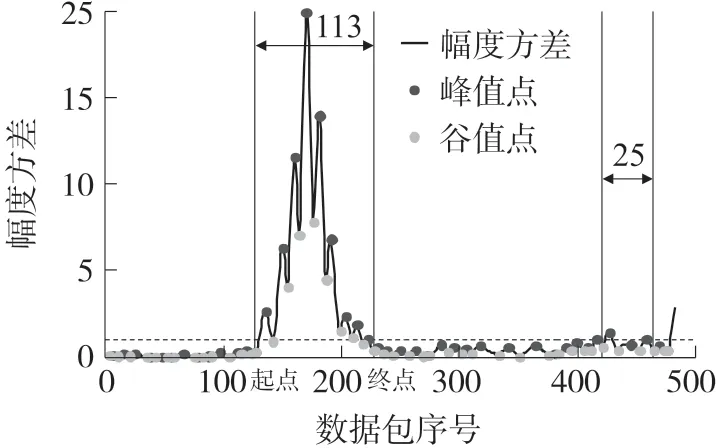
图8 检测CSI 幅度动作数据起点和终点图
将上述幅度的处理方法同样应用于相位,可提取出幅度和相位的动作曲线,如图9 所示。

图9 CSI 幅度和相位的动作曲线图
从上图可以看出幅值和相位截取的动作曲线起始点以及结束点有偏差。 为了解决这个问题,本文分别从多个天线对的CSI 幅度和相位曲线来提取动作的起点和终点,其中动作曲线起点为:
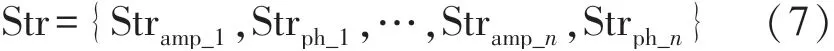
Stramp_n表示第n对天线幅度曲线的动作起点,Strph_n表示第n 对天线相位曲线的动作起点。 动作曲线终点为:
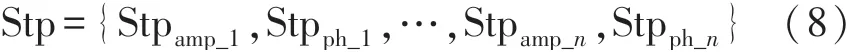
Stpamp_n表示第n对天线幅值曲线的动作终点,Stpph_n表示第n对天线相位曲线的动作终点。 然后将提取的动作曲线取交集,即最右的动作起始点Strfinal=max(Str) 和最左的动作结束点Strfinal=min(Stp)作为最后的动作曲线的起始点和结束点。
1.5 特征提取
根据动作曲线提取方法得到的动作曲线由于不同动作之间长度不一致,无法直接用提取到的动作曲线来进行动作识别。 因此本文通过提取曲线的特征值来解决这个问题。 本文分别计算了动作曲线幅值和相位的均值(Mean)、标准差(STD,Standard Deviation)、中位数绝对偏差(MAD,Median Absolute Deviation)、最大值(Max)、极差(Range)、四分位距(IQR,Interquartile Range)、峰态系数(Kurtosis)和偏态系数(Skewness),并将以上参数作为特征值进行训练。
将分别得到的幅值和相位特征值进行合并,作为一组天线获取到的CSI 信号的特征值,如式(9):
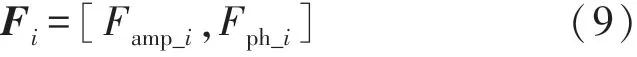
多组天线获取到的CSI 特征值为:
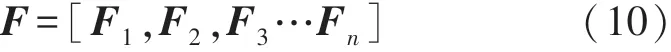
在实验中,本文采用z-score 标准化的方法对特征值进行了归一化,避免特征值单位不统一对实验结果造成的影响,如式(11):

式中:X为原始数据,u为均值,s为标准差。
2 实验设计
在实验部分本文设计了六个动作,如图10 所示。

图10 实验动作设计
六个动作分别是单手向前、单手向后、单手向左、单手向右、单手向上和单手向下。 实验中对每个动作分别采集了100 个测试样本和100 个训练样本。 样本采集时数据包接收的速率为100 个/s。 实验的硬件设备是两台配置了Inter 5300 网卡的笔记本电脑,分别用于接收和发射,WiFi 信号的中心频率为2.4 GHz。
实验场地为空旷的会议室,分别设计了近距离(2 m)和远距离(5 m)两种场景下的手势识别实验,如图11 所示。

图11 实验场景图
3 实验结果分析
3.1 特征选择的影响
在实验中,分别使用幅值特征、相位特征、幅值和相位特征结合三种方式来观察特征值选取对手势识别精确度造成的影响。 为了避免实验的偶然性,分别使用K 最邻近算法(KNN)、朴素贝叶斯(GNB)、支持向量机(SVM)和随机森林(RF)这四种机器学习算法对手势识别的准确率进行了计算,如下图12 所示。
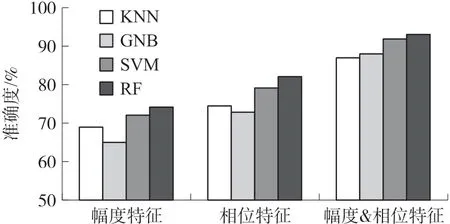
图12 不同特征组合的动作识别精度
从上图中可以发现相位特征识别的准确率高于幅值特征的手势识别。 这说明相位确实对周围环境的变化更加敏感。 幅值和相位组合的特征值在不同的机器学习算法下准确率都是最高的,由此证明了本文提出的幅值和相位结合的方式是可行的,能够有效提升基于WiFi 信号手势识别的准确度。
3.2 距离的影响
实验中,我们分别在近距离(2 m)和远距离(5 m)条件下,采用上述的四种机器学习算法对手势识别特征值进行处理,其结果如图13 所示。
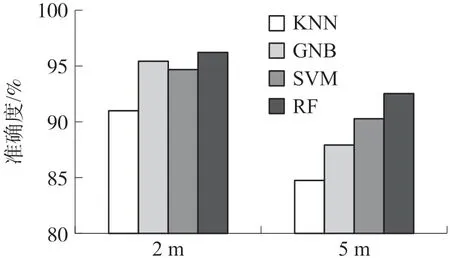
图13 不同距离场景的动作识别精度
由图13 可知,本文提出的算法在不同距离的情况下准确率有所不同。 近距离时,由于信号传播路径短,引入的噪声小,所以具有较高的准确率,RF 算法更是能够达到96%的准确率,远高于文献[6]提到的WiGest 在单AP 情况下87.5%的准确率,并且与其三个AP 情况下的准确率96%相当。 远距离时,传播距离远导致信号引入的噪声变多,使得手势识别准确率下降,但最高的准确率也有93%。 这表明本文所设计的系统能够在不同距离下对手势进行识别,并且具有较大的识别范围。
我们也给出了RF 算法在远距离下的动作识别精度的混淆矩阵,如图14 所示。
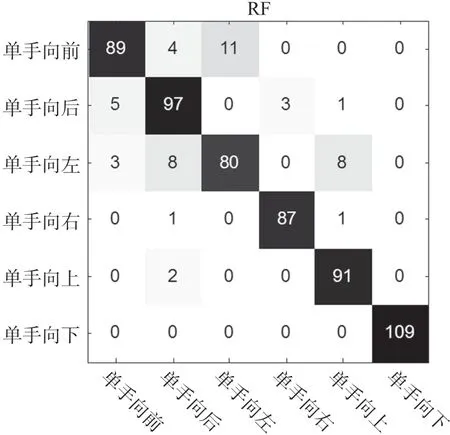
图14 远距离场景RF 算法的动作识别混淆矩阵
3.3 干扰的影响
为了进一步验证算法的有效性,考虑算法在环境中有其他人员干扰的情况下,是否能够对手势识别进行准确的分类。 因此,我们增加了实验场景中存在其他人在室内随意走动时的动作分类效果,结果如图15 所示。
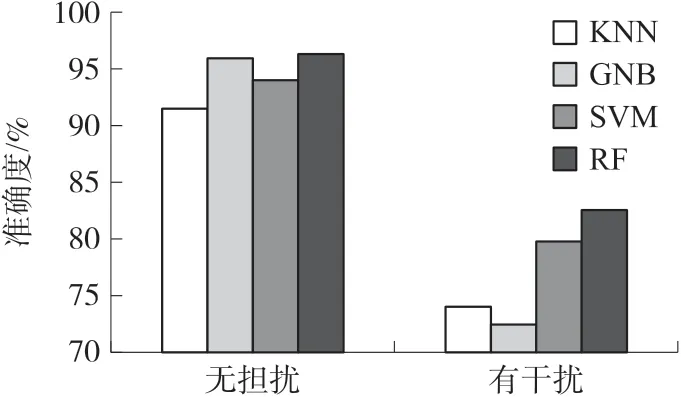
图15 有/无人员干扰动情况下分类精度
可以看到在有人员活动的情况下,算法分类的准确度有明显的下降,但最好的准确率仍然有83%。 这表明本文提出的算法具有一定的抗干扰能力,但无法完全避免其他人员活动对系统造成的影响。 如何解决周围人员活动对算法精确度造成的影响是未来研究的一个重要方向。
4 总结
本文详细介绍了基于信道状态信息CSI 幅值和相位结合的手势识别。 首先,利用PCA 对采集到的CSI 数据降低数据的复杂度;然后设计了一种利用滑动窗口计算CSI 方差的方法确定动作的起始点和结束点,以获取动作曲线;最后提取CSI 幅值和相位特征进行了多种机器学习算法的训练,实现了不同手势动作的识别,并在不同距离场景和有无人员干扰场景下分别验证了算法的有效性。 本文算法近距离情况下的准确率能够达到96%,远距离情况下能达到92%。
在未来的工作中,将着重研究如何在有其他人员干扰的情况下提高动作识别的准确度。 同时尝试将深度学习的方法应用到基于CSI 的手势识别,以实现更多复杂的手势分类。

