含风光柴蓄的电动汽车充电站容量优化配置方法

（西安理工大学自动化与信息工程学院，陕西西安710048）

我国海岛众多，海岸线长，由于远离大陆导致其无法与大电网相连。已开发的海岛都是以柴油机为主要发电设施。柴油机发电需要运输大量柴油，浪费人力、物力、财力，而且单一发电形式可靠性低，环境污染严重。但是，海岛地区可再生资源丰富，比如风能、太阳能、潮汐能等[1-4]。由于可再生能源受天气影响较大，存在较大的波动性，需要储能装置来平抑可再生能源的波动性[5]。于是通过构建多能源复合的微电网来为电动汽车充电成为了一种绿色低碳且能平抑可再生能源波动的最优选择。

国内外已经有部分文献对这种多能源复合微电网进行了研究。文献[6-8]介绍了国内外一些已经建设完成并且投入使用的光伏发电电动汽车充电站及其运行策略。文献[9]构建了一个考虑分布式光伏发电、风力发电、储能锂电池组、柴油机发电的微电网互联运行优化模型。提出了分时优化调度与实时定功率控制相结合的微电网互联运行控制策略，通过对下一时段光伏与风机发电功率进行预测，使用最优潮流算法以两微电网发电量最小为目标，实现多个微电网系统的互联运行，完成能源互补。文献[10]针对新能源发电的波动性，提出基于多代理技术的微网社区双阶段能量调度策略，不仅考虑了日前调度，而且考虑了日内实时调度，并运用粒子群算法求解最优日前调度计划。文献[11]提出普适性的多时间尺度微电网能量管理优化调度方案，包括日前预测和日内优化调度两部分。文献[12]在考虑峰谷电价的基础上，构建了基于电量电价弹性矩阵的用户多时段电价响应模型，并提出分时电价下储能充放电策略及微网优化运行策略。

以上研究成果对多能源复合微电网的运行提供了理论依据，但多考虑的是城市地区的情况，没有考虑到一些可再生能源丰富地区的情况，例如大部分的海岛地区。

综上所述，本文首先给出了多能源复合电动汽车充电站的基本构成，分析了各部分模块的功能。然后以系统投资运营成本最小和可再生能源利用率最大为优化目标构建数学模型，用储能电池组吸收多余的光伏和风力发电电量。考虑柴油发电功率约束、光伏和风机发电系统功率约束、储能系统约束、系统功率平衡约束等约束条件，运用NSGA-II算法对算例进行求解，通过对不同优化模型的结果分析以及不同情况下各模块的功率平衡分析和电量平衡分析验证了所建数学模型的有效性。

1 电动汽车充电站概述

1.1 系统结构

本文所研究的多能源复合电动汽车充电站主要由光伏阵列、风力发电机组、柴油发电机组、储能系统、变流模块、中央控制器组成。充电站系统结构图如图1所示。

图1 充电站系统结构图Fig.1 Charging station system structure drawing

1.2 系统各部分功能

1）可再生能源发电系统由大规模光伏板串、并联组成，光伏板吸收太阳能并转化为电能经输电线输送到充电站。

2）储能系统在光伏以及风力发电量大的时候，将多余电量存储在储能电池中，在发电量不足的时候释放储存的电量，起到了平抑光伏和风机波动的作用，并提高系统可再生能源的利用率。

3）柴油发电机在多能源复合发电系统中作为平抑可再生能源波动的主要方式。

4）变流器模块作为光伏电池阵列、风力发电机组、柴油发电机组、水轮机组和电动汽车充电系统中的变流单元。

5）中央控制器调控各部分的能源流动，监测充电站是否安全运行，完成系统的监测与控制功能。

1.3 系统能源交换策略

光伏发电和风力发电的首要目标是对电动汽车进行充电。如果二者的发电量大于站内电动汽车需求电量，则开始对储能电池组进行充电；如果二者的发电量小于站内电动汽车需求电量，则由储能电池组进行补充，如果仍不能满足需求则启动柴油发电机进行发电为电动汽车充电。

由系统功率的平衡关系可知，储能电池组处于充电状态时，如果光伏电池组的发电功率和风机组的发电功率之和小于储能电池组充电功率、电动汽车充电功率、充电站常规负荷功率之和，即

那么此时需要柴油机进行能量补充，柴油机此时功率Pdgi为

式中：Pevi为电动汽车在i时段的充电总功率；Pbi为常规负荷在i时段的用电功率；Psei为储能系统在i时段的用电功率；Ppvi为光伏电池组的发电功率，由光伏板数量、光伏板倾角、光照强度决定；Pwdi为风力发电机组的发电功率，在优化过程中根据以往数据以及未来气象数据进行预测；ηdd为DC-DC变流模块效率；ηad为AC-DC变流模块效率。

当光伏发电功率和风机组的发电功率之和大于或等于储能电池组充电功率、电动汽车用电功率、常规负荷功率之和的时候，即

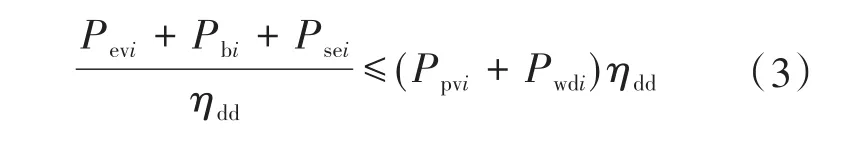
此时则不需要柴油机进行发电。柴油机此刻的功率为0。调整储能系统的功率使储存电量尽可能的大，最大限度地利用光伏电池组和风机组发的电，即

当储能系统处于放电状态时，如果此时光伏电池组的发电功率和风机组的发电功率以及储能系统的放电功率之和小于电动汽车充电功率和常规负荷用电功率之和时，即

此时可再生能源发电系统不能满足系统用电需求，需要柴油机工作发电，且柴油机此刻的发电功率为

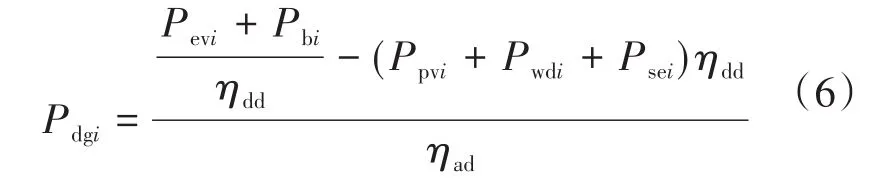
如果此时光伏电池组的发电功率和风机组的发电功率以及储能系统的放电功率之和等于电动汽车充电功率和常规负荷用电功率之和，则无需启动柴油发电机组。此时储能系统的功率如下式所示：

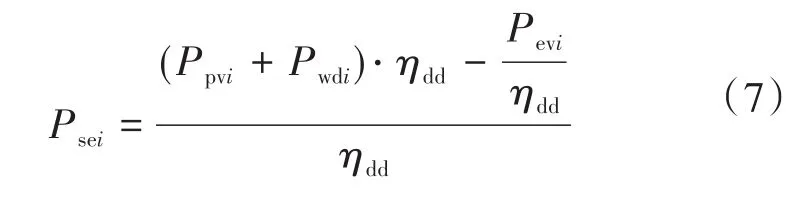
通过对以往电动汽车的停放数据[13]进行分析可以得到电动汽车的充电时间规律以及电量需求，即

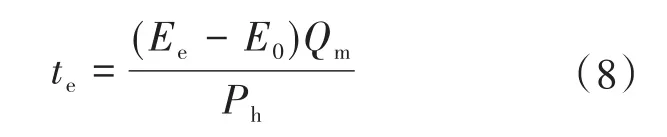
式中：te为单台电动汽车的充电时间；Ee为电动汽车完成充电时的电量值；E0为电动汽车的初始电量值；Qm为电动汽车蓄电池的额定容量；Ph为电动汽车充电功率（此处取恒功率充电）。

2 充电站容量优化配置模型

2.1 目标函数

2.1.1 系统投资运营成本

在整个充电站的能源结构中，系统的总体建设成本是各模块的购买费用。可再生能源发电一旦建好就不需要另外的购电费用，所以充电站的主要运营成本是柴油机的发电费用及各模块维护费用。系统的投资运营成本可表示为

式中：Cm为系统总投资运营成本；Cpv，Cwd，Cdg，Cse，Cdc，Cfc分别为光伏模块投资运营成本、风力发电机组投资运营成本、柴油发电机组投资运营成本、储能系统投资运营成本、系统变流模块投资运营成本、柴油机发电费用。

系统各模块投资运营成本如下：

1）光伏模块投资运营成本为

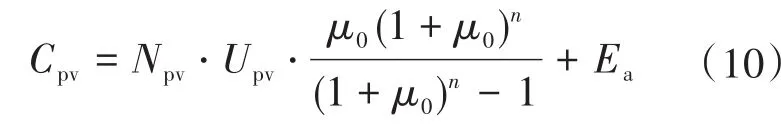
式中：Npv为光伏板个数；Upv为光伏板单价；μ0为系统折现率；n为系统运营时长；Ea为系统的维护成本。

2）风力发电机组投资运营成本为

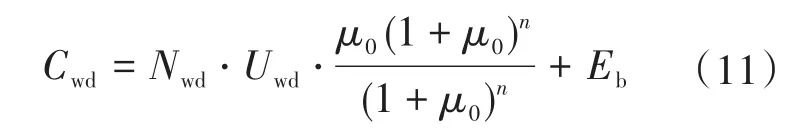
式中：Nwd为风力发电机台数；Uwd为风力发电机单价；Eb为风力发电机组维护费用。

3）柴油发电机组投资运营成本为

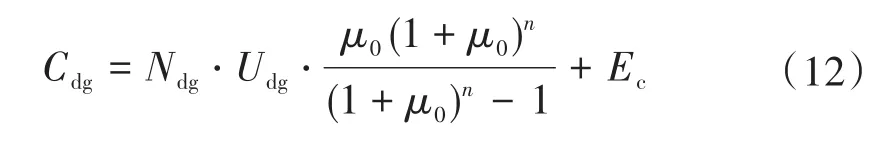
式中：Ndg为柴油发电机台数；Udg为单台柴油发电机价格；Ec为柴油发电机组维护费用。

4）储能系统投资运营成本为

式中：Nse为储能电池组个数；Use为单个储能电池组的价格；Ed为储能系统维护费用。

5）系统变流模块投资运营成本为

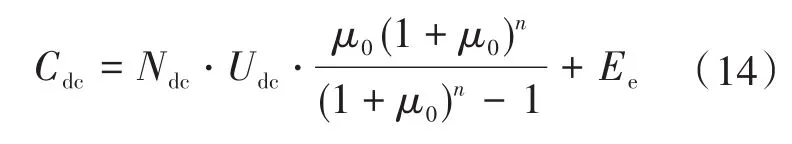
式中：Ndc为变流模块个数；Udc为单个变流模块的价格；Ee为变流模块维护费用。

6）柴油发电机油耗成本为

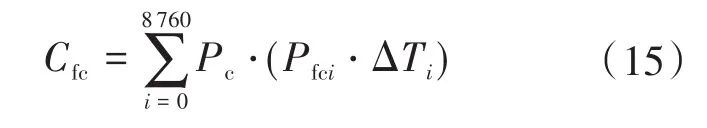
式中：Pc为柴油机单位油耗费用，元（/kW·h）；Pfci为i时段柴油发电机总功率；ΔTi为i时段的时长。

在光伏以及风力发电量大的时候，将多余电量存储在储能电池中；在发电量不足的时候释放储存的电量，起到了平抑光伏和风机波动的作用，提高了系统可再生能源的利用率。

2.1.2 可再生能源利用率

要想真正实现绿色环保，就需要最大限度地利用可再生能源，即

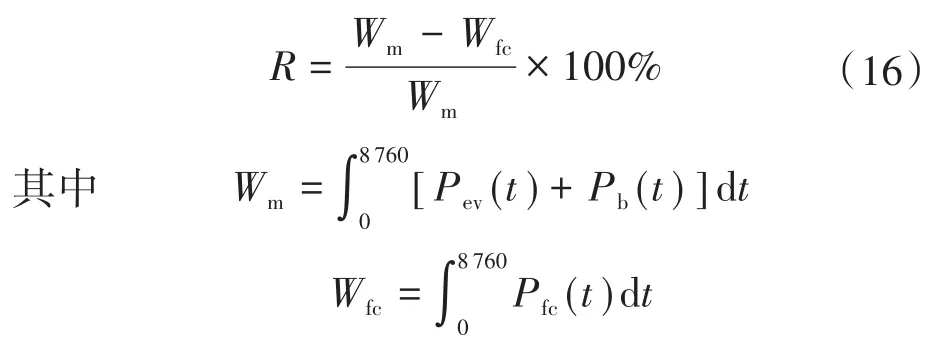
式中：R为可再生能源利用率；Wm为系统的年用电量；Wfc为柴油发电系统的年发电量；Pev(t)为t时刻电动汽车充电功率；Pb(t)为系统t时刻充电站常规负荷用电功率；Pfc(t)为t时刻柴油机的发电功率。

2.2 模型的约束条件

1）柴油机发电功率约束为

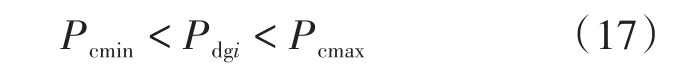
柴油发电机一般都有一个最大运行功率和最小运行功率限制，如果超出范围很可能会损坏。

2）光伏风力发电机组约束。光伏发电受光照强度（对于特定地区光照强度是规律的）、光伏阵列倾角α、光伏电池板数量Npv等条件影响，而风力发电机组则受风力强度、风机组功率Pwd、风力发电机组数量Nwd等条件的影响。具体约束条件为

式（18）中各条件上限由具体情况决定。

3）储能电池组约束。储能电池组一般从出厂就标注了最佳充电范围，其充电功率约束为

4）系统功率平衡分析。整个充电站的各个模块满足功率平衡条件，当储能电池组处于充电状态时，满足：

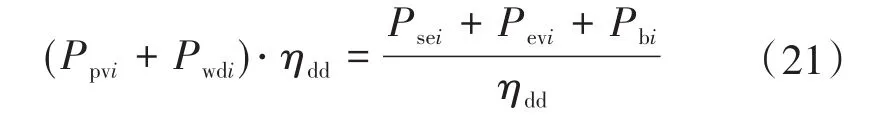
当储能电池组处于放电状态时，满足：

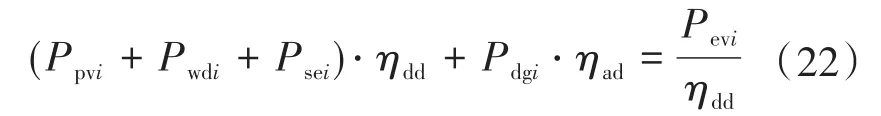
3 模型求解

分析所构建的模型可知，该模型是典型的多目标优化问题。拟采用带精英策略的非支配排序遗传算法（non-dominated sorting genetic algorithms-II，NSGA-II）进行求解。NSGA-II采用快速非支配排序，该方法的时间复杂度O(n)为O(MN2)，其中M为优化对象的数量，N为种群大小。引入精英策略，使种群中的个体多样性得到保留。采用拥挤度和拥挤度比较算子，不但克服了NSGA中需要人为指定共享参数的缺陷，而且将其作为种群中个体间的比较标准，使得准Pareto域中的个体能均匀地扩展到整个Pareto域，保证了种群的多样性[14]。该模型的计算步骤如下：

1）计算系统各模块的建设运营费用，可由式（10）～式（14）求出。

2）根据历史数据以及未来天气情况以及式（18）的约束条件计算光伏发电系统和风力发电系统的发电。求出储能系统的充放电功率，在式（19）和式（20）的约束条件下求出储能系统的充放电功率。

3）根据汽车行为规律计算出汽车用电需求，根据系统功率平衡约束条件，求出柴油机发电量及发电费用。

4）计算目标函数之系统投资运营成本，由各模块建设维护费用和柴油机发电费用结合式（9）～式（15）可求出。

5）计算目标函数之可再生能源利用率，根据各个模块发电量，结合式（16）可以求出。

图2为NSGA-II算法求解流程图。

图2 NSGA-II算法求解流程图Fig.2 Flow chart of solving NSGA-II algorithm

4 充电站容量优化配置算例分析

4.1 研究对象及基础数据

本模型中以中国南部某地区海岛作为研究对象，通过容量优化配置，根据系统的目标函数和各约束条件收集该地区不同月份的日照情况以及风力情况。通过数据进行优化分析，并对系统各模块功率平衡条件进行分析对比，得出最优容量配置方案。

图3为该岛屿月太阳光辐射量平均值[15]。图4为根据随机抽取的100辆电动汽车计算出的电动汽车行为规律及用电量需求。

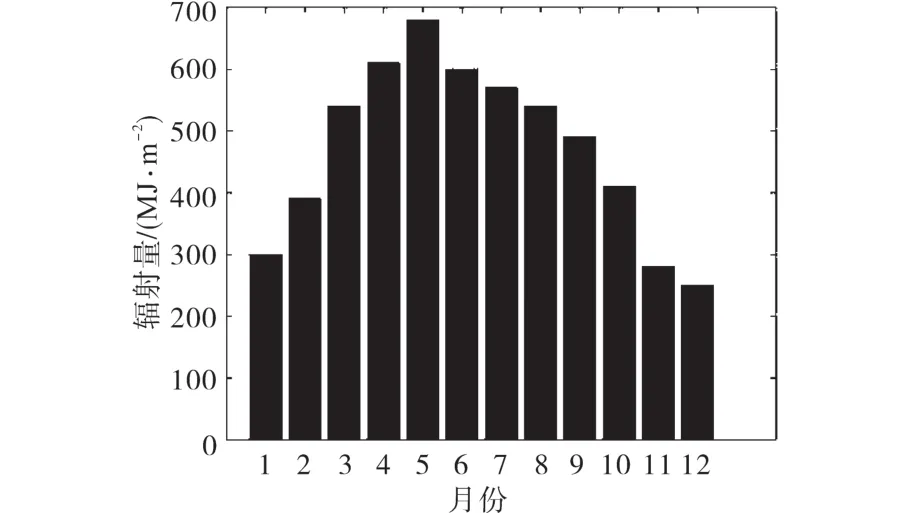
图3 辐射量平均值Fig.3 Mean dose of radiation

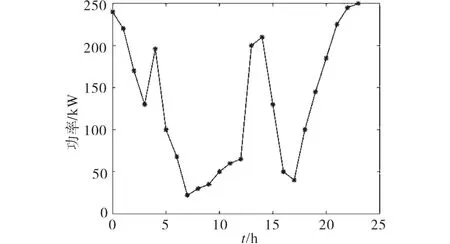
图4 电动汽车充电需求Fig.4 Demand for charging electric cars

风速不同，风力发电机组的功率也会有变化，选取图5所示两种风速下风力发电机组的功率作为基础数据[16]。

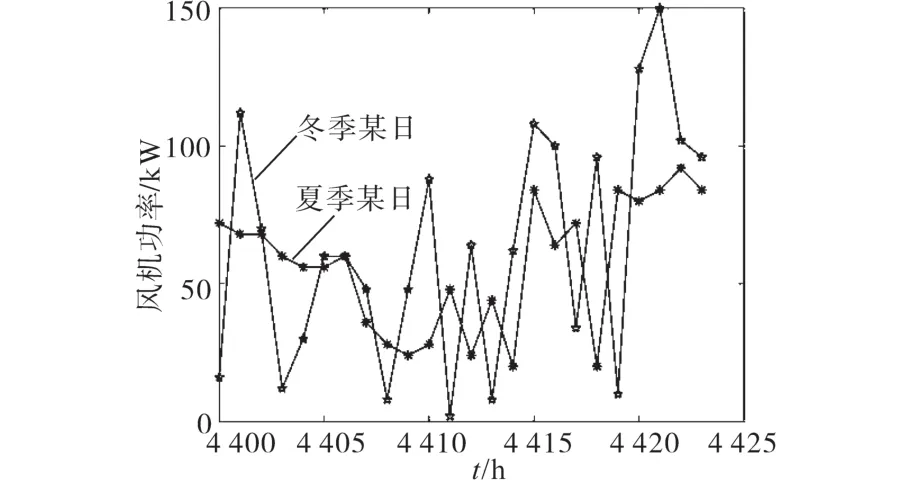
图5 两种典型情况风力发电机发电功率Fig.5 Two typical cases of wind turbine power generation

充电站在运行的时候储能系统初始荷电状态SOC（state of charge）也会对优化策略产生影响。充电站建设各模块的功率配置如表1所示。

表1 能源类型及其相关参数Tab.1 Energy types and related parameters

4.2 优化结果分析

4.2.1 最优解分析

利用Matlab软件编写NSGA-II算法对以上算例进行求解，设定种群数量为500，最大迭代次数为400，交叉率0.9，变异率0.1。Pareto最优解如图6所示。

图6 Pareto最优解分布情况Fig.6 Pareto optimal solution distribution

由图6优化结果可知，随着系统投资运营成本的提高，可再生能源利用率也在不断增加。图中的Pareto解分布范围广泛，可以为投资者提供详细的决策方案。根据所求得的Pareto解的分布情况可以寻找合适的建设方案。成本和可再生能源利用率之间是相互冲突的，如果投资者资金有限，则优先考虑成本低的优化方案；如果投资者资金充足，则从长远来看应选择可再生能源利用率高的优化方案。总之，投资者可以根据具体的需求来挖掘最优解的信息，选择一个适合的优化方案。

4.2.2 系统各组件功率分析

从Pareto最优解中选取3种优化方案进行系统功率平衡分析。方案1：可再生能源利用率为10%，成本为100万元。方案2：可再生能源利用率为30%，成本为187万元。方案3：可再生能源利用率为50%，成本为324万元。选取夏季6月某典型日、冬季12月某典型日，对系统各个组件进行功率平衡分析。3种方案下的各个模块容量配置情况如表2所示。

表2 三种典型方案容量配置情况Tab.2 Capacity configuration of three typical schemes

图7为方案1充电站功率平衡图。由图7可知，充电站内的电动汽车充电所需的能量由柴油机、光伏发电系统及风力发电系统共同提供。白天主要是光伏发电系统、柴油发电系统及风力发电系统供能；晚上主要是风力发电系统和柴油发电系统供能。

图7 方案1充电站功率平衡图Fig.7 System power balance of charging station under scheme 1

光伏发电系统和风力发电系统受天气影响较大，夏季天气炎热，太阳光强度大，光照时间长，光伏板发电量大于冬季。夏季风力强度波动性比较小，风力发电系统供能也比较稳定，冬季风力强度波动较大，风力发电系统供能不稳定[17]。此时没有为系统加入储能系统，所以系统不能平抑光伏和风力发电的波动，系统出现弃风弃光现象。

图8为方案2充电功率平衡图。由图8可以看出，当可再生能源利用率为30%的时候，充电站内建设了储能系统，在光伏发电的高峰期储能系统把多余太阳能转换为化学能储存起来，等到太阳能发电的低谷阶段，储能系统和风机发电一起为系统提供能量[18]。图中出现了负值的情况，此时储能系统开始将多余的可再生能源发电量储存起来。通过比较冬季和夏季的情况可以发现，夏季光照强、辐射量大，储能系统可以储存更多的能量。通过投建的储能系统可以明显地平抑太阳能和风能的波动，提高了可再生能源利用率。

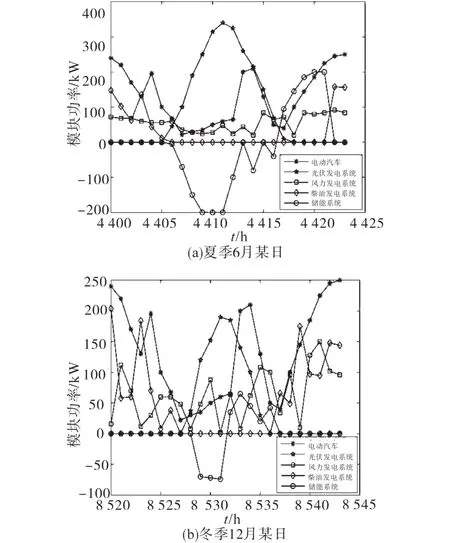
图8 方案2充电站功率平衡图Fig.8 System power balance of charging station under scheme 2

图9为方案3充电站功率平衡图。由图9可知，当可再生能源利用率为50%时系统中可再生能源就可以满足用电需求，储能系统可以持续地工作，油机发电基本处于停滞状态。

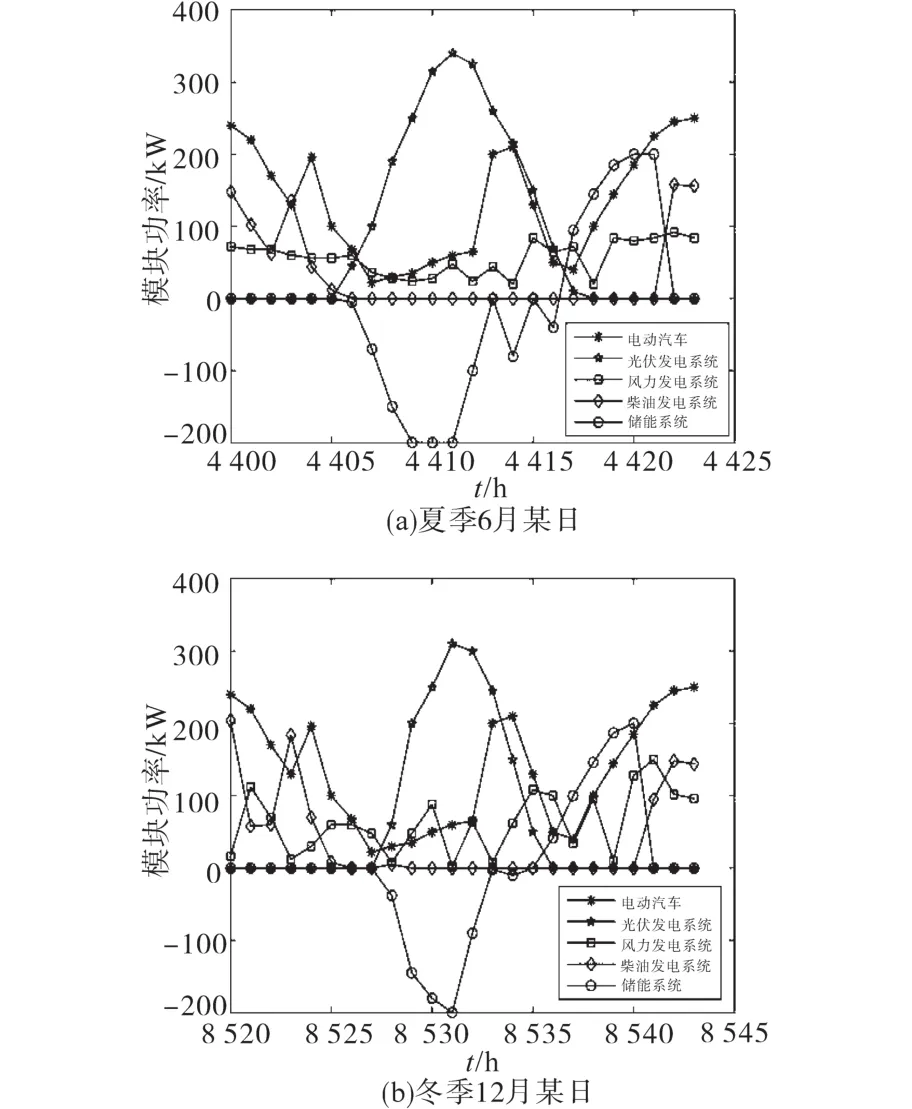
图9 方案3充电站功率平衡图Fig.9 System power balance of charging station under scheme 3

通过对以上3种情况的分析，随着可再生能源利用率的增大，光伏发电功率也在增加，系统的投资金额也随之增加。当可再生能源利用率为10%时，充电站以柴油机发电为主，所以出于投资最小化考虑，充电站不建设储能系统。

4.2.3 系统电量平衡分析

三种方案下，一年中每月电动汽车用电量、光伏发电量、风力发电量、柴油机发电量的情况分别如图10～图12所示。

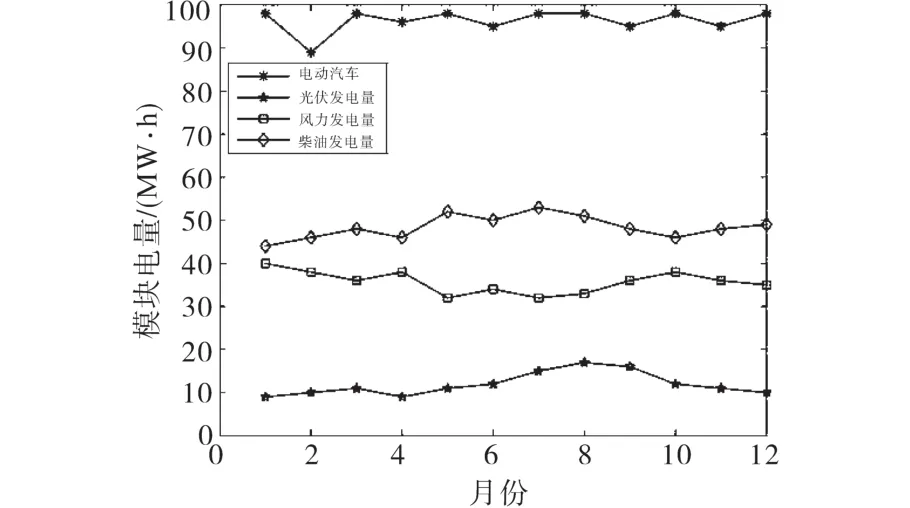
图10 方案1充电站电量平衡图Fig.10 System energy balance of charging station under scheme 1

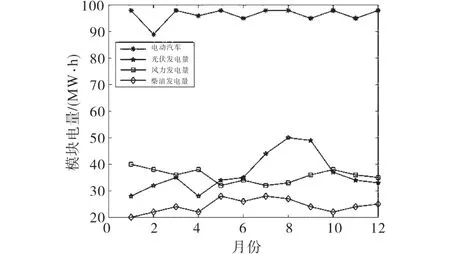
图11 方案2充电站电量平衡图Fig.11 System energy balance of charging station under scheme 2

图12 方案3充电站电量平衡图Fig.12 System energy balance of charging station under scheme 3

分析图10～图12可知，当可再生能源利用率为10%的时候，系统以柴油发电机发电为主；当系统可再生能源利用率为30%的时候，各模块基本均匀出力；当系统可再生能源利用率为50%的时候，柴油机基本停止使用，系统以可再生能源发电为主。考虑一定的系统损失，不同月份系统各模块发电量基本等于电动汽车用电量需求。在光伏发电量大的月份（如7月～10月）出现一定的弃光弃风现象，为系统配置的储能系统能在一定程度上平抑光伏和风机的波动。

5 结论

本文建立了含风、光、柴、储的多能源复合电动汽车充电站容量优化配置模型。利用某海岛已知数据作为条件，以系统投资运营成本最小和可再生能源利用率最大为优化目标，通过NSGA-II算法对算例进行求解，得到Pareto最优解，并对系统各模块进行了功率平衡分析。

根据各地区的实际情况以及投资需求选择合适的建设方案，通过对成本和可再生能源利用率进行综合分析，以及对系统各模块功率平衡分析，可以知道，所构建的目标函数以及各约束条件符合实际。选取了实际的数据信息对系统进行验证，结果符合本文的预期。所构建的优化配置模型可以为海岛地区的充电站建设提供理论和技术支持，具有实际的利用价值。

后续工作可以将系统各模块的详细损耗考虑进去，做更加精确的分析。也可以考虑将抽水储能或者潮汐能考虑在内进行规划计算。