同步发电机短路故障分析方法研究

（四川水利职业技术学院电力工程系，四川成都611133）

对于发电机来说，励磁绕组匝间出现短路故障是比较常见的[1]。通常情况下，轻微匝间短路并不会影响发电机正常运行，另外，现有匝间短路保护措施并不完善，所以不会强制要求安装励磁绕组匝间短路保护装置[2-3]。但是如果任凭短路故障继续发展，会造成一系列严重后果，例如输出无功功率减小、励磁电流增加、发电机剧烈震动等[4-7]。短路点的局部过热容易损坏转子铁心，甚至导致大轴磁化，有可能出现轴颈和轴瓦烧伤的情况，降低机组运行安全系数[8-10]。因此，开展发电机励磁绕组匝间短路故障分析方法研究具有十分重要的意义。

目前，众多研究人员已开展这方面研究。樊静等人以发电机转子绕组匝间短路后磁场变化为研究对象，利用有限元分析建立了短路程度和不对称磁场之间的关系，同时论证了磁场不对称将产生一定的电磁应力[11]。孙宇光等人基于多回路理论确定了同步发电机数学模型，在励磁电压保持不变的条件下，分析、对比了故障前后励磁电流、定子电流的谐波特征[12]。

本文在现有研究的基础上，利用场路结合算法对同步发电机短路故障进行分析并进行仿真和实验研究。

1 同步发电机多回路数学模型

多回路分析法不仅可以较好地实现电机绕组内部各回路电流、电压的分析、计算，而且能够分析气隙磁场的各种谐波。为体现一般性，文中以并联支路数为1且只有一处匝间短路的励磁绕组作为研究对象。

1.1 定子回路电压方程

励磁绕组匝间短路故障会造成相绕组内部电流失衡，所以不能以相绕组为基础单元求解定子方程，需要结合多个相绕组进行分析。

如果将定子各回路电流作为变量，那么可得到定子各回路电压方程，即

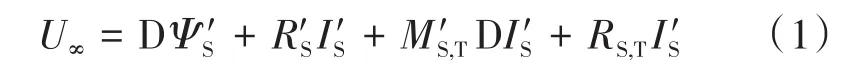
式中：U∞为电网电压，其值无穷大；D为微分算子；为磁链为电流为电阻为漏感作用变量为电阻作用变量。

1.2 励磁绕组电压方程

如果发生匝间短路故障，励磁绕组会存在2个独立回路，其中正常励磁回路的电流为if，附加回路电流为ifkL。此时励磁绕组电压方程可表示为

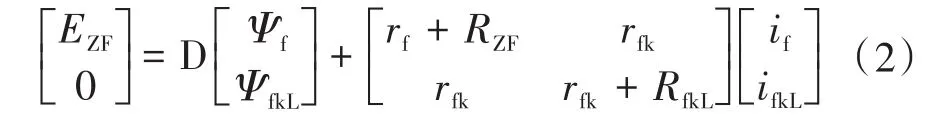
式中：Ψf为正常回路磁链；ΨfkL为故障附加回路磁链；rf为正常回路电阻；rfk为短路匝电阻；EZF为电源电动势；RZF为电源内阻；RfkL为故障附加回路过渡电阻。

1.3 阻尼绕组电压方程

由于故障气隙磁场存在不同空间谐波，如分数次谐波，文中以实际网型阻尼回路为研究对象，其电压方程可表示为

式中：Ψd,1,Ψd,2,…为阻尼回路磁链；id,1,id,2,…为阻尼回路电流；Rd为阻尼回路电阻。

1.4 状态方程

结合上述各式就可以得到定子和转子所有回路电压方程，可统一表示为

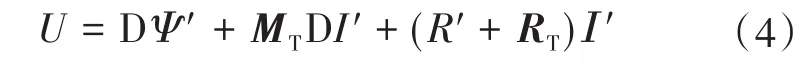
式中：U为电网电压和励磁系统电源电压；Ψ'为定子和转子各回路磁链；I'为定子和转子各回路电流；R'为回路电阻；MT，RT均为常数方阵。特别地，定、转子各回路正值电流均产生正值磁链，那么所有回路磁链可表示为

式中：M'为回路电感。

求解式（4）的前提条件是需要准确计算回路电感，尤其是发生短路故障的绕组电感。

2 电感参数计算

2.1 有限元分析

为便于计算，文中选用静态磁场进行分析，即电机内磁场始终保持恒定。为描述磁通密度Φ，可引入矢量磁位Ω，那么则有：

式中：∇为旋度算子。

以XY坐标内二维平面场为例，如果矢量磁位、电流密度仅在Z轴方向存在分量，那么发电机二维磁场的数学模型可表示为

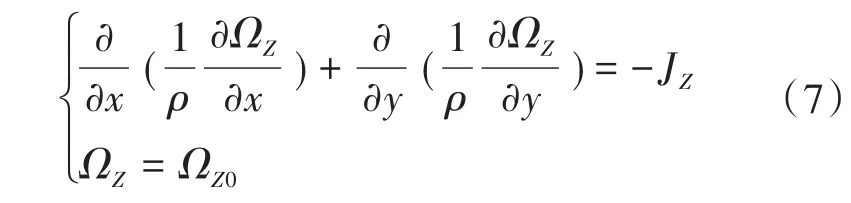
式中：ρ为磁导率；ΩZ0为边界己知值；JZ为电流密度Z轴分量。

由于空气磁导远小于铁心磁导，所以可认为穿过定子外表面的磁通为零。定子外表面处磁力线的方向与边界平行，此时矢量磁位Ω在铁心表面切线方向不会发生变化，即满足ΩZ0=0。

基于有限元分析的电感参数自动计算，关键步骤可描述如下：

1）设定计算时间和步进时间；

2）进行节点耦合，励磁电流注入；

3）判断是否空载，带负载的情况下，建立定子坐标，确定转子位置；

4）获取相位图，分别计算相电流、磁场，求解电感参数；

5）判断是否完成，若完成，则结束；否则，重复上述过程。具体流程如图1所示。

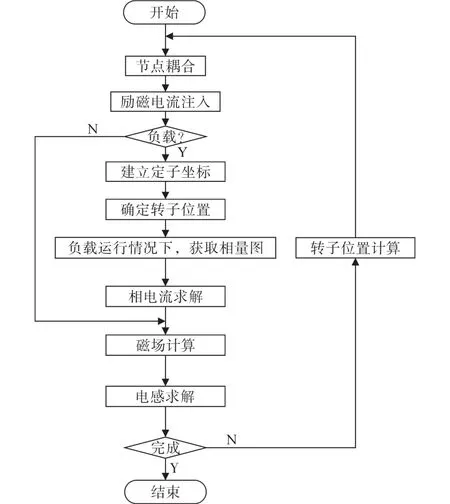
图1 电感参数计算流程Fig.1 Inductance parameter calculation process

2.2 电感参数表达式

如果仅仅选取互感参数常数项和2次谐波项，那么定子的ki支路和kj支路之间互感参数表达式可描述为

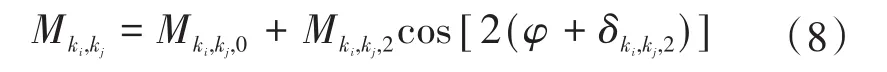
式中：Mki,kj,0为互感参数常数项；Mki,kj,2为2次谐波项幅值；δki,kj,2为2次谐波项相位；φ为转子位置角。

定子支路ki和阻尼回路dj之间互感参数表达式可描述为

式中：Mki,dj,h为互感参数幅值；δki,dj,h为互感参数相位；n为谐波次数。

定子支路ki和正常励磁回路之间的互感参数表达式可描述为

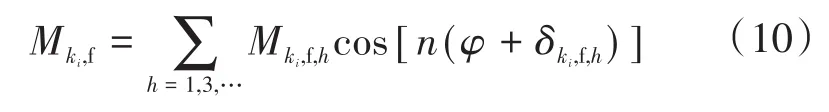
式中：Mki,f,h为互感参数幅值；δki,f,h为互感参数相位。

定子支路ki和故障励磁回路之间互感参数表达式可以描述为

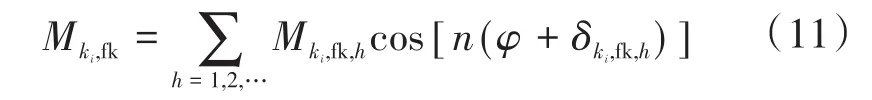
式中：Mki,fk,h为互感参数幅值；δki,fk,h为互感参数相位。

综上所述，将有限元分析所得电感参数代入回路电压方程即可实现场路结合分析。

3 仿真和实验分析

为验证所述励磁绕组匝间短路故障分析方法的可行性和有效性，参考文献[10-12]所述多回路和场路耦合仿真和实验方法，以一台凸极同步发电机作为仿真和实验平台，在联网负载情况下励磁绕组匝间发生短路故障时，基于上述“场路结合”分析方法，计算定子和转子各绕组电流。该发电机主要参数如下：额定功率12 kW，额定电压400 V，额定电流21.7 A，励磁电流22.6 A，极数4，定子并联支路2，定子槽42，励磁绕组匝数/极为94，转子阻尼条数/极为6。

为验证“场路结合”算法的有效性和优势，文中开展实验研究并与仿真数据进行比较。选用12 kW励磁绕组匝间短路专用同步发电机作为实验样机，实验过程可简要描述为：启动并调节直流调速设备，改变发电机转速，使其机端电压频率接近电网电压频率；确保样机机端电压和电网电压相序一致；确保发电机平稳入网；闭合短路开关，使励磁绕组出现匝间短路故障，记录故障数据。结果如表1所示。

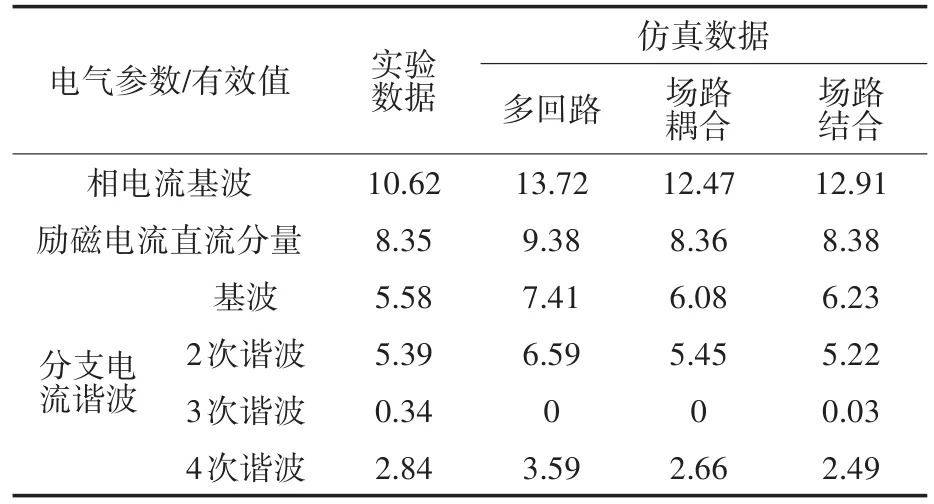
表1 数据对比Tab.1 Data comparison A

由表1可知，实验数据和仿真数据还是比较接近的，说明“场路结合”算法计算励磁绕组匝间短路故障的正确性。另外，通过对比不同仿真结果可以看出：场路结合法计算精度虽然不是最高，但是与多回路法相比，计算准确度明显提高。

综上所述，场路结合法利用有限元计算发电机电感参数，虽然计算精度低于场路耦合法，但同场路耦合法的计算结果比较接近，二者之间计算误差在工程研究可接受的范围内。另外，场路结合算法的优势在于计算速度较快。相同条件，场路耦合法完成计算耗时8 h左右，而场路结合算法仅需1 h左右，充分证明了场路结合算法在计算准确度和速度方面的优势。

4 结论

以发电机励磁绕组匝间短路故障为研究对象，重点讨论故障分析方法。在多回路分析法的基础上，通过有限元分析计算电感参数，实现场路结合分析计算。通过仿真和实验验证了所述计算方法的可行性和有效性。结果表明，场路结合计算方法在准确度和速度方面均有一定优势，可用于发电机匝间短路故障计算、分析。