基于迭代优化的多电机交叉耦合控制方法研究

李书领，段松凯，李书良

（1.河南机电职业学院电气工程学院，河南郑州451191；2.包头钢铁集团，内蒙古包头014000）

随着科学技术的发展，人类生产生活对机电设备复杂程度的需求日益提升，电机作为机电产品中的驱动设备，已被广泛应用于各个领域。利用电机实现电能与机械能的转换，具有高效、环保且可靠的优点，是目前工业生产和控制中普遍应用的驱动产品。以适应复杂工控环境和市场需求为导向，越来越多的机电产品如工业生产线、打印机、数控机床、医疗器械及工业机器人等，其控制系统都需要多电机协同控制，驱动执行机构实现预期功能。目前，多电机控制系统中存在的迟滞非线性、参数摄动及多状态变量等问题是研究的重点和难点，国内外学者对此展开广泛深入研究，以提高多电机同步控制或协同控制的精度[1-4]。

冯建修等学者[5]以玻璃纤维湿法毡生产线为研究对象，提出了基于变频器间数据传输特性和控制器特性的激光测距闭环控制策略，并说明了交流同步传动系统的实现方法。谷雨等学者[6]在相邻交叉耦合控制策略的基础上，考虑不同职能电机的功能权值，提出了加权交叉耦合的多电机同步控制算法，利用Matlab/Simulink对算法的有效性和稳定性进行了验证。李言民等学者[7]为保证多台伺服电机的同步控制精度，提出了基于模糊PID控制器的多电机交叉耦合控制方法，通过Matlab仿真实验验证了此方法对系统抗扰动的优化。上述方法通过优化控制器结构和参数提高多电机同步控制精度，但由于这些控制方法需要较大计算量，多通过仿真验证算法的性能，难以应用在实际工控环境中。

Xia Changliang等学者[8]针对两自由度机械控制平台，在传统的比例积分速度控制器基础上，利用卡尔曼滤波对速度反馈信号实时估计，降低传感器反馈信号的噪声，提高多电机同步控制精度。涂文聪和周湛清等学者[9-10]分别利用模糊动态代价函数和鲁棒控制方法实现模型预测电流或转矩控制，将现代智能控制算法思想融入控制器，可有效提高伺服电机单轴跟踪精度。樊英等学者[11]提出了基于新型趋近律和混合速度控制器的IPMSM调速系统滑模变结构控制，通过提高单轴永磁同步电机的跟踪性能来间接提高多电机同步跟踪性能。综上所述，利用提高单轴动态特性及反馈信号准确度的方法可以在一定程度上提高多电机同步控制精度，但是对于具有交叉耦合特性的机电系统，此类方法不再适用。

Shi Tingna等学者[12]简化了基于偏差耦合的控制器结构，利用速度环同步控制调节实现多电机同步性能和跟踪性能的解耦控制。为兼顾控制系统单轴跟踪性能和多轴同步性能，耿强等学者[13]针对传统偏差耦合多电机同步控制方法，将多电机系统运行过程进行分段化处理，提出了基于线性系统校正原理的改进型偏差耦合控制结构，根据分段控制需求设计控制器输出选择函数，通过仿真和试验验证了所提方法的有效性和可行性。以上方法针对实际被控对象，进行数学建模和控制器优化，能够较好地解决多电机同步控制精度的问题，但是在试验过程中需要进行大量的在线计算，给控制器带来了较大的运算负担，在一定程度上占用了控制器在其他方面的运算能力。

为了有效提升多电机交叉耦合控制系统的动态性能，降低控制器运算负载，提高算法实现可行性和普适性，本文提出一种基于迭代优化的多电机交叉耦合控制方法，针对被控对象数学模型及输入指令跟踪轨迹，设计合理的前馈控制器结构，并对前馈控制器的参数迭代优化，利用前馈控制器的有效补偿提升被控对象的多轴交叉耦合控制性能，最后，通过仿真和试验验证所提算法的正确性和有效性。

1 前馈控制器结构设计

针对含有控制器、旋转伺服电机和滚珠丝杠的机电系统，建立其数学模型，图1为机电控制系统的控制框图。

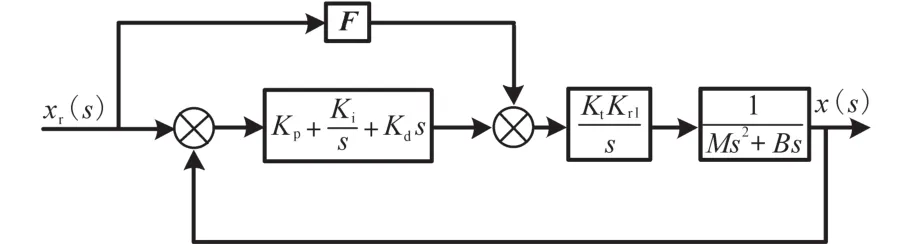
图1 典型机电系统控制框图Fig.1 Control block diagram of typical electromechanical system

图1中，控制环节采用传统的PID控制器，由于机械系统需要将旋转伺服电机的旋转运动转换为直线运动，因此利用联轴器和滚珠丝杠实现运动形式转换。针对图1的典型机电系统控制功能框图，在忽略前馈补偿环节的条件下，系统传递函数为

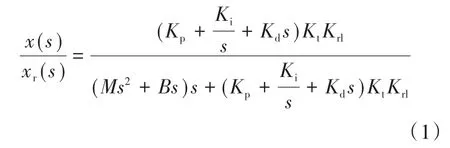
式中：x（s）为机电系统的输出位移；xr（s）为系统位置指令；Kp，Ki，Kd分别为PID控制器的比例、积分和微分系数；Kt为旋转伺服电机的转矩系数；Krl为机械平台旋转运动与直线运动的转换系数，其与联轴器刚度、滚珠丝杠参数有关；M为滚珠丝杠和移动平台在工作过程中的等效质量；B为机械平台在平行移动时的阻尼系数。

根据式（1）所示的系统传递函数，在考虑传动环节的情况下，系统含有高阶特性，在单轴运动控制过程中，常利用前馈控制器对系统特性进行补偿，实现响应快、精度高的动态性能要求。对于两轴或多轴机电系统，由于不同自由度工件台的质量相互耦合，其某一自由度工件台的等效质量随运动过程呈慢时变特性，因此针对多自由度机电系统交叉耦合问题，设计合理的前馈控制器对系统交叉耦合特性进行补偿，是提高系统动态性能的关键。

前馈控制器的设计主要包括前馈控制器结构设计和参数优化。其设计的核心是利用前馈控制器结构和参数优化实现对被控对象数学模型的逆等效。在理想状态下，若前馈控制器F能够与被控对象数学模型的逆等效，则系统在无控制器作用下也可实现对输入指令轨迹的准确跟踪。考虑到式（1）所示的系统传递函数，本文采用基于连续指令轨迹的前馈控制器，其数学表达为

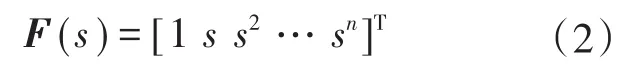
式中：F（s）为前馈控制器结构；s为对指令轨迹的微分；n为指令轨迹微分的阶数。

则前馈控制器输出ufo为

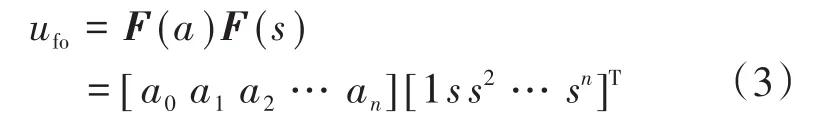
式中：F（a）中元素a0，a1，a2，…，an为前馈控制器对应参数配置。

综上，根据前馈控制器的参数和指令轨迹可以确定前馈控制器补偿量，与系统控制器输出共同确定控制率输出，实现对伺服电机的控制调节作用。以两自由度平台为研究对象，在考虑系统交叉耦合特性影响下，图2为系统交叉耦合前馈控制器结构原理，其中单轴前馈控制器用来拟合本系统模型的逆，耦合前馈控制器负责解耦其余自由度系统对本系统的影响，在此基础上需确定前馈控制器中的参数以及参数的迭代优化方法，利用准确高效的参数优化方法实现系统动态性能的提升。

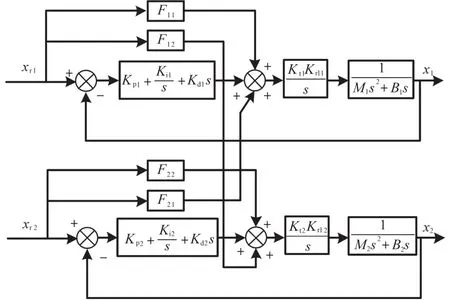
图2 交叉耦合前馈控制器结构原理图Fig.2 Structural schematic diagram of crosscoupled feedforward controller

2 迭代优化控制策略

本文采用基于连续指令轨迹的前馈控制器结构，根据前馈控制器结构，其传递函数中不含有极点，若能够保证其前馈控制量输出有界，则可确定此前馈控制器自身稳定，进而保证系统稳定性。根据图1可确定系统单轴跟踪误差的表达式如下：

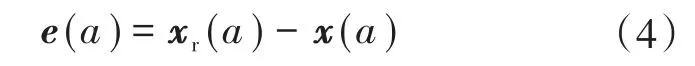
式中：xr（a）为输入指令轨迹；x（a）为工件台输出位移；e（a）为系统单轴跟踪误差。

为提高此系统动态响应特性，即保证在输入指令轨迹时变的过程中，系统能够快速、准确地实现对目标指令轨迹的跟踪，避免单轴跟踪误差受到自身系统和耦合系统的共同影响，基于单轴跟踪误差定义控制系统的目标函数如下：

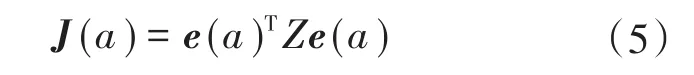
式中：Z为自定时非零正整数。

根据数值分析相关理论，式（5）的目标函数为凸函数，为确定其迭代更新率求解过程，首先确定初始前馈控制参数向量a0和正定矩阵Q，如下式所示：

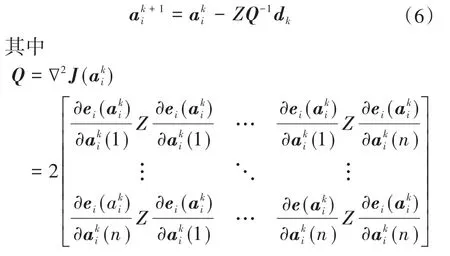
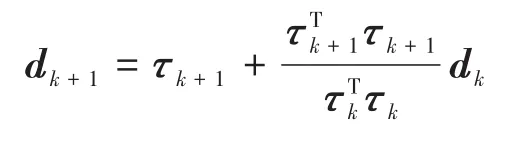
式中：dk为迭代运算中间变量；k，i分别为迭代次数和F（a）中的第i个元素；∇为梯度运算符号；τk为相互共轭且线性无关的向量，此向量可在初始化阶段设定，满足求解方程要求即可。在迭代计算过程中τk表达式如下式：

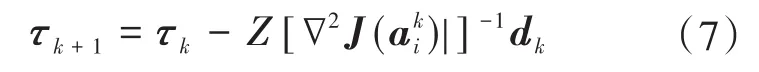
式（7）中，τk为方程求解初始化阶段设定的向量参数，在迭代计算过程中，需要根据τk的残差判断方程求解的停止条件，即τk为方程求解精度设定向量，在实际应用过程中，根据所需计算精度、处理器运算能力与计算效率匹配确定。

3 控制方法收敛性分析

针对第2节的前馈控制器参数向量确定方法，本节将对参数向量确定方法的收敛速度和收敛精度进行分析。根据式（5）所示的目标函数可知其满足凸函数定义，假设ao为目标函数的最优解，若目标函数二阶连续可导，则目标函数满足下式：

且若目标函数的最优解为ao，则对目标函数J（a）在最优解点进行泰勒函数展开，有：

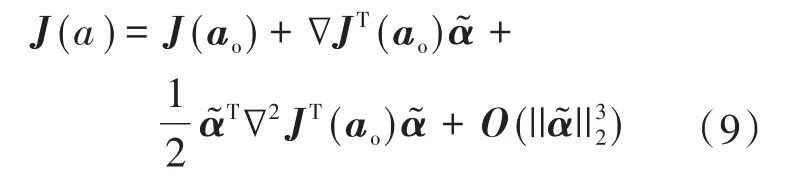
式中：为前馈控制器参数向量与最优解目标向量的残差值。

此时联立式（8）和式（9）可以得到：

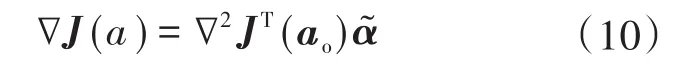
进一步可求得残差的表达式：

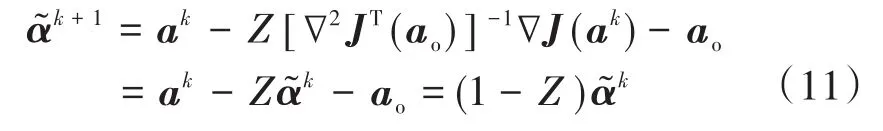
若保证前馈控制器参数向量不断收敛，则需要残差向量满足下式：

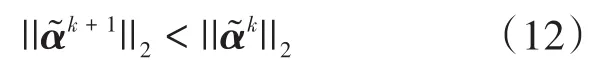
即对式（11）两边取范数后，需使不同迭代次数的残差向量满足式（12），将式（11）和式（12）联立可得：若前馈向量满足收敛特性，则需要Z满足条件0＜Z＜2。

若使前馈控制器参数向量收敛速度快，则根据式（12）可知：若Z=1时，理论上其可以实现快速收敛，通过1次迭代计算即可得到最优前馈控制器参数向量。但是，由于机电系统在数学建模过程中包含简化环节，如机械平台的死区非线性、迟滞滞回特性以及电机电感等非线性环节，在迭代计算过程中不可避免地产生系统误差，因此收敛特性会受到影响。在确定前馈控制器参数向量过程中，通过多次迭代优化可以降低上述非线性环节的影响，得到前馈控制器参数向量最优解。

上述前馈控制器参数向量确定方法和收敛性分析是针对单轴伺服展开的，对于图2所示的交叉耦合前馈控制器，前馈控制器结构和迭代优化方法相同，即通过优化前馈控制器结构和参数确定最优解，实现对单轴系统本身及其他自由度对本轴影响的有效补偿。

4 仿真试验验证

为验证所提迭代优化更新方法的正确性和收敛性，利用Matlab/Simulink对其算法验证。仿真试验中采用的控制器及被控对象参数为：工件台等效质量M=1.25 kg，工件滑动阻尼系数B=0.625 N/（m·s-1），控制器比例系数Kp=676.4，控制器积分系数Ki=10 146.1，控制器微分系数Kd=0。基于以上的被控对象和控制器参数，利用基于轨迹信息的前馈控制器实现迭代优化控制，判断迭代更新方法的收敛速度和收敛精度。

针对控制系统模型和控制器，以文献[14]中指令轨迹为参考位置输入进行仿真分析，利用所提的前馈控制器参数向量迭代优化方法进行参数的迭代更新，图3为10次迭代计算过程中迭代次数与目标函数的关系。由图3可见，本文所提方法能够在较短迭代过程中实现收敛，收敛速度较好，且随着迭代计算次数的增加，其目标函数能够收敛到全局最优。

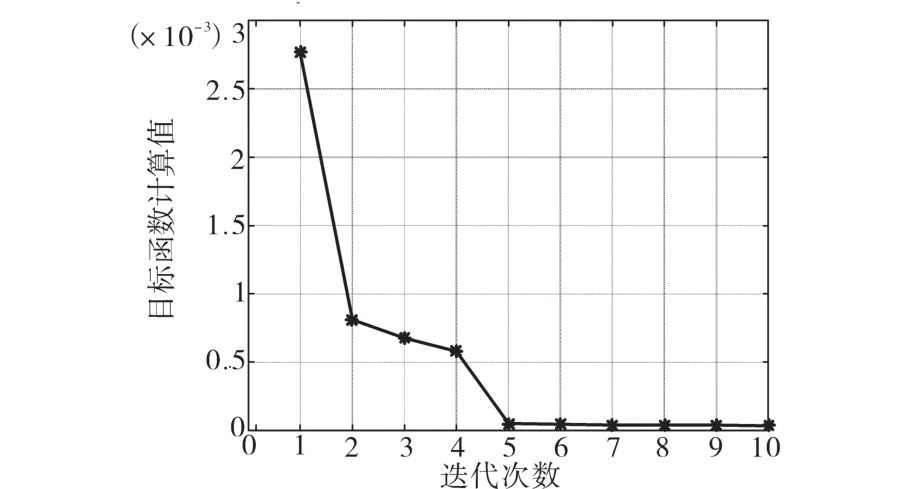
图3 迭代优化方法的收敛性分析Fig.3 Convergence analysis of iterative optimization method

图4为传统交叉耦合算法和本文所提出的基于迭代优化控制方法的比较。由图4可知，利用传统交叉耦合算法，其最大跟踪误差为0.7 μm，而利用迭代优化控制方法对交叉耦合控制器优化后，其最大跟踪误差在0.2 μm以内，据此通过仿真验证了所提算法的有效性。

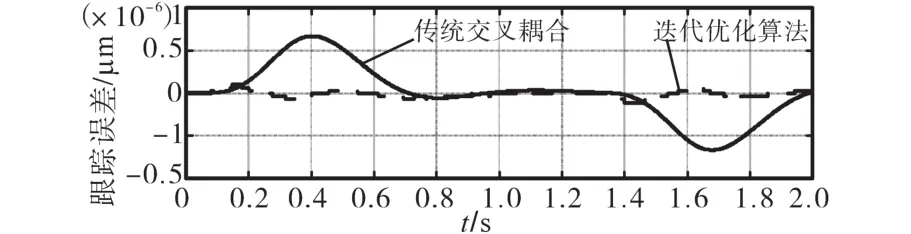
图4 传统交叉耦合与迭代优化算法比较Fig.4 Comparison of traditional cross-coupling and iterative optimization algorithms

为进一步验证所提方法的适用性和通用性，通过XY两自由度试验平台进行试验。两自由度试验平台机械部分由THK滚珠丝杠和联轴器组成，电气部分包括自研的控制板卡和台达旋转交流伺服电机等，利用道尔光栅作为位置反馈传感器，其分辨率为1 μm。基于上述试验平台，对匀速位置指令和正弦位置指令分别试验，利用本文所提的迭代前馈控制器参数优化方法，采集单轴跟踪误差来对比说明不同控制方法的动态性能。

图5为在10 mm/s的指令速度下，传统PID控制器和基于迭代优化控制方法所对应的单轴跟踪误差，基于传统PID控制器的单轴跟踪误差的均方根值为21.3 μm，利用迭代优化的PID控制器试验平台的单轴跟踪误差的均方根值为13.7 μm。

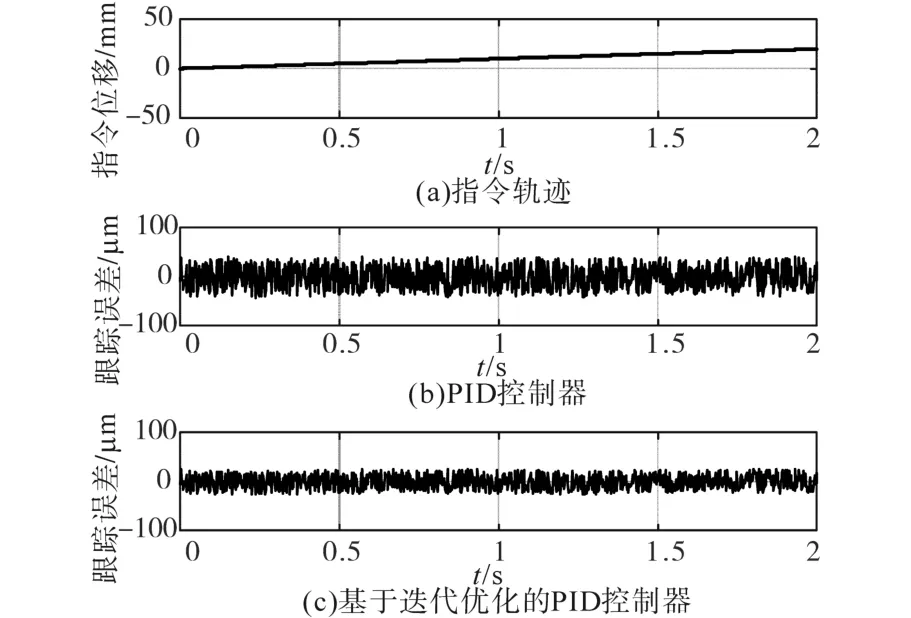
图5 匀速指令下单轴跟踪误差Fig.5 Uniaxial tracking error under uniform speed command

与此同时，在幅值为50 mm、周期为1 s的正弦位置指令输入下，基于PID控制器（初始状态）和迭代优化后的试验结果如图6所示，传统PID控制器所对应的单轴跟踪误差均方根值为88.3 μm，利用迭代优化前馈控制器的控制方法其单轴跟踪误差的均方根值为25.6 μm；由于驱动控制过程中采用d-q轴控制方法，根据图7的q轴电流采样可见，初始状态下其q轴采样值的最大值为350 mA，经过迭代优化计算后q轴采样值的最大值为200 mA，即通过迭代优化后的控制方法能够通过前馈交叉耦合前馈控制适量补偿，从而减少控制器作用，提高系统动态跟踪精度。

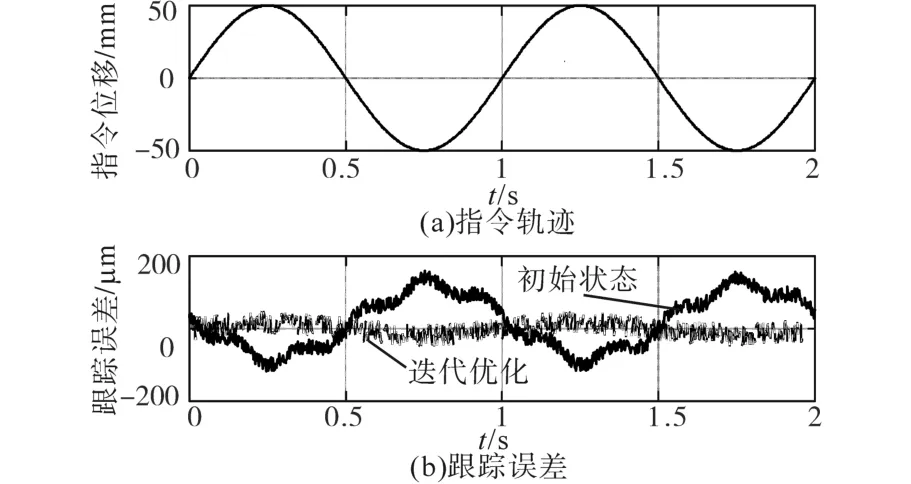
图6 正弦指令下单轴跟踪误差Fig.6 Uniaxial tracking error under sinusoidal command

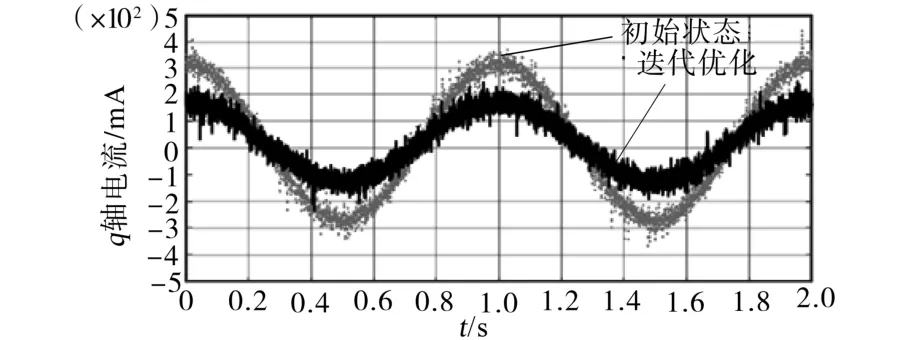
图7 正弦指令下q轴电流采样Fig.7 Sampling of q-axis current under sinusoidal command

综上所述，基于迭代优化的多电机交叉耦合控制方法能够有效提升机电系统的动态控制精度，根据匀速位置指令和正弦位置指令的试验结果可以发现，基于轨迹的前馈控制器结构及其参数优化方法能够有效提升系统动态特性，且优化方法具有较好的收敛速度和收敛精度，为实际工程应用奠定基础，为解决多轴电机同步控制及交叉耦合问题提供思路。

5 结论

为提高多电机同步控制性能及多自由度机电系统的动态特性，本文提出一种基于迭代优化的多电机交叉耦合控制方法。首先，针对机电系统进行数学建模，利用经典控制器理论推导系统传递函数；其次，设计合理的前馈控制器结构并提出有效的前馈控制器参数优化方法；再次，对所提方法进行了收敛速度和收敛精度的分析；最后，通过仿真和试验验证了所提方法的正确性和实用性。本文所提控制方法能够通过离线迭代优化，实现目标函数的快速收敛，有效降低了控制器在线运算负载和算法实现难度。