基于离散概率分布的分布式光伏电站优化配置

刘海涛，许伦，郝思鹏，张潮，孙晓

（1.南京工程学院电力工程学院，江苏南京211167；2.江苏省配电网智能技术与装备协同创新中心，江苏南京211167）

随着我国分布式光伏的快速发展，一些地区已经形成了高渗透率分布式光伏并网的典型区域[1]，如浙江嘉兴光伏产业园、江苏宝应渔光互补产业基地、宁夏中卫光伏产业园等。其中，浙江嘉兴光伏产业园的光伏全年能量渗透率更是高达40%～50%，但由于配电网的消纳能力不足，较高的光伏渗透率已经对电网的安全稳定运行和系统的运营成本造成了不利影响，也出现了严重的弃光现象。已有研究表明[2-5]，在电源规划阶段考虑光伏电站出力的波动性是在现有技术下有效缓解大规模、高渗透率分布式光伏电站接入配电网不利影响的有效方法之一。

目前，针对分布式光伏电站的规划问题，文献[2]采用多场景分析法和K-mean均值聚类方法模拟全年光伏电站波动性对配电网影响的典型场景，考虑各个场景光伏电站的出力和概率进行规划。文献[3]建立随机规划模型模拟新能源系统的运行，并且采用Benders分解算法对新能源出力的情况进行求解。针对波动性分布式电源的离散化，文献[4-5]基于分布式电源出力的一般性特征，采用累积分布函数计算各个离散点的概率，基于离散点的概率以全概率计算公式计算各个分布式电源组合后场景出现的概率，文献[6]以beta分布函数计算光伏功率的累积分布情况，采用拉丁超立方采样模拟各个离散点功率情况。

上述研究提供了很多开创性思路，但同时也存在着一些问题。

1）在电源规划方面，已有文献中多是采用典型场景的生成和缩减，将具有波动性的光伏电站转变为具有稳定出力恒功率电源，其计算复杂度较高，模型精度受历史数据的影响。在离散化处理方面，已有文献又大多脱离分布式电源的典型场景，采用分布式电源一般性特征进行计算，忽略各个电源的独有“特性”。

2）随着大量实际工程数据的反馈，已有文献仅仅通过设置2～3个目标对模型进行规划难以达到最优配置，应该从多个角度考虑，但是目标函数设置的过多会造成求解模型出现“维数灾难”，如何解决多目标的实际需求和降低求解难度的矛盾也亟待解决。

基于以上分析，本文在分布式光伏电站的规划中，采用计算复杂度低的离散概率分布表征光伏电站出力的概率特征，将光伏出力离散化为固定场景下的稳定出力，建立双阶段配置优化模型，第1阶段考虑主要目标对分布式光伏电站的接入位置和容量进行优化，第2阶段考虑次要目标对第1阶段的配置方案进行评价，并且应用具有高收敛性的蚁狮算法对所建立的非线性模型进行求解。

1 光伏电站输出功率离散化

分布式光伏电站安装地点的光照强度、气候特征以及季节因素可以通过光伏电站的典型日功率输出曲线有所表现，本文采用离散概率分布表征光伏电站典型日功率输出曲线的概率特征，假定光伏电站输出功率在0和额定容量Pe之间波动，根据光伏电站功率的输出波动情况和配电网的规模，设置离散区间个数h，则输出离散化功率步长为Pstep=Pe/h，那么离散区间内的功率输出值计算公式为

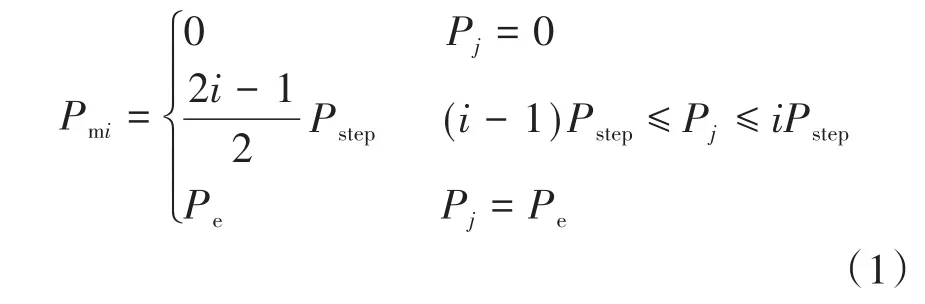
式中：Pmi为离散区间i的区间输出值；Pj为第j个采集点的有功输出值。

显然，离散区间个数h的选择对本文优化过程的复杂度及优化结果的精度具有明显影响，离散区间数目设置过少，离散化结果与实际曲线相差过大，不能很好反映光伏电站出力的概率分布特征，精度下降；离散区间设置过多可以提高运算精度，但会显著增加本文配置算法的计算复杂度。

根据已有文献分析，随着离散区间数目的增大，离散化结果与实际输出曲线的差值变化趋势逐渐减缓，存在一个最合适的区间数目[7]，故本文为量化离散化结果与实际输出曲线的误差，建立能量差指标和能量差变化指标，如下式：

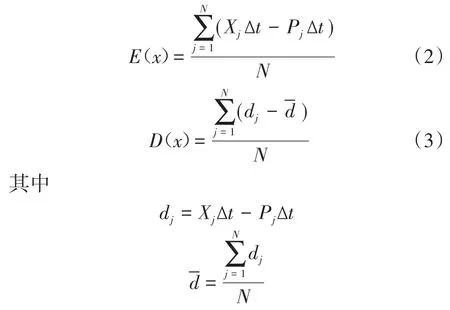
式中：E（x）为离散化结果与实际输出曲线的能量差；N为输出曲线采样节点数；XjΔt为Δt时间内离散化后的光伏输出的能量；PjΔt为Δt时间内光伏实际输出的能量；D（x）为离散化结果与实际输出曲线的能量差变化。

统计光伏电站各个采集点有功出力样本落在各个离散区间的频数，计算相应的概率如下：

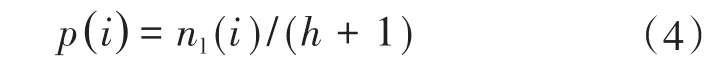
式中：p(i)为区间i出现的概率；n（li）为离散区间出现的次数。

2 优化配置模型

本文建立考虑主要因素和次要因素的双阶段配置优化模型，第1阶段以电站投资成本和系统网损为主要目标对分布式光伏电站的接入位置和容量进行优化，第2阶段以系统电压偏差、系统稳定程度和电站弃光率为次要目标，应用模糊贴近度对第1阶段的配置方案进行评价，并且目标函数的计算考虑光伏电站的离散概率分布。

2.1 主要因素

1）电站投资成本如下式：

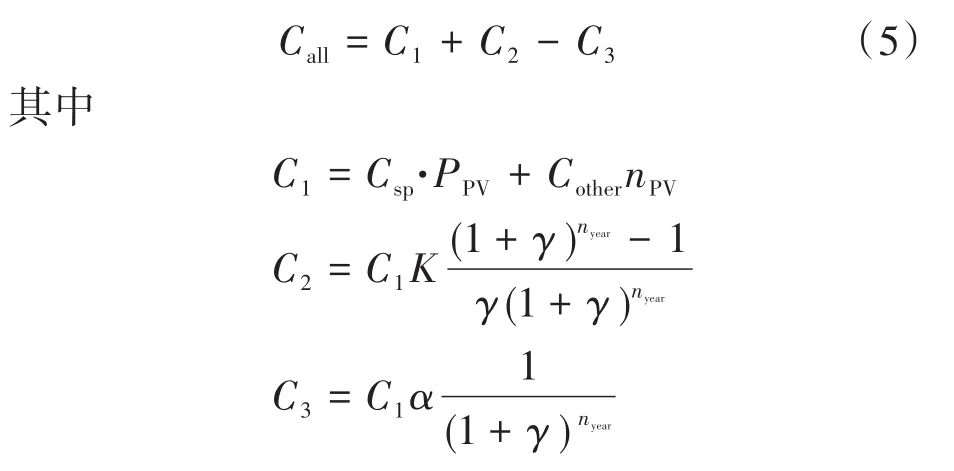
式中：Call为电站投资成本；C1为初始投资成本；C2为设备运行成本；C3为报废时设备残值；Csp为太阳能电池板单位价格；PPV为光伏电站容量；Cother为光伏电站配套投资；nPV为待建设光伏电站数目；K2为C1按照C计算的比例系数；[(1+γ)nyear-1]/[γ(1+γ)nyear]为等年值求现比率；γ为折现率；nyear为工程运作总周期；α为设备报废时残值占初始投资成本的比率；1/[(1+γ)nyear]为将来值求现比率。

2）系统网络损耗如下式：

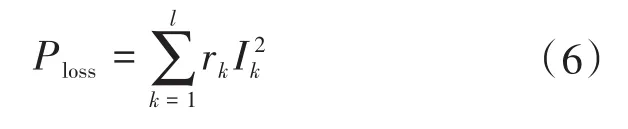
式中：Ploss为配电系统的网络损耗；l为系统支路数；rk为系统k支路电阻；Ik为系统k支路通过的电流。

考虑光伏电站离散概率分布后的主要因素计算模型如下：

①电站投资成本：

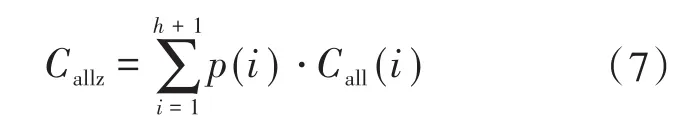
式中：Callz为加权计算后的电站投资成本；p(i)离散区间i出现的概率；Call(i)为在离散区间i条件下的电站投资成本。

②系统网络损耗：

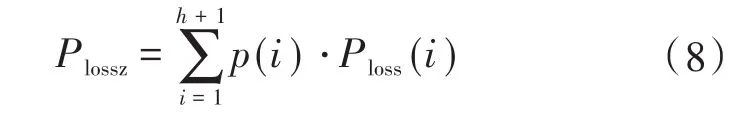
式中：Plossz为加权计算后的系统网络损耗；Ploss(i)为在离散区间i条件下的系统网络损耗。

2.2 次要因素

1）系统电压偏移如下式：

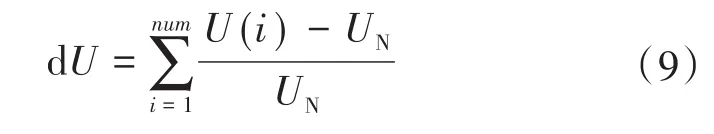
式中：dU为系统电压偏移累和；U(i)为第i个节点电压值；UN为系统额定电压；num为系统节点数目。

2）系统稳定指标。文献[8]提供了计及分布式电源接入的配电网电压稳定性评估指标VSI，定义节点j的VSI为

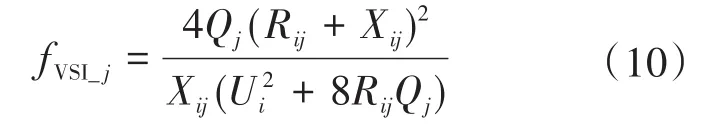
式中：fVSI_j为节点j的 VSI值；Qj为节点j送出的无功功率；Rij+Xij为线路ij的阻抗。

本文以所有节点VSI的最大值max（fVSI）作为评价配电网的系统稳定性的指标。

3）电站弃光率如下式：

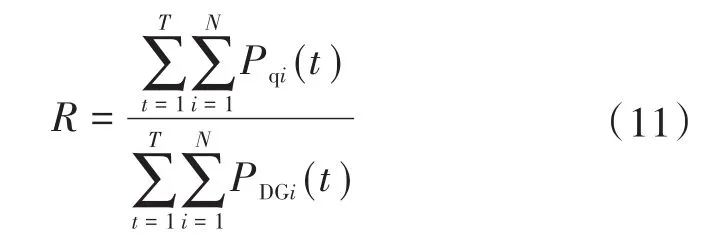
式中：R为弃光率；T为统计时间尺度；N为接入配电网的分布式光伏电站的个数；Pq（it）为t时刻分布式光伏电站i的弃光功率；PDG（it）为t时刻分布式光伏电站i的发电功率。

考虑光伏电站离散概率分布后的次要因素计算模型如下：

①系统电压偏移：

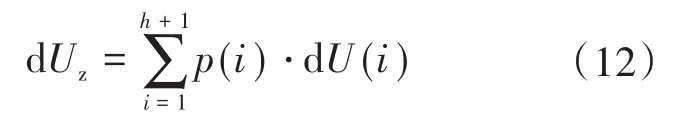
式中：dUz为加权计算后的系统电压偏移；dU（i）为在离散区间i条件下的系统电压偏移指标。

②系统稳定指标：

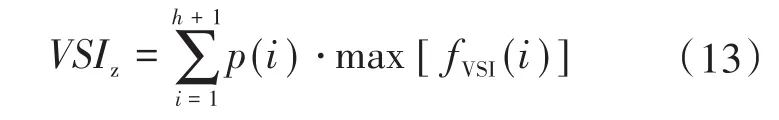
式中：VSIz为加权计算后的系统稳定指标；max[fVSI(i)]为在离散区间i条件下的系统稳定指标。

③电站弃光率：

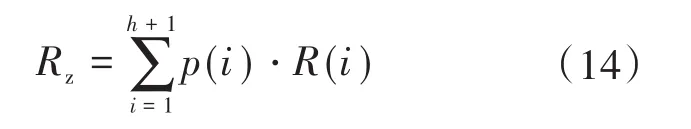
式中：Rz为加权计算后的电站弃光率；R（i）为在离散区间i条件下的电站弃光率指标。

2.3 约束条件

1）功率平衡约束如下式：

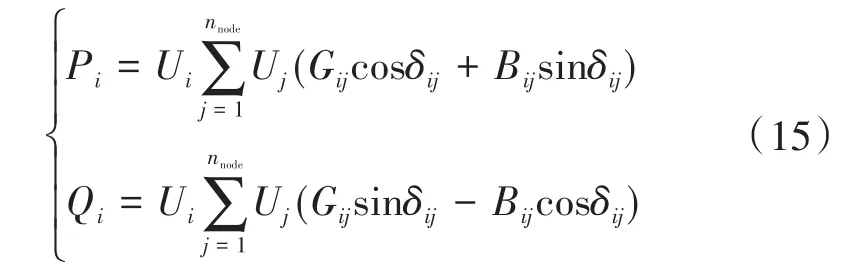
式中：Pi，Qi分别为节点i向系统注入的有功功率、无功功率；nnode为系统的节点数；Ui，Uj分别为节点i，j电压向量的幅值；Gij为节点导纳矩阵元素Yij的实部；Bij为节点导纳矩阵元素Yij的虚部；

2）电压约束如下式：

式中：Umin，Umax为节点电压允许的上、下限，一般电压正、负偏差的绝对值之和不超过额定值10%。

3）容量约束。本文根据现实发展情况，以配电网电压稳定性评估指标VSI约束代替传统的分布式电源容量约束，约束条件如下式：

3 蚁狮算法

多目标蚁狮算法（multi-objective ant lion optimization，MALO）设置Ant和Antlion两个种群，通过Antlion设置陷阱的位置和大小确定算法的搜索范围，通过Ant被陷阱吸引，围绕Antlion随机游走实现对搜索空间的探索，通过Antlion捕食Ant实现解的更新[9-10]。

利用MALO解决待优化问题主要有4个环节：

1）Ant随机移动，其步骤如下：

①Ant中所有个体按下式开始随机移动：

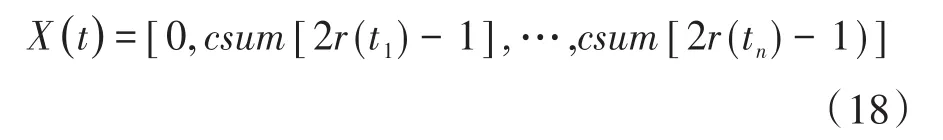
式中：csum为累积和；ti为当前迭代次数；（rt）产生随机数0或1。

②Ant中个体按下式修正移动过程，防止个体越界：

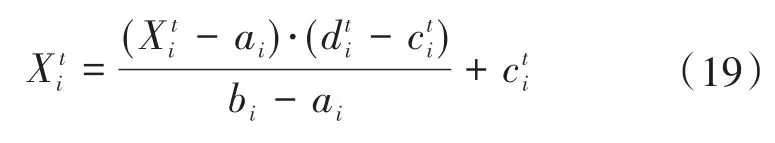
2）Ant陷入陷阱，其步骤如下：

①Ant中个体移动边界受Antlion位置的影响，按下式向陷阱偏移：

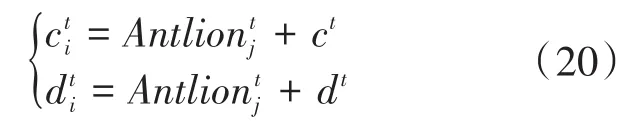
②Ant中个体进入陷阱且逐步滑落到陷阱底部，其过程可以视为Ant中个体按下式逐渐缩小其移动范围：

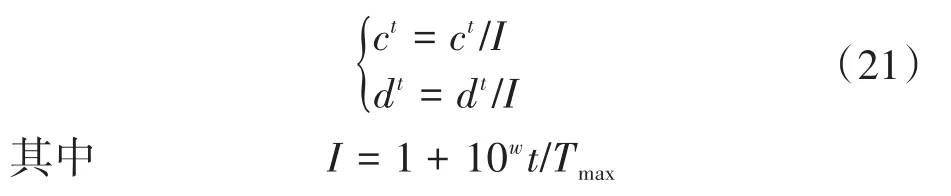
式中：I为移动范围缩小的速率；t为当前迭代次数；Tmax为最大迭代次数；w受当前迭代次数的影响。

3）Antlion捕食Ant，其过程的数学表示式为

4）精英化Ant，其过程的数学表示式为

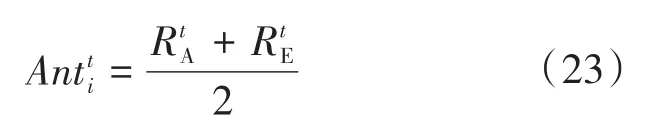
算法流程如图1所示。

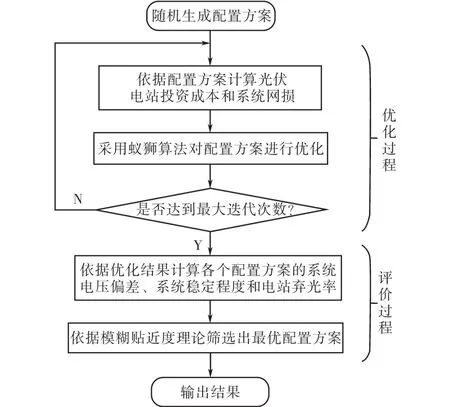
图1 算法流程图Fig.1 Algorithm flowchart

4 算例分析

算例分析中，研究重点在于考虑光伏出力波动性对配电网的影响，采用离散概率分布表征光伏电站典型日功率输出曲线的概率特征，故而光伏出力场景采用工程中实际电站提供的典型日数据进行分析，IEEE-33节点配电系统如图2所示。以IEEE-33节点配电系统为研究对象，分布式电源均视为PQ节点，其功率因数为0.9。

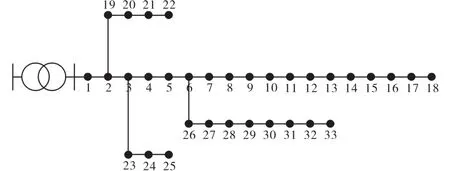
图2 IEEE-33节点配电系统Fig.2 Distribution system of IEEE-33 node

4.1 参数设置

分布式电源在规划时，太阳能电池板单位价格为0.3万元/kW，配套投资成本为1.5万元/套，折现率为6.7%，工程年限为20 a，维护比例K为10%，残值比例α为5%。

算法设置中，Ant种群和Antlion种群大小均为100，存储档案大小为100，最大迭代次数为100，2-33节点为备选安装节点。

4.2 结果分析

1）分布式光伏离散化结果。

本文通过能量差指标和能量差变化指标对离散区间数目设置情况进行分析，结果如图3所示。数目超过6以后，误差改善情况提高并不明显，并且出现反复，故设置离散区间数h为6个，离散化结果如图4所示。

图3 离散化误差分析Fig.3 Discretization error analysis

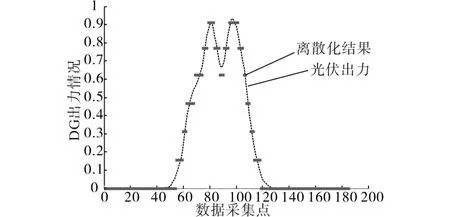
图4 离散化结果Fig.4 Discretization result

2）多目标优化结果及分析。

根据主要目标优化模型，按照MALO算法进行求解并与应用最为广泛的NSGA-II求解结果进行对比，结果如图5、图6所示。

图5 算法收敛情况对比Fig.5 Comparison of algorithm convergence

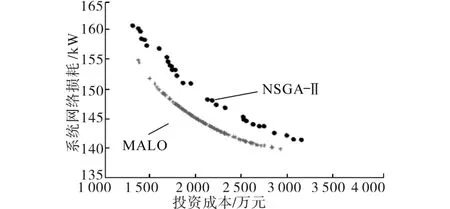
图6 算法求解结果对比Fig.6 Comparison of algorithm results

由非劣解分布情况可以看出，MALO算法具有更高的精度、更快的收敛速度。

考虑系统电压偏差、系统稳定程度和电站弃光率等因素，采用模糊贴近度对非劣解集进行评价，选择第33套方案为最优配置方案，并与其附近方案进行对比，结果如表1、表2所示。

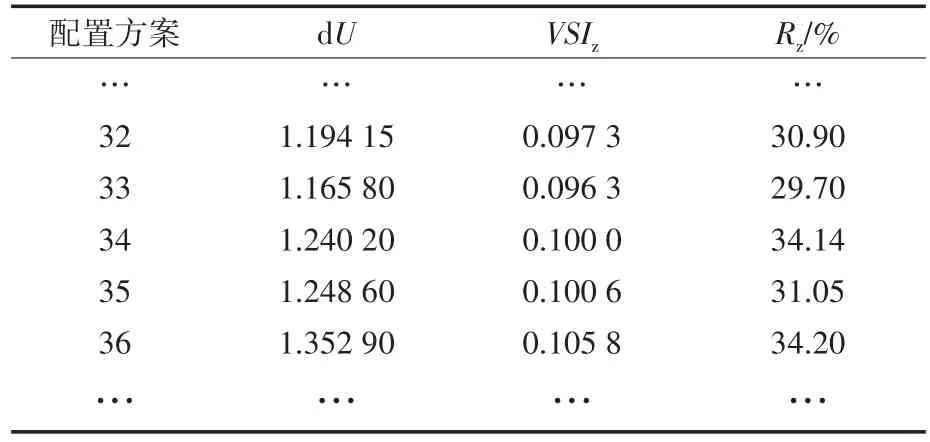
表1 N0.32～N0.36配置方案评价指标Tab.1 N0.32～N0.36 configuration plan evaluation index

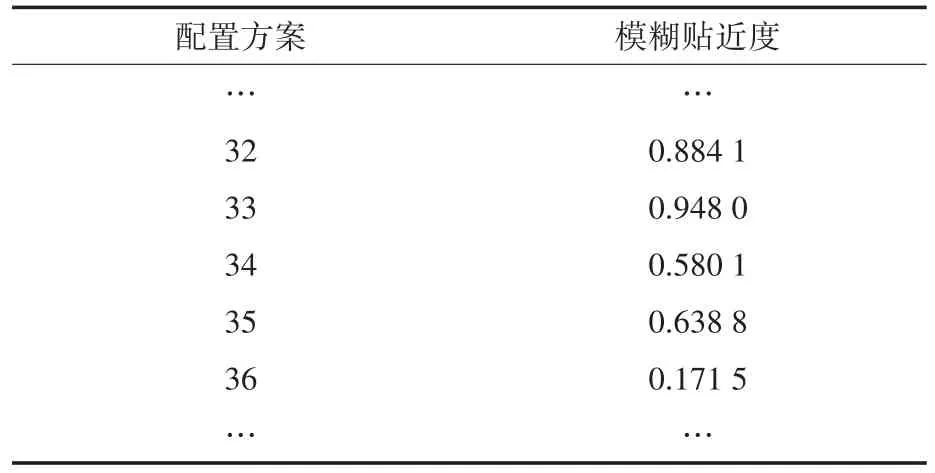
表2 N0.32～N0.36配置方案模糊贴近度Tab.2 N0.32～N0.36 configuration scheme fuzzy closeness

本文提出的方案与忽略光伏电站出力的波动性的配置结果进行对比[11-12]，两者最优配置方案如表3，其相关指标结果如表4所示。

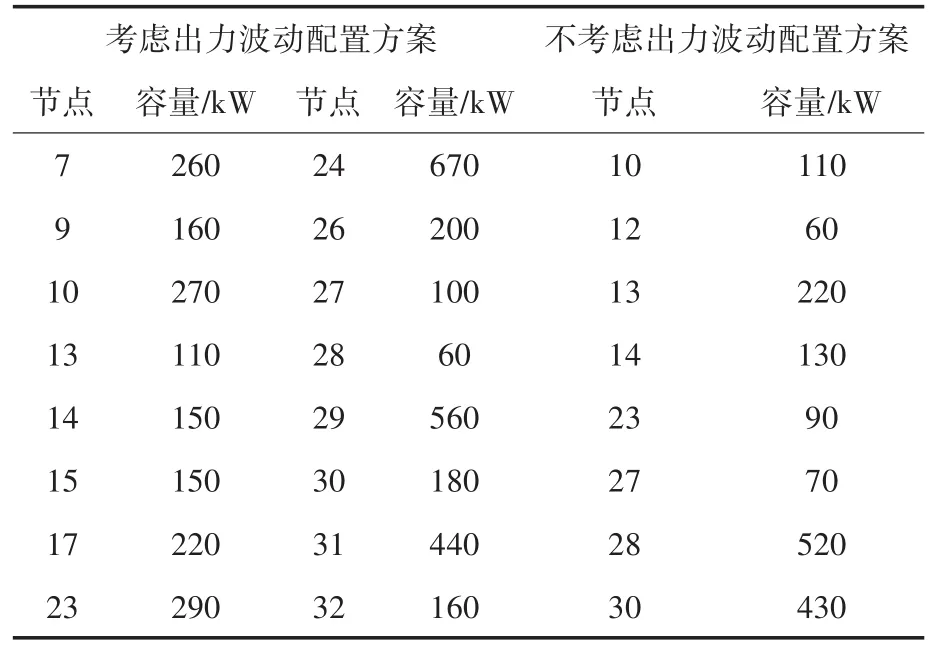
表3 分布式光伏电站配置方案Tab.3 Distributed photovoltaic power plant configuration

表4 指标数据Tab.4 Indicator data

5 结论

本文为解决较高的光伏渗透率情况下分布式光伏电站的规划问题，充分考虑光伏出力波动性对配电网的影响，采用离散概率分布表征光伏电站典型日功率输出曲线的概率特征，并且从电站投资成本、系统网络损耗、电压偏移量、系统的稳定程度以及电站弃光率5个角度构建离散化后的双阶段配置优化模型，第1阶段以电站投资成本和系统网损为主要目标对分布式光伏电站的接入位置和容量进行优化，第2阶段以系统电压偏差、系统稳定程度和电站弃光率为次要目标，应用模糊贴近度对第1阶段的配置方案进行评价。

结果表明，在光伏电站规划阶段考虑其出力的波动性虽然造成投资成本的上升，但可以更有效地提高分布式电源对配电网的支撑作用，在系统网络损耗、电压偏移量、系统的稳定程度方面有明显的改善，并且与不考虑出力波动配置方案相比，虽然配置容量增大，但是弃光率明显下降，表明了本方案的合理性，对分布式光伏电源的利用率明显提高。