考虑输出功率相关性的光伏电站典型场景生成方法研究

陈颢元，蒋玮，韩俊

(1.东南大学电气工程学院,江苏 南京 210096；2.国网江苏省电力有限公司经济技术研究院，江苏 南京 210008)

0 引言

当前，分布式光伏发电在配电网中的渗透率逐年提升[1—7]。由于光伏发电系统输出功率本身具有极强的随机性和波动性，有效评估配网系统电压风险的需求变得日益迫切。概率潮流计算是一种评估配网系统电压风险的重要手段[8—11]。在使用模拟法进行概率潮流计算时，其准确性很大程度上取决于输入变量建模的准确性[12—15]。因此，在光伏接入评估等计算应用时，应综合考虑各因素对光伏电站输出功率的影响，生成典型性的场景模型作为蒙特卡洛方法的抽样对象[16—18]。

目前，配电系统的光伏输出功率建模仍不完善，这是由于传统使用的Beta、Weibull等概率模型往往不能真实地反映实际运行状态[19—20]。在光伏高渗透率配电系统中，一个集中区域内往往存在多个光伏电站，其参数、地理位置和运行时间之间均存在相关性。为考虑电站之间的相关性，文献[21—22]在光伏电站建模中分别引入了NATAF变换和Cholesky分解。文献[23]使用Copula函数直接获取各光伏电站输出功率的联合概率分布。文献[24]提出混合Copula函数建模法，使用欧式距离判定最优Copula函数。该文献指出：受气象、光照、运行方式等外界条件影响，各光伏输出功率之间的相关性可能会发生变化，单一的概率模型不能很好地应对外界条件的变化。文献[25]提出利用K-means聚类和Copula函数来建立多场景概率模型，其中K-means聚类的参数确定常依赖经验。

针对上述问题，文中引入了一种基于局部密度中心的聚类算法(local density clustering,LDC)。首先，提出考虑相关性的光伏输出功率多场景模型建立方法。该方法结合LDC聚类方法、核密度估计法和Copula函数，将各光伏输出功率联合分布函数场景化。其次，对生成的多场景概率分布模型进行抽样，对生成的样本进行概率潮流计算。模型考虑多个光伏电站输出功率间相关性以及输出功率随外界条件的变化，可实现配电网多个光伏输出功率的精准建模。最后，为验证文中方法的可靠性，将场景优化方法应用于某地区实际配电网结构的节点系统，进行算法性能分析。

1 考虑相关性的多光伏电站概率分布建模

1.1 单个光伏电站的概率分布估计

为计算概率潮流，须获得配电网光伏输出功率以及负荷的概率分布。在估计未知随机变量的概率密度函数时，须对已知概率密度函数的参数形式进行估计。由于Beta分布、Weibull分布等一些常见的概率密度形式往往不能准确反映实际概率分布，故文中采用核密度的方式进行估计。

核密度估计法要求使用平滑的峰值函数(即核函数)来拟合数据样本。对于满足独立同分布的n个样本点(x1,x2,…,xn),设其概率密度函数为f，则核密度估计函数为：

(1)

式中:K(·)为核函数;h为平滑参数，称作带宽;Kh(x)为缩放核函数，如式(2)所示。

(2)

核函数的选择需要符合概率密度性质,常用的核函数包括方波函数、三角函数、双峰曲线、三峰曲线、高斯曲线等。文中选用高斯核函数，即K(x)为高斯分布的概率密度函数，如式(3)所示。

(3)

作为一种非参数化方法，核密度估计法面对任意的概率分布无须预先假设已知的标准形式。由于该方法具有较好的预期准确度，因此可被用于估计光伏输出功率和负荷的概率分布情况。

1.2 多个光伏电站的概率分布估计

文中采用核密度估计法得出配电网中的各光伏输出功率，推导出若干单个光伏输出功率的概率模型。当配电网接入多个光伏电站时，场景生成建模应考虑模型间的相关性。因此，文中采用Copula函数理论获取多个光伏电站的联合概率分布。

Copula函数能将多维随机变量的联合分布函数与各自的边缘分布函数连接起来，为求取联合分布函数提供灵活的方法。

对于边缘分布函数F1(x1),F2(x2),…,Fn(xn)，存在一个Copula函数C满足：

F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]

(4)

当F1(x1),F2(x2),…,Fn(xn)连续时，Copula函数C唯一确定。文中将服从任意分布的xi转换为均匀分布ui=Fi(xi)。

常用的Copula函数主要有高斯Copula 函数、t-Copula函数、Gumbel Copula函数、Clayton Copula函数和Frank Copula函数等。不同的Copula函数在描述随机变量相关性方面具有明显的差异[26]。Copula函数的构造步骤为：首先，确定各随机变量的边缘分布；然后，选取合适的Copula函数形式；最后，估计模型中的参数。

针对以上步骤，文中采用核密度估计的结果作为随机变量的边缘分布，选取欧式距离法确定最优的Copula形式以描述输出功率的相关结构，并使用极大似然方法对模型进行参数估计。文中构建的基于Copula函数的概率模型可准确描述配电网多个光伏电站输出功率的概率特性，并反映光伏输出功率等随机变量之间的相关性。

2 基于局部密度中心的光伏电站历史数据聚类

基于Copula函数的光伏电站建模方法考虑了多个输出功率之间的相关性，但未考虑到相关性可能随天气、运行方式等外界因素影响发生的变化。因此，本节借助聚类这一数据挖掘方法，将单一的概率函数模型改进为多场景模型。文中使用核密度估计和Copula函数，对每个场景下的数据分别估计输出功率的联合概率分布，进行精细化建模。

聚类分析可挖掘数据样本之间的内在规律，该方法已广泛应用于电力系统的场景生成、故障筛选等领域。由于常见的K-means聚类方法存在对噪音和异常点敏感、依靠经验确定类数等问题，文中使用LDC聚类算法来确定聚类中心，定义样本的局部密度作为聚类依据。该方法可自动生成类数和聚类中心[27]，并剔除异常点。光伏输出功率LDC聚类流程如图1所示。

图1 光伏输出功率LDC聚类流程Fig.1 Diagramfor LDC clustering of PVoutputs

LDC聚类算法的具体步骤如下：

(1) 假设配电网接入的光伏电站数量为N，获取N个电站输出功率的历史数据构成原始数据集P。Pi=(Pi1,Pi2,…，PiN)为数据集P内的其中一个样本点，表示某一时刻i下所有光伏电站的输出功率，是一个N维向量。

(2) 对每个输出功率样本点Pi，定义每个样本点的局部密度函数ρi为：

(5)

式中:dc为截断距离，是预先设定的参数；dij为2个样本点之间的距离。对于函数χ(a)，当a>0时，其值为0，否则为1，如式(5)所示:

(6)

(3) 定义每个样本点的距离偏量δi，其含义为所有局部密度大于样本点Pi的样本点到Pi的距离的最小值，即：

(7)

(4) 确定聚类中心。聚类中心需要满足以下条件：样本点本身的局部密度ρi大于周围点的密度，且样本的距离偏量δi应尽可能大。综合考虑以上条件，建立指标ρi×δi。当该指标大于设定的阈值，判定该点为一个聚类中心。

(5) 对其余样本点归类。首先，对样本点按ρi降序排列；其次，选取Pi，Pj，根据Pi的具体情况选取Pj，Pj满足局部密度高于ρi且距离值dij最小，把Pj的类别标号赋给Pi；最后，根据局部密度的降序依次对样本点进行类别赋值，形成多个场景。

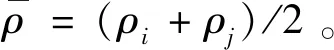
3 基于多场景模型的概率潮流计算

3.1 场景生成流程

文中建立一个多光伏电站输出功率模型，该模型将各光伏电站输出功率的相关性及相关性随外界条件的变化考虑在内。在对数据进行LDC聚类后，通过核密度估计法和Copula函数获取各光伏电站输出功率联合分布函数，并将其场景化。基于多场景模型的概率潮流计算流程如图2所示。

图2 基于多场景模型的概率潮流计算流程Fig.2 Probabilistic power flow calculation based on multi-scenarios model

场景生成的具体步骤如下：

(1) 获取配电网络下所有光伏电站的历史数据，并进行数据清洗和预处理。

(2) 对数据集进行LDC聚类，产生N类场景，按照各场景建模，形成光伏输出功率多场景模型。

(3) 使用核密度估计方法，按场景获取各光伏电站的边缘概率密度函数。

(4) 对每类场景的边缘概率密度函数，构建各理论Copula函数，参数估计使用极大似然估计法。采用欧式距离法得到最优Copula函数，以此建模。

(5) 生成光伏输出功率样本。首先，使用拉丁超立方抽样(latin hypercube sampling,LHS)采样法[28—29]对每个场景下的Copula函数抽样。假设总采样数量为K，则每一场景下的采样数量Ki根据各场景发生概率进行确定。其次，对每一类中抽取的样本进行组合，生成全体光伏输出功率样本。

在进行配电网潮流计算时，除了光伏建模，还需考虑各负荷的概率分布。因此，使用核密度估计法进行估计时，先使用LHS采样法对概率分布进行采样，生成典型负荷样本。根据光伏输出功率和负荷样本的典型场景，结合蒙特卡洛法实现各场景的概率潮流计算，进而评估配电网的运行状态。

3.2 评价指标

(8)

(9)

式中：μa,i,σa,i分别为基准方法的节点电压均值和标准差；μc,i,σc,i分别为计算结果的节点电压均值和标准差。

(10)

式中：k为运行次数。

4 场景生成算例分析

4.1 算例结构

文中采用的算例基于某地区某实际配电网结构，相关配电网参数来源于该实际电网。系统的接线如图3所示。其中，2台光伏电站(PV1、PV2) 位于图1节点系统中的12、18号节点。

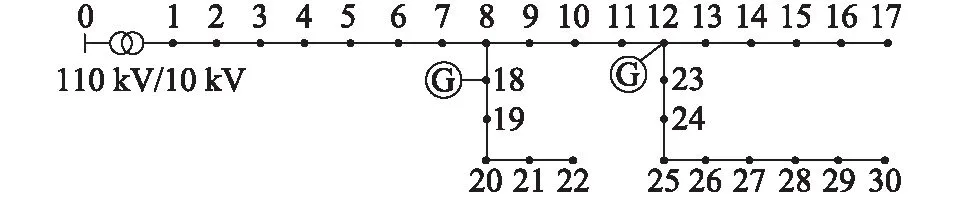
图3 配电网系统接线Fig.3 Distribution test system

所有节点的基准功率为100 MV·A，除0号变电站高压侧节点的基准电压为110 kV，其余节点系统的基准电压为10 kV。发电机组的额定容量均为1 MV·A，发电机组实际输出功率和各节点负荷的历史数据来源于实际的用电信息采集系统。

4.2 场景生成

对于PV1、PV2的输出功率历史数据进行LDC聚类，结果如图4所示。

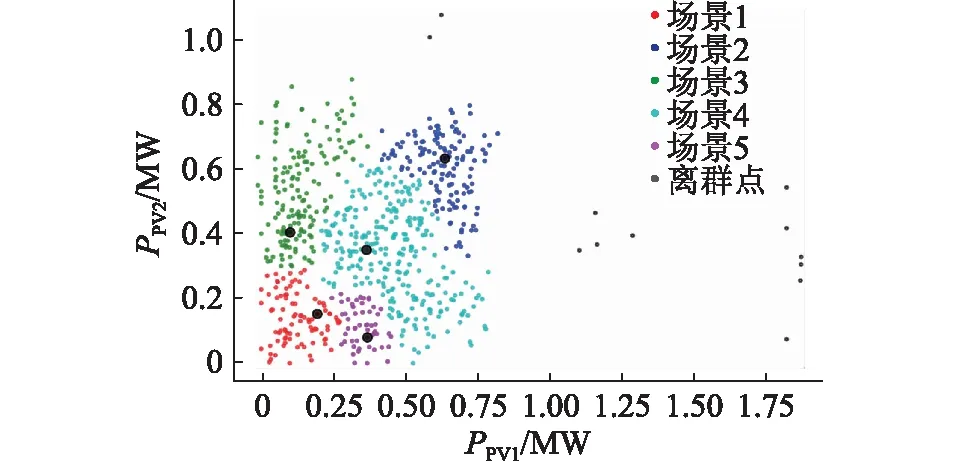
图4 光伏输出功率聚类结果Fig.4 Clustering Results for PV Output

由图4的聚类结果可知，光伏输出功率场景被分为5类，对应5个场景，黑色为离群点。每个场景下，2个光伏电站所有时刻有功输出功率构成的向量分别为：Pk1,Pk2(k=1,2,3,4,5)。为了对比各个场景下数据的相关性变化，统计5个场景和原始样本Pk1,Pk2之间的皮尔逊相关性系数ρPk1,Pk2。

(11)

式中：Cov(·)为协方差函数；σ(·)为标准差函数。

各场景的相关系数与原始样本差异见表1。

表1 皮尔逊系数相关性分析Table 1 Pearson coefficient analysis

由表1可知，单一的建模方法往往只能反映部分样本的相关性，无法适应所有样本。基于LDC聚类的光伏输出功率多场景生成方法有望解决这一问题。对各场景的输出功率进行核密度估计，如图5所示。

图5为各光伏电站在各场景下的边缘概率分布，其中坐标轴下方的黑线表示光伏输出功率在各场景下的样本，蓝色阴影表示通过核密度估计得到的边缘概率分布。根据各输出功率的边缘概率分布，按场景进行Copula 函数建模。使用欧式距离法得到该场景下的最优Copula函数，并统计各场景样本占比，生成结果如表2所示。同时对各Copula进行LHS采样，可得到概率潮流计算所需的样本。

图5 各场景下输出功率边缘分布Fig.5 PVs′ marginal distribution in different scenarios

表2 各场景Copula模型Table 2 Copula models of each scenario

4.3 潮流计算

表3 计算误差指标对比Table 3 Computing error comparision %

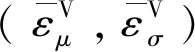
表4 算法稳定性分析Table 4 Method′s stability index

根据计算得到的节点电压概率分布，可以计算节点电压的期望值和置信区间，从而评估电压质量。根据国网经研院相关标准，电压允许偏差为正负7%，据此可计算出各节点电压的合格率和越限概率。

节点18在各场景下电压幅值统计情况如表5所示。各场景下的电压越限概率差距较大，其中电源输出功率最大的场景5达到了19.38%。运行与规划人员可根据各场景下电压越限概率，采取相应的措施以保障系统安全经济运行。

表5 节点18各场景电压幅值分析Table 5 Voltage magnitude analysis of node 18 in each scenario

4.4 采样规模对算法的影响

图6 采样规模对计算结果的影响Fig.6 Performance of different sampling number

由图6可知，对于LDC聚类方法、K-means聚类方法以及传统蒙特卡洛方法来说，取样次数N越大，算法误差越小。这3种方法均存在一个阈值，在采样数量方面提升至阈值后，计算精度的提升十分有限。由图6可知，文中方法的阈值小于基于K-means方法和蒙特卡洛法的阈值，且达到阈值所需的采样规模最低。这意味着，为了达到较为满意的精度，使用文中方法可采用更小的采样规模，从而减小算法的计算负担。在实际计算中，当误差达到阈值后，可停止增加采样数量。

5 结语

文中提出了基于LDC聚类的多场景生成方法，用于计算含有光伏接入配电网的概率潮流，从而进行配电网状态评估。该方法考虑了光伏输出功率相关性随电站运行方式等不同场景发生变化的情况，实现了更为精确的输出功率建模。相比于K-means聚类的建模方法，文中方法在计算精度和算法稳定性方面均实现了提升。

文中在建立配电网模型时，作出了配电网拓扑不发生改变的假设。而在中长期配电网的规划下,配电网拓扑将发生改变。因此，后续可以针对这一情况作出进一步研究。

本文得到国网江苏省电力有限公司科技项目“考虑光伏接入的配电网电压风险分析及最优接入容量规划技术研究”(J2019057)资助，谨此致谢！