玩中学演中悟 从三个水平层次管窥直观想象素养——以2020年浙江高考立体几何解答题为例

王峥嵘 王奇佳 沈 恒

(浙江省湖州市第二中学 313000)

《普通高中数学课程标准(2017 年版)》指出：数学学科直观想象素养主要表现在建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物.可以说，直观想象素养是数形结合思想的一种具体落实，在学生头脑中建立起从一维数轴——二维平面——三维空间的逐步学习过程，形成一种具备直观感受下的空间思考能力.

直观想象素养分为三个水平层次，其一是直面感官想象的能力；其二是形成数形结合的思想；其三是构建直观模型的体系.课程标准明确指出，我们教学需要适配的三个方向，即认识、形成、构建！本文结合2020年浙江省高考立体几何解答题，从直观想象三个水平层次的角度，谈一谈如何在教学中培养学生的直观想象能力.

题目(2020年浙江卷第19题)如图1，三棱台DEF-ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC=2BC.

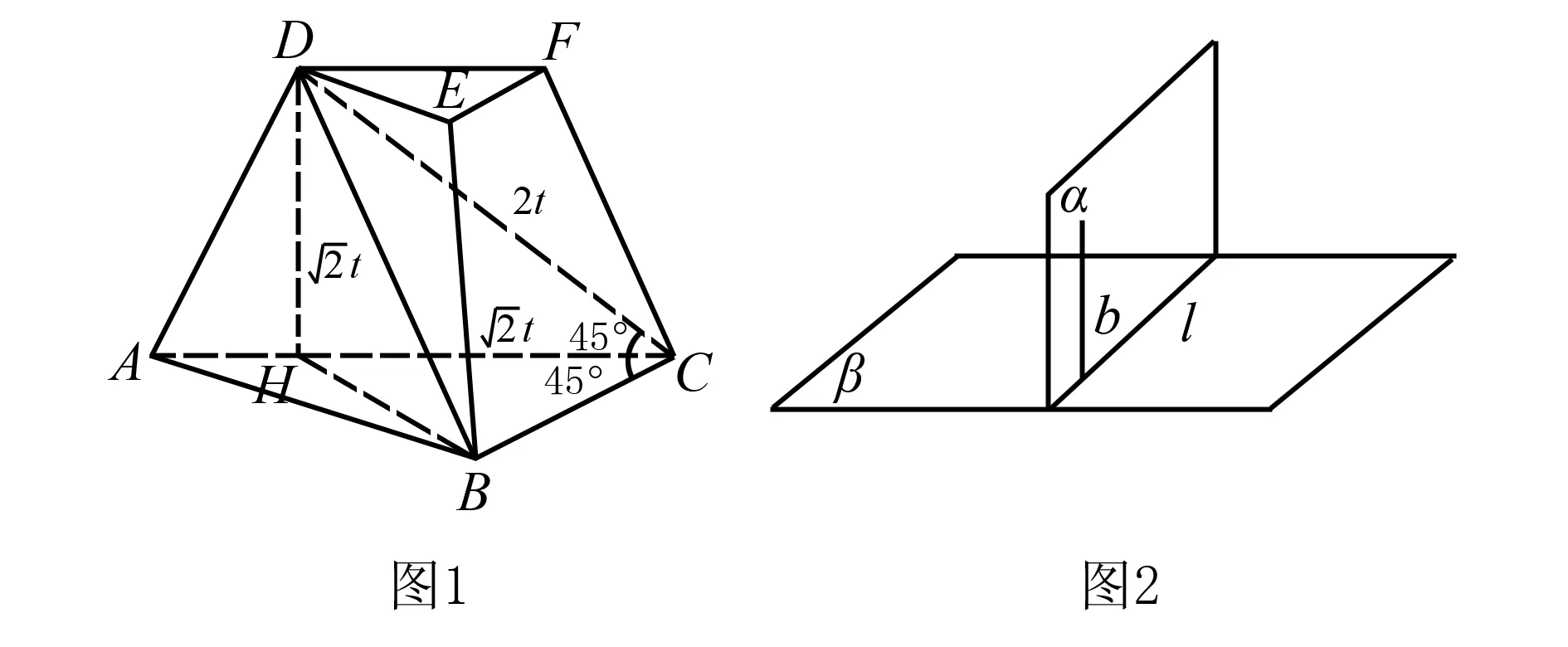
(1)证明：EF⊥DB；

(2)求DF与面DBC所成角的正弦值.

层次一：兴于形——直面感官想象的能力

立体几何解答题往往已经给出图形，这就在水平层次一上.读懂几何试题的一般图形，是最直接的感官想象能力.具体分析一下，第(1)问考查的是异面直线垂直问题，是一个常规问题，这类问题的基本策略就是借助线面垂直证明线线垂直．此处可直接利用平面与平面垂直的性质定理(如图2)：两个平面(α和β)垂直，则一个平面垂直于交线(l)的直线(b⊂α，b⊥l)与另一个平面垂直(b⊥β)．

层次二：立于思——形成数形结合的思想

空间几何本身就是以图形为载体，通过传统欧式几何定理，利用“形”的视角解决问题，也可以从“数”的视角，利用向量运算解决问题.纵观近年来浙江高考立体几何解答题，我们不难发现，命题组一直努力在寻求两种方式的平衡，即不能让“代数运算”的向量方式占据绝对优势，因此命题组在传统欧式几何方式和建系向量方式上努力寻求平衡点.这一命题思路，正是暗示了我们的一线教学，需要从两个方面指导学生立体几何的学习，“形解”和“数解”都要掌握，因此笔者提出，立体几何教学要两法并举、齐头并进，切勿“单腿走路”.现在一线教学对于传统欧式定理的教学往往有所放松，而中学数学更注重“形”的培养，以形辅数在数形结合思想中占据着更为重要的地位，来看“形”解：

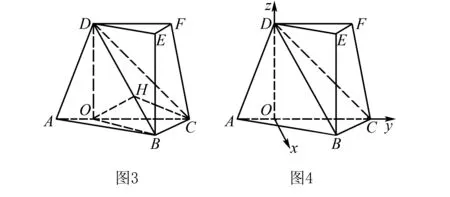
解析(1)如图3，过点D作DO⊥AC于点O，连接OB.

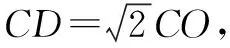
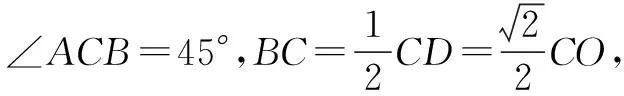
所以BC⊥平面BDO，故BC⊥DB.

由三棱台ABC-DEF得BC∥EF，所以EF⊥DB.

(2)过点O作OH⊥BD于点H，连接CH.

由三棱台ABC-DEF得DF∥CO，所以直线DF与平面DBC所成角等于直线CO与平面DBC所成角.

由BC⊥平面BDO，得OH⊥BC，故OH⊥平面BCD.

所以∠OCH为直线CO与平面DBC所成角.

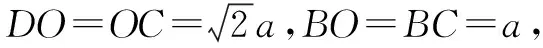
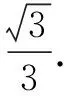
层次三：成于新——构建直观模型的体系

随着学生掌握知识的进步，我们发现愈来愈多的学生会利用空间向量的方式解决立体几何问题，这也是方法的进步.记得浙江大学金蒙伟教授说过：我们一直想努力命一道传统欧式几何法不吃亏、空间向量不占便宜的立体几何试题，但是真的很难，就好比是有了计算器之后，无论如何使用算盘都占不到便宜！在教学中，如何快速引导学生建构直观模型，是空间几何学习的必备方向.

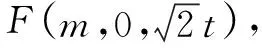
解析由三棱台ABC-DEF得DF∥CO，所以直线DF与平面DBC所成角等于直线CO与平面DBC所成角，记为θ，如图4，以O为原点，分别以射线OC，OD为y，z轴的正半轴，建立空间直角坐标系O-xyz.

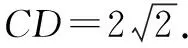
设平面BCD的法向量n=(x,y,z).

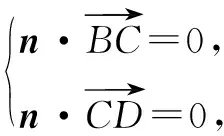
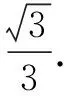
“数”解方式——空间向量法在计算中设而不求的思想在解析几何中常见，在立体几何中不常见，对学生是否敢于尝试带参数求解是一个考验．笔者尝试将这个题目给高二学生去做，竟然有了一个“惊人”的发现，出现了两种不按常理出牌的思路，通过对这两位学生的了解发现，他们能准确地发现此题的结果和点E，F的位置无关，仅和两个45°有关．

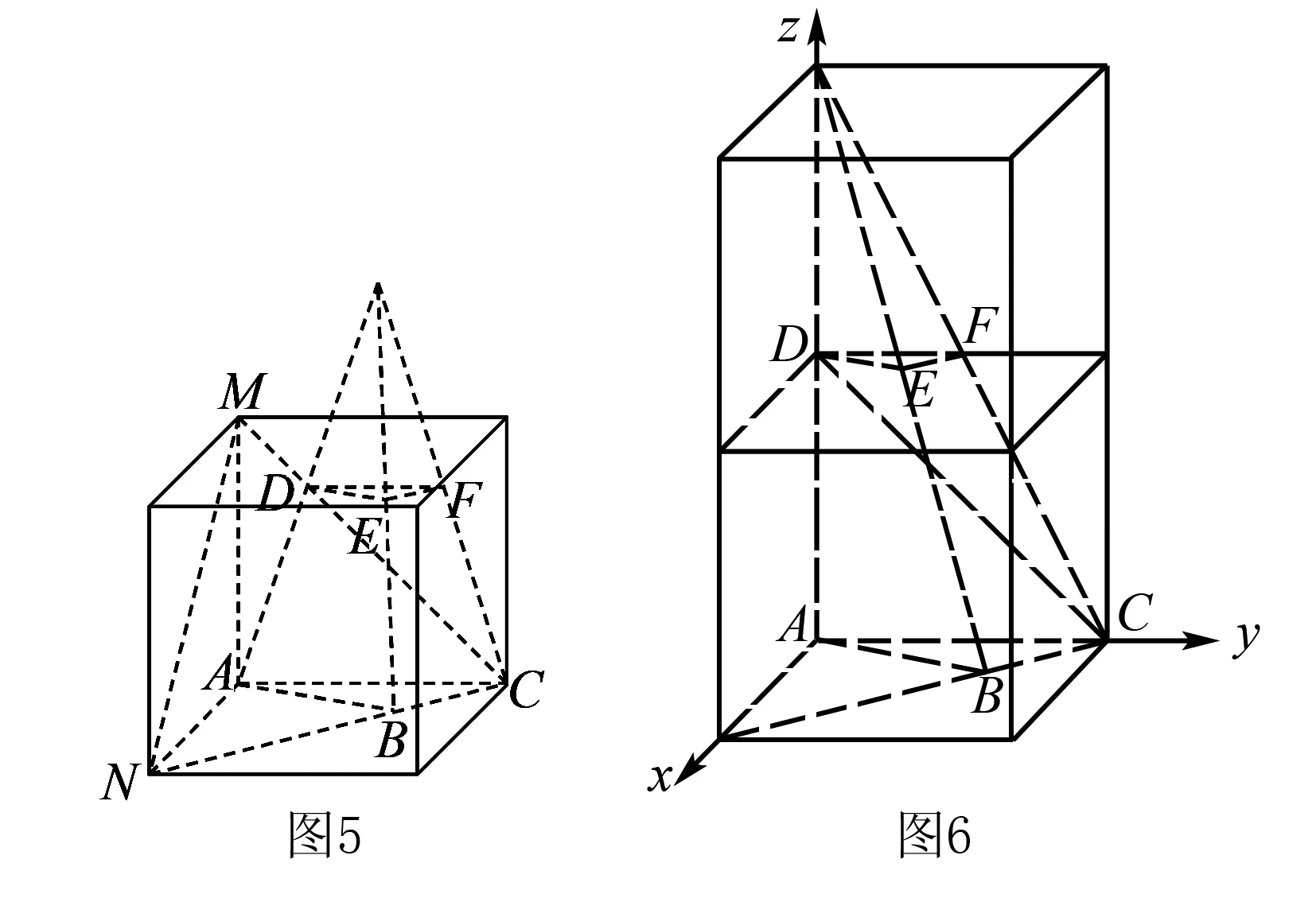
第一种思想是将这个台体图形内置到一个正方体内，问题就变成了正方体的棱AC和面CMN所成角的问题(如图5所示)，这也是此题可以设而不求的几何背景．

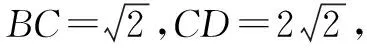
抛开这两种解题过程，笔者发现，提供这两种解法的学生都是数学实验社团成员，并且都是参与数学实验活动积极性很高的学员.在解题过程中联系平时的数学实验经验，提出“猜想”，笔者认为这就是“直观想象”的一种体现.

因此，于教师而言：作为数学科重要的核心素养直观想象而言，笔者从课程标准的三个水平层次进行了与一线教学落地的对比解读．而将核心素养进行落地，是需要一线教师在认真研学课程标准的基础上，融入自身教学的思考．

于教学而言：

兴于形——初等数学要注重几何图形的掌握；

立于思——问题解决要关注数形结合的魅力；

成于新——类比学习要寻求思维创新的突破.

因此直观想象素养恰恰是要求我们将这种启发、引导、创新带给学生，从而提高学生直观想象能力和思维的含量，获得更好的学习效果和学习体验，是为直观想象素养三个水平层次．