抛物线焦点弦的性质结论归纳与应用

韩义成

(甘肃省积石山县积石中学 731700)

我们在平时的学习中善于归纳总结一些数学的性质和结论，就能提高解题的效率和速度，做到事半功倍的效果.下面是我在教学中归纳总结的抛物线焦点弦问题的性质和结论，供参考.

若AB是抛物线y2=2px(p>0)的焦点弦(过焦点的弦)，且A(x1,y1)，B(x2,y2).

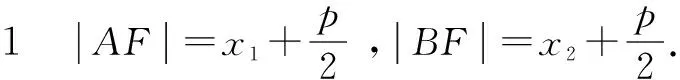
结论2|AB|=x1+x2+P.

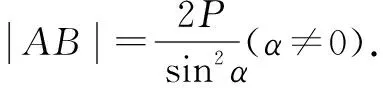
(2)焦点弦中通径(过焦点且垂直于抛物线对称轴的弦)最短.

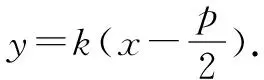
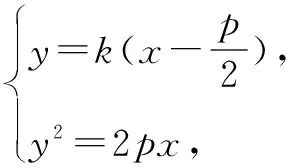
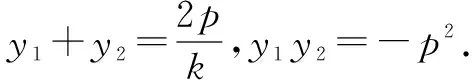
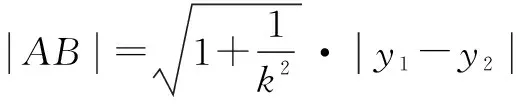
易验证，结论对斜率不存在时也成立.

(2)由(1)知，当AB为通径时，α=90°，sin2α的值最大，|AB|最小.

例1 已知过抛物线y2=9x的焦点的弦AB长为12，则直线AB倾斜角为____.

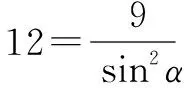
结论4两个相切：(1)以抛物线焦点弦为直径的圆与准线相切.

(2)过抛物线焦点弦的两端点向准线作垂线，以两垂足为直径端点的圆与焦点弦相切.

已知:AB是抛物线y2=2px(p>0)的过焦点F的弦，求证：(1)以AB为直径的圆与抛物线的准线相切.

(2)分别过点A、B作准线的垂线，垂足为点M、N，求证：以MN为直径的圆与直线AB相切.

证明(1)设AB的中点为Q,过点A、Q、B向准线l作垂线，垂足分别为点M、P、N，连接AP、BP.

由抛物线定义，知|AM|=|AF|.

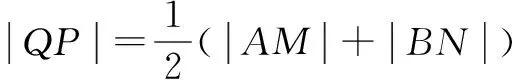
所以以AB为直径的圆与准线l相切.

(2)如图2，取MN中点P，连接PF、MF、NF.

因为|AM|=|AF|，AM∥OF，

所以∠AMF=∠AFM，∠AMF=∠MFO.

所以∠AFM=∠MFO.同理，∠BFN=∠NFO.

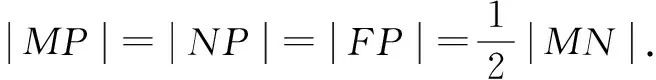
所以∠PFM=∠FMP.

所以∠AFP=∠AFM+∠PFM=∠FMA+∠FMP=∠PMA=90°.

所以FP⊥AB.

所以以MN为直径的圆与焦点弦AB相切.

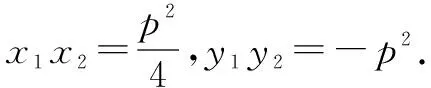
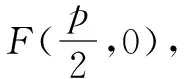
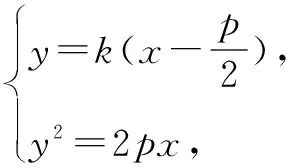
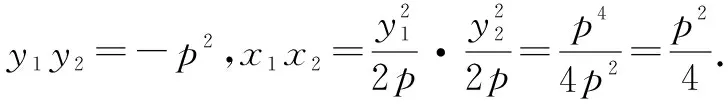
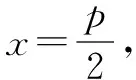
则y1=p，y2=-p.

所以y1y2=-p2.

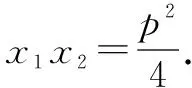
例2 设抛物线y2=2px(p>0)的焦点为F，经过点F的直线交抛物线于A、B两点．点C在抛物线的准线上，且BC∥x轴．证明:直线AC经过原点O．

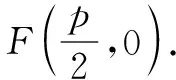
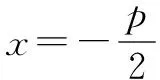
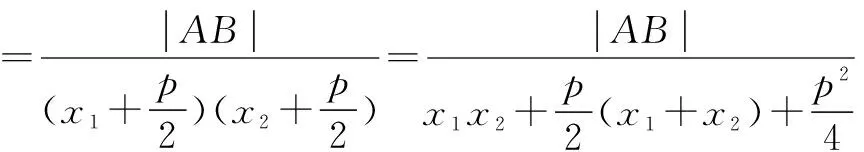
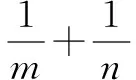
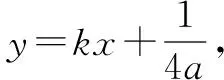
4a2x2-4akx-1=0.

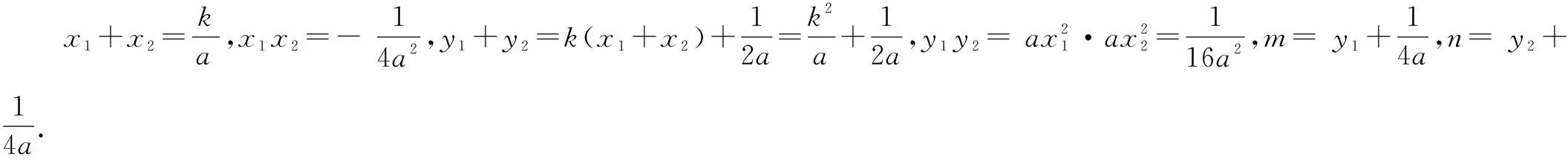
解法2特值法.当直线平行于x轴时得出答案.

解法3利用定比分点坐标公式.

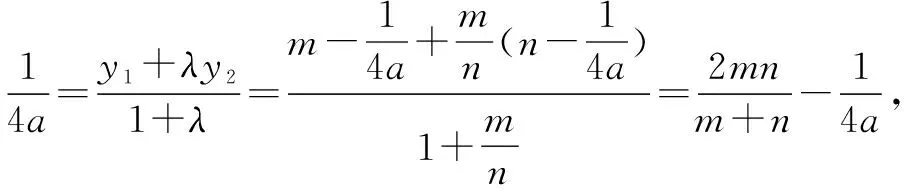
结论7过抛物线y2=2px(p>0)的焦点F作一直线交抛物线于A(x1,y1)、B(x2,y2)两点，过A、B两点分别作抛物线的切线，设其交点为M．则

(1)点M在抛物线的准线上;

(2)FM⊥AB;

(3)AM⊥BM.

逆命题过抛物线的准线上一点M作抛物线y2=2px(p>0)的切线,切点分别为A、B,则直线AB过焦点F．

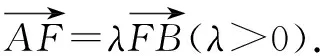
(2)设△ABM的面积为S，写出S=f(λ)的表达式，并求S的最小值．

解析(1)由已知条件，得F(0，1)，λ>0．

设A(x1，y1)，B(x2，y2)．

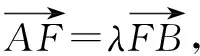
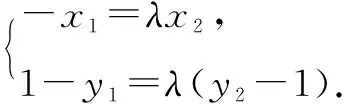
①

②

y1=λ2y2.

③

所以过抛物线上A、B两点的切线方程分别是

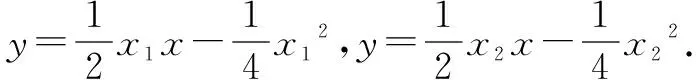
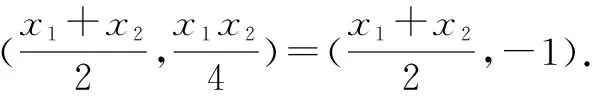
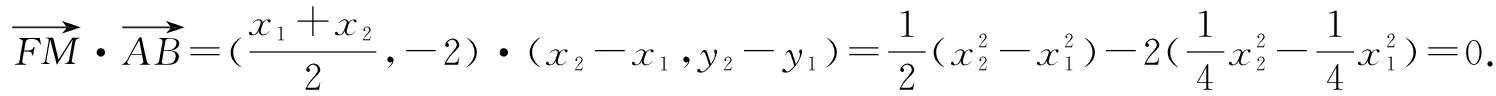
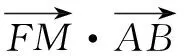
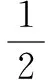
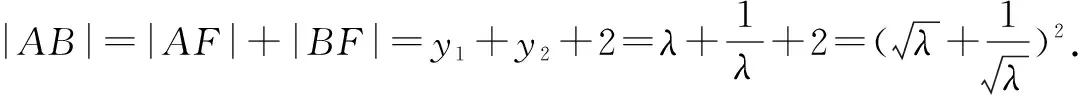
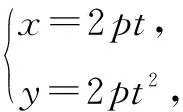
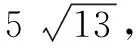
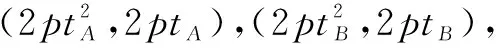
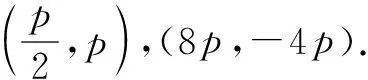
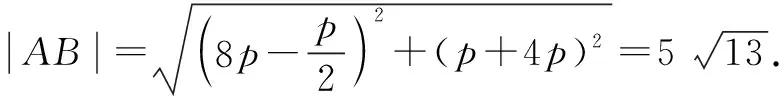
解得p=2．

总之，只要我们在平时的教学中善于归纳、总结、整理，就会得出一些课本之外的性质和结论，对我们的学习、解题有很大的帮助.