深部地质钻探孔内钻杆动力响应特性研究

瞿 坤

(陕西铁道工程勘察有限公司，陕西 西安 710043)

0 引言

与浅层地质钻探不同，深部地质钻探时，钻杆的长细比很大，刚度小，钻孔与钻杆间距小，钻速快，穿越地层众多[1-2]，因此，钻进时引起钻杆的剧烈振动，其动力学响应特征复杂[3-5]，其振动形态包括纵振、横振、扭振、涡动等多种振动形式[6]，这些振动形式的叠加及引发的杆件共振，极易导致钻杆的应力集中，给钻探造成施工风险和设备损耗。1991年，前苏联科学家Mizajanzade[7]对钻杆的动力学特征进行了初步的探索并给出了相应的研究成果；随后Finnie、Bailey、Paslay等人[8-10]对仅考虑纵振、横振和扭转振动一种振动形式的动力学模型进行分析和求解，其结果与实际成果相差较大；朱才朝等[11]认为钻杆的振动属于非线性振动，采用能量法建立考虑横向、纵向和扭转振动耦合的动力学模型，并对其进行数值分析；李国庆等[12]分析钻杆振动的模态，考虑钻杆的纵振、横振及扭转振动之间的耦合关系，但由于模型考虑了横向振动，加大了模型的复杂度和计算的难度。

本文尝试建立仅考虑纵向振动和扭转振动耦合作用下的深部地质钻杆动力学分析模型，并推导振动振幅与振动频率公式，在此基础上，使用有限元分析软件ANSYS直接建立深部地质钻探的钻杆有限元仿真模型，研究其频率变化规律并预测其动力学响应特征，从而科学合理地指导地质钻探。

1 仅考虑纵向和扭转的钻杆动力学方程

由图1可见，建立钻杆动力学离散分析模型，图中U表示钻杆的纵向位移，φ为钻头的转动角位移。

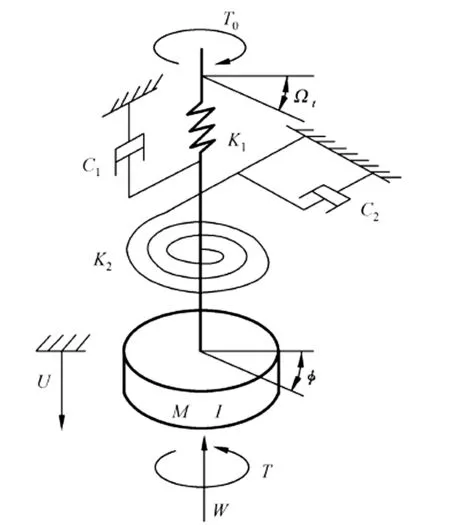
图1 钻杆系统动力学离散分析模型示意图Fig.1 Diagram of discrete dynamics model of rod system

钻杆系统的动力学方程可以表达为[13-14]：

(1)

式中：M为钻具质量，I为转动惯量，K1为钻杆纵向刚度，K2为钻杆扭转刚度，Ω为钻速，C1为纵向阻尼系数，C2为扭转阻尼系数。T0为扭矩，W为钻杆纵向压力，可以分别用如下公式表示。

W=Kc·(U-s)

(2)

(3)

s=s0sin(Φ)

(4)

(5)

式中：R为钻头半径，Kc为接触刚度，μ为摩擦系数，s为削切深度。

将公式(2)～(5)代入公式(1)，可以表达为

(6)

(7)

(8)

式中：

(9)

设

(10)

其中：a1、a2、θ1、θ2满足以下方程

(11)

整理得：

(12)

(13)

可计算得钻杆的振动频率为

(14)

2 深部地质钻杆仿真模型的建立

深部地质钻孔钻进时，钻杆的力学行为特征十分复杂，为简化计算模型和观测其动力学特征，对钻杆系统进行一定的理想化假设：

1)不考虑钻杆的弯曲，钻进时，钻杆的中心轴线与钻孔的中心轴线重合，钻孔为绝对垂直孔，重力方向沿钻孔轴线垂直向下，同时，钻杆和钻孔的截面均为规则圆形。

2)不考虑钻杆接头和其他构件的影响，将钻杆整体简化为一根筒状圆柱体，且材质均匀；钻头和岩心管与钻杆保持相同的材料特性和尺寸、物性参数。

3)忽略泥浆液体对钻杆的浮力和钻孔侧壁对钻杆的摩擦力。

计算时，钻杆的尺寸为外径89 mm，内径78 mm，钻头和岩心管的外径为95 mm，内径为78 mm。模型中钻杆的物理力学参数见表1。

表1 钻杆模型计算物理力学参数Table 1 Physical and mechanical parameters of drilling rod model

深部地质钻探一般采用正循环回转钻进，泥浆液护壁，悬浮钻渣，钻杆在钻进过程中，主要承受钻机传递的竖向轴力和旋转扭矩、钻杆本身自重和泥浆液体的浮力、钻头的钻进阻力以及阻力扭矩、钻杆与孔壁的摩阻力。为了分析的可行性和实用性，对模型的边界条件进行定义。首先，钻杆顶部受到钻架与钻机约束，在深部钻进时，钻进进尺缓慢，单位时间内的轴向位移可以忽略不计，因此采用固定边界条件；其次，钻杆的底部边界条件约束相对较少，岩心管与钻头受到岩土层的径向约束，在径向方向上的位移可以忽略不计，而在轴向方向的位移自由，因此，对钻杆底部采用不约束轴向位移的边界条件。

模拟采用商用ANSYS软件分析钻杆的纵向振动、横向振动与扭转振动，建立钻杆系统长度为300 m，钻具公称直径为95mm，研究钻杆的动态响应特征。根据《地质岩心钻探规程》(DZ/T 0227-2010)可知，深部地质钻探时，95 mm规格钻机的钻探参数为，最大钻压为20kN，正常钻压范围为12～15 kN，钻速范围为350～700 r/min，因此考虑到实际一般情况，选取钻杆施加轴向荷载为15 kN，钻速350 r/min，钻探中通用YDX-2型钻机的扭矩范围为600～5800 N·m，计算时扭矩取为600 N·m。建立的钻杆系统模型见图2。

图2 钻杆系统仿真模型Fig.2 Simulation model of drilling rod system

3 深部地质钻杆振动仿真结果分析

3.1 深部地质钻杆模态结果分析

利用ANSYS 求解器可以计算出钻杆纵向振动、扭转振动前10阶模态的固有频率w见表2。

表2 钻杆前10阶模态固有频率计算结果Table 2 The natural frequency calculation results of the first 10 modes of drilling rod

为便于阐述方便，选取前3阶模态进行分析，图3为钻杆纵向振动轴向位移云图，从图3中可以看出在1阶模态下，沿钻杆轴线方向上，钻杆顶部出现极小值，位移为0，钻杆底部出现极大值，位移为0.010 862 m；在2阶模态下，极小值向钻杆中部移动，距离钻杆顶部约100，位移为-0.001 08 m，极大值仍出现在钻杆底部；在3阶模态下，轴向位移出现3个极值点，极大值(0.010 859 m)分别出现在钻杆顶部和钻杆底部，极小值出现在极大值之间，距离钻杆顶部180 m，位移约-0.010 846 m。将3个模态的轴向位移与深度的曲线关系绘制成图4，由图4可见，随着模态阶数的增加，钻杆的轴向位移变化越来越剧烈。

图3 不同模态下钻杆轴向振动计算位移云图Fig.3 Calculation displacement cloud diagram of axial vibration of drilling rod under different modes

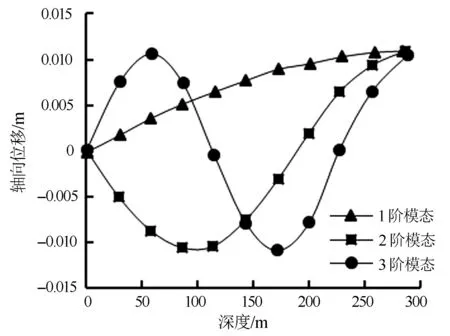
图4 钻杆轴向位移与深度关系Fig.4 Relationship between axial displacement and depth of drilling rod

图5为不同深度条件下，钻杆固有频率随着模态阶数的变化关系。由图5可见，无论是何种深度条件下，随着模态阶数的增加，固有频率呈现线性增加；在相同模态阶数条件下，随着深度的增加，固有频率逐渐降低，但降幅逐渐减小。

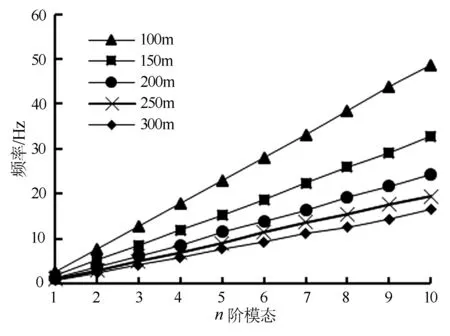
图5 不同模态下钻杆频率变化关系曲线Fig.5 Relationship curve of drilling rod frequency variation under different modes

钻杆的扭转振动与纵向振动具有类似的规律，具体见图6～图8。

图6 不同模态下钻杆扭转振动计算角位移云图Fig.6 Angular displacement diagram for torsional vibration calculation of drilling rod under different modes

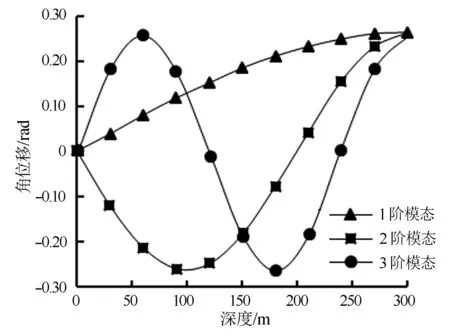
图7 钻杆扭转角位移与深度关系Fig.7 Relationship between angular displacement of torsional vibration and depth of drilling rod

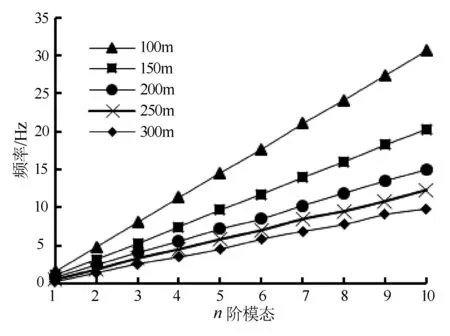
图8 不同模态下钻杆频率变化关系曲线Fig.8 Relationship curve of drilling rod frequency variation under different modes

3.2 深部地质钻杆位移-频率响应特征分析

钻杆在持续的周期载荷作用下会产生持续的动力响应，为避免深部钻杆在谐振动作用下，发生失稳破坏，有必要对钻杆谐振动响应进行分析，研究其频率变化规律并预测其动力学响应特征，从而科学合理地指导地质钻探。

通过ANSYS软件时间历程后处理模块抽取深度48 m、190 m、300 m处轴向位移对频率的响应分析(图9)。由图9可见，当激振频率接近钻杆1阶固有频率时，整个钻杆的轴向位移对激振力的响应比较明显，振动频率主要集中在低频段，数值小于2 Hz。在深度48 m处，轴向位移远小于190 m、300 m深度处的位移，而190 m与300 m深度处的位移较为接近，表明钻进时，钻杆的下部发生较为激烈的跳动，且发生位置不仅仅限制在钻头和岩心管附近。

图9 钻杆轴向位移对纵向振动频率的响应特征Fig.9 Response of axial displacement of drilling rod to longitudinal vibration frequency

图10为不同深度钻杆角位移对纵向振动频率的响应曲线。由图10可见，当各阶激振频率接近固有振动频率时，钻杆的角位移出现极值，钻杆的角位移在不同的振动频段出现谐波阻尼减小，其他频段的共振现象不明显。当激振频率接近钻柱扭转2阶固有频率时，整个钻杆的角位移对激振力的响应比较明显，引起的扭转振幅较大。频率小于2 Hz时，在深度190 m处，角位移远小于48 m、300 m深度处的角位移，而48 m与300 m深度处的角位移较为接近，表明钻杆顶段、底段的扭转相对中段较为严重。

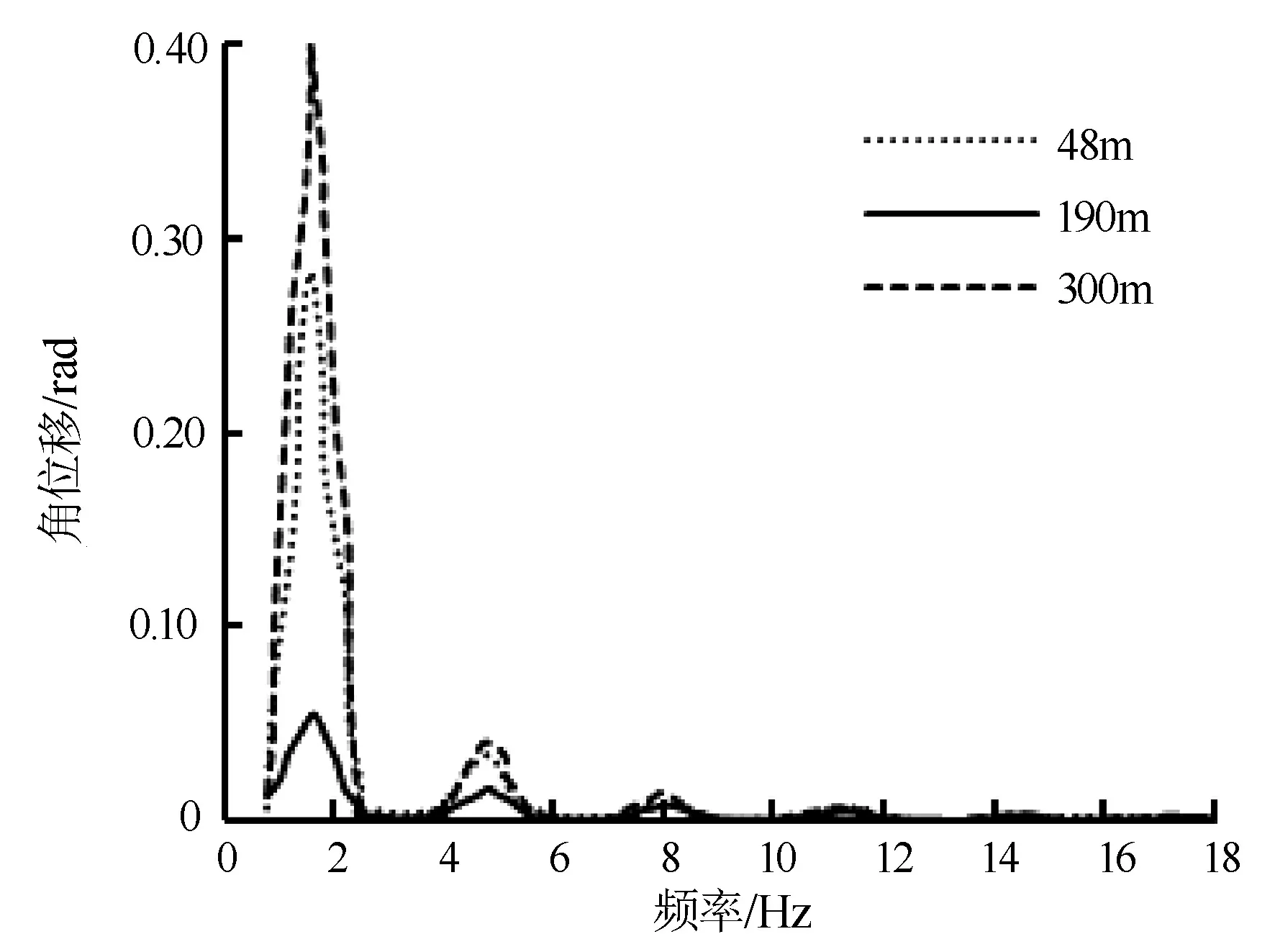
图10 钻杆角位移对纵向振动频率的响应特征Fig.10 Response of angular displacement of drilling rod to longitudinal vibration frequency

4 结论

针对深部地质钻探时，钻杆的振动形式多样，动力学响应特征复杂。本文建立仅考虑纵向振动和扭转振动耦合作用下的深部地质钻杆动力学分析模型，在理论推导的基础上采用有限元分析方法，得出以下几个主要结论：

1)在不同的振动形式下，随着模态阶数的增加，钻杆的振动位移变化越来越剧烈和越复杂。

2)随着模态阶数的增加，钻杆在不同振动形式下的固有频率呈现线性增加；在相同模态阶数条件下，随着深度的增加，固有频率逐渐降低，但其降幅逐渐减小。

3)当激振频率与钻柱纵向(扭转)振动固有频率相近时，钻杆的轴向(角)位移达到极值。钻杆轴向位移对正弦激振频率接近1阶纵振固有频率时，其动力响应特征明显，而钻杆的角位移在正弦激振频率接近2阶扭振固有频率时，其动力响应特征明显。